Непараметрическое моделирование интеллектуальных систем при неполной информации

НЕПАРАМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ ИНТЕЛЛЕКТУАЛЬНЫХ СИСТЕМ ПРИ НЕПОЛНОЙ ИНФОРМАЦИИ

Приведена схема управления многосвязным технологическим процессом. Даны общая и математическая постановки задачи управления многосвязным процессом. Построены непараметрические модели идентификации входных и выходных значений управляемого процесса.

При моделировании и управлении сложными технологическими процессами часто возникает ситуация, когда параметрическая зависимость по ряду каналов объекта неизвестна полностью или частично. В этой связи перспективным является использование теории непараметрических обучающихся систем [1]. Рассмотрим формулировку задачи идентификации и управления для одного объекта, который будем считать фрагментом технологического процесса.

Общая постановка задачи. Рассмотрим схему (рис. 1).

Рис. 1. Схема управления процессом: О-объект;

АС - адаптивная система; ut - управляющее воздействие;

- контролируемое неуправляемое воздействие;

^ _t - случайное воздействие; х,, z_t - выходные переменные; h^u, h " , h^x, h^z - помехи в каналах измерения; u_t^h, ц ? , x_t^h, zj -измеренные значения соответствующих переменных;

xj и zj- заданные значения выходных переменных

Следует заметить, что блок АС представляет собой достаточно сложную структуру, детализацию которой приводить не будем, лишь укажем, что в ее состав входят как модель исследуемого процесса, так и соответствующая процессу иерархия блоков управления.

Целью системы управления является поддержание заданного значения х* и z*. Отметим в связи с этим суще ственные отличия выходных переменныхxt и z. Выходная переменная х контролируется через достаточно малые интервалы времени At, как и переменные u, ц, А выходная переменная z отслеживается через существенно большие интервалы времени AT (AT>> At). С технологической точки зрения для всего технологического процесса наиболее важным является контроль именно этой переменной. Например, если выходная переменная х контролируется с помощью различного рода индукционных, емкостных и других датчиков, то выходная переменная z - по результатам химического анализа, физико-математических испытаний и др. Этим и обусловлено существенное отличие дискретности контроля выходных переменных х, и z. Если дискретность измерения х u ц. - это секунды, минуты, то дискретность z, составляет смену, сутки, недели и более. Последнее обусловлено технологией проведения самого контроля, который обычно регламентируется государственным стандартом.

Математическая постановка задачи. Пусть Ц , = { ц¹„...,ц k } е R k , u , = { u t ,..., u m } е R m , x , = { x 1 ,..., x , } e R " , z , = { z , ¹ ,..., z , } s R l . Характеристики объектов О₁, О₂и О₃ взаимооднозначны по вектору управляющих переменных, т. е. одному значению u_tсоответствует только одно значение y._t. Имеется обучающая выборка { ц _t , u,, х, Z_t _ ф, t = 1, 5 }, где т указывает на запаздывание (смена, сутки ит.д.).

Сформулируем критерий оптимальности:

R ( z ) = M_u , ц { M z ( z _ z )² | u , ц} = m i n,         ⁽¹⁾

где zt - оценка вектора выхода z.

Используя необходимое условие минимума, т. е. приравняв производную функции R по искомой величине z к нулю, получим:

z^opt = M ( z\u , ц}.                     (2)

Непараметрическая оценка выходной переменной zt для системы (см. рис. 1) имеет вид

s

m

k z s + 1

Z z. П ф i = 1        j = 1

u s V

^^^^^^в

j

U , 1

n

П ф

Ц ^р + 1

^^^^^^в

Ц p

sm

ZПФ

fu j u s + 1

^^^^^^в

us

j

ui

n

П ф

I p

^Ц s +1

^^^^^^в

Ц y i c²

⁷ , (3)

где s - размер обучающей выборки; z ” _{s +1}'

k

^^^^^^в

7

оценка к-й

компоненты вектора выхода, к = 1, l ; и$+1- вектор входа из экзаменующей выборки; Ф - ядро функции, и выбираемое по следующим условиям: j Ф(b)db = 1;

ОО г                 ^ви

Ф( b₁ ) <Ф ( b ₂ ) для | b₂ | < | b | ; j b^p Ф ( b ) db <^ ,р = 2,3,...;

вИ

Ъ - аргумент функции Ф ; С_й - параметр размытости ядра Ф, удовлетворяющий условиям: C n ^»_0 ; «с „ ( n ) n - >_~ .

При выполнении этих условий оценка z является асимптотически несмещенной, состоятельной, асимптотически нормально распределенной.

Параметр размытости С выбирается по условию выполнения минимума критерия:

Пусть N, О ,A - размерности векторов z_t¹, z_t² и z_t³; N, О , A - размерности векторов z_t¹, z_t² и z_t³; H, F и T - размерности векторов x_t¹, x_t², x_t³; У , Г и Q - размерности векторов и ¹, и ² и и ³; D - размерность вектора ц _t .

Запишем модели прогноза выходных значенииzt1,zt2, zt3 и xt1,xt2, xt3, а также модели расчета управляющих воздействий ut1, иt2, иt3 для объектов О1, О2 и О3.

Непараметрические оценки выходных переменных zt1, zt2, zt3 будут выглядеть следующим образом:

1 18 __ z s +ф =

а 25

z s +ф =

s

у

Z z 1 П ф i = 1        j = 1

й;+1в u,

u ¹ s

D

Ц k + 1

в

Цк

Ц s

s У

ZПФ

Us+1 в U,

D

П ф

Ц k + 1

в

Ц k

,

u ¹ s

5 = 1, N ,

Ц s

(9),

s Г

Z z25 Пф i=1        j=1

u

в й ² i

N

1k zs +ф в

z ¹ i^k

u ² s

s

R = Z ^{( z}i ^{в z}i⁽ C ^{)) 2 —} min, i = 1                               C

s Г

ZП Ф i =1 j =1

^u s +1 ^{в u} i

N

с к ^zs

1k1k zs+ф в zi

Н

Пф i=1

1 p x +

^^^^^е

x ¹ i^p

u ² s

с к

^{V zs}

Н

Пф p=1

A___

1 p x s +1

C p ₁ xs

^^^^^в

x 1 _ip

,

X

C p ₁ xs

где s - размер обучающей выборки.

Критерий оптимальности для оценки управляющего воздействия выглядит так:

отсюда R ( й) = M _Ц z _x { M u ( u - й ) ² | ц, z , x } = min, (6),

^Ц ’ ’                                                             й

5 = 1, О ,

(Ю)

отсюда й °^р t = M ( u | ц, z , x = z * }.

~35 _ z s + ф =

sQ

Z z3 Пф i=1        j=1

u

^^^^^в

u3ij

u ³ s

О

z

/2 к

Формула оценкиу-го компонента вектора и в момент времени s+1 записывается следующим образом:

sQ

ZП Ф i =1 j =1

^u s + 1 ^{в u} i

О

_

”2 к

■ s +ф ^{в z}

Ck z2s

, 2 к ^

F

- П Ф

2p x +

^^^^^в

2 p x L

u ³ s

z-CCPV z s

, 2 к ^

.z

F

p =1

p =1

j u s +

где j = 1, m .

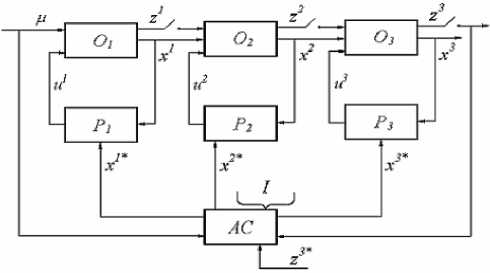
Непараметрические модели последовательного технологического процесса. Приведем сравнительно простую схему технологического процесса (рис. 2). На это схеме опущены помехи, действующие в каналах измерения, чтобы не загромождать рисунок, хотя предполагается, что они, конечно же, действуют.

35 _ x s +1 =

£ 25 _ x s +1 =

Рис. 2. Схема последовательного технологического процесса (обозначения см. в тексте)

Содержание переменных соответствует описанному ранее. Отметим лишь, что роль неуправляемых переменных в данной схеме играют как ц t , так и z¹, z², контроль которых, производится через различные, но значительные интервалы времени. Блоки Р₁, Р₂ и Р₃ - это регуляторы соответствующих объектов О_р О₂ и О₃; I- вся имеющаяся информация о процессе.

5 = 1, А .

C P A__ x A, 2 p 2 p x s +1 x i

C^p 2 xs

Непараметрические оценки выходных переменных x¹, x_t², xt³ записываются таким образом:

£¹⁵ x s + 1

s

Z x,²

i =1

s

у

Z x⁸ П ф i = 1        j = 1

й;+1в u,

u ¹ s

Г

D

Ц k + 1

в

Ц k

Цs

s у

s Г

ZП Ф i =1 j =1

u

u

в й i

u ¹ s

5 = 1, Н ,

в й ‘j

Н

u ² s

^й s +1 ^{в й} i

sQ

Z x - п ф i =1         j =1

u

Н

2 us

в

D

f x 1 к

.А___ x1sk

^^^^^в

k

C 1

в

C 1 V x s

5 = 1, F,

u ³ i^j

F

x ² s^k

Ц k + 1

1 k x _i

x1s x1ik

в

в

Ц k

Ц s

\N

Пф

Б=1

InПф p=1

x ² i^k

,

f _Z1 p ^z

.A_____

1p z s+1

X

^^^^^в

(12) zL '

C p ₁ zs

в

z 1 _ip

C p ₁ zs

,

sQ

ZП Ф i =1 j =1

^u s +1 ^{в u} i

F

u ³ s

C 2 x ^s_ f Y² к -Y² к ^x-c^ V         x ² s

5 = 1, T .

Lo_

Пф

2p z s+1

в

(13) z 2iL

О

Пф

X

CP

Л_____ z z

2p2p z s+1 z i

C p ₂ zs

,

Непараметрические оценки выходных переменных ut1, иt2, иt3 записываются следующим образом:

W¹⁵ u s + 1

s N

Z 4* Пф i=1       j=1

Z . - Z s + 1 i

D

^^^^^в

Ц

Пф

1 p *

x . . 1

^^^^^в

xl

z 1 s

Ц s

p = 1

s N i =1 j=1

jj z s+1 z i

D

в

Ц i

_z 1 _s

Ц s

Н

0 ^Ф

X f r1 p *

x s + 1

C^p x 1 s

в

x 1 _ip

,

c p

^{V xs 7}

5 = 1, Т ,                      (15)

* 25 u_S^ 1

s        П

Е и2 Пф i=1        j =1

ЕПф i=1 j =1

² j . _ . +1 z

z

Пф

z V^k * __v^{2 k} x s +1 x i

C \ x s

s +1

^^^^^™

. 2 j

z s

П ^ф

z 2k ^k * __v^{2 k} X s +1 x i

k

■ x2 s

\

z ^ ( и ) =

sk

Е z [ s ] П о i =1          j =1

( u j - u j [ i ] . C j [ s ]

n

П ^о

(^ C WT ^j

k

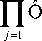
⁽ U j - U j [ i ] v C j [ s ]

П ^о

(

j

^{3 5} u s +1

sA

Е u35 Пф i=1       j=1

sA

ЕПф i=1 j=1

5 = 1, Г ,                       (16)

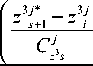
\t, о ф

₍ V³ k * _ V³ k x s +1    x i

\

k x3 s

^^^^^™

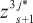
z s

в ^ф

( 3 k *      3 k x s+1 - x i

k x3 s

5 = 1, Q .

Непараметрические модели и алгоритмы управления с идентификатором. Рассмотрим задачу управления объектом с идентификатором в управляющем контуре (рис. 3). Как на предыдущей схеме (см. рис. 2), на этой схеме опущены помехи, действующие в каналах измерения.

На первом этапе, когда ключ К₁ разомкнут решается задача идентификации, на втором этапе, когда ключи К₁ и К₂, К₃, К₄ замкнуты, решается задача выработки управляющего воздействия, которое и подается на объект.

Далее для простоты записи будем рассматривать непараметрические алгоритмы на примере одного объекта. Для последовательной цепочки объектов алгоритмы записываются аналогичным образом.

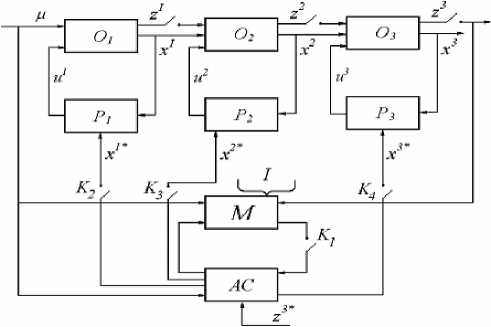
Рис. 3. Схема управления с идентификатором: модуль М - модель

Введем некоторую функцию качества ^о( t ⁾ = ^о( z ⁽ t ), z * ⁽ t )). Поскольку для показателя качества о( t ) , который представляет собой меру уклонения z(t) от z*(t), естественно потребовать равенство нулю, то оптимальное управляющее воздействие, в смысле квадратичного критерия о( t ) может быть представлено в виде условного математического ожидания:

u ( t ) = M { u ( t )/p( t ) e Q(p),o( t ) = OV z ( t ) e Q(z) } , (18)

Для решения задачи идентификации в условиях непараметрической неопределенности будем использовать непараметрическую модель идентификации объектов без памяти, алгоритм который имеет вид

⁷ , (19)

% = 1, m , где s - объем выборки; k, n и m - количество входных

управляемых, неуправляемых и выходных переменных

соответственно.

Задача сводится к непараметрическому оцениванию

(18) на основании поступающей информации { z_t , ц _t , u t } , t = 1, s . Ясно, что в качестве непарамет

рической оценки (18) может быть принята статистика

U (.^[ s ] = где

s - 1           k

Е u [ i ] П ⁰

i = 1           j = 1

s - 1 k

ЕПо i=1 j=1

⁽ О j [ s ]  C j [ s ]

⁽ о j [ s ] C [ s ]

V ^j

n

) П^О

П ^о

I j^

C j ^[ s ^]

z

^ i ^[ s ^{] v j}

+ A u j [ s ], (20)

O[ s ] = ( O 1 [ s ],..., о m [ s ] ) ; o j [ s ] = o j ( z j *[ s ], z j [ s ] ) ;

A u j [ s ] = A u ( o j [ s ] ) , j- количество входных управляемых

переменных; A u j [ s ] - изучающая добавка, j = 1, k .

Для того чтобы использовать опыт технолога-эксперта для выбора некоторых управляющих воздействий при решении этой задачи, алгоритм (20) следует модифицировать в форме

u j [ s ] =

f u [ i ] f о ⁽°™ 1 пт о ⁽ ^ j l s Di^' - о ^{( u} T ^{v s ] u} j ^[ i ^] 1:1   j    ¹ = ^П    I C j [ s ] 1 °! = ^П    I       C j [ s ]      J J j = 1   I       C j [ s ]

V ^k о ^{( о} j ^[ i ^] n о ⁽ ^ j ^{[ s ]} ^ j ^[ i ^] ” о ^{( u}j ^{[ s ] u}j ^[ i ^{] Е} J j = 1 I C j [ s ] JJ j = 1 I C j [ s ] IJ j = 1 I C j [ s ]

1, (21)

c <  k , j = 1, { k - c } .

В заключение приведем некоторые типы A u [ s ] адап

тивных непараметрических систем играющих основную роль при активном обучении:

- алгоритм с обратной связью

^{A u [} s ^] = е ( z * s , z s - 1 ) ,                   (22)

где е - некоторая функция, представляющая собой меру уклонения одного из элементов z s - 1 от заданного значенияz*;

- градиентный алгоритм

A u [ s ] = 0 s V x Q ( z * , z s - 1 ) ,                (²³)

где c _s - некоторая случайная последовательность; Q - выпуклая функция. Для этого класса могут быть ис

пользованы различные статистические оценки градиента, в том числе и непараметрические;

- обучающийся алгоритм. Для алгоритмов такого типа A w[s] определяется так

^{3 k} , z z, [ s ] - z ,[ i ] 1 .^T k T , z z, [ s ] - z ,[ i ] 1

^A u [ s ] = E ^A u [ s ] П О ^j C _s j^J / ЕП ^о    C I _s ]    (24)

j ^I i ⁷ i j ^I j ⁷

Приведенные непараметрические алгоритмы предполагают последовательную схему обучения и могут носить как активный, так и комбинированный характер.