Непараметрическое моделирование организационных систем

При разработке систем управления дискретнонепрерывными процессами часто возникает необходимость управления не отдельным технологическим объектом, а всем производственным комплексом. При этом представляется целесообразным рассматривать иерархическую схему управления промышленным комплексом. Разработка соответствующих обучающихся моделей и алгоритмов управления существенно определяется наличием априорной информации о технологических процессах, каналах измерения и, в сущности, предопределяет использование тех или иных разделов теории идентификации и управления. Основной акцент сделаем на наличии минимальной, как это представляется сегодня, априорной информации об исследуемых объектах, системах, т. е. будем рассматривать задачи идентификации и управления в условиях непараметрической неопределенности. В этом случае отсутствует этап определения модели или алгоритма управления с точностью до вектора параметров. Это обусловлено тем, что чаще всего информация, необходимая для предварительной параметризации или выбора параметрической структуры модели, недостаточная. Это делает подобный подход более реалистическим, чем общепринятая теория. Конечный существенный интерес представляет случай, когда некоторые объекты или каналы связи промышленного комплекса соответствуют одновременно как уровню параметрической неопределенности, так и уровню непараметрической. Это отдельная проблема, которая требует специального рассмотрения. Таким образом, настоящее исследование посвящено только случаю, когда априорной информации об исследуемой системе или процессе соответствует уровень непараметрической неопределенности. Отметим, что верхний иерархический уровень управления подобным комплексом представляет собой организационную систему управления с лицом, принимающим решения (ЛПР).

Моделирование дискретно-непрерывных процессов. Дадим краткую характеристику дискретнонепрерывного процесса, который является предметом исследования в традиционной задаче идентификации (рис. 1).

На рис. 1 введены следующие обозначения: А – оператор процесса; u ( t ) и µ( t ) – управляемые и неуправляемые входы процесса, соответственно; x ( t ) – выходная переменная процесса; x ˆ _t – выходная переменная модели; H ^µ, H^u и H^x – каналы измерения соответствующих переменных; h ^µ( t ), h^u ( t ) и h^x ( t ) – помехи, действующие в каналах измерения; µ _t , u_t и x_t – переменные процесса, измеренные в дискретные моменты времени (подразумевается, что они зашумлены соответствующей помехой h ). Следует также отметить, что и на сам процесс оказывает влияние некоторая помеха ξ( t ).

В дальнейшем исследуется дискретно-непрерывный процесс, представленный на рис. 2.

Здесь введена переменная выхода q ( t ), измеряемая через интервал времени ∆T >> ∆t , где ∆t – дискретность измерения переменных u ( t ), µ( t ), x ( t ). Чаще всего эти переменные измеряются электромагнитными средствами. Поэтому ∆t в технических системах достаточно мало. K – ключ, символизирующий канал контроля.

Обратим внимание на то, что ∆T может значительно превышать постоянную времени объекта, что приводит к необходимости рассматривать объект как статический с запаздыванием (рис. 3).

µ( t )

ξ( t )

>      Процесс

>       A

h ^µ

u ( t )

h u

u t

x(t) --------► hx

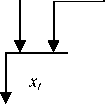
Рис. 1. Традиционная схема дискретно-непрерывного процесса

ξ( t )

µ( t )

q ( t )

h ^µ

u ( t )

hU

µ t

u t

Процесс A, B

x ( t )

hX

x t

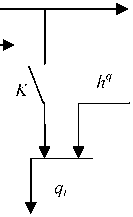
Рис. 2. Схема дискретно-непрерывного процесса при различной дискретности контроля

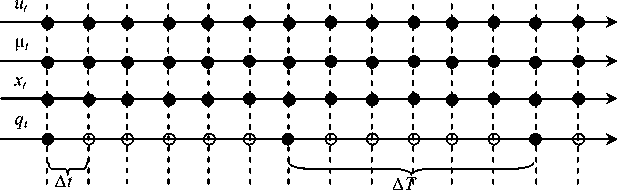
Рис. 3. Измерение переменных процесса производится с различной дискретностью ∆T>>∆t : • – моменты измерений по каждой из переменных; ○ – пропущенные значения

Процесс, представленный на рис. 1 и 2, описывается следующим образом:

д) lim C S *Ф ( u ) = 3 ( У — У, ) - свойство 5 -образно-

x ( t ) = A ( u ( t ) , ц ( t ) , ^ ( t ), t ) ,                   (1)

q ( t ) = в ( u ( t ) , ц ( t ) , ^ ( t ), t ) ,                   (2)

где A , B – оператор процесса – класс операторов, который определяется на основании имеющейся априорной информации. При существенном влиянии на x ( t ) случайных факторов ξ( t ), удовлетворительную

сти, а коэффициенты размытости C_S ядер эмпирической плотности вероятности зависят в общем случае от объема выборки S , причем C_S → 0 и sC_S → ∞ при s → ∞ , y – произвольный аргумент.

Непараметрическую модель процесса (2) можно

представить в следующем виде:

S

m

S ^Пф |

uv

—

uiv

l

ц v

—

ц v

n

xv

—

xiv

модель построить нельзя, даже при условии удачного выбора класса операторов B [1].

Непараметрическая модель процесса (1) может быть представлена как

( u , ц , x ) =

i = 1

C S

C S

C S

S

m

S№|

uv

—

ui

v

i

l

ц v

—

ц v

n

xv

—

xi

v

i

, (4)

x ( U , ц ) =

Sm

S x - П Ф i =1       v =1

u

v

—

u i ^v

C S

l

In Ф

v =1

Sm

sn ф

uv

—

u i ^v

i =1 v =1

C S

l

In Ф у v=1

CS

v = 1

CS

CS

ц v

—

ц v

C S

V      V

ц — Ц i

где ( u , ц , x ) - непараметрическая модель процесса q ( u , ц, x ), x e R ” , в которую включена выходная переменная x ( t ), измерения которой доступны через интервалы времени ∆t ; ядерная функция Φ( ∙ ) удовлетво-

C S

где x ( u , ц ) - непараметрическая оценка регрессии x ( u , ц); u e R m , ц e R m ; S - объем выборки; Ф( ■ ) - колоколообразная функция, или как ее еще называют ядерная функция; C – параметр размытости ядерной функции Φ(∙). Функция Φ(∙) обладает следующими свойствами:

• а)    0 ≤ Φ( u ) < A < ∞ ;

• б)    Φ( u ) = Φ(– u ); ю

• в)    | Ф( u) du = 1;

—ю

ряет показанным выше условиям.

Непараметрическое управление дискретнонепрерывными процессами. Управление процессом, представленным на рис. 1, осуществляется по схеме, представленной на рис. 4.

Обозначения на рис. 4 те же, что и выше, а x* – задающее воздействие. Непараметрический алгоритм управления при активном накоплении информации

имеет вид

k uS+1 =

Sn

S u , n Ф i =1      v =1

x

* ^v

S +1

—

C S

vl x-ln Ф у v =1

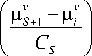
ю

г) J Ф ( u ) u m du < ю , при m > 0, u = y ——;

—ю ^x                                 C s

Sn sn Ф i =1 v =1

x

* ^v

S +1

—

C S

vl x" In Ф у v =1

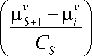
+ A u S +1 , (5)

где A u S ₊₁ - поисковые шаги, k = 1, m .

Управление УУ ^x (рис. 5) – устройство управления по выходной переменной x ( t ), УУ ^q – устройство управления по выходной переменной q ( t ), М 1 – макрообъект первого уровня, М 2 – макрообъект второго уровня. Роль управляемой переменной на этом уровне иерархии выполняет x* . Алгоритм управления на сле-

или оптимизаторами любой доступной информации о системе, требуемой для функционирования.

Общая постановка задачи имеет следующий вид:

дующем уровне иерархии имеет вид

x ˆ

k

S +1

Sw

SхПф i=1     v=1

q* S +i - q v

C S

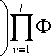
M{Q(q,z)}^ min.             (7)

q eQ ( q )

Ограничения в общем случае имеют вид:

m { v ( q , z ) } = 0, m M q , z ) } > 0.       (8)

Тогда непараметрический алгоритм оптимизации

Sw

ХП Ф

i =1 v =1

q* S +1 -

CS qiv

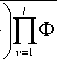
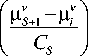
k

^{+ A} x S +1

, (6)

может быть представлен следующим образом:

где Ax * k _{+ 1} - поисковые шаги, k = 1, n ; q e R . Следует заметить, что на этом уровне иерархии предполагается наличие обучающей выборки с последующим ее пополнением в процессе функционирования замкнутой схемы. Дальнейшее обобщение системы управления сложным промышленным комплексом может быть представлено в виде схемы (рис. 6).

На рис. 6 СПР – система принятия решений с ЛПР; Q* ( q , z ) – заданная целевая функция, зависящая от q и от производственных показателей z , оказывающих существенное влияние на характер вырабатываемых воздействий СПР; отдельно выделена «Информация», указывающая на возможность получения блоком СПР

S

S q® s,.

k      -i=1*k q S+1     s + qi S+1

S ® s , . i =1

® s,i

w

=П Ф v=1

v q S+1

Cq'

V ^s

^{q v}

П ф

J ^v =1

z S +1

C s ^z

v

-Il ф P^v;^^ 111 sgn (*' ("-^‘J), v=1 V Cs      J v=1

где A q * k _{+ 1} - поисковые шаги, k = 1, w ; z e R ; функция sgn( y ) c произвольной переменной y следующая:

sgn (y ) =

1, если y >  0, 0, если y <  0.

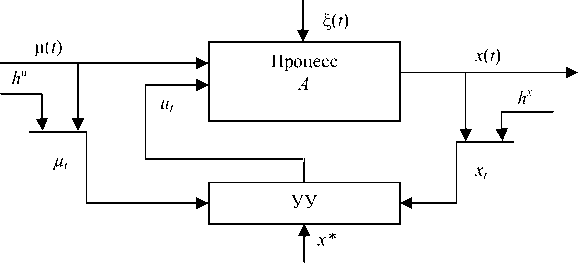
Рис. 4. Система управления комбинированным объектом

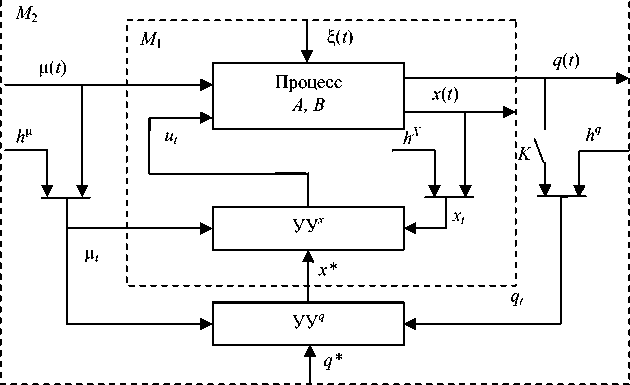
Рис. 5. Иерархическая система управления

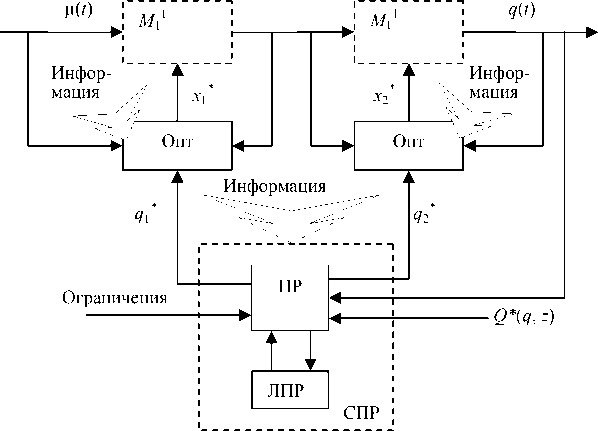
Рис. 6. Иерархическая система принятия решений с ЛПР

Параметр размытости C S – отдельная задача теории оптимизации. Вследствие трудности постановки экспериментов на реальном объекте в организационных системах, функция оптимизатора отводится человеку. ЛПР располагает областью определения параметра и, в зависимости от состояния системы, устанавливает то или иное значение, анализируя отклик организационной системы на выбранное значение параметра. В случае необходимости значение параметра изменяется, и вновь анализируется оклик. Область определения параметра C S , в свою очередь, обусловлена как естественными ограничениями, так и опытом и знаниями ЛПР в исследуемой области.

Обучающаяся система управления с идентификатором. Естественно считать, что первым этапом на пути создания подобной системы является построение модели (идентификатора). Причем требования к идентификатору достаточно высоки. Такая система, представленная на рис. 7, определена высокой степенью важности объекта (жизнеобеспечивающей и пр.), экспериментирование на котором крайне затруднено.

Поэтому в таких случаях используют не автоматические системы управления, а автоматизированные, т. е. системы с участием человека. В частности, сначала в диалоговом режиме вырабатывается управленческое решение с использованием идентификатора. Ключ K 1 разомкнут, ключи K 2 замкнуты. Конечно же, в этом случае идентификатор должен с достаточно высокой степенью точности описывать объект, включая внештатные ситуации или выход переменных процесса за пределы технологического регламента. После определения управляющего воздействия оно подается на исполнительный механизм (ключ K 1 замкнут).

Работа системы управления с идентификатором включает в себя следующие действия:

• –    ключ K 1 разомкнут, ключи K 2 замкнуты;

• –    выбирается некоторое заданное в рамках данной задачи значение выхода Q* ( x , z );

• –    значение Q* ( x , z ) подставляется в алгоритм расчета управляющего сигнала;

• –    полученное значение u ˆ ^l подается на идентификатор; отклик x ˆ _l идентификатора возвращается на управляющее устройство и подвергается анализу ЛПР;

• -    находится значение x * = x l +a ( C S , l ) , где a ( C S , l ) - убывающая по мере увеличения S функция; l – счетчик алгоритма;

• –    работа алгоритма продолжается с шага 2 до тех пор, пока не будет найдено некоторое значение * l

• u    = u , удовлетворяющее цели управления;

• –    после того как u* найдено, ключи K ₂ размыкаются, а ключ K 1 замыкается, в результате чего, управляющий сигнал подается непосредственно на объект.

Таким образом, были рассмотрены задачи управления технологическими объектами и их производственными образованиями в условиях малой априорной информации, в частности, в условиях непараметрической неопределенности. При этом уделяется специальное внимание типичным для практического случая процессам, когда дискретность измерения выходной переменной процесса промышленного комплекса происходит через существенные интервалы времени, что обуславливает особенности при постановке задач идентификации и управления. Приводятся алгоритмы управления и принятия решений в иерархических системах управления в условиях неполной информации. Рассматривается также схема построения контура управления с идентификатором, которую естественно применять для процессов, имеющих существенное значение.

Следует обратить внимание на эффективность использования непараметрических моделей и алгоритмов в интеллект-системах управления и принятия решений для предприятий и отраслей с непрерывным характером технологического процесса.

Библиографическая ссылка

1. Медведев А. В. О моделировании организационных процессов // Вестник Сиб. гос. аэрокосмич. ун-т им. акад. М. Ф. Решетнева : сб. науч. тр. / под ред. проф. Г. П. Белякова. Вып. 1. Красноярск, 2000.

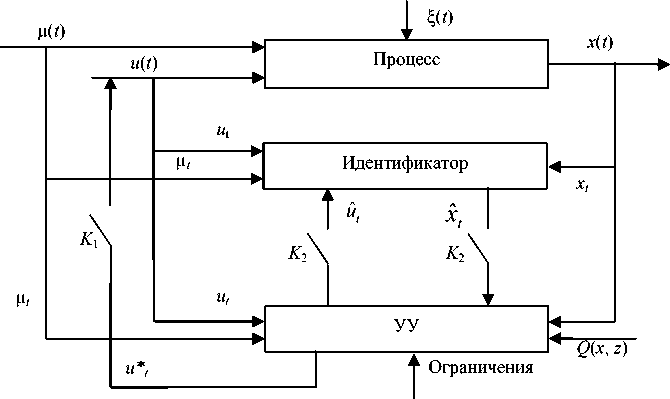
Рис. 7. Система управления с идентификатором

D. A. Ignatyev, A. N. Sergeev

NONPARAMETRIC MODELING OF ORGANIZATIONAL PROCESSES

Some modeling and managing problems of organizational systems under conditions of uncertainty are discussed in the article. Some peculiarities of organizational processes which take place in different technical and technological objects are mentioned in comparison with other processes. Nonparametric model of organizational systems and decision-making algorithms when information is not complete is offered.