Непараметрическое оценивание количества классов, отличающихся средней яркостью, на тепловизионных изображениях
Автор: Галянтич А.Н., Райфельд М.А.
Журнал: Компьютерная оптика @computer-optics
Рубрика: Обработка изображений, распознавание образов
Статья в выпуске: 5 т.47, 2023 года.
Бесплатный доступ
При синтезе алгоритмов автоматической пороговой сегментации изображений по яркостному признаку важной информацией является количество яркостных классов и, как следствие, проблема определения числа порогов. Решение задачи оценивания количества классов на изображении может базироваться на представлении его распределения в виде смеси распределений яркостных классов с неизвестными априорными вероятностями либо оценке количества мод гистограмм. При этом известно, что задача расщепления смеси имеет решение лишь для некоторых видов распределений, а моды гистограммы не всегда различимы. В общем случае, когда распределения яркостных классов неизвестны, возникают трудности применения указанных методов. В статье предлагается непараметрический подход к определению количества классов, отличающихся средней яркостью, основанный на ранговых гистограммах и использующий свойство локальной пространственной группировки элементов каждого яркостного класса на изображении.
Сегментация изображений, непараметрический алгоритм, гистограмма рангов, собственные числа, ортогонализация грамма-шмидта, метод главных компонент
Короткий адрес: https://sciup.org/140301847
IDR: 140301847 | DOI: 10.18287/2412-6179-CO-1284
Текст научной статьи Непараметрическое оценивание количества классов, отличающихся средней яркостью, на тепловизионных изображениях
В настоящее время распознавание изображений широко используется в различных областях науки и производства. В связи с успехами в области компьютерных технологий наблюдаются значительные достижения в методах распознавания изображений. Несмотря на значительное распространение нейросетевых технологий в задачах распознавания образов, существуют задачи обработки изображений, которые используют классические статистические подходы к решению данной проблемы, поскольку не всегда возможно получить достаточный объём данных для надёжного обучения нейросети. Процедуре распознавания в этом случае, как правило, предшествует операция сегментации изображения, имеющая своей целью разбиение сложного изображения на области, отсчёты которых обладают сходными статистическими и корреляционными свойствами. По существу, при этом решается задача статистической классификации точек изображения по некоторым информационным признакам. Достаточно часто сегментация осуществляется по яркости с использованием простейшего метода пороговой обработки [1].
Существует большое количество математически строго обоснованных, а также эвристических алго-
ритмов сегментации изображений, опирающихся на различные оптимизационные критерии и информационные признаки областей. При этом часто предполагается наличие полной априорной информации о статистических и корреляционных свойствах классов, например, в виде многомерного распределения яркости. При любых отклонениях статистических свойств реальных изображений от модели алгоритмы сегментации, ориентированные на полную априорную информацию о свойствах классов, могут терять работоспособность. Поэтому значительное распространение получили параметрические и адаптивные алгоритмы сегментации изображений, опирающиеся на представление об известном виде распределения наблюдений, параметры которого оцениваются по исходным данным. Здесь можно отметить известный подход к задаче сегментации изображений, содержащих точки нескольких классов, как к задаче расщепления смеси распределений известного вида [2]. В ряде задач информация о виде распределения недоступна (или это распределение может меняться в процессе наблюдения). В этом случае часто применяются непараметрические методы, базирующиеся на непараметрических оценках распределений яркости и самых общих представлениях о различии статистических свойств классов. К непараметрическим относятся многочисленные методы, основанные на анализе гистограммы (непараметрической оценке плотности вероятности наблюдений).
1. Постановка задачи оценки количества классов на изображении
Существует разновидность изображений, отображающих объекты, наиболее важным информационным признаком которых является их средняя яркость. При этом точки объектов группируются в связные области произвольной формы на изображении. К изображениям такого типа относятся, например, тепловизионные изображения, яркость локальных областей которых определяется температурой соответствующих объектов (рис. 1 а ).

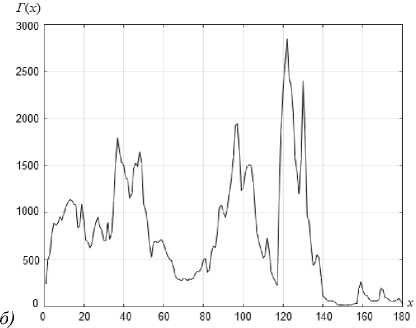
Рис. 1. Пример реального тепловизионного изображения (а)
и его гистограмма (б)
Содержательная задача может заключаться в выделении нагретых объектов. Применение простейшего метода квантования мод гистограммы [3] в этом случае не всегда является приемлемым, поскольку тепловизионные изображения искажены шумом (плотность вероятности которого, как правило, неизвестна) и, кроме того, яркость точек локальных областей характеризуется случайной текстурой, зависящей от физических свойств отображающихся объектов, поэтому главные моды гистограммы не всегда возможно выделить. Так, например, на рис. 1б представлена гистограмма изображения, приведенного на рис. 1а. При использовании того или иного подхода к сегментации важным параметром изображения является количество классов K, присутствующих в его яркостных (или цветовых) данных. Без знания этого параметра ряд методов сегментации (например, основанный на расщеплении смеси [4, 5]) не обладает работоспособностью. Совместная оценка параметров смеси распределений и оценка количества этих распределений (даже при известных их видах) сопряжены с известными проблемами. Так, например, общее равномерное распределение яркости одного класса может быть представлено несколькими способами в виде смеси двух равномерных распределений с различными параметрами. Поэтому с помощью гистограммы не всегда можно однозначно различить компоненты смеси и оценить их параметры. При решении задачи оценки числа классов на изображении на основе максимально правдоподобного подхода может наблюдаться смещение этой оценки в сторону больших значений этого параметра. В критериях, используемых при определении числа компонентов смеси нормальных распределений, применяемых совместно с EM-алгоритмом, эта проблема решается введением специального слагаемого, компенсирующего рост функции правдоподобия, которое приводит к появлению экстремума в зависимости от числа компонентов. На этом подходе основан критерий Акаике [6], Байесовский информационный критерий (также известный как критерий Шварца) [7] и ряд других.
-
2. Использование рангового подхода для оценки количества классов на изображении в условиях априорной неопределённости
В данной работе предложен способ решения задачи оценивания количества классов, отличающихся средней яркостью, на изображениях в условиях непараметрической априорной неопределённости, основанный на построении гистограммы рангов изображения. Предположим, что в простейшем случае диапазон яркости каждого из классов не перекрывается с диапазонами яркости других классов изображения. Иными словами, яркость любой точки, принадлежащей классу 5 к , меньше яркости любого отсчёта классов 5 к+1,..., 5 к и больше яркости любого отсчёта классов 5 1,..., 5 к -1 (метки классов 5 1,..., 5 k —1 , 5 к , 5 к +1,..., 5 к упорядочены в соответствии с яркостью их отсчётов). Формальная запись данного утверждения может быть представлена в виде:
-
1 1, x e5i , l = к + 1, к + 2,.... K Fk ( x ) = i ,
I 0, x e5 1 , l = к - 1, к - 2,....1
где Fk (x) – функция распределения класса с меткой 5к. В этом случае вне зависимости от вида функции распределения яркости каждого из классов распреде- ление ранга отсчёта, принадлежащего классу 5k, является равномерным в диапазоне, зависящем от общего количества точек данного класса Lk (при независимых отсчётах). Пусть ранг каждого отсчёта вычисляется на основе вариационного ряда, составленного из яркостей всех точек изображения. Понятно, что в случае неперекрывающихся классов существует набор яркостных Cx = {Cx 1, Cx2,. ^, Cxn} (либо ранговых Cr ={Cr 1, Cr2,...., Crn}) порогов, позволяющих безошибочно разделять отсчёты различных классов. Однако оценивать этот набор порогов приходится по имеющемуся изображению, что в случае непараметрической априорной неопределенности и в отсутствие информации о количестве классов на изображении является крайне непростой и даже в ряде случаев неразрешимой задачей. Описанная выше модель непе-рекрывающихся яркостных классов является в достаточной степени искусственной, поэтому реальные изображения, как правило, не соответствуют ей в точности. Тем не менее, эта модель может использоваться для синтеза непараметрического алгоритма оценивания количества классов на изображении. Более слабым предположением, позволяющим расширить применимость описанной выше модели, является утверждение, что отсчёты класса 5k менее яркие, чем отсчеты классов 5k+1,..., 5K, и более яркие, чем 51,..., 5k-1, но лишь в статистическом смысле. Данная модель является более реалистичной, поскольку реальные изображения, как правило, искажены шумами. Вместо (1) в этом случае можно записать систему следующих условий:
J F k ( x ) > Fz ( x ), l = k + 1,..., K [ Fk ( x ) < Fl(x ), l = 1,..., k - 1 .
Системе неравенств (2) удовлетворяют, например, классы, яркости которых характеризуются функциями распределения одного вида, отличающиеся сдвигом (с произвольным знаком). Таким образом, справедливы следующие уравнения:
F k ( x ) = F ( x — A ki ),
A ki = E ( x ; x e5 k ) - E ( x ; x e5 1 ), (3)
l = 1,..., k -1, k +1,..., K, где E (x; x^5k) - математическое ожидание яркости отсчётов класса 5k. К подобному типу относятся изображения, состоящие из областей, представленных отсчётами постоянного уровня яркости, на которые наложен независимый шум. В этом случае распределение ранга отсчётов каждого класса приближается к равномерному, но на границах имеет отклонение. Большинство реальных изображений являются нестационарными. Это означает, что отсчёты каждого яркостного класса не рассеяны равномерно по всему изображению, а группируются в некоторой его локальной области (что не учитывается в моделе смеси). Следовательно, если
отсчё т изображения x i , j принадлежит k -му классу ( k = 1, K ), то точки из окрестности Q ( i , j ), в которую входит и x i , j , будут принадлежать тому же классу с вероятностью, большей чем 1/ K .
Далее рассмотрим подходы к решению задачи оценивания общего количества классов на изображении. Одним из возможных способов её решения может служить итеративная процедура, предполагающая предварительное задание количества классов, определение яркостных порогов (при данном количестве классов), оценка качества последующей сегментации изображения. Однако на этом пути возникает проблема с выработкой критерия для останова итеративной процедуры и значительные вычислительные затраты, связанные с перебором или оценкой порогов сегментации в условиях априорной неопределённости. Рассмотрим другой подход к получению оценки K̂ . Покажем, как для нестационарных изображений, состоящих из отсчётов классов, распределение яркости которых описывается в соответствии с (2), можно получить оценку общего количества классов на изображении (т.е. K̂ ), не производя процедуры сегментации. Пусть имеется изображение размера n = N × M , отсчёты классов которого удовлетворяют условию (2). Каждому отсчёту этого изображения поставлен в соответствие его ранг r , r е 1, n из общего вариационного ряда. В том случае, если распределения классов не перекрываются (1), то, как было отмечено выше, распределение рангов их отсчётов не зависит от распределения яркости наблюдений, а является равномерным с параметрами, зав ися щими от количества точек каждого класса Lk , k = 1, K на всём изображении:
P k ( r ) =
1/ L k ,
rk - 1max < r — rk max
0, иначе
где r k –1max и r k max = r k –1max + L k – соответственно максимальные ранги элементов k –1-го и k классов (номера классов упорядочены по яркости). Сформируем не сколько неперекрывающихся выборок Q p , p = 1, P одинакового размера, включающих все элементы исходного изображения. Выборки можно сформировать, например, как показано на рис. 2, из точек прямоугольных окон размера n p = N p × M p .
|
1 |
2 |
|
3 |
4 |
Рис. 2. Возможный вариант формирования выборок из отсчётов изображения
Каждая выборка состоит из отсчётов различных классов. Поэтому распределение ранга отсчёта выборки p , принадлежащего классу 5 k , является равномерным (4) и определяется количеством точек этого класса в данной выборке g k , p : P k , p ( r ) = P k ( r ) g k , p In p . Безусловное по отношению к номеру класса распределение ранга выборки p запишется в виде:
K
P p ( r ) = Z P k ( r ) g kj n p . (5)
k = 1
Таким образом, в соответствии с уравнением (5) распределение ранга отсчёта выборки Qp представляет собой комбинацию дискретных равномерных распределений с примыкающими границами (4), взятых с весовыми коэффициентами, зависящими от количества элементов каждого из классов g k , p в выборке Q p . На рис. 3 представлен пример распределения рангов для четырёх выборок ( P = 4) изображения в случае, если яркость его отсчётов принадлежит одному из трёх классов ( K =3) (предполагается, что распределения яркости классов не перекрываются). Очевидно, что если просуммировать (с соответствующей нормировкой 1I P ) распределения всех выборок, то получим равномерное распределение рангов
[ 1I n , 0 < r < n
P ( r ) = ) .
[ 0, иначе
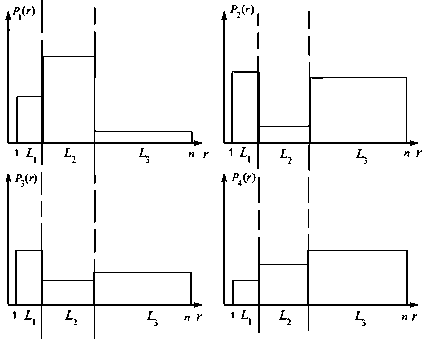
Рис. 3. Пример распределений ранга в выборках изображения с неперекрывающимися яркостными классами
3. Применение метода главных компонент к ранговым гистограммам выборок изображения
Рассмотрим распределения рангов Pp (r), p = 1, P выборок изображения для модели неперекрываю-щихся классов (рис. 3) как функции r, rе1, n. Оценками функций Pp (r) могут служить гистограммы рангов Pp (r), полученные для соответствующих выборок. Можно отметить, что кусочно-постоянные дискретные функции Pp (r) различных выборок претерпевают скачок при одних и тех же значениях абсцисс, зависящих от количества классов и количества точек этих классов на изображении. Известно, что подобные функции можно представить в пространстве размерности, меньшей чем n. Размерность собственного базиса в этом случае на единицу больше количества скачков и равна числу классов на изображении K. Для построения собственного базиса можно воспользоваться одним из двух способов. Во-первых, использовать процедуру Грамма-Шмидта [8], либо, во-вторых, воспользоваться методом главных компонент [9]. Метод главных компонент заключается в нахождении линейного преобразования функций ранговых гистограмм выборок (строчных векторов длиной n): Pp (r)={ Pp (1), Pp (2),., Pp (n)}, p = 1 ,P, приводящего к представлению этих векторов Z в новой системе координат:
Z = PV , (6)
где
P 1 ( r )
P =
P 2 ( r )
, p = 1 ,P ,
P p ( r )
-
а V - базис собственных векторов.
Метод главных компонент предполагает нахождение собственных векторов и собственных чисел корреляционной матрицы R функций P p ( r ) размерности P х P . Эту корреляционную матрицу можно найти следующим образом:
R = PP T =
P ( r ) P ( r ) T Pl ( r ) P 2 ( r ) T .. P 1 ( r ) P p ( r ) T
P ( r ) P 1 ( r ) T P z( r ) P z ( r ) T .. P z( r ) P p ( r ) T
Pp (r) P1( r) T .. .. Pp (r) Pp (r) T здесь Pp - функция распределения рангов i-й выборки изображения, записанная в виде строчного вектора Pp (r)={ Pp (1), Pp (2),..., Pp (n)}, p = 1 ,P . Матрица собственных векторов V, диагональная матрица Л, содержащая на главной диагонали собственные числа {Х1, Х2,.ХP}, и корреляционная матрица R связаны известным матричным уравнением: R = VAVT. При этом количество диагональных элементов матрицы Л, отличных от нуля, и определяет размерность собственного базиса (количество классов на изображении). Поскольку максимальное количество отличных от нуля собственных чисел равно P, то из этого следует, в частности, что количество ранговых гистограмм (количество сформированных из несовпадающих наблюдений выборок Pp (r)), которые используются для вычисления корреляционной матрицы (7), определяет «исходную» размерность пространства. Эта «исходная» размерность должна быть, по край- ней мере, больше ожидаемого количества классов на изображении. Таким образом, количество выборок, с одной стороны, должно быть достаточно большим, но, с другой стороны, увеличение количества выборок приводит к уменьшению их объёма, что снижает качество оценки ранговых гистограмм. Таким образом, необходимо иметь начальное представление (достаточно приблизительное) о возможном количестве классов на изображении. Также существует возможность установить (по превышению минимального собственного значения порога), что количество классов больше, чем предполагалось.
Вследствие того, что ранговые гистограммы P̂ p ( r ) представляют собой оценки соответствующих распределений рангов и являются кусочно-постоянными функциями лишь в статистическом смысле, то в случае реальных изображений, как правило, все собственные числа X отличны от нуля. Однако их значения, изменяющиеся в широких пределах, дают представление о мощности проекций на соответствующий собственный вектор ортогонального базиса. Среди всех P компонент можно выбрать G «значимых» ( G < P ), в которых сосредоточена основная мощность. Метод главных компонент предполагает упорядочивание по X i векторов в ортогональном базисе. Так, первой главной компонентой в этом случае является линейная комбинация исходных векторов P , которая обладает наибольшей дисперсией Х 1. Количество классов определяется числом «значимых» главных компонент, выделяемых в результате сравнения соответствующих им собственных чисел с некоторым порогом Х ^ , определяемым по распределению собственных чисел [10, 11].
Необходимо отметить, что для оценки числа главных компонент можно также использовать эвристическое правило Кайзера [12] или правило сломанной трости [13]. Выше было отмечено, что гистограммы рангов выборок P̂p (r) являются оценками соответствующих распределений рангов. Эти гистограммы являются случайными функциями вследствие случайного распределения количества отсчётов каждого класса в выборках изображения. Поэтому даже при строгом выполнении условия (1) их применение приводит к появлению ошибок при оценивании количества классов K̂ на изображении. При этом использование рангов приводит к независимости вероятности ошибок от вида функции распределения яркости классов (при неперекрывающихся распределениях классов), т.о. эти оценки обладают непараметрическим свойством. Статистические характеристики ранговых гистограмм не зависят от вида распределения яркости класса, а определяются общим количеством его отсчётов Lk на изображении и распределением его элементов по выборкам gk,p. Найдём распределение отсчетов гистограммы рангов P̂p выборки Qp. Вероятность P̂p (r) оценивается (в соответствии с определением гистограммы) как количество рангов, попав- ших в некоторый интервал Ar, j = 1, T, построенный вокруг значения r по выборке Qp (Ar - размер интервала, T – количество интервалов), отнесённое к длине интервала. Будем полагать, что каждый из ранговых интервалов Ar содержит элементы только одного класса изображения (например, 5k). Таким образом:
P p ( r ) = q k , p /( A r n p ), (8)
где q k,p – количество рангов выборки Q p , принадлежащих классу k , попавших в интервал A r . Учитывая, что знаменатель в (8) является детерминированной величиной, распределение оценки P̂ p ( r ) совпадает с распределением q k,p , которое вычисляется достаточно просто:
-
f gk —A r YA r Y gk 1
P ( q k , p ) = I II II I . (9)
-
у g k , p q k , p у у q k , p J у g k , p у
- Из полученного выражения следует, что распределение отсчётов гистограммы рангов обладает непараметрическим свойством. На основе выражения (9) можно рассчитать математическое ожидание и дисперсию отсчета ранговой гистограммы P̂p (r):
M [ P , ( r )] = —, g k n p
D[ Pp (r)] = f gk,p (gk,p — 1)(Ar -1) + gk,p I - f gk,p )2 (10)
I g k ( g k - 1) A r g k A r J у g k J
= .
n 2 p
Из выражения (10) следует, что минимальная дисперсия отсчёта гистограммы (равная нулю) получается в случае, если g k,p = g k (все точки k -го класса сосредоточены в выборке p ) либо g k,p =0 (ни одного элемента этого класса нет в выборке). Дисперсия максимальна, если g k,p = g k /2. Она в этом случае равна D max =1/(4 A r ), т.е. определяется только параметрами алгоритма расчёта гистограммы. Ранговый алгоритм не будет обладать работоспособностью, если количество точек каждого класса в о кне у до влетворяет равенству: g k , p = g k n p( n , k = 1, K , p = 1, P , которое говорит о равномерном рассеянии точек различных классов по изображению. Предлагаемый метод оценивания количества классов был испытан на тестовом изображении, приведённом на рис. 4 а . Тестовое изображение имеет размер 128 ×128 и состоит из пикселей, принимающих один из девяти возможных уровней яркости (рис. 4 б ). Причём точки каждого уровня группируются в локальную область на изображении, т.е. могут рассматриваться как отдельный класс. Наложение независимого шума на исходное изображение приводит к «размыванию» границ между классами (рис. 4 в ), что делает проблематичным корректное определение числа классов на изображении с помощью гистограмм яркости.
б)
в)
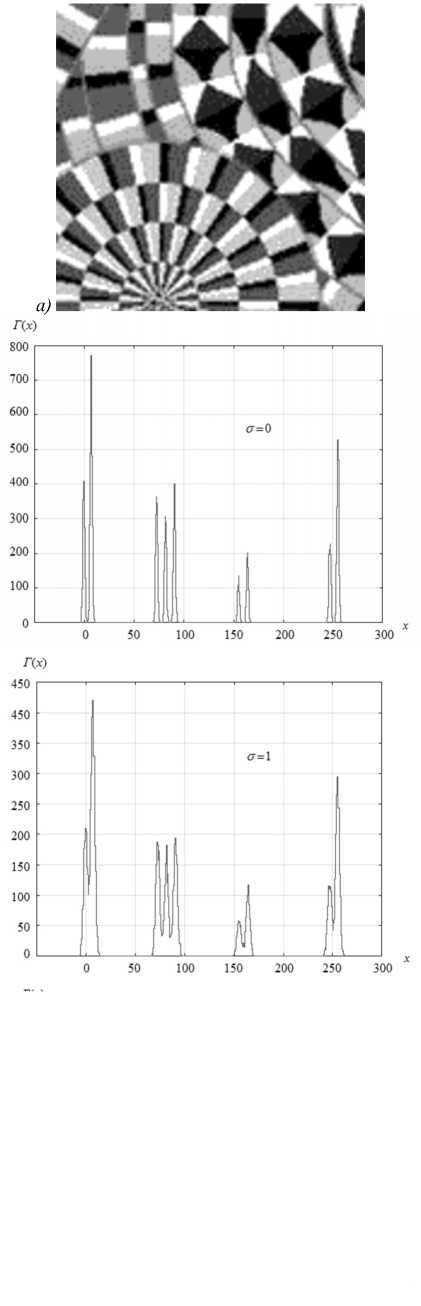
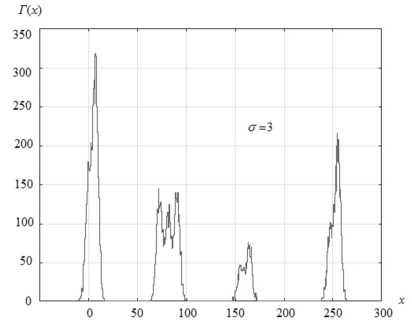
Рис. 4. Гистограммы тестового изображения (а) при различных уровнях СКО шума ( σ ) (б, в, г)
г)
В результате использования предлагаемого выше рангового алгоритма удаётся с заданной вероятно- стью ошибки достаточно уверенно оценивать количество классов (рис. 5).
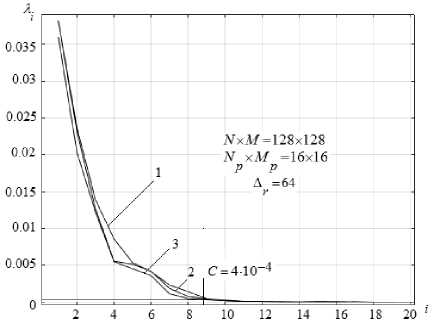
Рис. 5. Значения собственных чисел, полученных для корреляционной матрицы гистограмм R при различных уровнях шума. Кривая 1– σ = 0, 2 – σ = 1, 3 – σ = 3
На основе представленных с помощью рис. 4 и 5 результатов можно сделать следующий вывод. Несмотря на то, что выделение мод гистограмм яркости с увеличением уровня шума становится всё более затруднительным, метод, ориентированный на анализ значений собственных чисел локальных ранговых гистограмм, даёт устойчивые результаты количества классов (уровней яркости) на изображении.
-
4. Сравнение предлагаемого метода оценки количества яркостных классов на изображениях с существующими алгоритмами
Сравнение предлагаемого метода (метода главных компонент (МГК) корреляционной матрицы ранговых гистограмм) оценки количества классов на изображении с известными методами (критерием Акаике (AIC) [14], байесовским информационным критерием (BIC) [7]) проводился с использованием тестового изображения (320 ×240 пикс.), состоящего из пяти яркостных классов (рис. 6 а ). Синтетическое изображение формировалось в результате наложения случайных текстур с различными спектральными характеристиками и независимых отсчётов шума (рис. 6 б ). Гистограмма искусственного изображения, приведенная на рис. 6 в , демонстрирует проблемы сегментации и оценки количества классов на изображениях.
В параметрическом методе на основе байесовского критерия использовался EM-алгоритм оценки параметров смесей нормальных распределений [15]. Классы на изображении моделировались нормальным законом, с равной дисперсией σ 2 =0,5 и равномерно возрастающим математическим ожиданием (на единицу) от класса к классу: m k+1 = m k +1, k =1 … 5, m 1 =0. Выборки формировались из отсчётов прямоугольных фрагментов изображения размера 32×40 пикселей (всего 60 выборок). Результаты сравнения сведены в табл. 1.
а)


в)
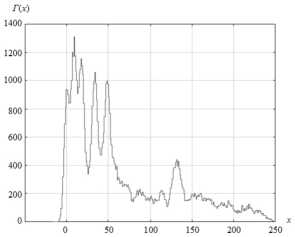
Рис. 6. Формирование модельного изображения: исходное искусственное изображение (а) и результат искажения шумом и размазывания (б), гистограмма искажённого изображения (в)
Табл. 1. Результаты статистического эксперимента по определению количества яркостных классов на изображении
|
Количество классов – 5 |
Метод |
Вероятности оценок количества классов |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
||
|
AIC |
0 |
0 |
0 |
0,07 |
0,67 |
0,26 |
|
|
BIC |
0 |
0 |
0,01 |
0,1 |
0,60 |
0,29 |
|
|
МГК |
0 |
0 |
0 |
0,05 |
0,85 |
0,10 |
|
Работоспособность алгоритма на основе МГК корреляционной матрицы ранговых гистограмм была проверена также на реальном изображении, приведённом на рис. 1 а.
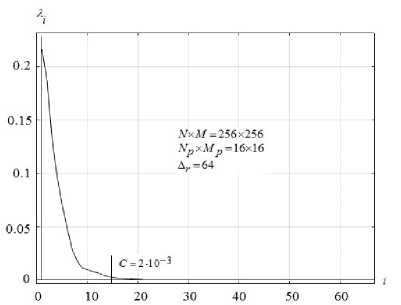
Рис. 7. Значения собственных чисел, полученных для корреляционной матрицы гистограмм R реального тепловизионного изображения (рис. 1а)
Значения собственных чисел корреляционной матрицы приведены в виде графика на рис. 7. Оценка количества яркостных классов оказалась равной 14, что близко к ожидаемому значению.
Заключение
В статье предложен подход к оцениванию количества яркостных классов на изображениях. Предлагаемый метод основан на особом свойстве локальных (построенных по несовпадающим фрагментам) ранговых гистограмм неоднородного изображения, которые рассматриваются как векторы. Данное свойство заключается в возможности их эффективного представления в пространстве меньшей размерности (собственном базисе). Размерность собственного базиса в случае ранговых гистограмм и является оценкой количества классов на изображении. Таким образом, при получении данной оценки можно использовать процедуру Грамма– Шмидта (для построения собственного базиса и определения его размера) либо воспользоваться методом нахождения собственных чисел и векторов корреляционной матрицы локальных ранговых гистограмм, построенной для изображения. В статье развит второй подход. Было показано, что предлагаемый подход обладает непараметрическим свойством, поскольку распределение отсчёта ранговой гистограммы не зависит от вида функции распределения яркости исходного изображения. Это позволяет контролировать вероятность ошибки при принятии решения о числе классов в результате сравнения с заранее рассчитанным порогом значений собственных чисел. Развиваемый в статье подход может быть использован в задачах автоматической обработка тепловизионных изображений и, в частности, их сегментации.
Список литературы Непараметрическое оценивание количества классов, отличающихся средней яркостью, на тепловизионных изображениях
- Chochia PA. Image segmentation based on analysis of distances in feature space. Optoelectron Instrum Data Process 2015; 50(6): 613-624. DOI: 10.3103/S8756699014060107.
- Aivazyan SA, Buchstaber VM, Yenyukov IS, Meshalkin LD. Applied statistics: classification and reduction of dimensionality. Moscow: "Finansy i Statistica" Publisher; 1989. ISBN: 5-297-00054-X.
- Sezgin M, Sankur B. Survey over image thresholding techniques and quantitative performance evaluation. J Electron Imaging 2004, 13(1): 146-168. DOI: 10.1117/1.1631315.
- Kittler J, Illingworth J. Minimum error thresholding. Pattern Recogn 1986, 19(1): 41-47. DOI: 10.1016/0031-3203(86)90030-0.
- Devijver PA, Kittler J. Pattern recognition: A statistical approach. Englewood Cliffs, NJ: Prentice Hall; 1982.
- Akaike H. A new look at the statistical model identification. IEEE Trans Automat Contr 1974, 6(1): 716-723. DOI: 10.1109/TAC.1974.1100705.
- Schwarz G. Estimating the dimension of a model. Annals of Statistics 1978, 6(2): 461-464. DOI: 10.1214/AOS/1176344136.
- Podrezov RV, Raifeld MA. Nonparametric method of estimating number of classes in image segmentation. Optoe-lectron Instrum Data Process 2020; 56(3): 280-287.
- Andrukovich PF. Application of the principal component method in practical research. Moscow: "Izdatel'stvo mos-kovskogo universiteta" Publisher; 1973.
- James AT. The distribution of the latent roots of the covar-iance matrix. Ann Math Statist 1960; 31(1): 151-158. DOI: 10.1214/aoms/1177705994.
- Anderson GA. An asymptotic expansion for the distribution of the latent roots of the estimated covariance matrix. Ann Math Statist 1965; 36(4): 1153-1173. DOI: 10.1214/aoms/1177699989.
- Kim J-O, Mueller CW. Factor analysis: Statistical methods and practical issues. Newbury Park, CA: Sage Publications Inc; 1978. ISBN: 978-0-8039-1166-6.
- Cangelosi R, Goriely A. Component retention in principal component analysis with application to cDNA microarray data. Biology Direct 2007; 2: 2.
- Akaike H. A Bayesian analysis of the minimum AIC procedure. Ann Inst Statist Math 1978; 30(A): 9-14. DOI: 10.1007/BF02480194.
- Korolev VY. EM-algorithm, its modifications and their application to the problem of separation of mixtures of probability distributions. Moscow: IPI RAN Publisher; 2007.


