Непланарные графы, двойственные сети, закон сохранения потока энергии: фундаментальная проблема, которая пока не решена

том 21 № 3 (68), 2025, ст. 1

Технические, экономические, биологические системы состоят из элементов, связи которых между собой образуют структуру. В элементах протекают процессы в виде потоков одних величин под действием других величин при сопротивлении материи элементов. Системы растут, элементов становится больше, структура связей сложнее. Скорость обновления систем, их структуры связей, включая системы вооружений, требует применения моделей, представляющих такие изменения. Для анализа и управления надо создавать модели, которые представляют процессы в системе, и обеспечивают расчет их изменения при изменении структуры связей.

Сетевые модели представляют процессы и структуру сложных технических, экономических, биологических систем, позволяя анализировать изменения процессов при изменении структуры. Структура представляет свойства пространства нашего мира, которые стали проявляться при росте сложности систем. Сети представляют параметры процессов как компоненты, проекции в системы координат пространства структуры. Координатами являются замкнутые и разомкнутые пути. Они образуют два независимых, и при этом взаимно дополняющих друг друга подпространства.

Пионер тензорного анализа сетей Г. Крон рассматривал набор ветвей как тензор, а соединения ветвей в разные сети – как проекции этого тензора в частные системы координат. В методе Крона было две проблемы. Для получения формулы преобразования напряжения он постулировал, что мощность в сети не меняется при изменении соединения ветвей. Это критиковали, поскольку мощность при этом меняется. Но полученные формулы давали правильные результаты при расчете сетей, а также созданных на их основе сетевых моделей технических и экономических систем. Проблему инварианта мощности Крона безуспешно пытались решать сотрудник Эйнштейна Б. Гоффман (B. Hoffmann) [3–4], тополог Дж. Росс (J.P. Roth) [6–7], сотрудник Крона по Дженерал Электрик Х. Хэпп [8, 1974] и другие.

Другая проблема состояла в том, что матрицы преобразования путей в общем случае прямоугольные, и они не имеют обратных. Пути являются координатами в пространстве структуры, т.е. пространстве, которое существует только вдоль элементов сети, системы. При изменении соединений ветвей размерность базисов замкнутых и разомкнутых путей меняется. При слиянии границ ветвей разомкнутый путь превращается в замкнутый, и наоборот. При этом меняется размерность подпространств этих путей, а значит матрицы преобразования путей становятся прямоугольные. Такие матрицы не имеют обратных, и получается, что из описания соединения ветвей нельзя представить разъединение ветвей.

Противоречие с неправильным постулатом об инварианте мощности, который дает правильные результаты, разрешил автор [10–12, 32–34]. Оказалось, что мощность в двух сетях с двойственной структурой постоянная при изменении соединения их ветвей, хотя в каждой сети мощность меняется. При этом увеличению, например, числа контуров в одной сети, соответствует уменьшение числа контуров в двойственной сети, и можно с помощью инварианта двойственности получить решение формально «вырожденной» задачи.

Таким образом, проблема постулата Крона об инварианте мощности была решена, также как и проблема прямоугольных матриц преобразования. Однако возникла другая проблема, которая может стать новой точкой развития знания о свойствах нашего мира.

Инвариант двойственности пространства представляет собой постоянство суммы метрических тензоров двойственных сетей при изменении их структуры, даже когда в сети нет потоков, процессов. Когда в сети есть процессы, воздействия и отклики, то инварианту двойственности соответствует постоянство суммы мощностей, потока энергии, в двух сетях с двойственной структурой. Это физический закон сохранения, такого же типа, как и уже известные, которые связаны с разными видами симметрии пространства и времени. Закону сохранения энергии соответствует симметрия времени, закону сохранения импульса соответствует симметрия (однородность) пространства, закону сохранения момента импульса соответствует симметрия направлений в пространстве (изотропия). Закону сохранения потока энергии, который измеряется мощностью, соответствует двойственность пространства. Речь идет, конечно, о замкнутых системах.

Двойственность структуры является свойством самого пространства, которое состоит в том, что сами сети как элементы пространства, без потоков энергии, без физических величин, обладают инвариантом двойственности.

Законы сохранения определяют свойства пространства или свойства пространства определяют законы сохранения? Есть ли «пустое» пространство без материальных объектов, образующих замкнутые системы? Инвариант двойственности для одномерных сетей является математическим требованием существования другого пространства, двойственного по отношению к нашему пространству. Наше пространство существует вместе с дополнительным, двойственным пространством, с которым они составляют единое целое.

Поток энергии, измеряемый мощностью, распределяется между двумя двойственными сетями. Величина мощности в каждой из них зависит от структуры соединения ветвей, но сумма мощностей постоянна. Таким образом, мощность является инвариантом относительно преобразования структуры двойственных сетей.

Инварианты двойственности для многомерных сетей, которые еще не открыты, могут указать на многообразие пространств, в которых координатами являются многомерные пути. Одномерные замкнутые и разомкнутые пути – это линии, но они фундаментально различны. Замкнутый путь можно выразить через разомкнутые пути. Разомкнутый путь нельзя выразить через замкнутые пути. Разомкнутый путь одномерный – это линия, отрезок. Замкнутый путь – это также линия, но она охватывает двумерную поверхность, то есть, вводит новое измерение. Аналогично, замкнутый двумерный путь, состоящий из граней, охватывает трехмерный объем, т.е. вводит следующее новое измерение. И так далее…

В двойственных сетях существует проблема непланарных графов, т.е. таких, которые нельзя изобразить на плоскости без самопересечения ветвей, ребер. Для сетей, представленных такими графами, нельзя представить, показать двойственную сеть. Куратовский доказал, что есть только два таких непланарных графа. Рассмотрим эти графы, и возникающие в них проблемы, которые имеют вид противоречия.

Противоречие постулата Крона, состояло в том, что неправильное допущение дало правильный метод расчета. Разрешением этого противоречия стало открытие инварианта двойственности. Пока нет ясности, чем станет разрешение противоречия между существованием решения задачи сети для непланарных графов, и невозможностью изобразить структуру, конструкцию таких сетей.

Непланарность графов и двойственность сетей

В двойственных сетях существует особенность, которая имеет характер противоречия. Нельзя наглядно построить граф с двойственной структурой для непланарного графа. Для непланарного графа двойственный граф не существует. На эту особенность указал автору в 1984 г. В.А. Горбатов.

С одной стороны, это вносит теоретические трудности в инвариант двойственных сетей. А, следовательно, и в постоянство мощности при изменении структуры двойственных цепей, в закон сохранения потока энергии. Как только изменение структуры сети приводит к возникновению в ней непланарного графа, двойственная сеть как бы перестает существовать, во всяком случае, ее нельзя представить наглядно. Это должно создавать трудности при измерении результатов и т.д. Вместе с тем, как только в процессе изменений структуры непланарность в сети исчезает, то для нее снова существует двойственная сеть. Это указывает, что существует какая-то, еще не известная закономерность, с которой связаны такие эффекты.

Противоречие между постулатом об инварианте мощности Крона и реальным изменением мощности в электрической цепи при изменении структуры открыло, что существуют сети с двойственной структурой, с инвариантом, который связывает изменения структуры двойственных сетей. Для двух двойственных цепей, а не для одной, выполняется закон сохранения потока энергии. Это разрешило противоречие Крона в соответствии с принципами диалектики. Нечто подобное должно быть и для двойственных инвариантов в условиях непланарности. Разрешение данного противоречия может открыть новые свойства, касающееся характера границ, связывающих двойственные сети, и механизма взаимодействия этих сетей при изменении структуры, которые пока неизвестны.

Итак, теория графов утверждает, что двойственный граф можно построить только для планарного графа. То есть, для такого графа, который можно изобразить на плоскости без самопересечения ветвей (ребер). Непланарный граф не имеет двойственного графа ([9, 1984]. Невозможность построить двойственный граф к непланарному графу, связана с тем, что в области, где ветви пересекаются, нельзя однозначно указать, в каком именно контуре должен располагаться соответствующий узел двойственного графа (сети). То есть, иначе говоря, неоднозначность построения вызвана тем, что двум независимым контурам (циклам) в данном графе соответствует только один узел (вершина) в двойственном графе.

Доказано, что только два графа лежат в основе проблемы отношений между двойственности и непланарности. Первый из них – это так называемый «двудольный» граф, обозначаемый K₃,₃ , в котором каждая из трех «верхних» вершин связана с каждой из трех «нижних» вершин. Всего такой граф содержит 9 ветвей-ребер. Второй, обозначаемый K 5 , представляет собой пятиконечную звезду, связанную по периметру. Это полный граф на пяти вершинах, т.е. каждая из вершин связана со всеми остальными вершинами ребрами (ветвями). Всего здесь 10 ветвей-ребер. Следовательно, пространство одной из таких непланарных сетей имеет 9 измерений, а другой – 10 измерений.

Эти два непланарных графа, известные как графы Куратовского, [5, 1966], а именно, K 3,3 и K 5 используют для доказательства того, что непланарный граф не имеет двойственного графа. Сначала доказывают, что для этих графов двойственные графы не существуют, а затем доказывают, что любой непланарный граф содержит либо K 3,3 , либо K 5 . Теорема Понтрягина — Куратовского формулируется так: — граф планарен тогда и только тогда, когда он не содержит подграфа, который является подразделением K₅ или K₃,₃ (иначе говоря, когда он не содержит подграфа, гомеоморфного графу K₅ или K₃,₃ ) [9, 1984, с. 142]. Если при изменении структуры сети, пусть даже очень большой, в ней, в какой-то ее части, возникает один из этих графов (или оба), то двойственная сеть перестает существовать. Однако если в процессе дальнейшего изменения структуры эти графы меняют свою конфигурацию на любую другую, то двойственная сеть восстанавливается.

Эти графы представлены, соответственно, на рис. 1 и рис. 5. Каждый из них изображен как в традиционном представлении, так и в представлении, показывающим его непланарность в явном виде.

Сначала рассмотрим свойства сети, которая может быть двойственной к непланарному графу K₅, представленному на рис. 1.

том 21 № 3 (68), 2025, ст. 1

H

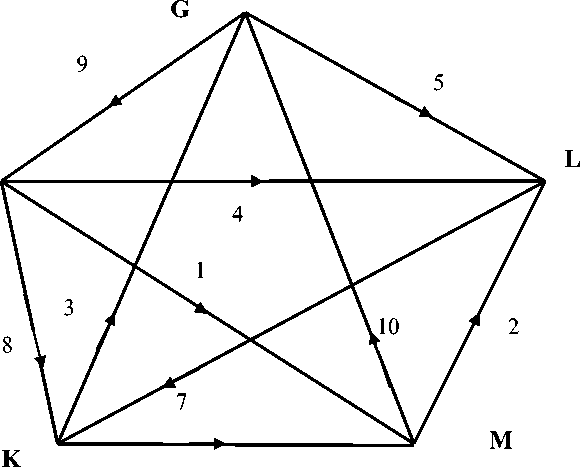
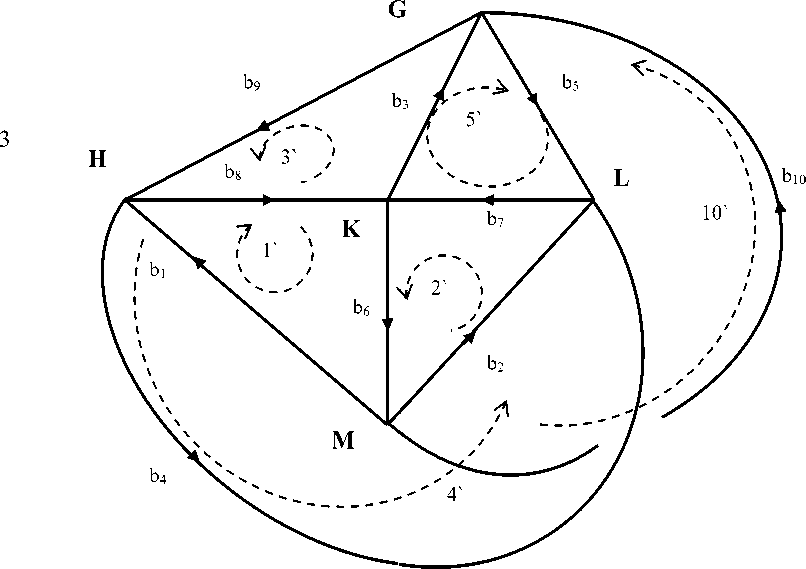
Рис. 1. Граф Ks в традиционном представлении, и его непланарность в явном виде

В данной сети на рис. 1 десять ветвей, n = 10 , узлов J = 5 , одна подсеть, s = 1 , следовательно, независимых разомкнутых путей j = 5 – 1 = 4 , независимых замкнутых путей, контуров m = n – j = 10 – 4 = 6 .

Матрица преобразования для независимых замкнутых и разомкнутых путей сети графа

К 5 , показанных пунктиром на рис. 1, имеет вид, С =

1		2	3	4	5	6	7	8	9	10
1	1	0	0	0	0	1	0	1	0	0
2	0	1	0	0	0	1	1	0	0	0
3	0	0	1	0	0	0	0	1	1	0
4	0	0	0	1	-1	0	0	0	1	0
5	0	0	0	0	1	0	1	-1	-1	0
С = 6	0	0	-1	0	0	1	0	0	0	1
7	0	0	0	0	0	0	1	0	0	0
8	0	0	0	0	0	0	0	1	0	0
9	0	0	0	0	0	0	0	0	1	0
10`	0	0	0	0	0	0	0	0	0	1

Матрица преобразования для двойственной сети такого непланарного графа не должна существовать. Однако оказалось, что она существует, и это ортогональная матрица, которая обычно соответствует двойственной сети A = С = С t ^-1 , она имеет вид:

	1	2	3	4	5	6	7	8	9	10
1	1	0	0	0	0	0	0	0	0	0
2	0	1	0	0	0	0	0	0	0	0
3	-1	-1	1	0	-1	1	0	0	0	0
4	0	0	0	1	0	0	0	0	0	0
С = С t -1      5	0	0	0	0	1	0	0	0	0	0
6	-1	-1	0	0	0	1	0	0	0	0
7	0	-1	0	-1	-1	0	1	0	0	0
8	0	1	-1	1	1	-1	0	1	0	0
9	1	1	-1	0	1	-1	0	0	1	0
10`	1	1	0	0	0	-1	0	0	0	1

По этой матрице можно пытаться построить двойственную сеть, которая не должна существовать для непланарного графа. При построении возникают противоречия, но в целом структура такой сети похожа на второй непланарный граф . Для данной матрицы два таких варианта показаны на рис. 2. Здесь наиболее интересен второй вариант, где контуры 7 и 10 соответствуют строкам 7 и 10 матрицы С . В строки 8 и 9 по построению входит путь через ветвь 3, которая должна иметь оба направления своей ориентации. В этом состоит противоречие в структуре сети и в базисе замкнутых путей. В базисе разомкнутых путей, как показано в матрице, пути 1, 2, 4, 5, 6 составляют «дерево» (остов) этого странного графа. А путь 3 включает ветви 1, 2, 4, 5, 6, и к ним ветвь 3, которая должна подключиться в узле A или в узле F , при этом второй узел должен «висеть» отдельно, иначе этот путь станет замкнутым.

В сети двойственной к сети на рис. 1, и показанной на рис. 2б, должно быть десять ветвей, n = 10, семь узлов, J = 7, одна подсеть, s = 1, следовательно, независимых разомкнутых путей j = 7 – 1 = 6, независимых замкнутых путей, контуров m = n – j = 10 – 6 = 4. Тогда сумма независимых замкнутых и разомкнутых путей постоянна и равна числу ветвей, т.е. десять.

Либо ветвь 3 должна быть отделена от сети, как это показано справа пунктиром, но также, как диктует матрица преобразования, входить в контуры 8 и 9, которые теперь состоят из двух петель. Зато ветвей десять, n = 10 , узлов J = 8 , две подсети, разомкнутых путей j = 8 – 2 = 6 , а контуров m = n – j = 10 – 6 = 4, т.е. требования топологии выполняются.

Оказывается, что хотя двойственный граф к непланарному графу и не существует (в наглядном представлении), но для него существует матрица преобразования, которую можно использовать, для расчета матрицы решения и потоков в сети. А, следовательно, использовать эту матрицу и соответствующий алгоритм для расчета компонент вектора потока энергии (воздействий и откликов) на ветвях сети с такой неизвестной, скрытой структурой.

Чтобы понять, как работает эта противоречивая топология, похожая по структуре на второй непланарный граф K 3.3 , произведём расчет сети, как электрической цепи, при заданных источниках, рассмотрим, как распределены токи и напряжения в ветвях. Формально это можно сделать, поскольку есть матрица С.

Расчет сети (цепи) тензорным методом .

Расчет как контурной, так и узловой сети сделаем по формулам тензорного анализа сетей, которые рассмотрены, например, в [10–12, 30–31]. Напомним формулы расчета сети тензорным методом с помощью матриц преобразования. Токи в независимых контурах связанной сети i^e' выражаются через токи в свободных ветвях i ^e по формуле:

ie = (Св- в)1 ie.(1)

Формулу преобразования напряжения получим, используя формулу преобразования тока:

e a i ^a = e a i^a' = e a' (C a' ^a ) -1t i ^a .

Тогда расчет напряжения при переходе от свободных ветвей к связанным ветвям:

ea= Caa ea(2)

Формула преобразования импеданса (метрический тензор) имеет вид:

Za-в' = Caa Zae Сввt(3)

том 21 № 3 (68), 2025, ст. 1

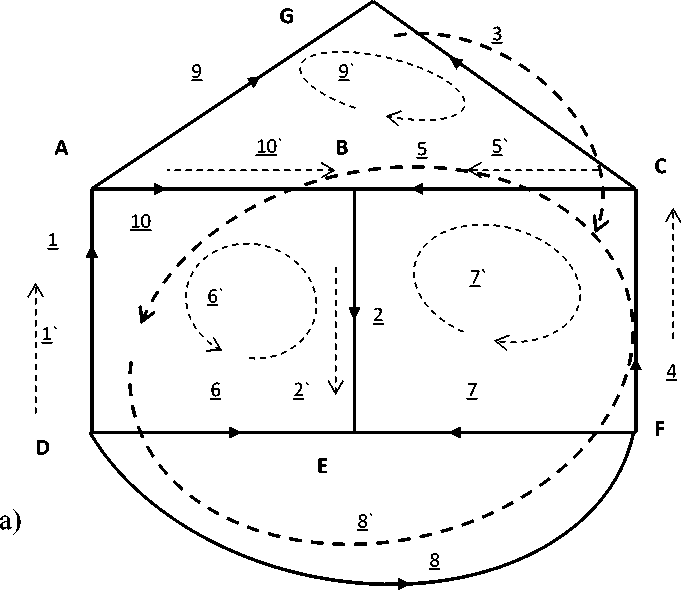
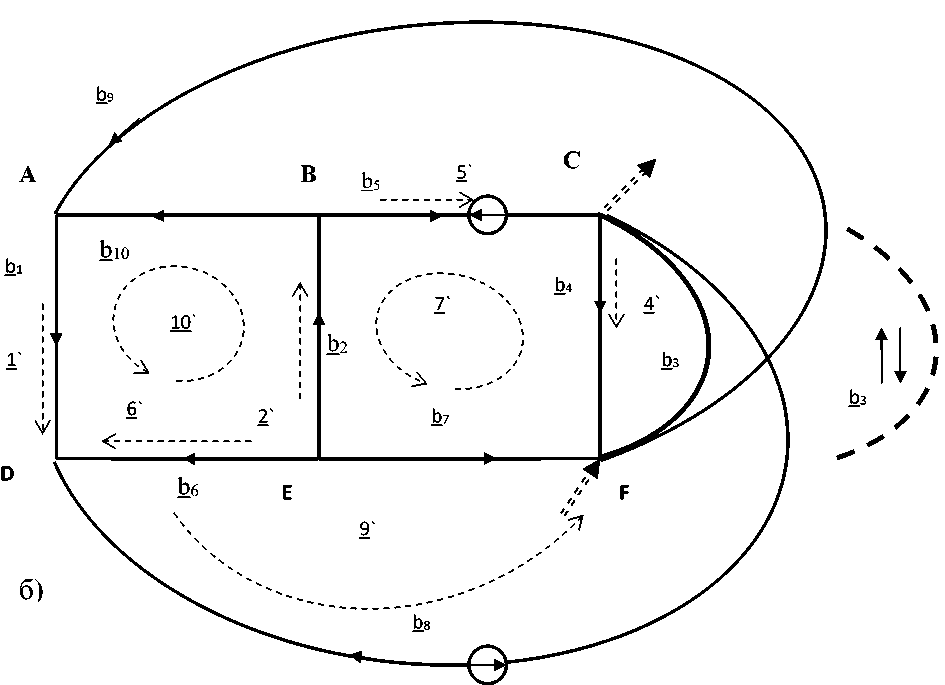
Рис. 2. Два варианта структуры сети, как бы двойственной к непланарному графу K 5 , похожи по структуре на второй непланарный граф K 3.3

Расчет цепи для источников напряжения . Пусть, для простоты, сопротивления ветвей, метрика, равны единицам. Заданы источники напряжения (ЭДС) e α , и матрица импедансов свободных ветвей Z ae = / , где I — единичная матрица. Надо найти токи в ветвях связанной цепи. В сети замкнутых свободных ветвей, где количество переменных совпадает с числом ветвей, расчет по формуле: i ^e = (Z ae )'¹ e a . В связанной сети число независимых контуров, вообще говоря, меньше числа ветвей. Получив матрицу преобразования путей, можно от заданных Z αβ и e α в простейшей сети перейти к величинам базиса путей в связанной сети с помощью формул (2) и (3). Затем по уравнению поведения связанной цепи получить токи в базисных замкнутых путях. Т.е. из e_a' = Z a ' e ' i^e' получим i^e' = (Za'e)'¹ e а ' и подставим сюда (2) и (3). Получим:

в = (^mC a'^a Z ae ^тС в^в t )¹ С'" e a                              (4)

Индекс m означает, что используется та часть матрицы преобразования, которая представляет замкнутые пути, базисные контуры в связанной цепи.

Токи в контурах представляют компоненты в базисных путях. По формуле (1) перейдем к измеримым величинам токов в ветвях связанной цепи, которые обозначим i ^β с . Тогда получим расчет откликов (токов) в ветвях по исходным источникам e α .

в = ^mC a ' ^a t 1^в' = ^mC a^a t C m C a'^a Z ae m C^ t )'¹ m C a'^a e a = Y c C a                    (5)

Выражение перед вектором e a обозначим Y c и назовем матрицей решения, умножение которой на e α сразу дает отклики в ветвях i ^β с . Отсюда получим напряжения на ветвях, e ^с α .

e ^ca = Z ae в = Z ae ^mC a'^at (^mC a^a Z ae ^тС в^в t )^{1 m}C a^a e a = Z ae Y c e a                      (6)

Проведем расчеты для сети графа К 5 , и двойственной сети, получим матрицы решения, которые умножим на вектор источников получим токи в ветвях.

Для сети графа К 5 матрица решения, источники и отклики имеют вид Y c e α = i ^β с :

	1      2      3      4      5      6      7      8      9     10											e		i β с
1 2 3 4 5 6 7 8 9 10`	3	-1	0	1	0	1	0	1	-1	-1	1 2 3 4 5 1/5    * 6 7 8 9 10`	1	=	1	(7) 1/5
	-1	3	0	-1	-1	1	1	0	0	-1		2		4
	0	0	3	0	1	-1	1	1	1	-1		0		1
	1	-1	0	3	-1	0	1	-1	1	0		0		-2
	0	-1	1	-1	3	0	1	0	-1	1		1		1
	1	1	-1	0	0	3	1	1	0	1		0		3
	0	1	1	1	1	1	3	-1	0	0		0		3
	1	0	1	-1	0	1	-1	3	1	0		0		1
	-1	0	1	1	-1	0	0	1	3	1		0		-2
	-1	-1	-1	0	1	1	0	0	1	3		0		-2

Элементы матрицы и откликов, токов в сетях, надо разделить на значение определителя, который в данном случае равен 5. Поскольку сопротивления ветвей равны единицам, то напряжения на ветвях численно равны токам в ветвях.

	Для	сети,	которая должна быть двойственной							к графу К 5 , также п			олучим отклики,
умножая матрицу решений 1      2      3    4					на вектор воздействий: 5     6     7     8     9					10		e α		i β с
1	2	1	0	-1	0	-1	0	-1	1	1	1	1	1	4
2	1	2	0	1	1	-1	-1	0	0	1	2	2	2	6
3	0	0	2	0	-1	1	-1	-1	-1	1	3	0	3	-1
4	-1	1	0	2	1	0	-1	1	-1	0	4	0	4	2	(8)
5	0	1	-1	1	2	0	-1	0	1	-1	5	1	5	4
6	-1	-1	1	0	0	2	-1	-1	0	-1	5   * 6	0	=    6	-3	5
7	0	-1	-1	-1	-1	-1	2	1	0	0	7	0	7	-3
8	-1	0	-1	1	0	-1	1	2	-1	0	8	0	8	-1
9	1	0	-1	-1	1	0	0	-1	2	-1	9	0	9	2
10`	1	1	1	0	-1	-1	0	0	-1	2	10`	0	10`	2

Элементы матрицы и откликов, токов в сетях, также надо разделить на значение определителя, который в данном случае равен 5. Поскольку сопротивления ветвей равны единицам, то напряжения на ветвях численно равны токам в ветвях.

Нетрудно проверить, что эти матрицы решения подчиняются, как и положено, инварианту двойственности, т.е. их сумма равна единичной матрице.

том 21 № 3 (68), 2025, ст. 1

b 1

e1 = 1

1'

b 9

A

i⁹ с = 2/5

i¹⁰ с = 2/5

B b ₅

b 10

10'

e2 = 2

b 2

i1 = 4/5

i⁶ с = -3/5

E

6     Ь б     2'

D

i7 = -3/5

b 8

i⁸ с = -1/5

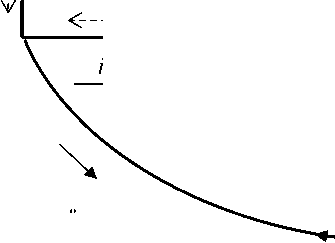
Рис. 3. Отклики и воздействия в контурной сети, как бы двойственной к графу K 5

i² с = 6/5

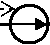
b 4

i4 = 2/5

4'

b 3

b 7

3/5

i5 = 4/5

e 0 ⁵ = 1

5'          C

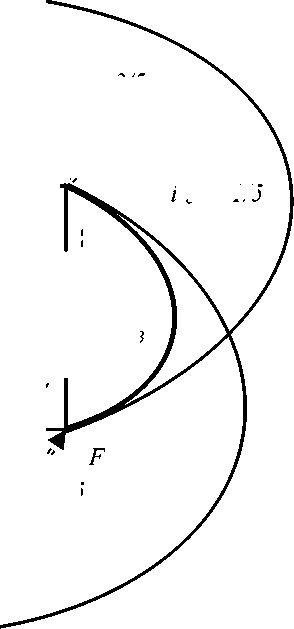
b 3

-3/5

i³ с = -1/5

I

Токи и напряжения в ветвях должны подчиняться законам Кирхгофа, что и является проверкой правильности решения. Для исходной сети непланарного графа легко проверить по сети на рис. 1, что сумма токов в узлах равна нулю, и сумма напряжений по каждому контуру равна нулю, т.е. законы Кирхгофа выполняются, расчет сделан правильно.

Проведем проверку законов Кирхгофа для второй сети, которая соответствует ортогональной матрице преобразования, и является попыткой стать двойственной сетью для непланарного графа. Значения откликов для этой сети показаны на рис. 3. Первый закон: сумма токов в узлах равна нулю. Токи, входящие в узел, со знаком плюс, выходящие – со знаком минус. Для двойственной сети непланарного графа на рис. 3 имеем, что Σ ^mi с ^α = 0 :

узел А : – ^mi с ¹ + ^mi с ⁹ + ^mi с ¹⁰ = (– 4 + 2 + 2)/5 = 0;

узел В : + ^mi с ² – ^mi с ⁵ – ^mi с ¹⁰ = (+ 6 – 4 – 2)/5 = 0;

узел С : – ^mi с ³ – ^mi с ⁴ + ^mi с ⁵ – ^mi с ⁸ = (– 1 – 2 + 4 + 1)/5 = +2/5; если ветвь три, b 3 , входит в С;

узел С : + ^mi с ³ – ^mi с ⁴ + ^mi с ⁵ – ^mi с ⁸ = (+ 1 – 2 + 4 + 1)/5 = +4/5; если ветвь три выходит из С;

узел С : – ^mi с ⁴ + ^mi с ⁵ – ^mi с ⁸ = (– 2 + 4 + 1)/5 = +3/5; если ветвь три, b 3 , вне сети;

узел D : + ^mi с ¹ + ^mi с ⁶ + ^mi с ⁸ = (+ 4 – 3 – 1)/5 = 0;

узел E : – ^mi с ² – ^mi с ⁶ – ^mi с ⁷ = (–6 + 3 + 3)/5 = 0;

узел F : + ^mi с ³ + ^mi с ⁴ + ^mi с ⁷ – ^mi с ⁹ = (– 1 + 2 – 3 – 2)/5 = –2/5; если ветвь три выходит из F ;

узел F : – ^mi с ³ + ^mi с ⁴ + ^mi с ⁷ – ^mi с ⁹ = (+ 1 + 2 – 3 – 2)/5 = –4/5; если ветвь три, b 3 , входит в F ;

узел F : + ^mi с ⁴ + ^mi с ⁷ – ^mi с ⁹ = (+ 2 – 3 – 2)/5 = –3/5; если ветвь три, b 3 , вне сети;

Топологически ветвь 3 должна быть отделена от сети, составлять отдельную подсеть. Можно допустить, что ветвь 3 выходит из узла С и входит в F , либо наоборот. Это диктует состав контуров, баланс напряжений в которых рассмотрен ниже. Во всех случаях в узлах С и F закон Кирхгофа не выполняется. Значения дисбаланса токов показывают, что часть тока уходит из узла С и приходит в узел F , как будто существует невидимое дополнение к этой сети. Эти внешние токи показаны на рисунке двойным пунктиром.

Второй закон Кирхгоффа: сумма напряжений в ветвях, ^me^с α , равна сумме воздействий (источников напряжения) ^me⁰ α в каждом контуре. Знаки определяются ориентацией напряжений на ветвях относительно направления контура. Для сети на рис. 3 это равенство имеет вид: Σ ^me^с α = Σ ^me⁰ α . Баланс напряжений в контурах получим следующий:

• •   контур 7`: – ^me^с 2 – ^me^с 4 – ^me^с 5 + ^me^с 7 = (– 6 – 2 – 4 – 3)/5 = –15 /5 = – 3 = – ^me⁰ 2 – ^me⁰ 5 ;

• •   контур 8`: + ^me^с 2 – ^me^с 3 + ^me^с 4 + ^me^с 5 – ^me^с 6 + ^me^с 8 = (+ 6 + 1 + 2 + 4 + 3 – 1)/5 = +15/5 =

= + ^me⁰ 2 + ^me⁰ 5 = + 2 + 1 = 3;

• •    контур 9': + ^те с1 + m e^c 2 - ^тесз + m e^c 5 - m e^c 6 + m e^c 9 = (4 + 6 +1 + 4 + 3 + 2)/5 = 20/5 = 4 =

= + ^me⁰ 1 + ^me⁰ 2 + ^me⁰ 5 = 1 + 2 + 1 = 4;

• •    контур 10`: + ^me^с 1 + ^me^с 2 – ^me^с 6 + ^me^с 10 = (+ 4 + 6 + 3 + 2)/5 = 15/5= ^me⁰ 1 + ^me⁰ 2 = 3.

Таким образом, во всех контурах закон Кирхгоффа выполняется, при условии, что ветвь три, b 3 , входит в эти контуры со своим знаком, хотя она должна быть вне сети .

Рассмотрим токи и напряжения в узловой сети при источниках тока, которые численно равны источникам напряжения в предыдущем примере. В силу инварианта двойственности, матрица решения узловой двойственной сети равна матрице решения данной контурной сети для непланарного графа, которая представлена в (7). Там же отклики в данной контурной сети численно равны откликам в узловой двойственной сети, если сопротивления ветвей равны 1 .

том 21 № 3 (68), 2025, ст. 1

I¹ 0 = 1

b 1

b 9

A

I⁹ с = -2/5

B

I¹⁰ с = Е 10 ^с = -2/5

b 5

b 10

I² 0 = 2

1'

I¹ с = 1/5

10'

b 2

E

Ь б       2'

D

I⁷ с = 3/5

Ь в

I² с = 4/5       _{b 7}

Рис. 4. Отклики и воздействия в узловой сети, как бы двойственной к графу K 5

I⁸ с = Е 8 ^с = 1/5

b 4

F

-3/5

I⁴ с = -2/5 b 3

5'          C

I⁵ 0 = 1

I⁵ с = Е 5 ^с = 1/5

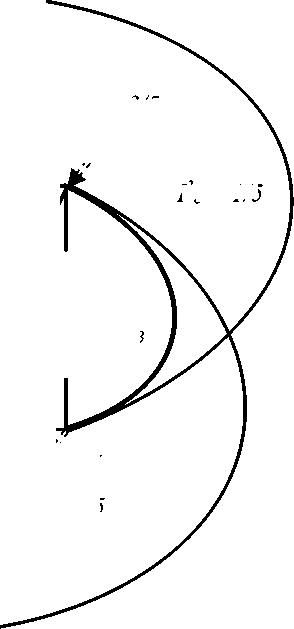
Ь з

3/5

I³ с = 1/5

1 /

Токи и напряжения в ветвях должны подчиняться законам Кирхгофа; это является проверкой правильности решения. Для исходной сети непланарного графа К 5 легко проверить по сети на рис. 1, что сумма токов в узлах равна нулю, и сумма напряжений по каждому контуру равна нулю, т.е. законы Кирхгофа выполняются, расчет сделан правильно.

Проведем проверку законов Кирхгофа для узловой сети, которая соответствует ортогональной матрице преобразования, и является попыткой стать двойственной сетью для непланарного графа. Значения откликов для этой сети показаны на рис. 4. Первый закон: сумма токов в узлах равна нулю, с учетом источников тока . Токи, входящие в узел, со знаком плюс, выходящие – со знаком минус. Для двойственной сети непланарного графа на рис. 4 имеем, что Σ ^jI с ^α = 0 :

узел А : – ^jI с ¹ – ^jI с ⁹ – ^jI с ¹⁰ + I¹ 0 = (– 1 – 2 – 2)/5 +1= 0 – выполняется;

узел В : + ^jI с ² – ^jI с ⁵ – ^jI с ¹⁰ = (+ 4 – 1 + 2)/5 = 5/5 = 1 ; + I² 0 – I⁵ 0 = 2 – 1 =1 – выполняется;

узел С : + ^jI с ³ – ^jI с ⁴ + ^jI с ⁵ – ^jI с ⁸ – I⁵ 0 = (+1 + 2 + 1 – 1)/5 – 1 = – 2/5; если ветвь b 3 входит в С;

узел С : – ^jI с ³ – ^jI с ⁴ + ^jI с ⁵ – ^jI с ⁸ – I⁵ 0 = ( – 1 + 2 + 1 – 1)/5 – 1 = – 4/5; если b 3 выходит из С;

узел С : – ^jI с ⁴ + ^jI с ⁵ – ^jI с ⁸ – I⁵ 0 = (+ 2 + 1 – 1)/5 – 1 = – 3/5; если ветвь b 3 вне сети;

узел D : + ^jI с ¹ + ^jI с ⁶ + ^jI с ⁸ – I¹ 0 = (+ 1 + 3 + 1)/5 – 1 = 0 – выполняется;

узел E : – ^jI с ² – ^jI с ⁶ – ^jI с ⁷ + I² 0 = (– 4 – 3 – 3)/5 + 2 = 0 – выполняется;

узел F : – ^jI с ³ + ^jI с ⁴ + ^jI с ⁷ – ^jI с ⁹ = (– 1 – 2 + 3 + 2)/5 = +2/5; если ветвь три выходит из F ;

узел F : + ^jI с ³ + ^jI с ⁴ + ^jI с ⁷ – ^jI с ⁹ = (+ 1 – 2 + 3 + 2)/5 = +4/5; если ветвь b 3 входит в F ;

узел F : + ^jI с ⁴ + ^jI с ⁷ – ^jI с ⁹ = (– 2 + 3 + 2)/5 = +3/5; если ветвь b 3 вне сети;

Топологически ветвь b 3 должна быть отделена от сети, как отдельная подсеть. Можно допустить, что эта ветвь выходит из узла С и входит в F , либо наоборот. Это диктует баланс напряжений в контурах. Также, как и в контурной сети, в узлах С и F закон Кирхгофа не выполняется. Значения дисбаланса токов показывают, что часть тока из узла С уходит, а в узел F приходит (в контурной сети наоборот), как будто существует невидимое дополнение к этой сети. Эти внешние токи показаны на рисунке двойным пунктиром.

Второй закон Кирхгоффа: сумма напряжений в ветвях, ^me^с α , равна сумме воздействий (источников напряжения) ^me⁰ α в каждом контуре. Знаки определяются ориентацией напряжений на ветвях относительно направления контура. Для сети на рис. 4 это равенство имеет вид: Σ ^me^с α = Σ ^me⁰ α . Баланс напряжений в контурах получим следующий:

• •   контур 7`: – ^jE^с 2 – ^jE^с 4 – ^jE^с 5 + ^jE^с 7 = (– 4 + 2 – 1 + 3)/5 = 0;

• •   контур 8`: + ^jE^с 2 – ^jE^с3 + ^jE^с 4 + ^jE^с 5 – ^jE^с 6 + ^jE^с 8 = (+ 4 – 1 – 2 + 1 – 3 + 1)/5 = 6 – 6 = 0;

• •   контур 9': + ^jE ^ci + ^jE^c₂ - ^jE^c3 + ^jE^c 5 - ^jE ^c6 + ^jE^c 9 = (1 + 4 — 1 +1 — 3 — 2)/5 = 6 - 6 = 0;

• •   контур 10`: + ^jE^с 1 + ^jE^с 2 – ^jE^с 6 + ^jE^с 10 = (+ 1 + 4 – 3 – 2)/5 = 0.

Получается, что для баланса напряжений ветвь b 3 должна входить и в контур 8, и в контур 9. При этом топологически ветвь b 3 должна быть вне сети. Т.е. токи в контурах должны «перескакивать» в эту ветвь, тогда закон Кирхгоффа выполняется.

Таким образом, для двойственной сети непланарного графа можно рассчитать токи и напряжения в контурном и узловом варианте, т.е. при внутренних и внешних воздействиях. Это указывает на то, что какая-то сеть существует. Однако баланс токов и напряжений в этой сети, похожей на второй непланарный граф K 3,3 , имеет некие скрытые связи, которые в данной структуре отобразить нельзя.

Можно также найти мощность, которая дополняет до полного инвариантного значения соответствующую величину вектора в сети, содержащей в своей структуре непланарный граф. Таким образом, все двойственные закономерности и инварианты продолжают выполняться и при возникновении непланарности, хотя наглядно представить при этом структуру двойственной сети в явном виде пока невозможно. Разрешение этого противоречия должно оказаться в чем-то другом, возможно, связанном с многомерными сетями.

Граф K 3,3 Рассмотрим свойства сети, двойственной ко второму непланарному графу K 3,3 .

Граф K 3,3 представлен на рис. 5, где он изображен как в традиционном представлении, так и в представлении, показывающим его непланарность в явном виде.

В сети графа K 3,3 на рис. 5 девять ветвей, n = 9 , узлов J = 6 , одна подсеть, s = 1 , следовательно, независимых разомкнутых путей j = 6 – 1 = 5 , независимых замкнутых путей, контуров m = n – j = 9 – 5 = 4 .

Матрица преобразования для независимых замкнутых и разомкнутых путей сети графа К 5 , показанных пунктиром на рис. 5, имеет вид, С (K 3,3 ) =

	1	2	3	4	5	6	7	8	9
1`	1	1	1	0	0	-1	0	0	0 m
2`	0	1	0	1	1	0	-1	0	0 m
3`	0	0	1	-1	-1	0	0	0	-1 m
4`	0	0	0	1	0	1	-1	-1	0 m
С = 5`	0	0	0	0	1	0	0	0	0 j
6`	0	0	0	0	0	1	0	0	0 j
7`	0	0	0	0	0	0	1	0	0 j
8`	0	0	0	0	0	0	0	1	0 j
9`	0	0	0	0	0	0	0	0	1 j

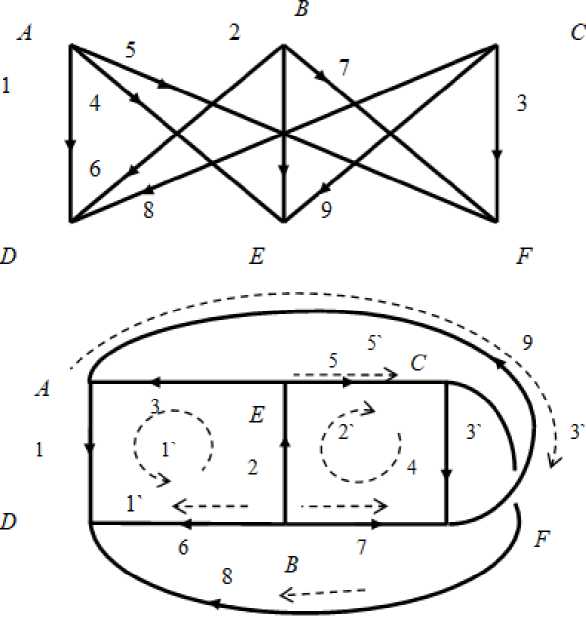
Рис. 5. Граф Кз,з в традиционном представлении, и в представлении, демонстрирующем его непланарность

том 21 № 3 (68), 2025, ст. 1

Матрица преобразования для двойственной сети такого непланарного графа не должна существовать. Однако оказалось, что она существует, и это ортогональная матрица, которая обычно соответствует двойственной сети A = С = Сt-1, она имеет вид:

	1	2	3	4	5	6	7	8	9
1`	1	0	0	0	0	0	0	0	0	j
2`	-1	1	0	0	0	0	0	0	0	j
3`	-1	0	1	0	0	0	0	0	0	j
4`	0	-1	1	1	0	0	0	0	0	j
С = С t -1      5`	0	-1	1	0	1	0	0	0	0	m
6`	1	1	-1	-1	0	1	0	0	0	m
7`	-1	0	1	1	0	0	1	0	0	m
8`	0	-1	1	1	0	0	0	1	0	m
9`	-1	0	1	0	0	0	0	0	1	m

По этой матрице можно пытаться построить двойственную сеть, которая не должна существовать для непланарного графа. При построении возникают противоречия, но в целом структура такой сети похожа на второй непланарный граф. Для данной матрицы два таких варианта показаны на рис. 6.

Для построения структуры сети используем строки 5 `– 9 `, которые соответствуют контурам, замкнутым путям. Например, путь 5 `показывает, что ветви 2 , 3 и 5 должны образовать замкнутый треугольник, в котором ветвь 2 ориентирована противоположно ветвям 3 и 5 . Аналогично соединяются ветви по остальным путям, каждый из которых должен добавлять хотя бы одну новую ветвь к уже охваченным ветвям. Признаком базиса замкнутых путей является то, что каждая ветвь вошла хотя бы в один контур. Разомкнутые пути описывают открытую часть сети, т.е. узлы, через которые происходит взаимодействие с внешним миром. Например, путь 1 ` соединяет узлы Н и М . Каждый следующий разомкнутый путь добавляет хотя бы один узел. Признаком базиса здесь является то, что каждый узел вошел хотя бы в один разомкнутый путь.

Построенная по этой матрице соответствующая сеть представлена на рис. 6.

том 21 № 3 (68), 2025, ст. 1

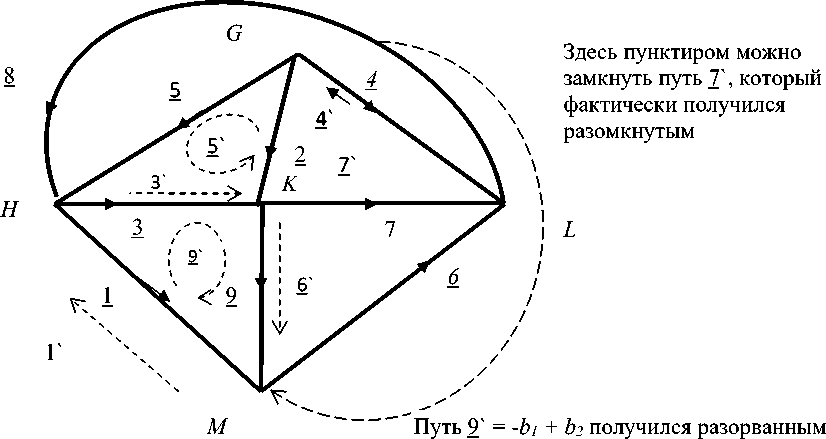
Рис. 6. Граф, который соответствует ортогональной матрице к матрице путей графа К 3,3 похож на граф К 5 , но ему не хватает одной ветви для замыкания пути 7 `

Можно заметить, что хотя для этой сети, граф (структура) которой не должна существовать, матрица преобразования существует и имеет вполне определенный вид. Строки в этой матрице перечисляют ветви, входящие в независимые замкнутые и разомкнутые (базисные) пути двойственной сети. Соединяя ветви в той последовательности и с той ориентацией, которая указана в строках ортогональной матрицы преобразования, можно попытаться построить структуру двойственной сети в явном виде. Сеть, которая показана на рис. 6, построена так, как указывает состав ветвей в путях этой матрицы. Граф этой сети, которая соответствует ортогональной матрице к матрице путей графа К 3,3 похож на граф К 5 .

Противоречия состоят в том, что для замыкания пути 7 ` не хватает одной ветви. Дело в том, что один замкнутый путь, в соответствии с ортогональной матрицей преобразования (а она, как известно, является единственной), оказался разомкнутым. Этот путь 7 `состоит из ветвей 1 , 3 , 4 и 7 . Для того чтобы он стал замкнутым, нужна еще одна ветвь, которая бы замыкала узлы G и М . Если такую ветвь добавить, то, как нетрудно видеть, двойственная сеть к графу К 3,3 превратится в сеть, которая соответствует графу К 5 . Эта недостающая для замыкания пути 7 ` ветвь показана пунктиром в правой части рисунка. Кроме того, ветвь 4 в путях 6 ` и 7 ` должна иметь разные ориентации.

В сети двойственной к сети на рис. 5, и показанной на рис. 6, должно быть девять ветвей, n = 9, пять узлов, J = 5, одна подсеть, s = 1, следовательно, независимых разомкнутых путей имеем j = J – s =5 – 1 = 4, независимых замкнутых путей, контуров m = n – j = 9 – 4 =

том 21 № 3 (68), 2025, ст. 1

• 5 . Тогда сумма независимых замкнутых и разомкнутых путей постоянна и равна числу ветвей, т.е. девять. Таким образом. требования двойственности сетей выполняются.

Хотя двойственный граф к непланарному графу и не существует (в наглядном представлении), но для него существует матрица преобразования, которую можно использовать, для расчета матрицы решения и потоков в сети. А, следовательно, использовать эту матрицу и соответствующий алгоритм для расчета компонент вектора потока энергии (воздействий и откликов) на ветвях сети с такой неизвестной, скрытой структурой.

Проведем расчеты для сети графа К 3,3 , и двойственной сети по формулам 1-6, получим матрицы решения, которые умножим на вектор источников получим токи в ветвях.

Для сети графа К 3,3 матрица решения, источники и отклики имеют вид Y c e α = i ^β с :

	1	2	3	4	5	6	7	8	9	e α		i β с
1	4,0	1,0	2,0	1,0	-1,0	-2,0	1,0	-2,0	2,0	1	1	1	5
2	1,0	4,0	2,0	1,0	2,0	-2,0	-2,0	1,0	-1,0	2	2	2	11
3	2,0	2,0	4,0	-1,0	-2,0	-1,0	-1,0	-1,0	-2,0	3	0	3	4
4	1,0	1,0	-1,0	4,0	2,0	1,0	-2,0	-2,0	2,0	4	0	4	5
5	-1,0	2,0	-2,0	2,0	4,0	-1,0	-1,0	2,0	1,0	1/9   * 5	1	= 5	7	1/9
6	-2,0	-2,0	-1,0	1,0	-1,0	4,0	-2,0	-2,0	-1,0	6	0	6	-7
7	1,0	-2,0	-1,0	-2,0	-1,0	-2,0	4,0	1,0	2,0	7	0	7	-4
8	-2,0	1,0	-1,0	-2,0	2,0	-2,0	1,0	4,0	-1,0	8	0	8	2
9	2,0	-1,0	-2,0	2,0	1,0	-1,0	2,0	-1,0	4,0	9	0	9	1

Элементы матрицы и откликов, токов в ветвях, надо разделить на значение определителя, который в данном случае равен 9. Поскольку сопротивления ветвей равны единицам, то напряжения на ветвях численно равны токам в ветвях.

Для сети, которая должна быть двойственной к графу К 3,3 , также можем получить отклики, умножая матрицу решений на вектор воздействий. Можно использовать инвариант двойственности , и получить отклики, как в узловой сети, так и в контурной двойственной сети по формуле i ^β с = i ^β 0 - i ^β с =

	1	2	3	4	5	6	7	8	9
i β с =	4	7	-4	-5	2	7	4	-2	-1	1/9

Элементы матрицы и откликов, токов в сетях, также надо разделить на значение определителя, который в данном случае равен 9. Поскольку сопротивления ветвей равны единицам, то напряжения на ветвях численно равны токам в ветвях.

Токи и напряжения в ветвях должны подчиняться законам Кирхгофа, что и является проверкой правильности решения. Для исходной сети непланарного графа легко проверить по

том 21 № 3 (68), 2025, ст. 1

сети на рис. 6, что сумма токов в узлах равна нулю, и сумма напряжений по каждому контуру равна нулю, т.е. законы Кирхгофа выполняются, расчет сделан правильно.

Проведем проверку законов Кирхгофа для второй сети, которая соответствует ортогональной матрице преобразования, и является попыткой стать двойственной сетью для непланарного графа. Значения для этой сети откликов (численно равных друг другу токов и напряжений) показаны на рис. 7. Первый закон Кирхгофа состоит в том, что сумма токов в узлах равна нулю.

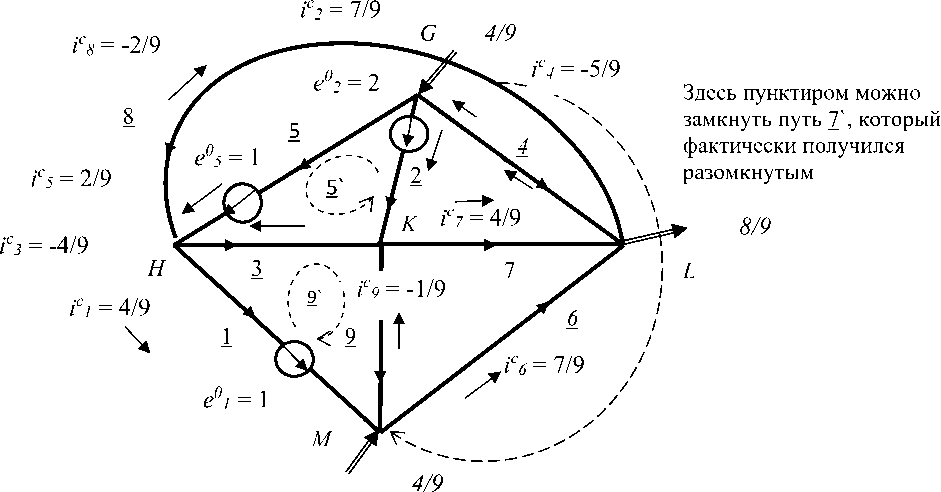
Рис. 7. Отклики, токи и напряжения, а также воздействия в контурной сети, как бы двойственной к графу К 3,3

Токи, входящие в узел, со знаком плюс, выходящие – со знаком минус. Для двойственной сети непланарного графа на рис. 7 имеем, что Σ ^mi с ^α = 0 :

узел G : – ^mi с ² – ^mi с ⁴ – ^mi с ⁵ = (– 7 – 2 + 5)/9 = – 4/9;

узел H : – ^mi с ¹ – ^mi с ³ + ^mi с ⁵ + ^mi с ⁸ = (– 4 + 4 + 2 – 2)/9 = 0;

узел K : + ^mi с ² + ^mi с ³ – ^mi с ⁷– ^mi с ⁹ = (– 4 + 7 + 1 – 4)/9 = 0;

узел L : + ^mi с ⁴ + ^mi с ⁶ + ^mi с ⁷ – ^mi с ⁸ = (– 5 + 4 + 7 + 2)/9 = + 8/9;

узел M : + ^mi с ¹ – ^mi с ⁶ + ^mi с ⁹ = (+ 4 – 1 – 7)/9 = – 4/9.

В узлах G, L и M закон Кирхгофа не выполняется. Значения дисбаланса токов показывают, что часть тока уходит из узла L и приходит в узлы G и M , как будто существует невидимое дополнение к этой сети. Причем ток из узла L равен сумме токов, входящих в узлы G и M. Эти внешние токи показаны на рисунке двойным пунктиром.

Второй закон Кирхгоффа: сумма напряжений в ветвях, ^me^с α , равна сумме воздействий (источников напряжения) ^me⁰ α в каждом контуре. Знаки определяются ориентацией напряжений на ветвях относительно направления контура. Для сети на рис. 7 это равенство имеет вид: Σ ^me^с α = Σ ^me⁰ α . Баланс напряжений в контурах получим следующий:

• •   контур 5`: – ^me^с 2 + ^me^с 3 + ^me^с 5 = ( – 7 – 4 + 2)/9 = –9/9 = ^me⁰ 5 = 1.

• •   контур 6`: + ^me^с 1 + ^me^с 2 – ^m e^с 3 – ^me^с 4 +^me^с 6 = (+4 + 7 + 4 + 5 + 7)/9 = 27/9 = ^me⁰ 1 + ^me⁰ 2 = 3.

• •   контур 7`: – ^me^с 1 + ^me^с 3 + ^me^с 4 + ^me^с 7 = (– 4 – 4 – 5 + 4)/9 = –9 /9 = – ^me⁰ 1 = 1;

• •   контур 8`: – ^me^с 2 + ^me^с 3 + ^me^с 4 + ^me^с 8 = (– 7 – 4 – 5 – 2)/9 = +18/9 = + ^me⁰ 2 = + 2;

• •   контур 9`: – ^me^с 1 + ^me^с 3 + ^me^с 9 = ( – 4 – 4 – 1)/9 = – 9/9 = – 1 =+ ^me⁰ 1 = 1.

Таким образом, во всех контурах закон Кирхгоффа выполняется.

Рассмотрим токи и напряжения в узловой сети при источниках тока, которые численно равны источникам напряжения в предыдущем примере. В силу инварианта двойственности, матрица решения узловой двойственной сети равна матрице решения данной контурной сети для непланарного графа. Отклики в данной контурной сети численно равны откликам в узловой двойственной сети, если сопротивления ветвей равны 1 .

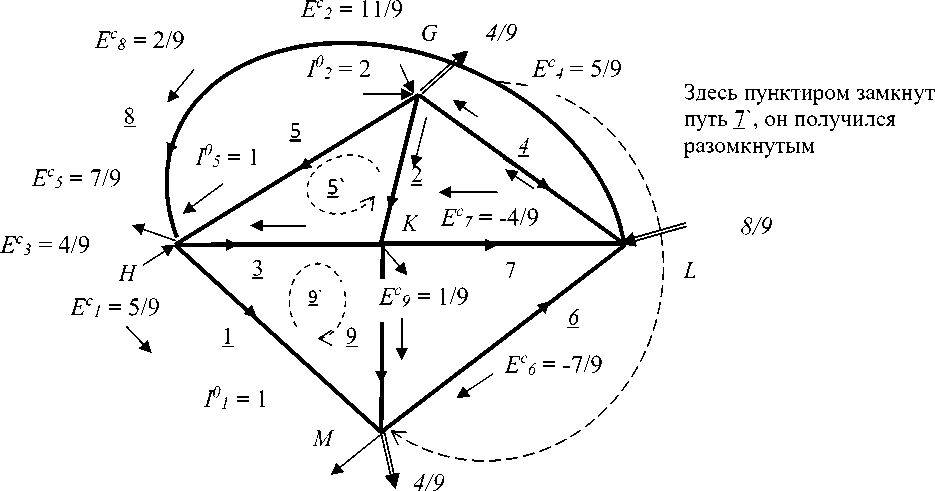
Рис. 8. Отклики (токи и напряжения в ветвях) и воздействия, узловые токи, в узловой сети, как бы двойственной к графу К з,з

Токи и напряжения в узловой сети, которая должны быть двойственной к графу К 3,3

1       2       3       4       5       6       7       8       9

j _{I с} α ₌ j _{E с α}

5

11

4

5

7

-7

-4

2

1

1/9

Токи и напряжения в ветвях должны подчиняться законам Кирхгофа; это является проверкой правильности решения. Для исходной сети непланарного графа К 3,3 легко проверить по сети, что сумма токов в узлах равна нулю, и сумма напряжений по каждому контуру равна нулю, т.е. законы Кирхгофа выполняются.

Проведем проверку законов Кирхгофа для узловой сети, которая соответствует ортогональной матрице преобразования, и является должна быть двойственной сетью для непланарного графа. Значения откликов для этой сети показаны на рис. 8. Первый закон: сумма токов в узлах равна нулю, с учетом источников тока . Токи, входящие в узел, со знаком плюс, выходящие – со знаком минус. Для сети должно быть, что Σ ^jI с ^α = 0 :

узел G : – ^jI с ² – ^jI с ⁴ – ^jI с ⁵ = (– 11 – 7 – 5)/9 =– 23/9. Это не равно сумме источников в узле, равной + ^jI 0 ² + ^jI 0 ⁵ = 1 + 2 = 3 ; для баланса из узла должен выходить ток –4/9 узел H : – ^jI с ¹ – ^jI с ³ + ^jI с ⁵ + ^jI с ⁸ + I¹ 0 – I⁵ 0 = ( – 5 – 4 + 7 + 2 + 1 – 1) /9 = 0 – выполняется;

узел K : + ^jI с ² + ^jI с ³ – ^jI с ⁷ – ^jI с ⁹ – ^jI 0 ² = (+ 11 + 4 + 4 – 1)/9 – 2 = 18/9 – 2 = 0 – выполняется;

узел L : + ^jI с ⁴ + ^jI с ⁶ + ^jI с ⁷ – ^jI с ⁸ = (+5 – 7 – 4 – 2)/9 – 1 = – 8/9 – не выполняется, в контурной сети здесь получилось + 8/9;

узел M : + ^jI с ¹ – ^jI с ⁶ – ^jI с ⁹ – I¹ 0 = (+ 5 + 7 + 1)/9 – 1 = +4/9 – не выполняется, из узла должен выходить ток 4/9, в контурной сети здесь получилось должен входить ток – 4/9.

Также, как и в контурной сети, в узлах G, L и M закон Кирхгофа не выполняется. Значения дисбаланса токов в этих узлах показывают, что они имеют противоположные знаки, чем в контурной сети, как будто существует невидимое дополнение к этой сети. Эти внешние токи показаны на рисунке двойным пунктиром.

Второй закон Кирхгоффа: сумма напряжений в ветвях, ^jE^с α , равна сумме воздействий (источников напряжения) ^jE⁰ α в каждом контуре. Знаки определяются ориентацией напряжений на ветвях относительно направления контура. Для сети на рис. 8 это равенство имеет вид: Σ ^jE^с α = Σ ^jE⁰ α . Баланс напряжений в контурах получим следующий:

• •   контур 5`: – ^jE^с 2 + ^jE^с 3 + ^jE^с 5 = (– 11 + 4 + 7)/9 = 0.

• •   контур 6`: + ^jE^с 1 + ^jE^с 2 – ^jE^с 3 –^jE^с 4 + ^jE^с 6 = (+ 5 + 11 – 4 – 5 – 7)/9 = 0.

• •   контур 7`: – ^jE^с 1 + ^jE^с 3 + ^jE^с 4 + ^jE^с 7 = (– 5 + 4 + 5 – 4)/9 = 0;

• •   контур 8`: – ^jE^с 2 – ^jE^с 3 + ^jE^с 4 + ^jE^с 8 = (– 11 + 4 + 5 + 2)/9 = 11 – 11 = 0;

• •   контур 9`: – ^jE^с 1 + ^jE^с 3 + ^jE^с 9 = (– 5 + 4 + 1)/9 = 0;

Т.е. по всем контурам выполняется второй закон Кирхгоффа.

Обсуждение

Для каждого непланарного графа существует решение для сети, каждая из которых похожа на второй непланарный граф. Для двойственной сети каждого непланарного графа можно рассчитать токи и напряжения в контурном и узловом варианте, т.е. при внутренних и внешних воздействиях. Это указывает на то, что какая-то сеть существует, и в ней протекают потоки как в контурной сети, так и в узловой сети.

Однако баланс токов и напряжений в этой сети, похожей на второй непланарный граф K 5 , имеет некие скрытые связи, которые в данной структуре отобразить нельзя. Можно предположить, что в этой «точке структурной сингулярности» двойственные к непланарным графам как-то связаны между собой.

Заключение

Полученные решения для двойственных сетей, вместе с матрицами преобразования двойственных сетей использовали для того, чтобы попытаться понять, как устроена структура двойственного графа к непланарному графу, который не должен существовать. Получается, что два непланарных графа, K 3,3 и K 5 , по своей структуре похожи на двойственные друг к другу, но весьма необычным образом.

Возможно, что одна ветвь принадлежит при двойственном переходе одновременно к двум графам, что может играть определенную роль для установления границы между двумя пространствами.

Исследование противоречий инварианта мощности в тензорном методе, показавшем практическую применимость, показало, что надо искать решение «в другой плоскости», в соответствии с диалектикой. Для решения проблемы инварианта мощности следовало провести поиск закономерности изменения рассеиваемой мощности при изменении структуры, в частности, при изменении соединения ветвей в электрической цепи.

Найденная закономерность постоянства мощности при изменении структуры двойственных сетей не следует из ранее известных теоретических положений и экспериментальных фактов. Это самостоятельная физическая закономерность, которая определяется свойствами структуры и проявляется при прохождении потока энергии в электрической цепи.

Для решения противоречий, связанных с двойственными сетями и непланарными графами также нужен выход на какое-то новое «измерение», новое знание. Сама проблема, как показал автор, на вид понятна, проста и наглядна, но решения на сегодня не имеет. Это одна из наиболее фундаментальных проблем, требующих исследования. Можно ожидать, что ее решение даст путь к открытию новых свойств нашего мира, связанных с законами структуры в основании технических, экономических, биологических систем.