Непрерывные аппроксимации решения задачи "выполнимость" применительно к криптографическому анализу асимметричных шифров

Область науки, носящая имя криптографический анализ, в настоящее время имеет громадное практическое значение, так как гарантировано стойкие алгоритмы шифрования являются основой надежности современных систем телекоммуникаций и систем финансовых взаиморасчетов. С теоретической стороны, прогресс в области криптографического анализа сопровождается бурным развитием смежных областей математики: алгебры, теории чисел, дискретной математики.

Основным подходом проверки криптографической стойкости асимметричных шифров в настоящее время являются алгоритмы числового решета в поле чисел общего вида [12] и различные модификации алгоритмов ρ- и λ- Полларда, основывающиеся на детерминированном случайном блуждании по группе [11]. Сообщения, появляющиеся время от времени, лишь подтверждают стойкость известных алгоритмов. Например, для факторизации чисел «рабочих» размерностей (~1000 бит) требуется задействовать на несколько месяцев вычислительные мощности кластеров из самых верхних позиций списка Топ-500. То есть увеличение длины ключа в полтора или два раза решает вопрос о криптостойкости принципиально.

Совершенно новой альтернативой алгебраическому подходу является так называемый логический криптоанализ, когда криптографический алгоритм рассматривается как программа для машины Тьюринга и подстановка открытого и шифрованного текстов в эту программу естественным образом приводит к задаче ВЫПОЛНИМОСТЬ для КНФ[9]. Часть выполняющего набора является ключом алгоритма. Идея такого подхода была впервые предложена в работе [8]. Как показал опыт, применение переборных алгоритмов, с частью из которых можно ознакомиться в обзоре [10], сталкивается с принципиальными трудностями, связанными с размерностями задач. Естественно, возникает идея перехода к непрерывным моделям, когда поиск выполнимого набора для КНФ осуществляется как поиск минимума ассоциированного с КНФ функционала. Впервые эта идея была реализована в работах [3, 4]. Были предприняты попытки связать задачу минимизации с некой физической моделью, так, в работе [5] была предложена модель химической кинетики, а в работе [6] - гравитационная аналогия. Обратим внимание на то, что имеется принципиальное отличие непрерывных методов от переборных алгоритмов локального поиска, - сдвиг по антиградиенту происходит по всем переменным сразу. Также, априори известно, что глобальный минимум функционала единственен и в случае, когда локальных минимумов и других особых точек нет, минимизация происходит эффективно. С другой стороны, нет необходимости в том, чтобы «точно» определить все биты ключа. Достаточно той информации, что набор бит, или ключа, или множества бит, однозначно определяющего ключ, совпадает с точным решением с вероятностью значимо большей, чем 0,5. А в результате применения итерационных методов можно надеяться на то, что мы сможем «подобраться» к такой окрестности достаточно близко. Таким образом, проверка известных в настоящее время алгоритмов на стойкость к поиску глобального экстремума является новым и необходимым тестом.

Можно надеяться, что привлечение богатого арсенала вычислительной математики к данному классу задач и синтез с методами, присущими для дискретного подхода, позволит получить новые результаты и уточнить пределы применимости существующих в настоящее время криптографических алгоритмов.

Переход от КНФ к ассоциированным функционалам

Пусть дана КНФ на множестве булевых переменных y ∈ B^N {0,1} :

M

L ( У ) = a C i ( y ), где i = 1

M

C i ( У ) = V l ( y j ), l ( y j ) = y j или y, . j e {1... N } ^J             J J J

Введем вещественные переменные x e R ⁿ [0,1] такие, что x соответствует булевой переменной y , а (1 - x )² соответствует ее отрицанию.

Рассмотрим переход от задачи ВЫПОЛНИМОСТЬ (SAT) к задаче поиска глобального минимума функционала вида (1):

M min F(x)=e Ci (x), где xe Rn [0,1]         “1

C i (x ) = fl Q , y ( х , ), где                         (1)

j = 1

x 2 ,      если y j - e c i ( x )

Q i,j ( x j ) = I (1 — x , ) , если y j - e C i ( x ).

1,

иначе

Суммирование ведется по всем M конъюнктам ДНФ, эквивалентной исходной КНФ. Переход от булевой формулы к вещественной основан на использовании соответствия:

^yi ^{V y}j ^ ^xi + x j

< y i . Л y j ^ x²x²   , где { y i . ^e B , x i ^e R ^} .

, y      - (1 - x i .)

Легко заметить, что min F ( x ) = 0 соответст- x e R ⁿ [0,1]

вует достижению значения ИСТИНА на исходной КНФ.

Дифференцируя функционал по всем переменным x_i , получим систему уравнений:

E z ² z 2 ... • x i = E z 2 z 2.. , i = 1,2,.. P , где §eE             £еЛ

[ x i ,        если y i e c i ( y )

zi = 1

[ (1 - x i ), если y i e c i ( y )

E= { ^ , i e^ : x i e c i ⁽ x ) }

Л = { ^ , i e^ : x i e c i ( x ) } .

Как показано в [1], применение метода Ньютона к решению данного уравнения неэффективно, т.к. решение принадлежит ядру производного оператора. Как альтернатива был предложен метод последовательных приближений с «инерцией»:

K

EE “ ^ x i ( t — P ) 2 x , ( t - k ) 2

p = 0 ^e =

• x k ( t + 1) =

= E x j ( t ) x ^ ²( t )~ A • x i ( t + 1) = B                  (3)

^ел              def

E a p = 1, a p e R [0,1].

p = 1

Имеется в виду, что итерации проводятся для вещественных чисел, а итоговый или промежуточный вектор проектируется на B^N {0,1}, и уже на булевом векторе проверяется ВЫПОЛНИМОСТЬ. Ниже описаны различные модификации метода последовательных приближений с «инерцией» и показаны способы повышения эффективности алгоритма.

Гибридизация алгоритма

Исходная КНФ преобразуется методом резолюции [7], это позволяет получить КНФ с меньшим количеством дизъюнктов и литералов, эквивалентную исходной.

Два дизъюнкта разрешимы относительно бинарной резолюции (бинарно-разрешимы), если они совпадают хотя бы по одной переменной, которая входит в один дизъюнкт с отрицанием, а в другой - без. Бинарно разрешимые дизъюнкты имеют вид:

x V P, x V Q.

Резольвентой бинарно-разрешимых дизъюнктов (бинарной резольвентой) называется дизъюнкт P V Q. Все возможные бинарные резольвенты с помощью операции дизъюнкции добавляются к КНФ и используются для вычисления других резольвент. Процедура ограничивается глубиной рекурсии 1. Дублирующие конъюнкты и тавтологии удаляются. Вычислительная сложность процедуры O(n⋅log(n)).

Основная процедура состоит из последовательных итераций, которые совмещают метод последовательных приближений и сдвиг по антиградиенту, т.к. правая часть (2) - это хотя и градиент исходного функционала, но решения (2) - это всего лишь стационарные точки функционала. Например, если генерировать КНФ по заданной строке бит, случайно строя скобки, так, чтобы строка бит была решающим набором итоговой КНФ, то представительство литералов и их отрицаний будет одинаковым. Это означает, что ассоциированный функционал имеет «квазистационарную» точку с координатами 0,5 для каждой переменной, т.к. A_i ~ 2 B_i . В случае же, когда представительство литералов неравное, то подобные «квазистационарные» точки могут быть произвольными. Например, генерируя случайную систему уравнений и сводя задачу к поиску решающего набора КНФ, мы получаем уже существенно неравное представительство литералов. В этом случае квази-стационарным точкам будут соответствовать решения неопределенных систем, получаемые из исходной системы исключением всего нескольких уравнений. Число таких точек растет экспоненциально с ростом размерности системы, и итерационная процедура поиска стационарной точки, интересующей нас как отвечающей точке минимума, практически перестает сходиться, что и подтверждается экспериментально.

Итерация состоит из двух блоков. Первый блок определяется формулой (3), используется схема Зейделя. Второй блок – реализация сдвига по антиградиенту: x ( t + 1) = 2 • x ( t ) - B / A [1].

При приближении к решению скорость сходимости может сильно уменьшаться, одна из возможных причин этого в том, что траектория, образованная последовательными приближениями, «зацикливается» в областях локальных минимумов функционала. Метод смены траектории позволяет выйти из локального минимума с помощью формирования нового вектора приближения, который бы обладал свойствами не худшими, чем текущий вектор приближения, но позволял бы продолжить поиск решения [1].

Распараллеливание алгоритма

Гибридный алгоритм допускает целый набор способов распараллеливания, приведем один из них.

ДНФ, эквивалентная исходной КНФ, делится на две независимые части (подформулы). Векторы решений для подформул определяют точки в n -мерном пространстве. Между полученными точками проводится отрезок прямой. «Двигаясь» по этой прямой с некоторым шагом l, можно вычислить вектора { x_l } по формуле

A IХц - x^ I , xli = minXu, x2i) +-----------l .

k

Вектор {xl}, при котором значение функционала (1) минимально, становится новым начальным набором приближений для итерационной процедуры, которая запускается для функционала, ассоциированного со всей формулой.

Описанная процедура позволяет максимально приблизиться к решению. В формуле остаётся до 2% дизъюнктов невыполнимыми. При этом около 2,5% переменных остаются неопределенными, то есть независимо от того, какое значение они будут принимать, выполнимые скобки будут по-прежнему принимать значение ИСТИНА.

Тестирование метода

Для тестирования разработанного алгоритма использовалось несколько типов примеров: тесты с соревнований решателей SAT 2005 года [13], тесты специализированной библиотеки SATLib [14], тесты, сформированные для задачи факторизации, тесты больших размерностей, сформированные псевдослучайным заполнением дизъюнктов.

Результаты тестирования однопроцессорной реализации алгоритма для тестовых задач различных серий из библиотеки SATLib представлены в табл.1.

Результаты тестирования параллельной версии алгоритма на задачах из библиотеки SATLib и задачах, представленных на соревнованиях решателей SAT 2005 года, приведены в табл.2.

Таблица 1. Результаты численных экспериментов для тестовых задач из SATLib

Наименование теста	Количество литералов (N)	Количество дизъюнктов (M)	Число тестов	% решенных тестов	Максимальное число итераций
Backbone-minimal Sub-instances (формулы с минимальным хребтом), 3-SAT
RTI	100	429	500	98,6	19988
BMS	100	<429	500	79,8	29831
Controlled Backbone Size Instances (формулы с хребтом фикси			рованного размера, b), 3-SAT
CBS_b10	100	403	1000	100	38972
CBS_b10	100	449	1000	100	38880
CBS_b90	100	449	1000	98	29738
Uniform Random 3-SAT (UF)
UF20-91	20	91	1000	100	448
UF250-1065	250	1065	100	98	9731
Задачи, ассоциированные с оптимизационным вариантом задачи «раскраска графа»
FLAT30-60	90	300	100	100	4317

Таблица 2. Результаты численных экспериментов параллельного алгоритма для тестовых задач из SATLib

Наименование теста	Количество литералов (N)	Количество дизъюнктов (M)	% решенных тестов	Число итераций необходимое для решения:
				Части КНФ	Всей КНФ
RTI	100	429	100	10	14
BMS	100	<429	100	7	14
sat05-1663	2000	8400	99	20	200
sat05-1676	4000	16800	99	20	200
sat05-1656	12000	50400	99	20	200
UF20-91	20	91	100	10	14
UF250-1065	250	1065	100	20	21

Применение метода к криптографическому анализу асимметричных шифров, сводка результатов, выводы

Была исследована схема применения метода для решения задач криптографического анализа. Конъюнктивные нормальные формы, ассоциированные с задачами факторизации, дискретного логарифмирования и дискретного логарифмирования на эллиптической кривой рассматриваются в работах [2]. Оценка роста числа дизъюнктов и скобок в зависимости от размерности задачи ( N ) дает нам величину CN ², C ≈ 10 для задачи факторизации и C ₁ N ³, C ₂ N ³, C ₁ ≈ 100, C ₂ ≈ 1000 для задач дискретного логарифмирования и дискретного логарифмирования на эллиптической кривой. Метод резолюций в применении к КНФ для факторизации уменьшает число дизъюнктов более чем в 2 раза, а в применении к задаче дискретного логарифмирования позволяет уменьшить число переменных на два порядка, что приводит к относительно приемлемым цифрам для массива данных.

В рамках работы проводились исследования близости формируемых методом векторов приближений к вектору решения для задач факторизации больших размерностей. В качестве исходного материала для тестирования были выбраны по 10 независимых примеров размерностей 1024, 2048, 3072 бит. На каждой итерации метода последовательных приближений с «инерцией» проводилось сравнение компонент вектора приближений с соответствующими компонентами вектора решений с целью подсчета числа совпадающих компонент (битов). При этом производилось по 10 стартов со случайно сформированного вектора начального приближения. На рис. 1 показано поведение процентного отношения верно сформированных бит на соответствую-

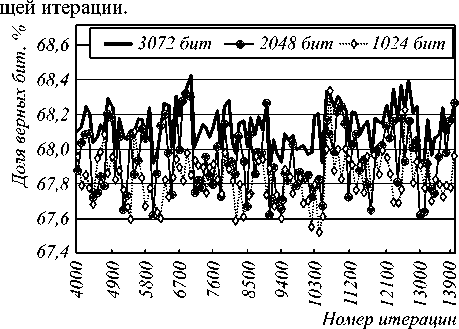
Рис. 1. Процент совпадающих (верных) бит вектора приближения и вектора решения в зависимости от итерации

Результаты показывают стабильное формирование 68% верных бит при росте размерности задачи. Максимальное (минимальное) число совпадающих бит так же стабильно - 68,3% (67,7%). При этом число верно определенных бит, отвечающих именно битам сомножителей, приблизительно равно 67,9%. Примечательно то, что результат достигается всего за 500-1000 итераций, стартуя со случайно сформированного приближения.

На рис. 2 представлены результаты формирования среднего и максимального числа верно определенных бит при увеличении длины ключа. Отметим, что найденные переменные являются ключевыми для решения задачи, т.е. после подстановки их верных значений в исходную КНФ формула оказывается легко разрешимой относительно оставшихся пе-

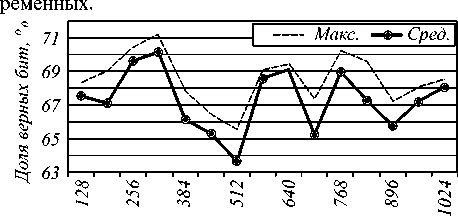
Размерность задачи факторизации, бит

Рис. 2. Процент совпадающих (верных) бит вектора приближения и вектора решения в зависимости от размерности задачи

Среднеквадратичное отклонение статистических данных не превышает 10 - 2. Это говорит о стабильном поведении метода на данном типе задач.

Таким образом, для КНФ, эквивалентных задачам факторизации больших размерностей, метод формирует различные векторы приближений, каждый из которых совпадает с решением приблизительно на 68%. В качестве развития данного результата предлагается специально разработанная система тестов, которая позволяет с высокой степенью вероятности определять биты непосредственно сомножителей.

Одним из таких тестов может служить проверка обстоятельства кластеризации ненулевых строк в матрице умножения классическим «столбиком» числа p на число q в двоичной системе счисления. Каждая строка матрицы умножения состоит либо из нулей, либо из бит числа p . Аналогично, столбец матрицы умножения будет или нулевым столбцом, или столбцом, в котором записано число q . Подставляя в данную матрицу найденные вектора приближений и сравнивая строки и столбцы получившейся матрицы соответственно с p , q или нулевым вектором, можно с определенной долей вероятности выявлять значения неизвестных. Повторяя данную процедуру с различными векторами приближений, можно строить методы голосования, повышающие вероятность определения верных значений неизвестных.

В табл. 3 представлены значения вероятностей верного определения значений бит для 31 независимого примера с помощью данного теста (при размерности чисел сомножителей 256 бит). Так, для задачи факторизации числа длиной 512 бит с вероятностью большей или равной 0,8 определяются биты 1, 13, 46, 73, 86, 101, 142, 217, 255 каждого из сомножителей.

Таблица 3. Результаты численных экспериментов по определению наиболее вероятных бит в сомножителях факторизуемого числа размерности 512 бит

Число совпадений с точным решением в 31 тесте	Частота сов-падения, %	Количество совпавших бит	Доля совпавших бит в процентах от общего числа неизвестных бит (от 512 бит сомножителей), %
31	100	2	0,4
30	96,77	1	0,2
26	83,87	1	0,2
25	80,65	1	0,2
24	77,42	2	0,4
23	74,19	8	1,6
22	70,97	9	1,8
21	67,74	21	4,1
20	64,52	50	9,8
19	61,29	66	12,9
Сумма		161	31,45

Дополнительным тестом является то обстоятельст- во, что функционал (1) после подстановки верных значений указанных бит в исходную КНФ принимает значение меньшее, чем после подстановки их неверных значений. Это позволяет практически точно определять расстановку нулей и единиц в позициях 1, 13, 46, 73, 86, 101, 217, 255. В табл. 4 приведены результаты численных экспериментов по данному тесту.

Таблица 4. Результаты численных экспериментов по определению наиболее вероятных бит в сомножителях факторизуемого числа размерности 512 бит методом сравнения значений функционала (усредненные значения для 30 тестовых КНФ)

Тестируемый бит	Значение функционала при подстановке:		Разница значений функционалов
	верного значения тестируемого бита	неверного значения тестируемого бита
13	261,2	263,7	- 2,5
46	260,8	263,5	- 2,7
73	263,0	265,0	- 2,0
86	254,5	256,7	- 2,2
101	255,0	257,3	- 2,3
142	263,2	259,8	+ 3,4
217	263,7	266,9	- 3,2

Аналогичные результаты получены и при выборках из двух и более бит. Полученные результаты ставят под сомнение криптографическую стойкость алгоритма RSA, так как распараллеливание по вариантам и выбор тех вариантов расстановки нулей и единиц в позиции 13, 46,.., при которых значение функционала минимально, позволяет практически точно определять биты сомножителей с номерами 13, 46, ....

В качестве развития данной работы предполагается дальнейшее исследование дополнительных тес- тов и построение различных методов голосования для определения конкретных битов сомножителей.