Неравенство Белла в системах с числом частиц m = 2, 3, 4

зорных произведений матриц р k ^ и р (² :

р = К Pkр^ 0 рk2),        (1)

Квантовые состояния делятся на два класса: запутанные и сепарабельные [1]. Запутанные состояния отличаются от сепарабельных, в частности, тем, что могут нарушать неравенство Белла [2]. Существует критерий сепарабельности квантовых состояний [3, 4], являющийся необходимым, но не являющийся достаточным условием сепарабельности. Проблема запутанности квантовых состояний (нахождение критерия и меры запутанности) в окончательном виде не решена до сих пор. Поэтому критерий и свойства запутанных состояний, в частности, связь запутанности с нарушением или выполнением неравенства Белла [2] для различных экспериментально реализуемых квантовых состояний, заслуживают подробного изучения. В рамках томографического подхода в работе исследуется зависимость возможного нарушения неравенства Белла от числа частиц для состояния вида I*) = 1 / V2( | 0 ) 1 1 0 ) 2 + П 1 W 2 ) .

• II.    Запутанные состояния

В квантовой механике состояния подразделяются на запутанные и сепарабельные [1, 5]. В частности, для системы из двух частиц с матрицами плотности ри рсепарабельное состояние этих двух частиц описывается матрицей плотности ρ, представимой в виде выпуклой суммы тен- с коэффициентами pk ^ 0, удовлетворяющими условию нормировки

52 pk =1 •

k

Напротив, состояния, не представимые в виде (1), носят названия запутанных. Примерами запутанных состояний являются состояние ЭПР пары: 1К) _ВРЯ = ( It) 1 0 Ю 2 - Ю1 0 It) 2 ) /^2 , [6] — и чётные и нечётные когерентные состояния (так называемый кот Шредингера): |K) sc = N ( \ae i^v ) ± |— 'a ^{- y} ) ) /V 2 . Запутанность является одним из наиболее интересных свойств, принципиально отличающих квантово-механическое состояние от классического.

В настоящей работе рассматривается связь запутанности с возможным нарушением неравенства Белла в рамках томографического подхода [7, 8].

• III.    Квантовая томография

Помимо стандартных методов описания состояния посредством матрицы плотности и волновой функции в квантовой механике вводятся функция Вигнера W ⁽ q,P ) [9]:

W (q,p) = [ К (q + U) <(q — U) e-p‘fc (2)

и симплектическая томограмма ш ( X,ц,v ) [7] (для двумодового случая):

^{ш (} X,^^,v ) =

(2 п ) ²

| W ( q,P ) 5 ( X — цq — vp ) dqdp, (3)

где ц = ( ц i ,ц ₂ ) и v = ( v i ,v ₂ ) — параметры симплектического преобразования. Функции (2) и (3) также полностью описывают систему и позволяют восстановить как матрицу плотности, так и волновую функцию. При этом симплектическая томограмма (3) является плотностью вероятности случайной действительной величины X и обладает всеми свойствами классической плотности вероятности, будучи действительной положительной величиной, нормированной на единицу.

Таким образом, вероятность того, что при измерении компоненты вектора X = ( X 1 ,X ₂ ) принимают положительные или отрицательные значения, определяется редуцированными томограммами ш ±± ( ц,v ) :

Представленная конструкция вероятностей, определяемая формулами (4) — (7), годится для описания двухчастичной системы. Увеличение числа частиц в системе приводит к увеличению размерности фазового пространства D = 4 ( m = 2 ) ^ D = 6 ( m = 3 ) ^ D = 8 ( m = 4 ), что в свою очередь увеличивает число возможных комбинаций при измерении знака компонент вектора X до 8 ( m = 3 ):

^ш +++ ⁽ Ц^,v )

∞∞

dX 1

dX ₂ х

∞

^Х I ^{ш (} X 1 ,ц 1 ^,V 1 ^,X 2 ,ц 2 ^,V 2 ^{,X 3} ,ц ^{3 ,V} 3 ) ^{dX 3} , 0

О m=3 = ( ш +++,ш ++-,ш+- +,ш-++,ш--+, ш-+-,ш+--,ш---)          (8);

и до 16 ( m = 4 ):

∞∞∞

ш ++ ( ц 1 ,v 1 ,ц 2 ,v 2 ) =

∞∞

dX 1

| ^{ш (} X 1 ,ц 1 ^,v 1 ^,X 2 ,ц 2 ^,v 2 ) ^dX 2 , 0

=    dX 1

-

∞

^ш ++++ ( Ц^,v )

dX 1   dX 2

ш -- ( ц 1 ,V 1 ,ц 2 ,V 2 ) =

| ^{ш (} X 1 ,ц 1 ^,v 1 ^,X 2 ,ц 2 ^,v 2 ) ^dX 2 , ⁽⁵⁾

-

∞

причём индекс + или — для каждой компоненты вектора X соответствует знаку бесконечности в пределах интегрирования. Аналогично, следующие выражения являются вероятностями того, что X ₁ и X ₂ разного знака:

ш + - ( ц 1 ,v 1 ,ц 2 ,V 2 ) =

го        0

= | dX 1 | ^{ш (} X 1 ,ц 1 ^,v 1 ^,X 2 ,ц 2 ^,v 2 ) dX 2 , ⁽⁶⁾

∞ ш- + ( ц 1 ,v 1 ,ц 2 ,v2) =

∞

= | dX 1 I ^{ш (} X 1 ,ц 1 ^,v 1 ,X 2 ,ц 2 ^,v 2 ) dX 2 . ⁽⁷⁾ ^    0

dX ₃ х

∞

^Х I ^{ш ( X} 1 ,ц 1 ^,V 1 ^,X 2 ,ц 2 ^,V 2 ^,X 3 ,ц 3 ^,V 3 ^{,X 4} ,ц ^{4 ,V} 4 ) ^dX 4 , 0

ш ++++ ,ш - +++ ,ш + - ++ ,ш ++ - + , ш +++ - ,ш -- ++ ,ш - + - + ,ш + -- +

.

ш + -+-,ш-++-,ш++---,ш----+, ш-+,ш+-,ш+,ш/

' m =4

Набор комбинаций для трёхчастичных (О m =3 ) и четырёхчастичных (О m =4 ) систем представлен выражениями (8) и (9) соответственно.

Однако неравенство Белла сформулировано для системы с числом частиц m = 2 , поэтому, чтобы изучать проблему запутанности в системах с большим количеством частиц, необходимо переопределить редуцированные томограммы ω ±± . В данной работе мы предлагаем определять ω _±± как суперпозицию редуцированных томограмм из наборов (8) и (9). К примеру, предлагается использовать несимметричные комбинации:

^ш ++ ⁽ Ц^,v ) = ^ш +++ + ^ш ++ - + ^ш - ++ ,

^ш + - ⁽ ц^,v )= ^ш + - +         ⁽¹⁰⁾

для трёхчастичной системы и ш ++(^,v) = ш ++++ + ш-++++ш-+-++

+ш+-++ + ш++- + + ш+++- + ш—++, ш + - (M,v )= ш-++-        (11)

для четырёхчастичной соответственно. Две другие томограммы ( ш - ₊ ,ш ) получаются при замене в (10) и (11) индекса + на —.

Представленный томографический подход и сами вероятности (4) — (11) используются при выводе параметра Белла.

• IV.    Неравенство Белла

  Эйнштейн, Подольский и Розен ещё в 1935 году обратили внимание на существование квантовых корреляций между двумя удалёнными частицами. Позже Белл из общих соображений сформулировал неравенство Белла [2], которое можно использовать для детектирования запутанных состояний. При этом нарушение неравенства Белла указывает в пользу наличия в составной системе чисто квантовых корреляций.

Существует большое количество возможных форм неравенства Белла. Такое разнообразие в основном связано с различными видами оптических экспериментов по проверке его выполнения или нарушения. В данной работе рассматривается неравенство Белла в форме CHSH (Clauser–Horne–Shimony–Holt) [10]. Для удобства далее приводится анализ только для состояния двух частиц. Определим функцию корреляции, используя (4) — (7):

E(M,v) = ш++(M,v) — ш + -(M,v)—

—ш- +(ц,р) + ш__(ц,р).

В случае системы из двух частиц со спинами 2 функция E ( ц,и ) определяет корреляцию проекций спинов этих частиц на различные направления. Таким образом, для четырёх возможных направлений: ( ц 1 ,v 1 ) , ( Ц 2 ,v ₂ ) , ( Ц 1 ,v 1 ) , ( ц 2 ,v 2 ) неравенство Белла в CHSH форме имеет вид

B = E (Ц1,V 1,Ц 2,v2 ) + E (ц 1,v 1 ,ц2,v2 ) +

+E(Ц1,v 1,ц2,v2) — E(Ц1,v 1 ,ц2,v2) I ^ 2. (12)

Заметим, что нарушение неравенства (12) с необходимостью свидетельствует о запутанности исследуемого состояния, в то время как при его выполнении нельзя сделать вывод о сепарабельности состояния.

Рассмотрим возможное нарушение неравенства Белла на примере суперпозиции квантовых осцилляторов вида |*) = 1 /V 2 ( 1 0 > 1 1 0 > 2 + |п> 1 |п> 2 ) .

• V.    Результаты

Для состояния

№ = 1 /V2 (10> 110> 2 + |п> 1 |п> 2)

функция Вигнера задается выражением e-q 2-q 2 -p 1 -p 2

W(q,p) =----2П----x

x (1 + 2r( q 1 — ip 1) n (q2 — ip2) n+ п!

+-r( q 1 + ip 1) n (q 2 + ip 2) n+ п!

+Ln (2q2 + 2p 1)Ln (2q2 + 2p2)^ , где Ln(z) = ezddn (e-zzn) — полином Ла-герра. Выполнив последовательно анализ (3) — (7), получим следующий набор редуцированных томограмм:

ш++,--(M,v) =

1 , ^НП- 1⁽⁰⁾^     , • A n/      , • A n ,

= 4 + 2n+1 пп!((Ц1 + iV 1) (Ц2 + iV2) +

+ ( Ц1 — iv 1) n ( Ц 2 — iv2) n ),

ш+-,- +(M,v) =

1    Hn-1(0)^    n . W( , .

= 4 — 2n+1 пп!((ц 1 + iV 1) (ц2 + iV2) +

+(ц 1 — iv 1)n(ц 2 — iv2) n), где Hn (x) = (—1)nex2 dn ^e-x2) — полином Эрмита. Параметр Белла для состояния \ф> = 1 /^2 (10> 1 10>2 + |п> 1 |п>2) представлен на рис. 1. Максимальное значение Bmax для соответствующих параметров не превосходит 2. Таким образом, в рамках выполненного анализа для указанного состояния нарушение неравенства Белла не зарегистрировано.

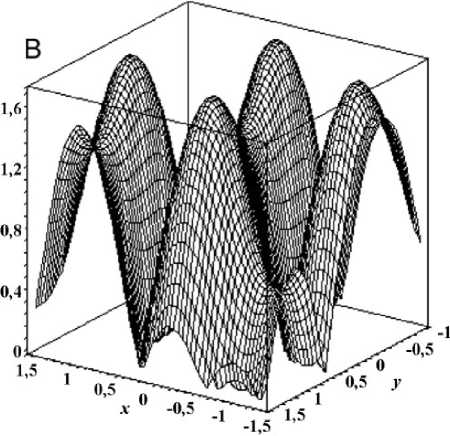
Рис. 1. Параметр Белла B ( x,y ) для двухчастичной суперпозиции М = 1 /^ 2 ⁽ 1 0 ⁾ 1 | О ⁾ 2 + |п) 1 n 2 ) ⁽ Ц 1 = COS⁽ x ), v 1 = sin( x ), ц ₂ = cos(2 x ), v ₂ = sin(2 x ), Ц 1 = cos( y ), v 1 = sin( y ), Ц 2 = cos(2 y ), v 2 = sin(2 y ), n = 1)

Для случая трёхчастичной и четырёхчастичной систем ( m = 3 и m = 4 ) с волновыми функциями

| Ф ) m =3 =

-/=( In) 110 ) 2|0 ) з+

+10) 1 In)210)3 + 10) 110)2 |n)3)

и

| Ф )т=4 = 2(10 ) 1 |n) 2 |n) з |n) 4+

+ n) 1|0) 2 |n)3 |n)4 + |n) 1 |n) 2 |0)3 |n)4 +

+ |n) 1 |n) 2 |n) 3|0 ) 4)

и набором несимметричных комбинаций (10) и (11) параметр Белла представлен на рис. 2а ( m = 3 ) и рис. 2б ( m = 4 ) соответственно. Обнаружено нарушение неравенства Белла с максимальным значением B max - 2 , 26 ( m = 3 ) и B max - 2 , 06 ( m = 4 ).

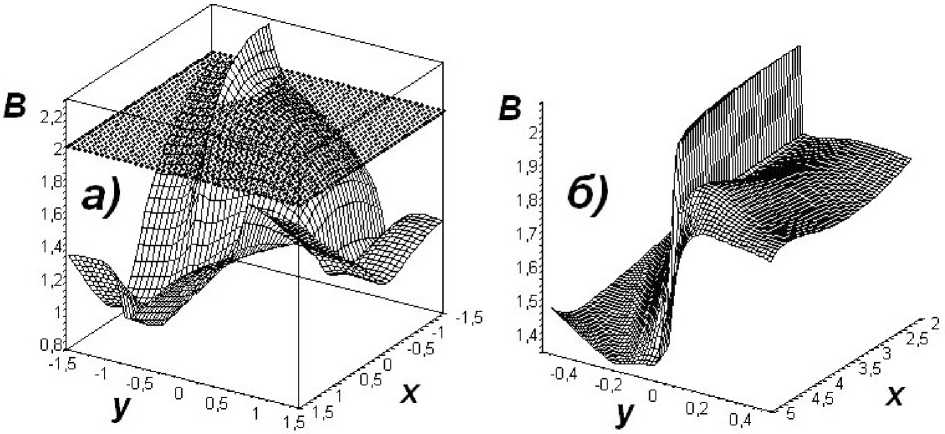
Рис. 2. Параметр Белла B ( x,y ) для систем (а) | Ф ) _т =3 ( ц 1 = cos( x ), v 1 = sin( x ), ц ₂ = exp(2 y ), v 2 = exp( -y/ 5), ц 3 = exp(3 x ), v 3 = exp( -x/ 3), Ц 1 = exp(5 x ), v 1 = 0 , 2, Ц 2 = cos(2 y ), v 2 = sin( y/ 5),); (б) | Ф ) m =4 ( Ц 1 = cos( x ), v 1 = sin( xy ), ц 2 = exp( x ² ), v 2 = sin(2 y ), ц 3 = In |xy| , v 3 = x y , ц 4 = x ² , v 4 = y ² , Ц 1 = sin(exp( y ² )), v 1 = exp( x ² y ² ), Ц 2 = 1 /x + 1 /y , v 2 = sinh( x ), n = 1)

• VI.    Заключение

Подводя итог выполненного анализа, укажем, что для двухчастичного состояния нарушение неравенства Белла не зарегистрировано. Напротив, для состояний | Ф )m=3 и | Ф )m=4 в рамках представленного способа определения редуцированных томограмм (10), (11) зафиксиро- вано нарушение неравенства Белла. При этом найденное максимальное нарушение Bmax — 2,26 не превышает критерий Ци-рельсона 2V2 [11].