Несоразмерная магнитная структура в антиферромагнетике с сильным обменным взаимодействием между делокализованными и локализованными электронами

Образование несоразмерных структур часто наблюдалось в низкоразмерных системах со спином, как в RbCuCl 3 [1], и индуцированной полем решетке магнитных солитонов в спин-пайерлсовских соединениях CuGeO 3 [2]. Причиной формирования несоизмеримости является конкуренция различных взаимодействий: антиферромагнитные обмены между ближними и ближайшими соседями [3], взаимодействия Дзялошинского – Мориа и взаимодействие между магнитными системами и упругими [4] или электронными системами [5] с несоразмерным периодом структуры. Несоразмерная структура в трехмерной упорядоченной магнитной решетке обнаружена в CuB 2 O 4 [6]. При понижении температуры ниже происходит второй магнитный фазовый переход в сторону несоразмерного трехмерного магнитного порядка. В несоразмерной фазе, но вблизи, на нейтронограмме появляются сателлиты более высокого порядка. CuB 2 O 4 кристаллизуется в пространственной группе с постоянными решетки a = 11,528 Å и c = 5,607 Å [7]. Существование такой магнитной структуры было объяснено релятивистскими эффектами, такими как спин-орбитальное взаимодействие, которое приписывают своего рода взаимодействию Дзялошинского – Мориа (ДМ). Используя ДМ взаимодействие и анизотропию в базисной плоскости, модуляция параметра порядка в метаборате меди вдоль направления спирали описывается в рамках теории фазовых переходов Ландау решением уравнения синус – Гордона. Магнитная структура меняется в результате взаимодействия с упругой подсистемой [8; 9]. Взаимодействие спинов с оптическими [10] и акустическими [11] модами колебаний приводит к уменьшению намагниченности и при некоторых критических параметрах к исчезновению дальнего магнитного порядка [12; 13]. Возможно также увеличение поля магнитной анизотропии в результате четырехспинового обмена [14; 15].

В данной работе рассматривается взаимодействие двух подсистем: магнитной и электронной. В зависимости от величины взаимодействия между носителями тока и локализованными спинами необходимо рассматривать новые квазичастицы – спиновые поляроны. В этом случае возможно образование несоразмерной магнитной структуры. В данной работе предлагается микроскопическая теория образования несоразмерной магнитной структуры в CuB 2 O 4 .

Модель

CuB 2 O 4 проявляет слабые пьезоэлектрические свойства [16]. Таким образом, одноосное давление вдоль [011] вызывает электрическую индукцию. Скорость акустических поперечных волн, распространяющихся вдоль [100] анизотропна для поляризации волн, [010] и [001] [16]. Эти результаты свидетельствуют о существовании анизотропии распределения электронной плотности в пределах ~ 8 %.

Можно предположить, что электрические свойства метабората меди обусловлены связанными состояниями электронов и дырок. Разность энергий ионизации ионов меди и бора Cu2+,

B 3+ составляет а( E B 3 +

E C 2 + ) ~ 1 эВ [17], и они связаны ковалентной связью через кислород.

Смещение электронной плотности на ковалентной связи может увеличивать эффективный заряд меди и уменьшать заряд бора. Это можно интерпретировать как образование дырки в ионе меди. Сильное взаимодействие дырок с возбуждениями антиферромагнитно упорядоченной спиновой подсистемы описывается в рамках s–d-модели. В этом случае хорошей квазичастицей является более сложное возбуждение – спиновый полярон.

Определим низколежащие спин-поляронные состояния, используя приближение среднего поля в модели решетки Кондо [18]. Гамильтониан имеет вид:

H = H 0 + H 1 + H 2 ,

^H о = E ( t h p a r+ h p ,. a r ,. ⁺ t h c a Lh c ,. a r ,. ⁺ e. c . ) = E ^e k a ⁺ ,. a k ,. ,                     ⁽¹⁾

r , g                                                             k

H1 = J E aJ,..5r“.^ar,.2, r,ai,a2

H 2 = 2 1 E 5 r+g 5 a .

r , g

Здесь узлы r образуют тетрагональную решетку; h _p и h_c – расстояния до ближайших соседей в плоскости и вдоль оси c ; a k . - оператор рождения дырок со спиновыми индексами . = ± 1; H ₀ описывает перескок носителей заряда; t _h p = - t 1 ; t h c = - t 0 ; H 2 - антиферромагнитное взаимодействие локализованных спинов 5 = 1/2 с их ближайшими соседями; H 1 - гамильтониан локального взаимодействия Кондо; .^a - матрицы Паули и a = x , y , z .

Запишем первые два уравнения для функций Грина, описывающих движение дырки на антиферромагнитном фоне. Используя приближение случайных фаз, составлена система уравнений для функций Грина ^ a _{r > a}| a J, _a^ и ^ b _r , .| a^^ ^, b r . = 5 _r “ . .. 1 a _r . 1 , a = x , y замкнуто. Эти уравнения имеют следующий вид:

(M ek) Gk =1 + у Gk2,

(го- ek) Gk = J (1 + m - 2 nm) Gk,

ek

G k ¹

-

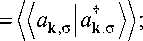
Ц ,

G k ²

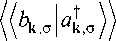
Jm

= e0 *

k 4

e k = - 2 1 1 ( cos k_x + cos k y ) - 2 1 ₀ cos k z ,

. о . / m . Y z T ek = 2 zce. + J — + n +—ml - u, k k (2 J 2

n = ( a | a ^ + a | a ^ V

Здесь b _k . , a _k . и G _k - преобразования Фурье соответствующих локальных операторов и функции Грина соответственно; c = ^ 5 _r ^x 5 _r ^x _+g + 5 _r y 5 _r y _+g^ - спин-спиновая корреляционная функция на поперечных компонентах спина; z – число ближайших соседей; m – намагниченность подрешетки. Все энергии отсчитываются от химического потенциала ц .

Решение системы уравнений (2) приводит к следующему спектру возбуждений:

^го 1,2 ^{( k} ) = 2

ek

+ek ±J(ek

x 2 _r2f 1 + m

- e _k ) + J I-- nm

Химический потенциал рассчитывается из самосогласованного решения уравнения для концентрация дырок n

n=^f £/d ю f (°) П Im Gk,

где f ( rn ) = ( exp ( to / T ) + 1 ) . Суммирование по импульсу в зоне Бриллюэна производится с использованием 8 × 10⁶ точек.

-4

0.0     0.5     1.0

c

T=12, K к / п

0.5     1.0

0.5     1.0

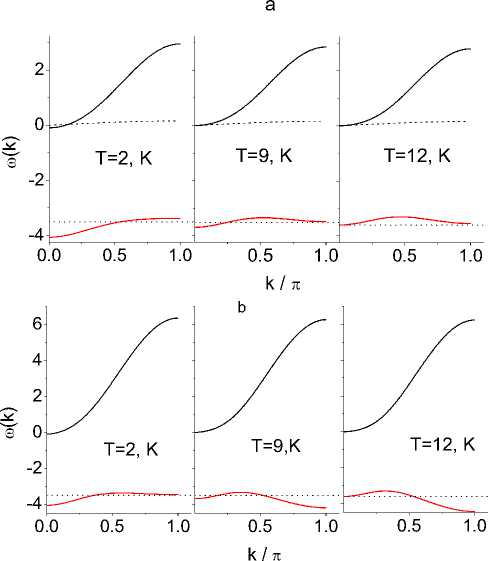
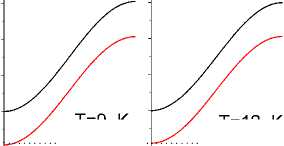
Рис. 1. Дисперсионные ветви спин-поляронных возбуждений вдоль [001] ( а ); [101] ( b ); [111] ( c ) при разных температурах. Горизонтальная линия указывает положение химического потенциала в нижней полосе (пунктирная линия)

Fig. 1. Dispersion branches of spin-polaron excitations along [001] ( a );

• [101]    ( b ); [111] ( c ) at different temperatures. The horizontal line indicates the position of the chemical potential in the lower bar (dashed line)

Для вычисления подрешеточной намагниченности и спин-спиновой корреляционной функции запишем четыре дополнительных линейных дифференциальных уравнения для функций

Грина <(Sг“у ^га/V \vГ^у S“у'ii Для Двух подрешеток Y,Y' = 1,2 и два уравнения для намагни- ченности подрешетки и корреляционной функции. Задачу можно упростить, если мы рассмотрим магнитную систему в адиабатическом приближении и сделаем некоторые оценки темпера- турной зависимости m, c. Процедура разложения по свободной энергии дает степенную функцию m = m0л/1 - T/TN . Согласно данным упругого рассеяния нейтронов [6] намагниченность подрешетки составляет m0 = 0,94цB при T = 2 K . Функция спин-спиновой корреляции для ближайших соседних узлов может быть оценена при температуре Нееля как

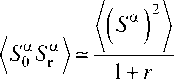
5 (1 + 5

V ■ /еаса \-П1?5 х ; \⁵ 0 ⁵ r =1 / = 0, ¹² 5.

3(1 + Г)    '         '

При низких температурах, когда радиус корреляции спиновых флуктуаций ^ ~ a (а - постоянная решетки), поперечная спин-спиновая корреляционная функция вычисляется в приближении среднего поля (5015^=1) = 0,125 (1 - m2). Зависимость c (T) в парамагнитной фазе считается симметричной относительно температуры Нееля.

Для тетрагональной симметрии а (постоянная решетки в плоскости) >  c параметры перескока носителей тока также следует рассматривать как анизотропные t1 /t ₀ = 0,92 .

Обсуждение результатов

Спектры возбуждения поляронов для трех направлений показаны на рис. 1 для следующих параметров: I/t ₀ = 0,08, Jt ₀ = 2,06. Зонное расщепление свободных электронов наблюдается вследствие сильного взаимодействия с локализованными спинами, образующими упорядоченное состояние ниже температуры Нееля. Уровень Ферми расположен в нижней зоне около химического потенциала, обозначенного на рис. 1 пунктирной линией. Энергия Ферми и s–d энергия взаимодействия имеют сопоставимые значения. S-электроны образуют волну спиновой плотности (ВСП) с волновым вектором, расположенным вблизи поверхности Ферми, поскольку энергия Ферми более чем на порядок превышает энергию магнитного возбуждения. ВСП модулирует плотность локализованных спинов, что вызывает появление дополнительных сателлитов на нейтронограмме.

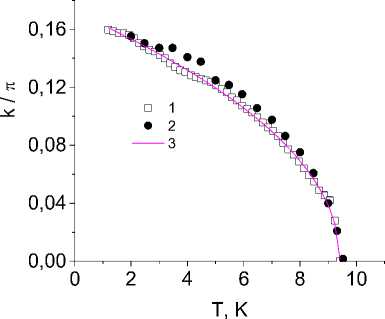
Рис. 2. Температурная зависимость импульса Ферми ( 2 ) и положения сателлита на нейтронограмме ( 1 ). Кривая представляет собой аппроксимирующую 0,48 функцию Q ( T ) ~ ( T - T )    ( 3 )

Fig. 2. Temperature dependence of the Fermi impulse ( 2 ) and the position of the satellite in the neutron diffraction pattern ( 1 ). The curve is an approximating

0,48

function Q ( T ) ~ ( T - T )     ( 3 )

0    5    10   15   20   25

T, K

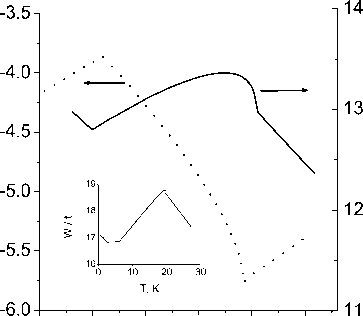
Рис. 3. Энергия нижней границы полосы W_bot t и верхней границы полосы W_top t в зависимости от температуры. На вставке показана температурная зависимость ширины полосы

Fig. 3. Energy of the lower border of the band and the upper border of the band as a function of temperature. The inset shows the temperature dependence of the bandwidth

Установлено, что эволюция положения сателлитной линии с температурой происходит по степенному закону [6]

Q ( T ) да ( T * - T ) ^V ,                                         (6)

с v = 0,48, как показано на рис. 2. Расчетное изменение импульса Ферми k F вдоль [001] (рис. 2) в зависимости от температуры хорошо согласуется с экспериментальными данными. Расчетное значение k F = ( 0,0,0.14 ) при T = 1,8 K также согласуется с периодом спиновой модуляции Q = ( 0,0,0.15 ) . Поверхность Ферми представляет собой ограниченную область с центром зоны при T <  T* и обращается в нуль при T = T* . Импульс Ферми лежит в диапазоне п/2 <  k F <п с центрами на краях зон, где спин-волновой спектр в CuB 2 O 4 не наблюдается. Уменьшение эффективной энергии взаимодействия s-электронов с локализованными спинами, вызванное уменьшением намагниченности подрешетки, приводит к сдвигу дна и вершины поляронной зоны и увеличению ширины полосы, как показано на рис. 3. В парамагнитной фазе рост антиферромагнитных корреляций при охлаждении также приводит к увеличению полосы пропускания.

Для оценки вклада поляронных возбуждений в теплоемкость среднее значение кинетической энергии полярона K_p моделируется функцией Грина

K p = 77 £ ^ю( ^k ) ¹J dEf ( E ) Im G" 2 ( E ) •                       (7)

N k ^п

Температурная зависимость C = dK_p JdT представлена на рис. 4. Максимумы теплоемкости наблюдаются при T - 1,7; 4,5 K . Температуры, соответствующие максимумам теплоемкости, хорошо согласуются с экспериментальными данными [19]. Транспортные свойства, как проводимость, могут быть получены из формул Кубо в пределе d ^ да [20]

, \ v                      \ f (го')— f (го'+го)

о ( го ) = о ₀ Е J d го ' I _о ( го ', го ' + го ) —-—------------ -, о '                                  ^го

I о (^го 1 , ^го 2 ) = -1 2 Е Im ^G о ( k , ^го 1 ) Im G о ( k , ^го 2 ) ,

n k где о0 - постоянная, определяющая размерность проводимости. Температурная зависимость проводимости о(го^ 0) представлена на рис. 5. Ниже TN величина о резко уменьшается с увеличением намагниченности подрешетки. При T∼ 16K изменение знака производной химического потенциала с dц/dT < 0 на dц/dT > 0 коррелирует с особенностью в dо/dT. Падение проводимости при T > 5 K возникает из-за смещения минимума дна зоны от центра зоны (0, 0, 0) к (1, 0, 1), (0, 1, 1). Это показано на рис. 1, b. Оптическая проводимость представлена на рис. 6 и имеет два максимума. Первый пик является результатом внутризонных переходов, а широкий максимум о(го) приписывается переходам между нижней и верхней зонами. Температурную зависимость о(T) можно наблюдать в ИК-диапазоне с амплитудой электрического поля E0 и плоской поляризованной волны с частотой го. Мощность поглощения, подаваемая в систему, определяется как P (го) = 2E0 Re [оz (го)] [21].

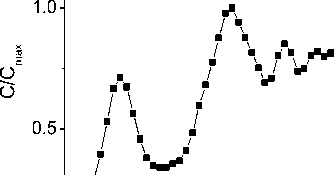
0.0

T, K

Рис. 4. Температурная зависимость теплоемкости, нормированной на максимальное значение, индуцированное спиновыми поляронами

Fig. 4. Temperature dependence of the specific heat normalized to the maximum value induced by spin polarons

0.8

0.6

0.4

0.2

0    5    10   15   20   25

T , K

0.0

Рис. 5. Температурная зависимость проводимости о ( T ) при ш^ 0

Fig. 5. Temperature dependence of conductivity о ( T ) at го ^ 0

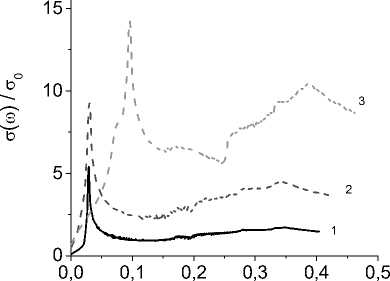
ω , eV

Рис. 6. Оптическая проводимость при температурах

T = 2 К ( 1 ), 7 К ( 2 ) и 17 К ( 3 )

• Fig. 6. Optical conductivity at temperatures

T = 2 K ( 1 ), 7 K ( 2 ) and 17 K ( 3 )

Особенности низкотемпературного поведения теплоемкости и проводимости возникают из-за модификации полосы возбуждения поляронов. Максимум плотности состояний находится вблизи уровня Ферми и смещается в область высоких энергий при T > 10 K . Увеличение концентрации дырок приводит к уменьшению критической температуры для формирования модуляции спиновой структуры T ^* . Максимум теплоемкости также смещается в область низких температур.

Заключение

Подведем основные итоги. Спин-поляризованные s-электроны образуют волну спиновой плотности с периодом, равным импульсу Ферми. Волна спиновой плотности модулирует плотность локализованных спинов в результате сильной s–d-связи. Оценка температурной зависимости ферми-импульса спинового полярона хорошо согласуется с эволюцией положения сателлита в зависимости от температуры в CuB 2 O 4 . Максимум низкотемпературной теплоемкости возникает в результате смещения минимума нижней границы зоны от центра зоны (0, 0, 0) к (1, 0, 1), (0, 1, 1). Представленные расчеты предсказывают резкое уменьшение проводимости и интенсивности инфракрасного поглощения при температуре Нееля.