Нестационарная физико-математическая модель процессов в сильноточных плазменных системах

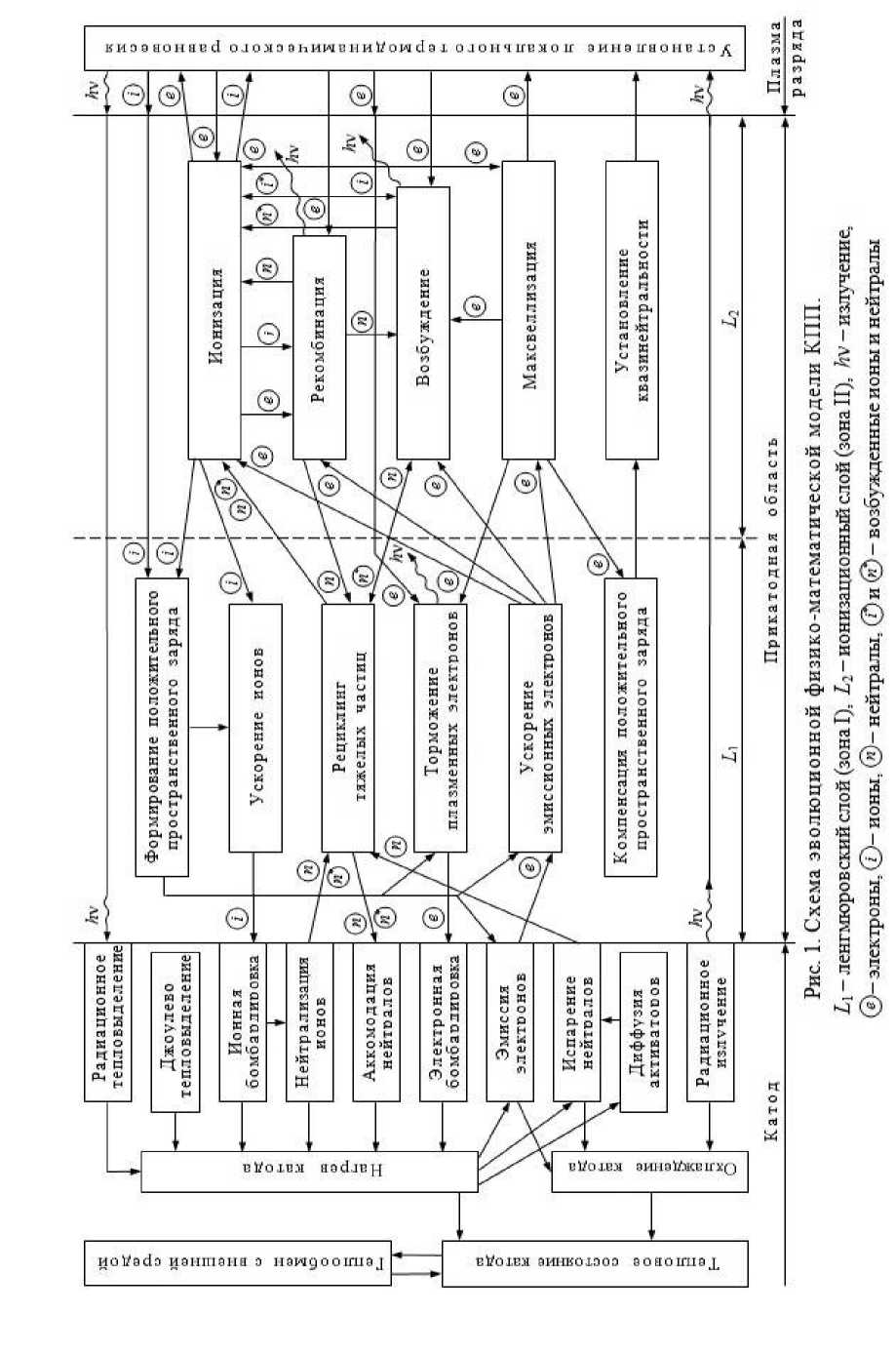
Представлена эволюционная физико-математическая модель катодных и прикатодных процессов (КПП), учитывающая динамику эмиссионных свойств электродов в процессе функционирования сильноточных плазменных систем. Схема развитой модели КПП показана на рис. 1. Она основана на решении задачи тепломассопереноса и испарения легирующих элементов тугоплавких катодов совместно с уравнениями, описывающими процессы в пространственной системе «катод – прикатодная область – дуговой канал». Замкнутая постановка обобщенной задачи позволяет исследовать закономерности и динамику во времени всей цепочки КПП в совокупности с учетом влияния плазмы столба разряда. В модели впервые рассматриваются процессы тепломассопереноса, рециклинг нейтралов и ионов в приэлектродной области и элементарные процессы, сопровождающие данный механизм. Ввиду многообразия и сложности КПП для описания их разбиваем на четыре взаимосвязанные группы, выделяя в каждой из них только основные процессы.

• 1.    Процессы в объеме твердого тела. Протекание тока, нагрев массива электрода объемными (джоулево тепловыделение) и поверхностными (тепловой и лучистый потоки из плазмы) источниками тепла. Охлаждение катода за счет испарения нейтралов и термоэмиссии электронов, кондуктивно-го и конвективного теплообмена и радиационного излучения. В активированных катодах процессы тепломассообмена зависят от диффузии и испарения атомов легирующего металла и при высоких температурных полях сопровождаются рекристаллизацией структуры матрицы.

• 2.    Процессы на поверхности катода. Испарение нейтралов, эмиссия электронов и нейтрализация ионов. Лучистый и конвективный переносы тепла. Бомбардировка поверхности твердого тела потоками возбужденных атомов, высокоэнергетичных ионов и «обратных» (плазменных) электронов, аккомодация их на поверхности. Энергообмен этих процессов.

• 3.    Процессы в прикатодной области. Образование избыточного пространственного заряда и скачка потенциала перед катодом. Ускорение ионов и электронов эмиссии в зоне положительного пространственного заряда. Торможение «обратных» электронов. Рециклинг атомов и ионов, их возбуждение и ионизация, рекомбинация заряженных частиц. Формирование потоков ионов и «обратных» электронов, установление квазинейтральности и локального термодинамического равновесия (ЛТР) на границе с ядром разряда.

• 4.    Процессы в канале разряда . Стабилизированный канал разряда состоит из областей прикатод-ной контракции и положительного столба (рис. 2, зоны III, IV) с процессами энергетического баланса: кондуктивный, конвективный и радиационный теплообмены, протекание тока и джоулево тепловыделение в объеме плазмы в приближении ЛТР.

Уравнения, описывающие процессы в твердом теле (перенос тепла, протекание тока, диффузия активатора) с соответствующими граничными условиями рассмотрены в [1–3].

Уравнения для процессов на поверхности катода, контактирующей с плазмой разряда, представ- лены в виде:

q0 + jT (фэф + 2kTIe) = jc(1 - s)(Vc + V -фэф + 2kTIe) -

-e _{1 CT} T ⁴ + q л + 0,25 a e en e <  v e >  (2 kT I e + ф эф )exp( - eV c I kT )

1T = AT2 expteфэф 1 kT), eфэф = eфw - e(eE)'

Ie = SI = J (jT - j"e°6P )dF naVa = niVi(4)

Процессы в прикатодной области (рис. 2, II) в одномерном приближении описываются следующей системой уравнений:

mknkvk (dvk 1 dx) = eknkE - grad Pk -Z mkinkvki(vk - viX (k, l = e, i, a)

l * k dФ iI dx = -pnena + an3e(6)

dФ iI dx = — dФе1 dx = dФ a I dx , Ф i = ni V i , Фе = ne V e, Ф a = П^ V a(7)

ni V i + ne V e = jOe = const(8)

p = nakTa + nekTe + nikTi(9)

jTVc = jy, + jy (Vc + 2kTe/e) + 3,2jc kTe/e je>6p = 0,25 aeene < Ve > exp(-eVc IkTe )

В (1–11) обозначения общепринятые, уравнения в различных модификациях используются в работах Ли, Гринвуда, Неймана, Зимина, Хвесюка, Мойжеса, Немчинского и др.

В настоящей работе система дополняется уравнением, связывающим эффективную работу выхода электронов со степенью покрытия 0 и распределением концентрации активатора на поверхности электрода:

e ф эф (t ) = kT(t )ln { 0 ( t )exp [ - e ф _a/k'T(t ) ] +^[ 1 - 0 ( t ) ^] exp [ - e ф м ^tT(t ) ^] }             ⁽¹²⁾

где е ф _м, е ф _а - соответственно работы выхода электронов матрицы и активатора.

Следует особо подчеркнуть, что e ф _э ф (t) является основным параметром, управляющим динамикой всей замкнутой системы эволюционной модели КПП.