Нестационарная задача теплопроводности при лазерно-плазменном нагреве

Самарский государственный аэрокосмический университет

Приводится решение задачи нестационарной теплопроводности с подвижной границей для определения температурных полей в многофазных материалах. Полученное решение позволяет рассчитать температуры в системах при совместном действии лазерного и плазменного или ионно-плазменного источников нагрева, а также найти закон движения фронта кристаллизации или конденсации при напылении.

В настоящее время все большее внимание уделяется решению задач нестационарной теплопроводности с учетом подвижной границы. Особенно острая необходимость в решении таких задач ощущается при определении температурных полей в многофазных материалах с учетом движения фронта кристаллизации или конденсации при совместном действии лазерного и плазменного или ионно-плазменного источника нагрева.

Анализ литературных данных показывает, что в аналитическом виде решен достаточно широкий класс параболических уравнений с подвижной границей для однородного материала [1-3].

В случае же двухслойного материала известны решения для двух состыкованных по-лубесконечных тел с постоянной скоростью движения границы раздела, либо при наращивании материала на полубесконечное тело с законом движения границы, имеющим специальный вид [1, 4-6].

В настоящей работе приводится решение нестационарной задачи теплопроводности для двух состыкованных тел с различными теплофизическими постоянными и с произвольным законом движения границы как заданным, так и получаемым из условий сопряжения. Граничные условия на внешних поверхностях тел могут быть первого, второго или третьего рода, на поверхности раздела материалов четвертого рода.

Задача формулируется следующим образом. Пластинка толщиной h, имеющая началь ную температуру То и коэффициенты температуропроводности и теплопроводности соответственно 21 и 11, нагревается лазерным источником и одновременно на неё наносится другой материал с теплофизическими параметрами 22 и 12.

Математическую модель сформулированной задачи можно записать в безразмерных переменных следующим образом:

— ^ ^ l = _^{д 9} 2_ Т _G [0 Z ] (1) к д £² d Fo ^С [ ^{, Z} ]’

Э29 _ Э01„ dF = dFo ’ С ' [-1’0]’ д9 2

С = л < ’

9 1 (0, Fo ) = 9 ₂ (0, Fo ) при Т = 0,

6>1«,0) = 0,(4)

I ⁹ = f 1 ( 9 1 , Fo ) при Т = -1, ∂ ξ

^= = f2(92,Fo) приТ = Т (Fo),

"; = ef (9,, Fo),(7)

∂Fo at a λ z

Fo = -зг, кп = —L, к. = —, с = -, aλ h a 2        Х2       h

Z = ^Fo), 92(Z,Fo) = 9,(Fo), h z - ось ординат, перпендикулярная поверхности подложки.

Относительные температуры подложки 0 1 и покрытия 0 2 связаны с их абсолютными значениями соотношением 0 . = Т/Т_о - 1, где i= 1,2.

Функции f, f 1 и f ₂ будут конкретизированы в дальнейшем при рассмотрении частных случаев полученного решения.

Скорость движения фазовой границы для большинства видов напыления и рационального лазерного нагрева не превышает 10-5 м/с, поэтому кинетический параметр в в уравнении (7) много меньше единицы.

Обозначим q ( Fo ) = ^- , тогда ре- ^{э /} _{ =0

шение уравнения (2) при условии (4) и (5) запишется в виде [4]

Fo

K1(0, Fo) + J q( X)K(0, Fo — X)dX = es + oo 1 2n *\n—1 у ka d___ ^71 2n! dFon—1

Z 2 n

d e s 1 dFo J

^TO    k^{2 n}      d ⁿ L ₂ n + 1 d e s 1

Z0(2n +1)! dFoⁿ p    d / J '

В соответствии с (7) обозначим Z 1 = ^в, тогда из (11) и (12) видно, что решение полученной системы можно представить в виде рядов по в<1.

Поэтому qs =1L q(2n)ь2n + q(2n+1)ь2n+1}, (n) n=0

des _ у Jde(2n) d/ "б1 d/ de(2 n+1) -

Q2n+1 I в J. (14)

0 i ( ^ , Fo ) = K i ( ^ , Fo) +

Fo                                (8)

+ J q ( X)K ( / , Fo - xW.

В случае f 1 (0_pFo) = 0 будем иметь

K ( / , Fo ) = 1 +

+ 2 ^ ( - 1) ^k exp{ — ( k ^ )² Fo } cos[ k ^ ( / + 1)], (9)

K , ( 5 , Fo ) = 0 '

Подставив Z = Z 1 P , (13), (14) в (11) и (12), проведя необходимые преобразования и сравнивая члены с одинаковыми степенями в, получим:

1 ^fF00⁽⁰⁾

е(0) = K1 (0, F0) + — J     K (0, F0 — X )dX, kл о d/

е (1) - с d e^{(0) е} = ^Z1 -/т

+ _±f r^ k л Я Э /

k a ² Z 1

d e ⁽⁰⁾ 1

d X _

х

Решение уравнения (1) можно представить в виде дифференциальных рядов [1, 2]:

х K (0, F 0 — X ) dX ,                       ⁽¹⁵⁾

то т 2n "\n —1 Г

6₂ ( / ,Fo) = F + У ~      1 1 / — Z ]²

^{2               s} П = 1 2п! d Fo n ^{- 1} [

de_s 1

—- 1 + d Fo J

_e (2 n )

(2 n )

F ₂

1 F0 de(2n) ■ kл 00 d/

+ F 1 ^{(2 n )} х

TO

+ :

n = 0

7 2n ka

d n

(2n + 1)! d Fo n

« [ / — Z ]^{2 n + 1} e ., I d / J

где 30 2 /9^1 _/ = _Z= d()dc.

х K (0, F 0 — X )d X                    (16)

1 F0 e <2«+i) = — f (2n +1) + 1 i"	"d e (2 n + 1) + F (2 n + 1) "	х
2         k J k Л 0	^ d /       1 J
х K (0, F 0 — X ) d X ,		(17)

Используя (3) и (7), получаем систему интегро-дифференциальных уравнений:

где

TO k л q(Fo)   У n=1

k ²ⁿ d ⁿ

+ > —--

П =0 2n! dFoⁿ

k^    d ⁿ

(2 п — 1)! d Fo

Z 2 п

de , 1 ------->. dFo ’

п — 1

2n—1 de s dFo

1 +

F ^{(2 n )}

n

= :

k = 1

1 2k ka

d k ^{— 1}

( 2k — 1 ) ! dF ₀ ^{k — 1}

х

.2И de(2"—2k+1)    1 d х — L2k 1 х---------+--

¹        dF ₀       2k dF ₀

Z 1 ^{2 k}

d e <2«—2k)

d /

F 1(2 n + 1)

^k ^2k д k

= > —-- x^X £ 2k! дР^

х Z .

дд (^2л -^k ⁺¹¹ х

д^

^K a    Г 2 k + 1

2 k + 1 ¹

дд < ² ” - 2 k )

дР„

,

ным вакуумным напылением.

Разложим (18) в ряд по в и подставим в (15) - (17). Решим полученное интегральное уравнение (15) преобразованием Лапласа. С учетом условий (9) получим:

n

FT) = l k=1

k 2( k - 1)

д^{k - 1}

(2k - 1)! дЕ ^ ^{- 1}

х

д ⁽⁰⁾ =

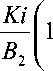
м

-lD( Л n )exP{- Л 2 F0} n=1

х

2             (2 n - 2 k )

kr z ^{2 k дд}Z ^{2 k} -¹

2k        дР ₀     ¹¹

дд (2n-2k+1) "  X---—--- .

х sin 2 л где П(цп) =           n----, Лn - корень

0,5sin2 л _п + Л n

д^

,

уравнения ctg л _n

F (2n + 1) = у k 21 ^д k ¹

^{2       1} 2k! дР^{к - 1}

у k^2k д ^k b(2k +1)! др

2 k

2 k+ 1

дд (2n - 2 k +1) др дд ^{(2 n - 2 k}) 1

х д^

•

Полученная система рекуррентных соотношений (15)-(17) позволяет найти решение поставленной задачи в случаях, когда уравнения движения границы задано явно в виде функции f ( д s , F ₀ ) = f ( F ₀ ) при различных граничных условиях. Так, в случае граничных условий второго рода на фазовой границе необходимо вычислить 0 (0-) из (15) и подставить в (16), что даст 0 ⁽¹⁾ Полученные 0 (0-) и 0 (1 ^подставляем в (17). Проводя последовательно такие подстановки, находим 0⁽ n и тем самым 0s - температуру фазовой границы. Используя (11), (10) и (8), находим искомое распределение температур.

В случае граничных условий первого и третьего рода необходимо на каждом этапе нахождения соответственно д0^(п)/д^ или 0⁽ⁿ⁾ применять к соотношениям (15) - (17) либо преобразования Лапласа, либо метод последовательных приближений.

В качестве примера рассмотрим вычисление 0s в следующем, часто встречаемом в практике, случае:

ддs-Ki Ki дZ

Ki + Ki д^           ¹ др 0

-

Вд s , Z = №, (18)

где Ki, Ki 1 и B₂ - постоянные.

Сформулированное граничное условие (18) может быть выведено и проанализировано в дальнейшем при рассмотрении нагрева лазерным источником и ионно-плазмен

= л А

B 2

Подставим (19) в (16) и решим полученное интегральное уравнение также преобразованием Лапласа:

д(1)

м

= I ¹ - l^{D (} Л п ^)еХР ^{- Л„^Р 0 ^{} -} А

^B ₂ I      n =1                          ) ²

d 1 d

l n=1 Лп L dЛ Л dЛ

( Л А Л ⁾⁾²exp ^{- Л ² F 0 ^}

k2 v 1 х — l — kx -1 Лп dЛЛ dЛ

d 1 d

л = л „ ^{Ki х}

⁽ Л О₁( Л ⁾⁾²exp ^{- л ^{2 F} o ^}

л = л n ’

.       cos2Л где D1(Л) = o .

0,5sin2 Л + Л

В (20) при обратном преобразовании Лапласа была использована теорема разложения для случая трехкратных корней [4]. Аналогично находится 0^(п), что и решает постановленную задачу.

Как показывает анализ, факториальный вид рядов в (10), (15) - (17), условия в<1,

д д _s

Z(F)<1 и ограниченность Z х— при F ^0 о                              дР₀          о

обеспечивает их быструю сходимость.

Рассмотрим распределение температур и формирование покрытия при нагреве лазерным источником и ионно-плазменном вакуумном напылении [10]. Получим в явном виде значения функций /, / 1 , /₂ и параметра р.

При ионно-плазменном вакуумном напылении плазма, состоящая из ионов материала катода, генерируется в катодных мик-

ропятнах, доускоряется, доионизируется в торцевом холловском ускорителе и направляется на основу. При подаче на основу отрицательного потенциала ионы получают также дополнительное ускорение в дебаевском слое. Сталкивающиеся с поверхностью ионы могут отражаться от поверхности, распылять ее, конденсироваться на ней, а также вступать в химические реакции при подаче в камеру легирующего газа. В области энергии ионов, характерных для режимов получения покрытий (до 200эВ), процессы отражения и распыления незначительны [3]. Наблюдаемый при этом разогрев основы происходит из-за выделившейся кинетической и потенциальной энергии метастабильных атомов, образовавшихся в результате выделения энергии кристаллизации и энергии образования химического соединения.

Процесс напыления обычно проводится в вакууме при давлении не выше 133-10-3 Па, поэтому основной причиной охлаждения системы при больших температурах является теплоизлучение. Отвод тепла через места закрепления подложки во время процесса напыления незначителен, так как подложко-держатель нагревается тем же ионным потоком и перепад температур АТ между ними мал.

Тепло же, переданное между такими системами в вакууме, дается соотношением

где

Ki ^— yhy { /’ (Ey ^{+ U}c^{Ze -} Ze^ ) + q „ ^} ^ 2 ^Т 0

- ech

„⁴ __T4

0 c_CT .

Ki 1

AHp ₂ a ² у _— 4echT 0

Z ₂ T ₀ Nm ’ ^{2 —} X ₂

q _ё - плотность потока лазерного излучения, j - плотность потока ионов, Е₀ - средняя кинетическая энергия ионов, Ze - средняя кратность ионизации потока, Uc - потенциал ос

новы, ei - средняя энергия ионизации потока, ф - работа выхода с поверхности конденсации, £ - приведенный коэффициент излучения покрытия, о - постоянная Стефана -Больцмана, Т_СТ - температура стенок камеры, АН - тепловой эффект кристаллизации и образования соединения, N - число Авогадро, т - масса молекулы соединения.

В (21), исходя из возможностей аналитического представления решения, а также учитывая, что при напылении стараются ограничивать перегрев, выражение T ₀ ⁴ (1 + 0 ₂ )⁴ в законе Стефана - Больцмана представлено в виде T ₀ ⁴(1 + 40 ₂ ) , что ведет к погрешности

Q=LTA/R,

где L - постоянная Видемана-Франца, R -сопротивление контакта.

Анализ литературных данных и наши исследования показывают, что при напылении электронное охлаждение, нагрев легирующего газа, тепло диссоциации и сублимации и т.д. составляют менее 1% общего потока тепла.

При активизации процесса формирования покрытия лазерным излучением, происходит интенсификация процесса плазмохимического синтеза и дополнительный нагрев поверхности конденсации [2, 3].

Составляя уравнение теплового баланса на поверхности конденсации, получим:

не более 14% при Т₀=473 К и 0 ₂ < 0,5 .

Как уже отмечалось, в рассматриваемой области энергий доля отраженных и распыленных атомов мала, поэтому при энергии, достаточной для активации образования соединения и плотностях потока частиц порядка 1018-1022 ион/м2с, процесс роста покрытия будет лимитироваться только реиспарением [9-11]. Таким образом, скорость роста покрытия можно представить в виде

d Z dFo

mh

У 2 r 2 ^a 1

j - Ara +q )| ^: cxy V

в 1)

T <'- -q ) j JJ

, (22)

^д0 2 -    + Ki ^dZ

Ki + Ki,в₀ 0.

d ^           ¹ dF₀    ²

где константы А и В для различных материалов можно найти из [11].

Второй член в соотношении (22) имеет резко выраженную зависимость от температуры. Так, например при Т ₀ (1 +0 s) <600 К его вклад составляет доли процента от падающего потока частиц, поэтому в этой области

температур потоком реиспарения можно пренебречь. При больших температурах учтем влияние второго члена разложениеи его в ряд по величине 0<1, что дает:

Используя (15) и (16), получим:

Fo

где

в =

-у = в (1 - Bs s ),         (23)

dFo

9(°) + B j9«Дx)K(0,Fo - XW = fi JK(0,X)dX, k X 0                               k X 0

90) + B2 [9(Дx)K(0,Fo - XW = Z(0)(Ki - B9(0)) + k x 0

1 + —

k

Fo

J Ki_t(1 - B 3 6 ⁽⁰⁾) - Л ⁽⁰⁾

• X 0 _

дб (0) "

.   K (0, Fo - % ) dx .

^д X J

mh

Р 2^

(

1 - AT® ’ ⁵

exp -

B

т

T o

B 3 =

A ⁽ B -¹ " T

T 2 L-⁰— —l

■ 0,5

exp -

B

-

j - AT exp -

. T o В '

-

T

T ₀

Причем максимальное значение параметра в, например, для TiN составляет 3,32-10-4 при токе разряда катода 180 А.

Таким образом, тепловой аспект задачи ионно-плазменного напыления описывается системой уравнений (1) - (7), в которых Д Д, Д и в даются соотношениями (9), (21), (23).

Следует отметить, что при малых температурах потоком реиспарения частиц с поверхности можно пренебречь, тогда f (Fo) = Ki + ki.^-, d^- = в-2 1

dFo dFo

При более высоких температурах /, Д и в определяются из (21), (23), (24). Причем учитывая, что в^3,32-10 ^-4 , всегда можно ограничиться первыми двумя членами ряда. Первый случай нами был рассмотрен ранее в формулах (19) и (20).

Рассмотрим второй случай. Для этого разложим Z в ряд

га z=в£(Z(2n)в2n + z(2"°в). (25) n=0

Подставив (25) в (21) и (23), найдем:

d ? *⁰) dFo д 9 ⁽⁰⁾

= 1 - В₃ 9 ⁽⁰⁾ ,        = - В₃ 9 ⁽¹⁾ ,

³    ’dFo     ³

d ^

d 9 ⁽¹⁾ d ^

= Ki - В ₂ 9 ⁽⁰⁾ ,

Z

= Ki dFo

-

В ₂ 9 ⁽¹⁾ .

Применим к (25) преобразование Лапласа. Выделим 0(0) и выполнив обратное преобразование, придем к соотношению (19). Подставляя полученное соотношение в (24) и поступая аналогично, получим:

9 ⁽¹⁾ =

X

1 -

V

KiA ( 1 _ KAL Ki B 2 (     B 2 J B 2

KiB "

---3 +

B 2 J

Ki ² B

+---—

2 B

Fo

2 Ki J P( X , Fo - X ) d X +

T — -d-( ц D( ц )) ² x exp{ - ц ² Fo} t! Ц п L d ц

- ц = ц n

2 KiKi 1 B 3 k

X

где

T — -d"D 1 ²⁽ Ц ^)ex P ^{{ -} Ц ^{2 Fo}

S Ц п L d ц

I       ^                                \

P ( X , Fo - X ) =1 1 - T D (ц n )exp{ - Ц ² X} X

V n = 1                                      7

KiB. xj 0,5 +-----

I B 2

+² X IT ^{(1 k} X

V

KiB^ ^

B 2 J

+

B.Ki

+     T D2 (Цn) exp{-Цn2 X}T D2 (Цn) X k X n = 1                              n = 1

_k ²

X exp{-ц n2( Fo - X)} -   X k X

X 1 -

B Ki B Ki

—— + ——

B 2      B 2

j^ D(цn )exp{-Цn2 X} X n=1

^

XT D1(цn )cos цn exp{-цn2(Fo - X)}, n=1

ц n cos² ц n

-

^D 2 ⁽ ц n ) =

k 2     4

^cos ц n ^k X

0,5sin2 ц n + ц n

В связи с тем, что ряд процессов, происходящих при формировании покрытия определяется начальной стадией его образования, найдем выражения для температуры поверхности конденсации при малых Fo. Разлагая функции в соотношениях (25) и (26) в ряды по Fo и проводя необходимые преобразования, получим:

9 , =

2(Ki + p Ki^   о,5

-------FO kJn

( k.

•Ki ^ + в | — + ^k X         "

V

2 k

' X

B ₃ Ki 1 k X

1 1 1 + KB 3 e | Fo. ⁽²⁸⁾ k X

Как показывает анализ приведенных решений, при малых в распределение температур в такой системе определяется в основном теплофизическими параметрами и тепловыми условиями основы. С ростом в или Fo возрастает влияние кинетики наращивания на температуру. Скорость же роста покрытия зависит как от кинетики наращивания, так и от теплофизических коэффициентов и тепловых условий основы. При значении

Fo <

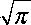
2( Ki + p Ki ) B ₃

скорость роста покрытия определяется в основном в.

Теоретические зависимости, полученные в настоящей работе, были использованы для разработки технологических режимов нагрева лазерным источником и нанесения покрытий из Ti, Zr и их нитридов на установке ионно-плазменного напыления Булат-1. В качестве лазерного источника использовался газовый СО₂-лазер "Латус-31".

Анализ экспериментальных измерений температуры системы и скорости роста покрытия и изменения температуры системы показал хорошую сходимость теоретических и экспериментальных результатов.

Так, при нагреве стальной пластины из материала ХН77ТЮР толщиной h=4-10^r3 м лазерным источником мощностью W=0,6 кВт, длиной волны Х=10,6 мкм и скоростью перемещения 0,2 м/мин и одновременным напылением на неё Ti на режиме I =130 A;

U=100 B, B=1,1 мТл, Р=266-10⁴ Па значение температуры, измеренное с помощью хро-мель-никелевой термопары в течение 300 с, изменилось от 373 до 435 К. Расчеты, проведенные по формуле (19), показали хорошую сходимость с экспериментом. При этом скорость роста покрытия имела постоянное значение 1,3-10^-8 м/с что отличалось от теоретического значения, рассчитанного по (23), на 15%.

Таким образом, полученное решение может быть использовано для расчета температур в системе при совместном воздействии лазерного и плазменного или ионно-плазменного источников нагрева. Предложенный метод позволяет также найти закон движения границы конденсации и установить области параметров, при которых возможно раздельное рассмотрение процессов движения фазовой границы и передачи тепла.