Нестационарная задача термоэлектроупругости для длинного пьезокерамического цилиндра

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2021PNRPU MECHANICS BULLETIN

В настоящее время пьезокерамические материалы используются при разработке датчиков температуры, работа которых основана на зависимости электрического поля, индуцируемого в пьезокерамическом элементе, от величины внешнего температурного воздействия [1–7]. Для расширения функциональных возможностей измерительных приборов данного типа возникает необходимость углубленного анализа нестационарных процессов, позволяющего понять эффект взаимодействия механических, температурных и электрических полей.

Математическая формулировка начально-краевых задач термоэлектроупругости включает систему несамосопряженных дифференциальных уравнений, исследование которых в последнее время, как правило, проводится при использовании численных методов [8–12]. Однако достаточно слабые эффекты взаимодействия полей различной физической природы удается проанализировать только с помощью замкнутых аналитических решений. При этом проблема интегрирования исходных расчетных соотношений и построение общего решения приводит к проведению расчетов в упрощенной постановке, а именно: исследуются несвязанные задачи [13,14] или анализируются бесконечно длинные тела [15–17].

Замкнутые решения динамических задач термоэлектроупругости представлены в немногих исследованиях [5, 14–17]. В работе [5] на основании известных характеристик вынужденных стационарных электро-упругих колебаний исследовалась плотность распределения температуры по длине конструкции. Статья [14] посвящена анализу напряженно-деформированного состояния длинного полого цилиндра в рамках LS-теории теплопроводности [18] при тепловом ударе без учета влияния электрического потенциала на термоупругие поля. В [15, 16] рассматриваются связанные задачи классической CTE-теории [19] для однородного и неоднородного пьезокерамических неограниченных слоев. Использование преобразования Лапласа позволило сформулировать в пространстве изображений интегральное уравнение Фредгольма, которое реализовывалось численным методом. В работе [17] предложена модель электротермоупругого полупространства с неоднородным покрытием, где для построения решения использовался численно-аналитический метод.

Можно отметить также работы [20–22], в которых используется нелинейная теория термоэлектроупругости, позволяющая описать отклик пьезокерамических конструкций с учетом неоднородных начальных условий.

Целью настоящей работы является решение связанной нестационарной задачи термоэлектроупругости для длинного полого пьезокерамического цилиндра при действии на его поверхностях температурной нагрузки и учете конвекционного теплообмена с окружающей средой [19] с использованием гиперболической LS-теории теплопроводности [18]. Рассматривается случай, когда скорость изменения нагрузки существенно меньше скорости распространения упругих волн, что позволяет не учитывать инерционные свойства конструкции и использовать в расчетах уравнения равновесия [23, 24].

1. Постановка задачи. Пусть полый длинный незакрепленный пьезокерамический цилиндр занимает в цилиндрической системе координат ( r , 0 , z ) область О : { a <  r <  b , 0 <0< 2 п , -то <  z < го } . Рассматривается случай действия на внутренней ( r = a ) цилиндрической поверхности нестационарной нагрузки в виде функции изменения температуры ю * ( t* ) (граничное условие 1-го рода), а на внешней ( r = b ) лицевой поверхности задан закон конвекционного теплообмена (граничное условие 3-го рода) и известна температура окружающей среды 3 * .

Внутренняя электродированная поверхность заземлена, а внешняя подключена к измерительному прибору с большим входным сопротивлением, что соответствует режиму электрического холостого хода.

В общем случае дифференциальные уравнения равновесия, электростатики и теплового баланса на основании гиперболической зависимости Лорда – Шульмана имеют вид [18, 25–27]

° 00

= r d_Ul _    _

C13     + C1    + e dr*

^Dr = ^e 33

дф *

--+ en dr    33

r *

- 31

дф * d r *

d и *

д ⁺ e 31 d r .

—

Y ii 0 * ,

U rv

— ⁺ g 3 ⁰ r _*

а объемная плотность энтропии s (r, t,) при разложе-_ „                           0*, нии в ряд Тейлора, с учетом условия —   1, опреде ляется зависимостью [15]

s = Y33Vи•+ k0--g3 дф-.(3)

Тo

В равенствах (2),(3) U * ( r , t* ) - радиальная составляющая векторов перемещений; ф * ( r , t* ) - потенциал электрического поля; С_тs , e_ms , е₃₃ - модули упругости, пьезомодули и коэффициент диэлектрической проница-

емости электроупругого материала ( m , s = 1,3 ) ; k -

ко-

эффициент объемной теплоемкости материала; y_tр у₃₃ компоненты тензора температурных напряжений; g

—

—

компонента тензора пирокоэффициентов; оператор

• V—А₊1 .

• d r *    r *

В результате подстановки (2), (3) в (1) получаем следующую систему дифференциальных уравнений термоэлектроупругости и краевые условия рассматриваемой задачи в безразмерной форме:

^ + ° rr °⁰⁰ = 0, V D — 0 ,         (1)

r

„ d U    U   бф     1 dф        0  .

V--a, —~ + V--a9---V0 + a9 — — 0, dr     r2     dr     r dr           r

d r *         r *

T T o

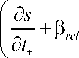
d ² 5 I    ~d0 *

—— l —ЛV--- , d t * ² J        d r *

dф      г U 1 d U         _n

-V — + a, V--+ a_s ---+ a, V0 = 0,

4               5                6

d r       dr     r d r

где °_r ( r , t* ), °₀ ( r , t* ) - компоненты тензора механических напряжений; D_r ( r , t *) - радиальная составляющая вектора индукции электрического поля; s ( r , t* ) - объемная плотность энтропии; 0 * = T - Т _о; 0 * , T , Т_о - соответственно приращение, текущая температура, а также температура первоначального состояния тела, при котором отсутствуют механические напряжения; р_ге/ - время релаксации; Л - коэффициент теплопроводности материала.

Уравнения осесимметричного состояния электро-упругой анизотропного среды при радиальной поляризации пьезокерамического материала с гексагональной кристаллической решеткой класса 6 mm записываются следующим образом [17, 27]:

° rr = C 33 ^U + C 13 — + - ^ - Y 33 0 * , (2) d r * r * d r *

Vd^-fl + p^l )f0 + a₇ v U - a ₈ дФ) = 0;

d r [d t d t² JI        ^{7         8} d r J

dU    U  dф _  .  .      ,_ r = R ,1 "Т;   + a9    + "7    0 = 0,  ф^ — R = 0 , 0|r — R = Ю1

dr      r

dф   d U   U)

--+ a,---+ as —+ a^ 0    = 0, 4             56

dr      dr      rJ.

d0 , „ I      _ A.

+ ^a 10 ⁰ l = ^a 10 ³ ;

^d r          J lr =1

т ±         d U dф d0 _ t = 0 U = ф = 0 = 0, --= — = — = 0 ;

^Y            d t    d t    d t

где

{ U , r , R } — { u * , r * , a } / b ,

{ 0 , « 1 , 3 } — ^33- { 0 * , ( ю * - T 0 ) , ( 3 * - T 0 ) } ,

C 33

ф—- e ³- Ф * , Cb

_ Л t —       t«, kb2 *

Ce ai = 7?" , a2 = —,

C ₃₃          e ₃₃

a ₃

- Y11  „ _   4

^—      ’ a 4

У зз           L 33 S 33

_ e 31 e 33       _ g 3 ^e33      _ ^Y33 Т 0

, a^              , a?

⁵     C 33 ^ 33     6    ^ 33 Y        7     C 33 k

^a8 ^—

У 33 g 3 Т 0 ek

a ₉

C

C ’

позволяет получить краевую задачу относительно функций u ( r , t ) , x ( r , t ) , L ( r , t ) с однородными граничными условиями:

V — — a и + ^ —a 1 ^l — vl + aL —R,(10)

dr 1 r2      dr    2 r dr

_ dx   ^5u    1 du

—V+ a ₄ V+ a, + a, V L — R ,

4   562

d r      d r     r d r

a₁₀ — a—, P — p,., —-, a - коэффициент теплоотдачи.

¹⁰      Л         re kb ²

Расчетные соотношения (5) учитывают отсутствие механических напряжений на цилиндрических поверхностях, заземление внутренней ( r — R ) и подключение к измерительному прибору внешней ( r — 1) электроди-рованных поверхностей, а также граничные условия теплопроводности.

С учетом заземления металлической подложки, напряжение холостого хода V ( t, ) определяется потенциалом электрического поля на внешней поверхности цилиндра:

V ( t . ) —ф ( 1, t . ) .                         (7)

2. Построение общего решения. На первом этапе решения выполняется процедура приведения расчетных соотношений (4)–(6) к виду, позволяющему в дальнейшем использовать метод конечных биортогональных интегральных преобразований [28]. Для этого вводятся новые функции u ( r , t ) , х ( r , t ) , L ( r , t ) связанные с U ( r , t ) , ф ( r , t ) , 0 ( r , t ) следующими соотношениями:

U ( r , t ) — H ( r , t ) + u ( r , t ) , ф ( r , t ) — H 2 ( r , t ) + x ( r , t ) , (8)

(S     Я²

V-- —+ P—7 I L + a ₇V u — a„ -^ I — R ;

d r  (d t    d t ² J(      ^{7       8} d r J ³

r — R ,1 | u + a 9 u + 1^ — L — 0, x _k — r —0, L r — r —0,  (11)

d r     r d r

(d L, Й

I+ a^L I — 0 , 15 ^r          )! r —1

t — 0 { u , X , L } —— { H 1 , H 2 , H 3 } , d { u , X , L } _: d { H 1 , H 2 , H 3 }

51                 51        ’ где

_     d H 1     H 1   ^5 H 2     1 d H 2

R, — —V--+ a. —- — V--+ a_?--- + V H^

¹         dr     ¹ r ²        dr

r dr

— a

H 3

, r

„  „ dH   „ dH,

R — V —² — a ₄ V —¹ — a₅ d r       dr

¹ d H ¹ — a ₆ V H 3 , r d r

R ——V^ H ³- + ⁽ —+ p-^^ | ⁽ H + a ₇V H.

³      d r U t  d t ² )( ³⁷¹

—

d H a ^{2 8} d r

где

{ H 1 , H 2 , H 3 } — { f ( r ) , f 2 ( r ) , f 3 ( r ) } _{Ю 1} ( t ) + + { f 4 ( r ) , f 5 ( r ) , f 6 ( r ) } 9 ,

Начально-краевую задачу (10)-(12) решаем, используя структурный алгоритм биортогонального конечного интегрального преобразования (КИП) [28]. Для этого вводим на сегменте [ R , 1] КИП с неизвестными компонентами собственных вектор-функций ядер преобразований K_v (X_z , r ) ... K ₃ ( X;, r ) , ^ ( ц_г, r ) ... N₃ ( ц_;, r ) :

G (X., t ) — jJ L ( r , t ) + a ₇V u ( r , t ) — a₈   X^ , ) K ( X , r ) rdr , (13)

‘                                                      d r )        i

Подстановка (8) в (4)–(6) при удовлетворении условий

dH1    H1  dH2       _ r — R, 1--+ aq--1---Ha — 0, dr    9 r    dr     3

r = 0

2| r — R    0,

3| r — R    ® 1 ’

d H d r

—

dH a4     1

d r

—

a

r

—

— 0,

5 H

—   + a10- dr

^{— a} 10 $

{ u ( r , t ) , x ( ^r , t ) , ^L ( ^r , t ) } ^— to

^— E ^G(Xi , t ) { N 1 ( ^ i , ^r ) , N 2 ( h i , ^r ) , N 3 ( h i , ^r ) } I I K - II , i — 1

II K - II² — J K 3 ( X , ., r ) N ₃ ( X , ., r ) rdr ,

R где X;, h — собственные значения соответствующих однородных линейных краевых задач относительно сопряженных Kk (X;,r) и инвариантных N (н,r) компонент вектор-функций ядер КИП (к —1,2,3).

В результате использования алгоритма КИП [22] получаем задачу для трансформанты G (X,-, t ) :

d ² G  dG   2

в —?—+---+ X G, — Rh , dt2 dt      i i H

t = 0 G t =o

dGi 0 , dt t=o

dG

"dt" ’

а также две системы дифференциальных уравнений, граничные условия относительно неизвестных компонент преобразований K (X,- , r ) ... K ( X,, r ) :

dK   K    dK

V —¹ - a, —³ + a. V —² - a, dr ¹ r ^{2    4} dr ⁵

¹ dK . -x 2 adK 3 = o r dr        dr

dK    dK    1 dK ₂

V--+ V--+ a,---+ X. a„ V K — 0, dr       dr 2 r dr i 8    3

r dr

dK  dK

V — ³ + —¹ + a₃ dr   dr

K 1 r

— a ₆ —² + X² K₃ — 0 ; 6                   i 3

dr

dK   K r — R ,1 —1 + a9 — + a4

dr      r

K

dK ² — X 2 a₇K₃ — 0 , i 7    3

dr

^K 2| r — R   ^K 3 r — R   ^{0 ,}

f dK  dK.

I--2 + —1

( dr dr

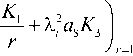
— 0,

+ a₂

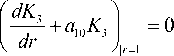
и N ( ц , r ) ... N з ( ц , r ) :

dN   N   dN

V — ¹ — a —1 + V — ² — a, dr ¹ r ²       dr ²

1 dN ₂            N ₃

---V N + a ₃ — — 0 , r dr        ^{3    3} r

dN ₂       dN ₁     1 dN ₁

—V--+ a. V--+ a,---+ a, VN3 — 0, dr 4 dr 5 r dr 63     ,

V —3 + ц2 N + a vN — a, i  3  71

dr      l

dN 2 )  ₀

dr )

dN   N  dN r — R,1--+ a91---N — 0, N,  » — 0 ,

9                        3             2| r—R dr      r dr

N 3| r — R — 0,                       (19)

5N2    5N1    N1

+ a,+ a^+ a, Nt—

4       563

dr       dr       r         /,

—^{3 + a} 10 N 3 dr

^ r — 1

— 0;

Задача для трансформанты G (14), (15) и сопряженная однородная задача (16), (17) относительно компонент ядра K ( X,, r ) ... K₃ ( X,, r ) получены в результате применения вырожденного преобразования (13), а соотношения (18),(19) построены путем применения к полученной (сопряженной) задаче (16),(17) аналогичного (13) КИП с компонентами ядра N ( ц , r ) ... N ₃ ( ц , r ) .

Общий интеграл уравнения (14) с учетом начальных условий (15) имеет вид

^G ( ^X i , ^t ) ^{— [в} ( m1 i — m 2 i ) ] ^{1 X}

^X M dG ⁰" ^{— TN} 2* I exP⁽ m1 ) ^{— в} I dT" ^{— TN} I i l exP⁽ m 2 1 ) ⁺ Il dt           )              l dt          )

t

+ j R H ( т ) { ехр [ m 1 , ( t — t ) ] — exp [ m 2 , ( t — t ) ] } d т ^ , (20)

0                                                                            J

где m_t,m_2l. — корни характеристического уравнения:

в m 2 + m. + X 2 — 0 .

В уравнении теплопроводности (10) перераспределение тепла в теле при малых значениях коэффициентов a ₇, a₈ происходит за счет учета скоростей изменения его объема и напряженности электрического поля. Это приводит к тому, что связанность термоупругих полей в большей степени оказывает влияние на трансформанту нагрузки G (X,-, t ) и незначительно - на форму функций K (X,- , r ) ... K (X,- , r ) , N ( ц , r ) ... N ₃ ( ц , r ) [23, 24]. Учитывая данный факт, при решении систем (16), (18) принимаем значения a₇ — a₈ — 0 и в результате получаем    следующие    выражения    функций

^К1 ( X i , r ) ... K 3 ( X i , r ) , N 1 ( ц , r ) ... N 3 ( ц , r ) :

K ^ ( X i , r ) — D_u + D 2i r A + D _{3 i} r ^— A ,          (21)

^K 2 ( ^X / , r ) ^{— D}1i a 11 ln ( r ) ⁺ D 2i^a12 r A ^{+ D}3i a 13 r — A ^{+ D}6i ,

K 3 ( X , , r ) — D 1i U 14 Q 00 ( X , r ) + D 2_A5 Q 0, a ( X , r ) + + D 3 , « 16 Q 0, — A ( X , r ) + D 4 , J 0 ( X , r ) + D 5, Y 0 ( X , r ) ,

^N 1 ( ц , ^r ) ^— EUr A ⁺ E 2 r ^— A ⁺ E 3 V , ,1 ( ^r ) ⁺ E 4 V ,2 ( ^r ) ⁺ E 5i^a17 , ^N 2 ( HP r ) ^— E 1 , a 18 r A ⁺ E 2, a 19 r — A ⁺

⁺ E 3,Vi ,3 ( ^r ) ⁺ E 4 , V ,4 ( ^r ) ⁺ E 5 , ^a 20 ^{ln( r} ) ⁺ E 6 , ,

^N 3 ( ц , ^r ) ^— E 3 ^J 0 ( h r ) ⁺ E 4 Y 0 ( h r ) ,

где R_H — — j ( RK + RK + RK ) rdr ,

R

G — — j(H1K1 + H2K2 + H3 K3 )t—0 rdr , R где

V,m (r) — ^ [rA j Fi,m (r )rAdr — rA j F,m (r )rAdr] (m —1,2), dG0 dt

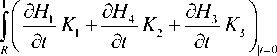
V , ,3 ( r H

dV , ,1 ( r )

a4      , dr

+ a₅r '^ _[( r ) + a₆J₀ (ц, r ) dr ,

V ,4 ( Г H

dVL2 (r)              \            \ a4     ,----+ a5r  V,2 (r) + a6Y0 (Pir)

dr

dr ,

F , m ^— ( 1 + a 4 ) - 1 ^X

\ Z 0 ^(p i r )          XZ ^ 0 ^(p i r )

(1 - a + a 2 a6 - a3 )--------+ (1 - a6 )----",---- r                dr m = 1    Zо (pr) = Jо (Pir), m = 2    Zо (pr) = Yo (pr),

A2 =(ax + a2a5)(1 + a4) 1, aH = -axa51, a12 = a2A 1 +1, a13 = a^A-1 -1, a14    (a a6 a + a ) , a15 — a2 a6  a + A (a6  1) , a, — aa - a - Ma, -1) , 16      2  6     3          6

a17 — a2 [(1  A ) (1 + a4 ) J  , a18 — a5A + a4 , a19 — a5 A-1 - a4, a20 — 1 + a5a17.

В равенствах (21) J _o (... ) , Y ( ... ) - обыкновенные функции Бесселя 1-го и 2-го родов нулевого порядка, Q _p( ... ) - неэлементарные функции Ломмеля ф — - A , 0, A ) [29], D_{x z}... D _6z., E_{x z}... E _6z. - постоянные интегрирования.

Подстановка K_x (X. , r ) ... K ₃ ( \ , r ) , N_x (p_z. , r ) ... N ( p_z., r ) в соответствующие граничные условия (17),(19) формирует две системы алгебраических уравнений, решение которых позволяет определить постоянные интегрирования D ... D , E ... E и собственные значения X , p_z.

Окончательные выражения функций U ( r , t ) , ф ( r , t ) , 0 ( r , t ) получим, применяя к трансформанте (20) формулы обращения (13). В результате, с учетом (8), имеем:

{и (r, t), ф( r, t), 0( r, t)} — {Н1 (r, t), H2 (r, t), H3 ( r, t)} + да

' X G (X„ t ) { N , ( p , r ) , N 2 ( p , r ) , N з ( p , r )}|| K i || . (22) i — 1

что позволяет существенно упростить правые части расчетных соотношений (10). В результате подстановки выражений H ... H в (23) формируются две системы уравнений относительно f ( r ) ... f ( r ) и f ( r ) ... f ₆ ( r ) . Их решение, при удовлетворении условий (9), позволяет определить функции H ... H .

3. Численный анализ результатов. В качестве примера рассматривается радиально поляризованный пьезокерамический цилиндр ( R — 0.8) состава ПКР-35, который для электроупругих материалов имеет относительно большой коэффициент линейного температурного расширения ( a_t —1.1 х 10^-5 K ^-1) [30]. В расчетах использовались следующие физические характеристики материала [30, 31, 32]: { q _п С ₃₃, С_{х 3}} — { 13.9, 11.8, 6.2 } х 10¹⁰ H/м², £₃₃ — 7.87х 10^-9 Ф/м, к — 4 х 10⁶ Дж/(м³ К), g₃ — 2х 10^-4 Кл/(м² К), { е_3рe ₃} — — { - 7.3,16.2 } Кл/м², {у,,,у₃₃} — { 2.93,2.43 } х 10⁶ Н/(м² К),

Л — 3.14 Вт/(м K), а — 5.6 Вт/(м² K), ₽_ге/ — 5 х 10^-6 с.

Рассматривается случай действия на внутренней поверхности ( r — a ) температурной нагрузки в виде

Полученные выражения являются сходящимися в силу полноты систем функций [ K_m ( X , r ) , N_m (p_z. , r ) ] ^ на интервале z g [ R ,1 ] .

Функции H ( r , t ) ... H₃ ( r , t ) определяются при решении следующих дифференциальных уравнений:

„d h   h. „а h,   1 a H _

-V — ¹ + a , -4-V — ² + a, --² + V H

23 r dr

d r

r

—

dr

aH — 0, (23) r

„ d H  „ d H

V —² - a. V — ¹ d r       d r

—

a ₅

1 ^d H 1                 а H 3

---a, v Н д — 0, v---- — 0.

r d r     ^{63      ,}      d r

® ; ( t . ) — T max [sin ( 9 1 . ) Н ( t max - t . ) + H ( t . - t ^ax ) ] ,     (24)

где H ( t ) - единичная функция Хэвисайда ( H ( t ) — 1 при t > ⁰ ,    H ( t ) ^{— 0} при t < ⁰ ),    T max ^— T ^ax ^- T 0 ,

T.v, t- максимальное значение внешнего темпера-max max турного воздействия и соответствующее ему время в размерной форме (T.ах — 373 K , T — 293 K), 9 — А"" .

2 t max

На рис. 1 представлены графики изменения функций 0 * ( r , t ) , ф ( r , t ) по радиальной координате r в различные моменты времени t ( b — 0.02 м, t *_ах — 1 с).

Цифрами 1–3 соответственно обозначены результаты, полученные при значениях t — t _max ,10 t _max ,100 t _max.

Анализ представленных графиков позволяет сделать следующие выводы:

• 1.    При достижении температурной нагрузки максимальных значений t — t _max (рис. 1, а, кривая 1 ) температурное поле изменяется в области, близкой с лицевой нагреваемой поверхности ( r — R ). В дальнейшем температурное поле цилиндра растет (рис. 1, а , кривая 2 ), и полный прогрев пьезокерамической конструкции наблюдается при t — 100 t _max (рис. 1, а , кривая 3 ).

• 2.    Наибольшие значения индуцируемого электрического поля ф ( r , t ) наблюдаются при достижении температурной нагрузки максимальных значений t — t_max (рис. 1, б , кривая 1 ). Далее, при постоянном значении

температурной нагрузки происходит уменьшение численных значений φ ( r , t ) (рис. 1, б , кривые 2 , 3 ).

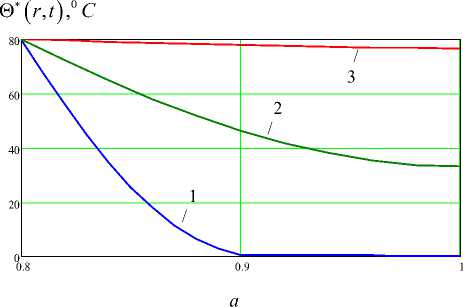
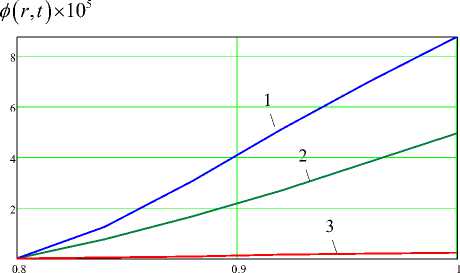
б

Рис. 1. Графики изменения функций    θ^∗ ( r , t ) , φ ( r , t )

по радиальной координате r в различные моменты времени: а – θ^∗ ( r , t ) ÷ r ; б – φ ( r , t ) ÷ r ( 1 – t = t _max ; 2 – t = 10 t _max ;

3 – t = 100 t _max , t _max = ^{Λ ∗} t _m ^∗ _ax) kb ²

Fig. 1. Graphs of changes in functions θ∗ (r,t),φ(r,t) along radial coordinate r at different moments: а – θ∗ (r,t) ÷r ; б – φ(r,t)÷r (1 – t=tmax; 2 – t =10tmax; 3 – t=100tmax, t max

= ^{Λ ∗} t ^∗ kb max

На рис. 2 показаны графики изменения перемещений U (1, t ) во времени t в случае достижения нагрузки максимальных значений за период время t ^∗= 10^-4 (с) ( t =1,33 ×10^-7 ). Сплошной и пунктирной линией соответственно обозначены результаты, полученные при использовании гиперболической и параболической ( β= 0 ) теорий теплопроводности.

Результаты расчета показывают, что при исследовании пьезокерамических радиально поляризованных цилиндров уточненную теорию Лоренца – Шульмана необходимо использовать при очень быстром изменении температурной нагрузки ( t ^∗≤ 10^-4 c). Это приводит увеличению перемещений до 10 % .

U ( 1, t ) ×10³

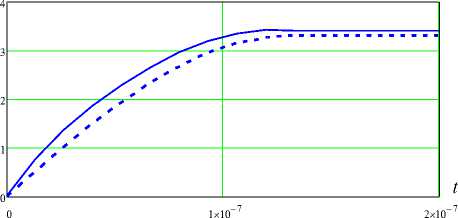
Рис. 2. Графики изменения функции U ( 1, t ) по времени t

Fig. 2. Graphs of function change U ( 1, t ) by time t

При этом необходимо дать оценку влияния сил инерции упругой системы на напряженно-деформированное состояние рассматриваемой конструкции при высокоскоростном температурном воздействии. Численные результаты расчета задачи электроупругости для длинного цилиндра [33] позволяют сделать вывод, что при гармоническом воздействии силы инерции необходимо учитывать при следующем соотношении частоты вынужденных колебаний ω и первой частоты собственных колебаний ψ : ^ω ≥ 0.5 . ^ψ

π

Принимая ω = θ = —7— и учитывая численные резуль-2tmax таты расчета, приведенные в работе [33], получаем, что при t∗≤ 10-5 данные характеристики оказывают влияние на деформированное состояние электроупругой системы. Таким образом, построенный алгоритм расчета, позволяющий учесть инерцию теплового потока, справедлив при 10-5≤ t∗ ≤ 10-4 (с).

На рис. 3, 4 представлены графики изменения температуры θ∗ ( r, t) по радиальной координате r и разности потенциалов V(t) во времени t . Сплошной и пунктирной линиями соответственно обозначены результаты, полученные с учетом и без учета скорости ∂ изменение объема электроупругого тела (  ∇U ).

∂ t

В настоящем примере при вычислении температурного поля θ∗ (r, t) и разности потенциалов V(t) наибольший эффект связанности наблюдается соответственно при t= 2t   и t= t . В дальнейшем данный эффект снижается.

Заключение. Полученные численные результаты позволяют сделать вывод, что при исследовании работы электроупругого цилиндра, выполненного из пьезокерамического материала с коэффициентом линейного температурного расширения α≥10-5K-1, необходимо учитывать связанность температурных и упругих полей. При этом вследствие различных скоростей распростра- нения электромагнитных и термоупругих полей можно не принимать во внимание влияние скорости изменения напряженности на температурное поле.

0"( r, t) ,0 С

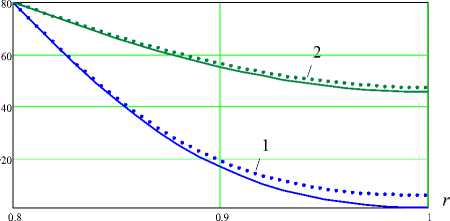
Рис. 3. Графики изменения ® * ( r , t ) по радиальной

V (t )x109

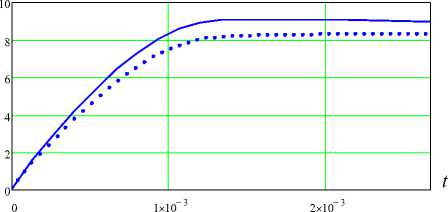
Рис. 4. Графики изменения разности потенциалов V (t) во времени t

Fig. 4. Graphs of difference in potentials V (t) within time t координате r в различные моменты времени

(1 –          ; 2 –)

maxmax

Fig. 3. Graphs of change ®*(r, t) along radial coordinate r at different moments (1 –        , 2 –)

max ,

Построенный алгоритм решения позволяет также учесть передачу тепла в виде теплового излучения. В этом случае нелинейное граничное условие теплопроводности 3-го рода удовлетворяется путем организации итерационного процесса.