Нестационарное четырёхволновое взаимодействие в прозрачной двухкомпонентной среде

Четырёхволновое взаимодействие может быть реализовано в средах с различными механизмами нелинейности, ответственными за изменение в среде под действием излучения комплексной диэлектрической проницаемости. В последние годы активно ведутся работы по исследованию четырёхволновых взаимодействий в многокомпонентных средах, в которых реализуются такие физические явления (и связанные с ними механизмы нелинейности), как термодиффузия, электрострикция, эффект Дюфура, обусловленные наличием растворённых частиц микро- и наноразмеров [1– 6]. Такие среды (суспензии, коллоидные растворы) благодаря высоким значениям их нелинейных показателей преломления могут использоваться в качестве нелинейных сред для низкоинтенсивного лазерного излучения в широком диапазоне длин волн [7, 8].

При исследовании четырёхволновых взаимодействий в многокомпонентных средах основное внимание, как правило, уделяется изучению энергетических характеристик (коэффициента отражения, дифракционной эффективности), разрабатываются методики определения кинетических коэффициентов нелинейной среды (коэффициентов диффузии, термодиффузии, Дюфура) [9–11], размеров микрочастиц [12, 13]. При этом вопросам, связанным с изучением пространственной селективности четырёхволновых преобразователей излучения в таких средах, уделяется меньшее внимание. При практическом же использовании преобразователей излучения в системах нелинейной адаптивной оптики, системах обработки и преобразования изображений, в которых взаимодействуют сложные пространственно модулированные волны, необходимо знать, насколько точно пространственный спектр волны с обращённым волновым фронтом (объектной волны) соответствует комплексно сопряжённому пространственному спектру сигнальной волны [14]. Точ- ность обращения волнового фронта определяет разрешающую способность таких систем.

К настоящему времени существует ряд работ, в которых для конкретных схем четырёхволновых взаимодействий в прозрачной двухкомпонентной среде исследованы пространственные, пространственно-временные характеристики четырёхволновых преобразователей излучения, осуществляющих обращение волнового фронта сигнальной волны [15– 18]. Представляет интерес построение единой нестационарной теории четырёхволнового взаимодействия в прозрачной двухкомпонентной среде, позволяющей проанализировать пространственно-временные характеристики четырёхволновых преобразователей излучения с учётом временной зависимости комплексных амплитуд взаимодействующих волн, геометрии взаимодействия, при наличии углового поворота и частотного сдвига волн накачки.

• 1.    Запись динамических решёток

Рассмотрим плоский слой оптически прозрачной двухкомпонентной среды (например, жидкость (газ) и наночастицы) толщиной ℓ , в котором распространяются волна накачки и сигнальная волна с амплитудами A 1 и A 3 и частотой ω 1 . Интерференция волны накачки и сигнальной волны приводит к изменению в пространстве интенсивности света. Вследствие явления электрострикции наличие градиента интенсивности приводит к возникновению потока концентрации наночастиц, который из-за эффекта Дюфура изменяет температуру. В результате, наводится решётка показателя преломления среды

5 n = f in 1 5 T+f in 1 5 C ( d T J C     ( d C J где δT и δC – изменения температуры и концентрации частиц.

Исходное скалярное стационарное волновое уравнение, описывающее распространение волн, есть

, 2 k ² . Y

V ² + k 1² + —^L 8 n I ( A 1 + A 3 + A 1 + A 3 ) = 0,       (1)

n 0     J

где k 1 = ® 1 n 0 /c , n ₀ - среднее значение показателя преломления среды.

Уравнение (1) дополняется системой материальных уравнений для изменений концентрации и температуры [15– 17]

С учётом изложенного выше из уравнения Гельмгольца (1) и материальных уравнений (2), (3) при ква-зиколлинеарной геометрии взаимодействия (волны распространяются под малыми углами к оси Z ) получим два схожих уравнения, описывающих изменение амплитуды волны накачки и пространственного спектра сигнальной волны

— = D22V28 C + yV21, d t cpv ^Ц = D11 V28 T + D12V28 C,

где I = AA ^*, D 11 , D 22 , D 12 и γ – коэффициенты теплопроводности, диффузии, Дюфура и электрострикции соответственно, c p – удельная теплоёмкость вещества, ν – плотность вещества.

В приближении заданного поля по волне накачки (| A 1 |>>| A 3 |) интенсивность излучения, распространяющегося в нелинейной среде, можно записать следующим образом

i = 1 ₀ + д а ; + a; A 3 ,

где I 0 = A 1 A 1 ^*.

Тогда изменения температуры и концентрации можно представить в виде суммы быстро (δ T 31 , δ C 31 ) и медленно (δ T 0 , δ C 0 ) меняющихся в зависимости от координат составляющих

^{d A} 1,3     k

—— + i — dz     n0

I ⁸ n I

I d T J _C

। ^ n ।

8 t + —

⁰ I d C J _T

8 C 0

A 1,3 = 0,

и два уравнения, описывающие изменения пространственных спектров концентрационной и температурной решёток

^d8 (C 31 (^K C , ^z , t ) = _D I _d2_ d t             ²² ( d z ²

-Y[(k1 z -k3z)2 + k2 ] A (z,t) A* (K3,z,t)x

X exp [i ( k1 z - k3z ) z ] , d8T31 (KT, z, t) _ cpV      dt"

Id ²

= D11\— -kT 18T31 (kt,z,t)+

Id z

I d2     2Y. -,F

^{+ D} 12 I 2Z ^{- - K} C I ^{8 C} 31 ^(K C , z , t ) ■

I d zJ

K _C I 8 C ₃₁ ( K _C , z , t ) -

8 T ( ^F , t ) = 8 T o ( F , t ) + 8 T 31 ( F , t ) + 8 T ^ ( F , t ) , 8 C ( ^F , t ) = 8 C ₀ ( ^F , t ) + 8 C ₃₁ ( ^F , t ) + 8 C 3*1 ( ^F , t ) .

Пусть волна накачки плоская, сигнальную волну разложим по плоским волнам

A ( ^F , t ) = A ( z , t ) exp ( - i K 1 P - i^ ^ z ) ,                (6)

M

A 3 ( r,t ) = J A ₃ ( K 3 , z , t ) exp ( - i к ₃ p- ik 3 _zz ) d K 3 ,     (7)

-M где A3 – пространственный спектр сигнальной волны, K13 и k 1>3z - поперечные и продольные составляющие волновых векторов первой волны накачки и сигнальной волны k1 3, F (p, z) - радиус-вектор, p (x, y) и z - поперечная и продольная составляющие радиус-вектора.

Быстро меняющиеся составляющие температуры и концентрации разложим по гармоническим решёткам

M

8 T ₃₁ ( ^F , t ) = J 8 T ₃₁ ( K _T , z , t ) exp ( - i K _T p ) d K _T ,

-M

M

8 C ₃₁ ( ^F , t ) = J 8 C ₃₁ ( K _C , z , t ) exp ( - i K _C p ) d K _C ,

-M где 8T31, 8C31 - пространственные спектры температурной и концентрационной решёток, KT , KC - волновые векторы соответствующих решёток.

При выполнении граничных

условий

V A 1 ( z = 0, t ) = 7 A 10 ( t ) , AL j ( K 3 , z = 0, t ) = V A 30 ( K 3 , t ) из (9)

имеем v41 (z, t) = 2A10 (t) exp [-P (z, t)], vA3 (K 3, z, t) = TA30 (K 3, t) exp [-P (z, t)],

где

P ( z , t ) = ^{ik L}j f I n J ^{8 T} 0 ( z j , t ) ⁺ fI n J ^{8 C} 0 ( z j , t ) d z ! ■ n ₀ • ^ 0 1 J _C           ^ о C J _T

При отсутствии потока частиц через грани нелинейного слоя и неизменности температуры на гранях, с учётом начальных условий 8 C ₃₁ ( к _C , z , t = 0 ) = 0 и 8 T ₃₁ ( K _T , z , t = 0 ) = 0 будем искать решение системы уравнений (10)–(11) в виде рядов Фурье

— I-           1 I-

^{8 C} 31 ^(к C , ^z , t ) = 2 ^C 0 ^(к C , t ) ⁺

M

+ E Cm (KC , t ) cos m=1

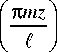
M

^{8 T} 31 (^K T , z , t ) = ^ ^Ts (^K T , t ) s = 1

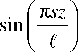
где C 0 , C m , T s – коэффициенты разложения рядов.

Подставив (13) в уравнения (10)–(11), найдём вначале изменение во времени пространственного спектра концентрационной решётки

8 C 31 ( к _с , z , t ) =

Y[ ^к C ⁺ ( k 1 z - ^k 3 z ) ² ]

= - i --------x----- ^x

( k1 z - k 3 z ) l

4 2 ( г,t ) = Я 2 ( z , t ) exp ( - ik ₂ r ) ,

^x J 4 (^T) 4 (^K 3 , ^T) ( { exp [ ^- i ( ^k 1 z ^- k 3 z ) ^l ] ^- 1 } ^x

M

x exp [-D22 кC (t -t)J - 2Z cos

x

m = 1

1 -(-1) m exp [-i ( k1 z - k 3 z ) lJ

n mz 1

--- x l J

1 -

n m    1

(k - k ₃ )l )

V X 1 z     3 z z )

x

где k 2 ( к 2 , k 2 _z ) - волновой вектор второй волны накачки, | k ₂| = k 2 = ю ₂ n ₀/ c , к 2 и k _{2 z} - поперечная и продольная составляющие волнового вектора k ₂ .

В результате дифракции второй волны накачки на решётке показателя преломления возникает объектная волна с обращённым волновым фронтом на частоте ω 2 с комплексной амплитудой A 4 .

Как и сигнальную волну, разложим объектную волну по плоским волнам

x exp ^- D 22

n m 1     ₂

-- +K 2

l J C

⁽ t ■ ^{d T}

^А4 ( ^? , t ) =

^

= J ^^ 4 ( к 4 , z , t ) exp ( - i к 4 p - ik 4 z, z ) d K 4 ,

-M

а затем изменение во времени пространственного спектра температурной решётки

^{8 T}31 ( ^к T , ^z , t )

= 2 i

YD12 [(k1 z - k3z )2 +KT 1

______L____________________=L x

^П c p ^V( k 1 z ^{- k} 3 z ) ^l

t

^ч . ( n sz 1 r ^x L sin I tLI ^ex P s = 1      ^{V l} ) 0

D cpv

П 5 1      2

-- +K 2 l )

(t-TR x

где A ₄ – пространственный спектр объектной волны, к 4 и k 4 _z - поперечная и продольная составляющие волнового вектора объектной волны k ₄ .

Рассмотрим схему четырёхволнового взаимодействия со встречными волнами накачки. При выполнении граничного условия А ₄ ( к ₄, z = l , t ) = 0 пространственный спектр объектной волны на передней грани нелинейного слоя и спектры температурной и концентрационной решёток связаны соотношением вида [16]

x

t

J А10 (T') 4 (к3, T')x

_          k

А 4 ( к 4 , z = 0, t ) = - 1 -2- А 20 ( t ) x n ₀

x

^к T { exp [ ^- i ( ^k 1 z ^{- k} 3 z ) ^l J ^- 1 } V

1 -(-1)s —-—— x

s

P ( l , t ) x ^k 4 z^k 1          J

xexp[-D22кT (t-t')J-

M

-z m=1

+ K T

1 -(-1)s+m 1 -(-1)s- m s + m s - m

^{1 -}(^{- 1} ) "  exp [" i ( k 1 z ^- k 3 z ) 7

x---------------------------x

1 -

n m    1

V ( k 1 z - k 3 z ) l)

A

x exp ^- D 22

П m 1      2 / zx , z ,

--- +к_т ( t-t ) d T d T .

l J ^{T (}       )

)

При выводе выражений (14)–(15) считали, что к _T = к _C = K 1 - к ₃. Эти выражения устанавливают однозначную связь между пространственными спектрами концентрационной, температурной решёток и спектром сигнальной волны.

2. Считывание динамических решёток

Будем считать, что динамические решётки считываются второй плоской волной накачки на частоте ω 2 с комплексной амплитудой A ₂

x exp

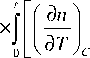
8 T 31 ( к t , z , t ) +

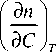
⁸ (C 31 (^к C , z , t ) exp [ ^- i ( ^k 2 z ^{- k} 4 z ) z J d z ,

где А 20 ( t ) = А 2 ( z = l , t ) .

Подставив (14), (15) в (18), получим выражение для временной зависимости пространственного спектра объектной волны

^4 (к4, z = 0, t) =

= ^А 20 ( t ) exp

^ P ( l , t ) k _{4 z}k ₁

x

x

t T

J J XT ( к4 , t - T, T - T') ^410 ( T') ^430 (к3, T')dT,dT + 00

t

+JXC (к4, t-T) А10 (T) А’0 (к3, T)dT

где

Xт (к4,t-т,т-т') =

2Y012к2 [(kiz - k3z )2 IKT ]   Г dn 1

cp Vn20 ( kiz — k3z ) ( k2z — k4z )2    V dT JC

^ { 1 ^-(^- 1 ) ^$ exp ^[- i ( к 2 z ^- к 4 z ) ¹ ] } ^X 5 = 1

X

-

V

П 5

1 -1

( k 2 z - k4 z ) l

exp

-

^D 11

J

^

Xexp[-О22кТ (т-т')]-5^

m = 1

c p ^v

( ^ j +K T ( t-т)> (к T {exp [-i ( k z - k 3 z )l] - 1} [1 -(-1) 5 ]

+ K T

1 -(-1)5+m

5 + m

₊ 1 - ( - 1 )

5 - m

X

X{1 - (-1)m exp [-i ( k 1 z - k3z ) l]}X

- 1

X exp ^- О 22

n m j ₂ — +к 2

l J

H

X C (^K 4 , t ^-т) =

Yk2 [кC +(k1 z - к3z )2 ] Г dn 1

i

n 0 ( k1 z - k 3 z )( k 2 z - k4 z ) l V d C J T

П m

(k - k w \\ 1 z 3z ) J

X

({exp [-i ( k1 z - k3z ) l] - 1}{1 - exp [-i ( k2z - k4z ) l]}X

^

Xexp [-О22кС (t -т)] + 2^{1 -(-1)” exp [-i (k1 z - k3z ) l]}{1 - (-1)” exp [-i (k2z - k4z ) l]}X m=1

X

nm

- 1

-

V

^{( k} 1 z ^{- k} 3 z ) ^l

nm

-.-----------2—

(k2 -k. )l

V 2z 4z 7

Как следует из выражений (20), (21), коэффициенты электрострикции, Дюфура не влияют на динамику пространственного спектра объектной волны. Временная зависимость пространственного спектра определяется коэффициентами теплопроводности и диффузии.

Выражения (18)–(21), записанные для четырёхволнового преобразователя излучения в схеме со встречными волнами накачки, могут быть обобщены на случай четырёхволнового преобразователя с попутными волнами накачки путём замены плоскости наблюдения пространственного спектра объектной волны с z= 0 на z= ℓ с учётом граничного условия на вторую волну накачки A 20 0 ( t ) = A 2 ( z = 0, t ) .

3. Обсуждение результатов

Исследование четырёхволнового взаимодействия в двухкомпонентной среде проводилось при условии Г ^{d n 1} _ Г ^{d n 1}

— oT >> — oC . Для типичных многокомпо-V d T J C V d C J T нентных сред, используемых в работах по четырёхволновому взаимодействию [7,8], это условие выполняется, как правило, при концентрации частиц менее 1012 см –3. В качестве сигнальной волны рассмотрим волну от непрерывного точечного источника, расположенного на передней грани нелинейного слоя

exp I- О 22

( A ₃₀ ( к ₃, t ) = 1 ) . Будем анализировать спектр объект-

ной волны в

k

1 z

k 3 z

к

к

2 k ₁

параксиальном приближении при неизменности во времени

амплитуд волн накачки ( A L 1_ ₂₀ ( t ) = /1 1,20 ) .

Геометрия распространения (встречная или попутная), угловой поворот, частотный сдвиг волн накачки меняют в выражениях (20), (21) разность проекций на ось Z волновых векторов второй волны накачки и объектной волны.

Так, в схеме со встречными волнами накачки

^k 2 z ^{- k} 4 z

_к 2 ₂

-

к

2 k ₂

а в схеме с попутными волнами накачки

2 z 4 z

к

-

к

2 k ₂

После интегрирования по временным переменным правой части выражения (19) с учётом (20) при распространении первой волны накачки строго вдоль оси Z ( к 1 = 0 ) получим

A4 (К 4, Z = 0, t ) =

² Y 0 12 k 2 [ ( k iz ^- k 3 z ) 2 + (^K 4 ^-К 2 ) ² ] ( g n A c p ^{V О} 22 n 20 ( k iz ^- k 3 z )( k 2 z ^- k 4 z ) 2 ^l 2 ^{V d T J} C

^A 10 ^A 20^exp

^P ( ^l ’ t ) k 4 z k 1

X

^X S { 1 ^-(^{- 1} ) ' exp ¹ i ( k 2 z ^- k 4 z ) ^l ] } 5 = 1

1 - exp

-

X

c p ^v

-

V

П 5

-1 -1

V

^D 11 c p ^v

I ( k 2 z

-

k 4 z )

J

^- k 3 z ) ¹ ] ^- 1 } ^{[ 1 -(- 1 ) 5} ] ^X

D 1

[{exp [-i ( kiz t Г exp I- О22 (К4

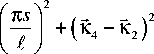
t

-

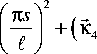
^К 2 ) ²

^D 11

^cp ^v

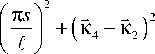
^{- О} 22 ^(K 4 ^-К 2 )

^

- 5 Z m=1

exp

-

1 -(-1)5+m 1 -(-1)5 - m

5 + m 5 - m

^{- О} 22

nm

I

+ (К 4

-

^D 11

П 5

+ (К 4

-

^{1 -}(^{- 1} ) m exP ^[- i ( ^k 1 z ^{- k} 3 z ) ^l ]

nm     |

( k1 z - k 3 z )1J

К ₂ ) ² t

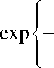
D 11

c p ^V

1 - exp

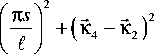
t

^К 2 ) ²

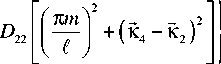
Выражение (24) записано при условии

К 1 + К 2 - К 3 - К 4 = 0.

Для стационарного режима ( t → ∞) пространственный спектр объектной волны есть

A4 (К4, z = I) =

i ^k 2 Y ^О 12 n ₀ D ₁₁ D ₂₂

( dn AV dTJ c

A 10 A 2 0 ^X

X exp

p ( i ) k 4 z k 1

2sh |к ₄ -К ₂| I

X

X({exp [- i (k1 z - k 3 z) I ] - exp (-|К 4 -К 2| I )}x

exp { ^[|^К 4 ^{- К} 2 I ^- i ( ^k 2 z ^{- k} 4 z ) ] ^l } ^{- 1}

X--Ft--T-i—T-----;—-— +| К4 -F - i ( k 2 z - k4 z )

⁺ { exp ^[- i ( k 1 z ^- k 3 z ) ¹ ] ^- exp (| ^К 4 ^-К 2, ¹ ) } ^X

exp {-[|К 4 -К 2I + i ( k 2 z - k4 z )] l}- 1

I К 4 -К 2| + i (k 2 z -k 4 z ) J

-iA-1 {exp (-iAi)-1}] , где A = (k 1 + k2 - k3 - k4)z - проекция волновой рас-

стройки на ось Z .

Выражение (25) обобщает представленное в работе [18] выражение для пространственного спектра объектной волны на случай квазивырожденного четырёхволнового взаимодействия в прозрачной двухкомпонентной среде с учётом поворота второй волны накачки.

^D 11

^cp ^v

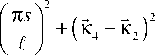
^D 11 c p ^V

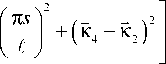
J

t r

Зависимость проекции волновой расстройки от поперечных составляющих волновых векторов взаимодействующих волн определяет общий вид пространственного спектра объектной волны, а явление электрострикции и эффект Дюфура – возникновение в амплитуде пространственного спектра провала, положение которого соответствует направлению распространения второй волны накачки [17].

Из материальных уравнений (2)–(3) следует, что при условии неизменности температуры на гранях нелинейного слоя с уменьшением пространственной частоты решётки (к _t ), амплитуда записываемой температурной решётки также уменьшается V ² 8 T ₃₁ ~ yV² A 1 A 3 * ~ к T и при к _T =0 равна нулю. Направление распространения объектной волны определяется условием фазового синхронизма, требованием равенства нулю поперечной составляющей волновой расстройки: К ₄ = К ₂ + К 1 - К ₃ = К ₂ + К _T . Таким образом, по мере уменьшения пространственной частоты записываемой решётки, направление распространения объектной волны начинает полностью определяться направлением распространения второй волны накачки, а её амплитуда, пропорциональная амплитуде записываемой температурной решётки, стремиться к нулю. Это и объясняет наличие провала в спектре объектной волны в направлении распространения второй волн накачки.

Введём безразмерный параметр, характеризующий нелинейную многокомпонентную среду b = c p v О ₂₂ О 1 ^- 11 . В случае среды, состоящей из воды, в

которой находятся наночастицы размером 10 ^–8 м, параметр b ≈ 2∙10^–5 [15].

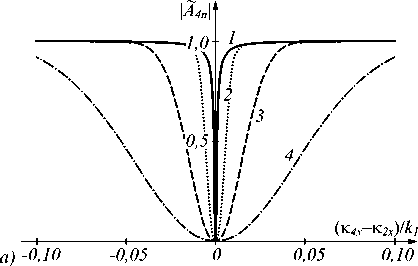
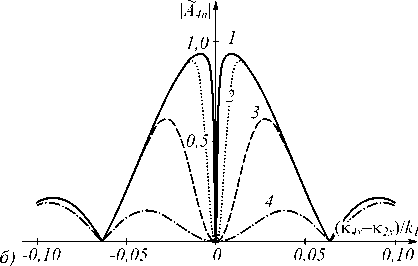
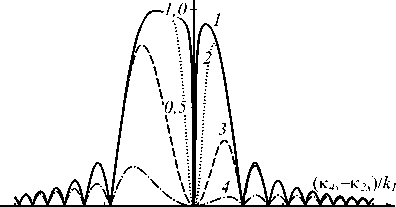
Будем считать, что волновые вектора волн накачки расположены в плоскости X Z, которую назовём плоскостью волн накачки. На рис. 1 в этой плоскости представлены характерные графики нормированных амплитуд пространственных спектров объектной волны (A4n ) в различные моменты времени при попутной (рис. 1в) и встречной геометриях распространения волн накачки (рис. 1а, б, г), при наличии углового поворота (рис. 1б) и частотного сдвига волн накачки (рис. 1г). Нормировка амплитуд пространственных спектров осуществлялась на значение ампли- туды спектра на пространственной частоте κ4 ≈ 0,1k1 при вырожденном четырёхволновом взаимодействии в схеме со встречными волнами накачки.

При равенстве волновой расстройки нулю (Δ ≡ 0, именно такая ситуация реализуется, например, при вырожденном четырёхволновом взаимодействии (ω1 = ω 2) в схеме с плоскими волнами накачки, распространяющимися строго навстречу друг другу (к 1 + К2 = 0)), четырёхволновой преобразователь из- лучения вырезает низкие пространственные частоты объектной волны. При этом высокие пространственные частоты преобразуются им с высокой эффективностью (рис. 1а).

|^4/?|

в)

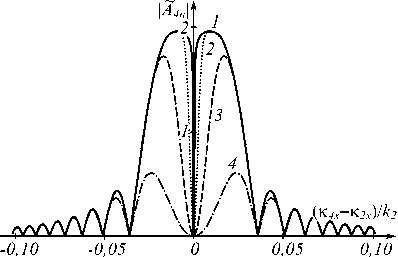
Рис. 1. Временная динамика пространственного спектра объектной волны в плоскости волн накачки при k₁ l = 5 - 10, b = 2 - 10 ^-5, k 2 /k i = 1 (а, б, в), 2 (г), к₂ х /k = 0 (а, г), 2 - 10 ^-2 (б, в), tD / 1 2 ) = 10 (1), 10 ^-3 (2), 10 ^- 4 (3),10 ^-5 (4)

Неравенство волновой расстройки нулю приводит не только к вырезанию в спектре объектной волны низких пространственных частот, но и к уменьшению эффективности преобразования высоких пространственных частот (рис. 1 б – г ).

С ростом пространственной частоты записываемой температурной решётки время выхода пространственного спектра на установившееся значение уменьшается [15], что является характерным для нелинейных сред с тепловой, диффузионной нелинейностями [14, 19]. Это объясняет совпадение на рис. 1 пространственных спектров в различные моменты времени, начиная с некоторой пространственной частоты, величина которой со временем уменьшается, выходя на постоянное значение. Такую частоту можно определить по фиксированному относительному отклонению амплитуды пространственного спектра в произвольный момент времени от значения амплитуды пространственного спектра для стационарного режима.

Для характеристики пространственной селективности четырёхволнового преобразователя в плоскости волн накачки введём ширину полосы вырезаемых пространственных частот (Δκ) и ширину полосы наиболее эффективно преобразуемых частот (Δκ e )

Ак( t ) = 2 (к41 -^ x), (26)

^АК e ( t ) = |^К 42 ^К 41|, ⁽²⁷⁾ где к ₄₁₂ =|к ₄₁₂| - пространственные частоты, значения которых находятся из решения уравнения

| A 4 ( К 41,2 , z = 0, t )| = 2 A 4max ( t ) , (28) гДе ^A 4max ( t ) = | A 4 (^K 4 = ^K max , Z = 0, t )| ^- наибольшее значение амплитуды пространственного спектра, к ₄ = | К ₄1, к_тах - пространственная частота, на которой пространственный спектр достигает наибольшего значения, κ 2 x < κ 41 < κ max , κ 42 > κ max .

Поворот волны накачки (рис. 1 б , в ) приводит к нарушению осевой симметрии в пространственном спектре объектной волны ( A ₄( к 4 , t ) ^ A 4 ( -к 4 , t )), наблюдаемой на рис. 1 а , г .

С течением времени ширина полосы вырезаемых пространственных частот Δκ монотонно уменьшается (рис. 2, кривая 1). Ширина полосы наиболее эффективно преобразуемых частот Δκ e в противоположность аналогичной зависимости для четырёхволнового преобразователя излучения в среде с тепловой нелинейностью [19] с течением времени увеличивается (рис. 2, кривая 2).

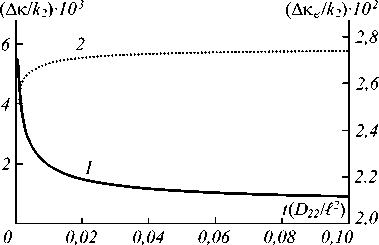
Рис. 2. Временная зависимость ширин полос вырезаемых (1) и наиболее эффективно преобразуемых (2) пространственных частот объектной волны при четырёхволновом взаимодействии в схеме со встречными волнами накачки при k 1 ℓ = 5 ⋅ 10³, b = 2 ⋅ 10 ^–5, κ 2x / k 2 = 0, k 2 / k 1 = 2

Как Δκ, так и Δκ _e со временем выходят на стационарные значения Δκ^∞ и ∆κ _e ^∞ соответственно. Рост параметра b (коэффициент теплопроводности уменьшается) приводит к замедлению выхода ширин полос пространственных частот на стационарные значения. Значения Δκ^∞ и ∆κ _e ^∞ не зависят от «тепловых», элек-трострикционного параметров нелинейной среды, определяются только её толщиной, значением волновых чисел и угловым поворотом волн накачки.

Заключение

Для четырёхволнового преобразователя излучения в прозрачной двухкомпонентной среде получено аналитическое выражение, устанавливающее однозначную связь между временной зависимостью пространственного спектра объектной волны и временными зависимостями амплитуд волн накачки, пространственным спектром сигнальной волны. Показано, что зависимость проекции волновой расстройки от поперечных составляющих волновых векторов взаимодействующих волн определяет общий вид пространственного спектра объектной волны, а явление электрострикции и эффект Дюфура – возникновение в амплитуде пространственного спектра провала, положение которого соответствует направлению распространения второй волны накачки. Временная зависимость пространственного спектра определяется коэффициентами теплопроводности и диффузии и не зависит от коэффициентов электрострикции и Дюфура. C течением времени, выходя на стационарные значения, ширина полосы вырезаемых пространственных частот монотонно уменьшается, а ширина полосы наиболее эффективно преобразуемых частот увеличивается.