Нестационарные колебания ролика, контактирующего с твердой поверхностью, при наличии смазочного слоя
Автор: Иванов В.А., Еркаев Н.В.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 1 т.18, 2017 года.
Бесплатный доступ
Получено аналитическое решение задачи нестационарного гидродинамического контакта ролика с твердой поверхностью в присутствии жидкого смазочного материала. Данная задача является актуальной и важной, так как нестационарный режим в подшипниках преобладает при стартах космических аппаратов. Распределение давления вдоль смазочного слоя получено в результате интегрирования уравнения Рейнольдса с учетом как тангенциальной, так и нормальной скорости ролика относительно опорной поверхности. Интегрированием давления вдоль поверхности контакта определена нормальная сила, действующая на ролик со стороны смазочного слоя и называемая несущей способностью слоя. Показана линейная зависимость несущей способности от нормальной скорости ролика по отношению к поверхности контакта. Определен коэффициент демпфирования смазочного слоя, являющийся коэффициентом пропорциональности между усилением несущей способности и величиной нормальной скорости. Для нормальных колебаний ролика получено обыкновенное дифференциальное уравнение с малым параметром при старшей производной. Решение этого уравнения, называемого жестким, представлено в виде асимптотического разложения по сингулярному малому параметру. Получены выражения для нулевых и линейных членов разложения, содержащих как регулярные, так и погранслойные функции, затухающие с течением времени. Показано, что процесс установления характеризуется двумя временными масштабами. Первый масштаб определяет резкий рост максимума давления сразу после скачка нагрузки. Второй - отражает процесс плавной релаксации давления к стационарному значению, соответствующему возросшему значению нагрузки. Полученные результаты обосновывают важность учета нестационарных переходных процессов в узлах трения летательных аппаратов. Если при медленном (квазистационарном) возрастании нагрузки в 2 раза максимальное по слою давление испытывает примерно двукратное увеличение, то в результате аналогичного по величине, но внезапного скачка нагрузки максимальное по слою давление во время переходного процесса кратковременно возрастает более чем на порядок. Такой значительный и резкий скачок давления в смазочном слое может критически отразиться на ресурсе всего узла трения.
Смазочный слой, гидродинамическая смазка, колебания ролика, асимптотическое разложение
Короткий адрес: https://sciup.org/148177689
IDR: 148177689 | УДК: 628.822
Текст научной статьи Нестационарные колебания ролика, контактирующего с твердой поверхностью, при наличии смазочного слоя
Введение. Стационарная гидродинамическая задача контакта ролика с пластиной при наличии смазочного слоя, разделяющего поверхности, рассматривалась во многих публикациях [1–5] и достаточно хорошо изучена. В то же время нестационарные аспекты гидродинамического контакта ролика с твердой поверхностью остаются в значительной мере неисследованными. Эта тема важна и актуальна, так как именно нестационарный контакт свойственен роликоподшипникам, работающим при переменных нагрузках, которые возникают при стартах космических аппаратов. При такой работе подшипников происходят быстрые изменения зазоров между контактирующими телами, сопровождающиеся значительным ростом вертикальных скоростей, которые, в свою очередь, приводят к резкому росту пиковых значений давления в смазочном слое.
В данной статье рассматривается асимптотический аналитический метод [6–8] решения нестационарной гидродинамической задачи с применением коэффициента демпфирования смазочного слоя.
Схема контактного взаимодействия цилиндрического ролика с твердой поверхностью, покрытой слоем смазочного материала, представлена на рис. 1.
где P – давление в смазочном слое; V – тангенциальная скорость ролика относительно поверхности; ц - динамическая вязкость масла при нормальном давлении; h – толщина смазочного слоя, зависящая от деформации поверхностей. Ось x ориентирована вдоль поверхности контакта, как показано на рис. 1. Здесь используется система отсчета, в которой ролик имеет нулевую тангенциальную скорость, а поверхность, соответственно, движется в направлении X .
В предположении, что площадка контакта цилиндра и плоскости мала по сравнению с радиусом кривизны R , имеем следующее выражение для толщины слоя смазочного материала [2]:
h = h m + ( X - X m ) 2 / ( 2 R ) , (2)
где h m – минимальная толщина смазочного слоя; x m –
координата точки минимального зазора.
Граничные условия в рассматриваемом случае имеют следующий вид [2]:
P ( X 1 ) = P ( X 2 ) = dX ( X 2 ) = 0,
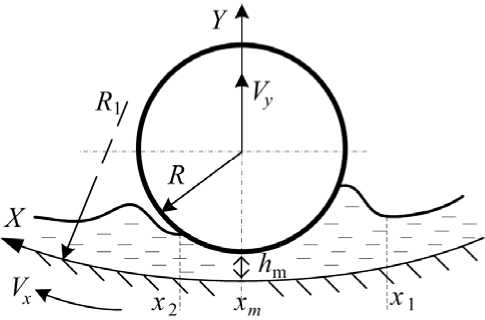
Рис. 1. Схема расположения ролика и слоя жидкого смазочного материала
где x 1 и x 2 – входная и выходная границы смазочного слоя.
Для удобства решения задачи вводим безразмерные переменные:
X = ( X - X m )/Jh m R,
q = Ph^/ (6 ц v4r ),
= V y К
Vhm .
Используя (4), преобразуем исходное уравнение
Рейнольдса (1) к более простому виду:
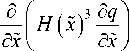
ah ( ~x )
a x
+ 2 u ,
H ( X ) = 1 + X 2 /2.
Расчет давления в смазочном слое. Рассмотрим идеализированную модель контакта ролика с поверхностью при постоянном коэффициенте вязкости в смазочном слое [9; 10]. В этом случае распределение давления определяется из уравнения Рейнольдса [11]:
af,3a p ( a h 2 a h ^
— I h3 — 1 = 6 ц V I- +--I , d x ^ a x J ^ a x v d t J
Положения входной и выходной границ будем характеризовать безразмерными параметрами a и c . Значение параметра a зависит от количества смазки. В случае обильной смазки полагаем a = -да [2; 3; 12].
Интегрируя уравнение (5) и используя нулевое граничное условие (3) для производной функции давления при x = c , получаем дифференциальное уравнение первого порядка:
5 q _ H ( x ) - H ( c ) 2 e ( X - c ) d X H ( X ) 3 H ( X ) 3
_ ( x - c ) /2 2 u ( x — c ) ( 1 + X 2 /2 ) 3 ( 1 + X 2 /2 ) 3
Для перехода к размерному виду используем зависимость
W _ W ' 6 ^ VR .
0 h
Решение уравнения (6) зависит от безразмерного параметра υ, который связан с нормальной скоростью перемещения ролика. Интегрируя уравнение (6) для различных значений υ, находим распределение давления в смазочном слое с учетом нормальной скорости ролика (рис. 2):
' 2 X ( с 2 (3X2 +10)-2 X 2 + 4) ^^^^^^B ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^B ^^^H
1 (x 2 + 2)2
q ( X )_ 16 ' ) +
-V2 (3 с 2 - 2)tg-1 (- x ^
С учетом соотношений (4) и (10), преобразуем выражение (9) к размерному виду:
6 ц VR 6 ц R 3/2
W _ W + A ^- V . . (11)
h m hm 3/2
Здесь первое слагаемое выражает зависимость стационарной несущей способности от зазора при нулевой нормальной скорости, а второе слагаемое учитывает влияние нормальной компоненты скорости. Коэффициент перед скоростью будем называть коэффициентом демпфирования X :
X_ A
6 ц R 3/2
20 cX 3 + 3л/2 c ( X 2 + 2 ) arctan I - x | + 20 cX + 16
+----------------------------------------- 2 u .
3/2 m
.
Исследование нестационарного процесса. Для исследования нестационарного процесса запишем уравнение движения ролика по нормали к поверхности:
Определение коэффициента демпфирования смазочного слоя. По найденным распределениям давления определяем значения несущей способности, являющейся функцией параметра υ:
mdh m + X ( hm ) dh m - W 0 ( hm ) _- F , (13)
dt 2 dt
-
c
W ' ( u ) _ J q ( x , u ) dX . (8)
-
a
где m – масса ролика; F – внешняя нагрузка.
С учетом зависимостей (11) и (12) уравнение (13) принимает следующий вид:
Согласно формуле (7), давление линейно зависит от параметра υ, поэтому несущую способность также представим в виде линейной функции следующего вида:
d2hm 6цR3/2 dhm 6ц VR m + A W 0
dt 2 hm 3/2 dt hm
- F . (14)
W ‘_ W 0 ' + A u , (9)
где постоянные коэффициенты W и A равны 0,401 и 1,125 соответственно.
Полагая равными нулю производные по времени, определяем равновесное значение зазора:
h 0 _
6 ц VRW 0 F
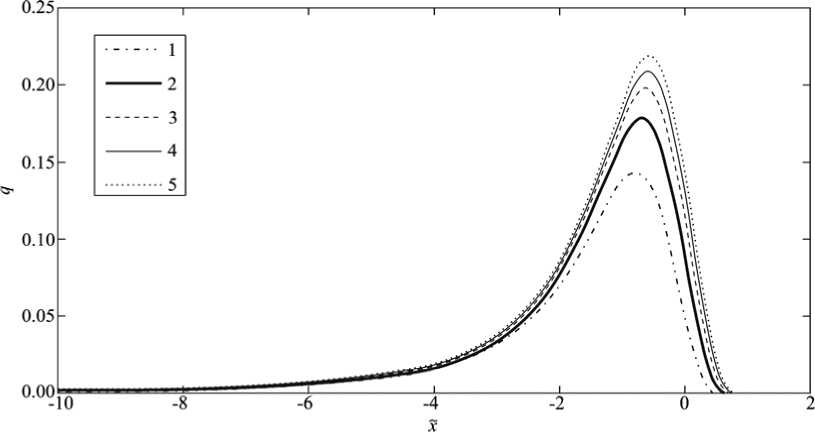
Рис. 2. Безразмерное распределение давления в смазочном слое при разных υ:
1 – υ = +0,1; 2 – υ = +0,05; 3 – υ = 0; 4 – υ = –0,05; 5 – υ = –0,1
Принимая h 0 в качестве базового зазора, вводим безразмерные переменные:
A Rh hm = h'ho , t = tto, tо = VW,,.
Используя нормировки (16), приводим уравнение динамики к безразмерному виду:
11 . „
£h‘ + h‘ h‘-h1 = 0(17)
mV 2 W [2
£ = —Y--
A 2 FR
Уравнение (17) определяет зависимость зазора от времени в процессе установления стационарного режима. Характерное время переходного процесса определяется параметром 1 0.
Зададим начальные условия при t = 0:
h (0) = h m / h о - h o\ h (0) = 0. (18)
Интегрируя уравнение (22), получаем:
h 0 ( t ') =
|
У 2 |
||
|
e |
уК±1 |
+ 1 |
|
V h 0* - 1 |
||
|
У h 0 + 1 |
- 1 |
|
|
e |
||
|
V |
У h 0* - 1 |
J |
Функция (25) удовлетворяет начальному условию h (0), но дает ненулевую начальную скорость:
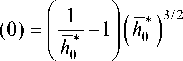
Для компенсации этой скорости далее вводится погранслойное решение.
Далее переходим к определению второго члена регулярной части асимптотики. Для этого преобразуем уравнение (23) к виду
Так как параметр e при старшей производной является малым, то уравнение называется жестким [13], и его решение может быть приближенно представлено в виде асимптотического разложения по сингулярному малому параметру [14; 15]:
h ‘ = h ( t ‘ , £ ) + Л( т , £ ), т — t' / £ ,
- 72 h'+ З^ hA - ^ h‘= h0, h 0 2 h 0
где h0 =(1 - h0) .(28)
где первое слагаемое
h ( t ‘ , e ) = h , ( t ‘ ) + e h 1 ( t ‘ ) + ... + £ khk ( t ‘ ) + ...
Подставляя (28) в (27) и выполняя алгебраические преобразования, получаем:
является регулярной частью асимптотики, а второе слагаемое hl (т, £) = h0(T) + £ h^l) + ... + £ k hlk (т) + ...
представляет собой сингулярную часть асимптотики, называемую также в литературе погранслойной асимптотикой. На пограничные функции накладываются дополнительные граничные условия затухания hk (т) ^ 0, т^®. (19)
1 — h1 +--/=^(3h0 -1) h = -h0h0 . (29)
2 A
Введем замену:
- dh, h, = —1 dt
dh 1 dh 0 dh 1 —
—=--° = h0, dh 0 dt dh 0
—— dh 0 - 1 dh0 2 h hn .
dh 0 0 2 dh0
Подставляя (30) в (29), получим следующее выражение:
Для первых членов асимптотики имеем выражения h ‘ — h0 (t) + e h1( t) + e h1(т), (20)
d=-h0 + (3h0 - 1)h 1 = dh0 2д/ h0
• • • h = h 0( t) + eh1( t) + e h1(т). (21)
Уравнения на функции регулярной и погранслой-ной частей асимптотики можно получить путем подстановки выражения (14) в уравнение колебаний (17), группировки членов с одинаковыми степенями малого параметра и приравнивая к нулю. В результате получаем следующую систему уравнений:
1 - X dh - 1 = 0. h 0 h0 3/2 dt ‘
^ 7 + ( 3 h 0 - 1 ) = - h 0 , (23)
dt 27 h o
2,~ d2 h 1 dh Л
—4- ■ --- . —1 = 0
d т 2 h 0(0)3/2 d т
dh 0 —
= h 0 h 0
dh 0
Следовательно,
1 d h 0 h 3/2
2 dh0 °
0 2 — ( 1 - h )( 1 - 2 h ) . (32)
dh 0 ' M '
Выражение (31) с учетом (32) примет вид dh1 ^ho (1 - h0) + (3h0 -1) h1 — dh 0 2 ^h 0
-
— - 2 ( 1 - h )( 1 - 2 h 0 ) h (33)
Разделив уравнение (33) на коэффициент при старшей производной, получим дифференциальное уравнение следующего вида:
dh i + X M h dh 0 2 h 0 ( 1 - h 0 )
- 2 ( 1 - 2 h o ) h 0 .
1 т V h 0+1 — Ln ^4=—
2 hh- -1
+ — Ln
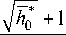
- 1
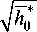
+ C 0
Общим решением уравнения (34) является функция
h 1 = G ( h 0)exp
1 h 0 ( 3 s - 1 ) 2 1 s ( 1 - s )
h 0
ds
Преобразуем подынтегральное выражение:
2 h * h0 ( 1 s )
Г 1 1 h
= 2 In s + ln(1 - s )
2 s 1 - s
- h 0 '
, (1 - h 0 ) ¥0
= In ----^
h 0
h 0 *
Тогда уравнение (35) с учетом (36) примет вид
(1 -h0 )Nh h1 = G(h0) = G(h0)(1 h0 )' h0 ,
(1 - h 0)V h
где G – неизвестная функция, определяющаяся интег-
рированием следующего уравнения:
dG ( h 0) __1 ( 1 - 2 h 0 ) ^0 dh = 2 ( 1 - h 0 )
Вычисляя интеграл, находим
G ( h 0 ) = - 1f s + C 0 =
2 ( 1 - s )
h 0
h 0 1 h 0 s
= - f s/dds + — I"---- ds + C 0. (39)
•. 2 •. 1 - s h0h0
В подынтегральном выражении второго слагаемого уравнения (39) применяем замену переменных u = s[s и выполняем алгебраические преобразования:
su 2
ds—ds = 2 --- ddu =
J1 - s J1 - u 2
= " 1 du - " —^—du - 2 " du . (40)
J u + 1 J u - 1 J
Интегрируя (40) и производя обратную замену переменных, получим выражение:
3/2
G ( h 0) = — h3/2 + - (h0 + J h 0 -
03030 0
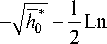
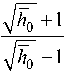
T T h 0* + 1
Ln *
V h 0 - 1
+ C 0 . (41)
С учетом уравнения (41) уравнение (37) примет вид
h 1 = ( 1 - h ) \h
I
- 3 h3/2+3 (h0) + Th0- hK-
\
Далее, интегрируя уравнение (24) с учетом условия затухания при т ^ да , получаем выражение
dh- = C 1exp ( -т /( h 0' )3/2 ) . (43)
d т х '
Постоянная интегрирования С 1 определяется из условия нулевой начальной скорости для полного решения, представляющего собой сумму регулярной и погранслойной асимптотик. Так как первый член регулярной асимптотики дает ненулевое начальное
значение скорости dh 0 dt
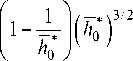
то подбираем постоянную С 1 таким образом, чтобы погранслойное решение компенсировало значение (26)
при т = 0:
I 1
C1 = -1 (h 0) .
Ih 0
Подставляя найденное значение в выражение (44) и повторно интегрируя, находим выражение погранс-лойной части асимптотики:
r h1 =-( ho - 1) ThT exp
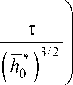
*3/2
( h 0 )
+ C 2 .
Константа C 2 подбирается таким образом, чтобы решение удовлетворяло нулевому граничному условию при т ^ да ( С 2 = 0).
Найденная погранслойная функция дает ненулевое возмущение в начальный момент времени, которое можно скомпенсировать подбором постоянной интегрирования C 0 в выражении второго члена регулярной асимптотики:
С 0 = ( 1 - h 0 ( t ) ) T h¥
( h ^y ( 1 - h *) У
В результате итоговое выражение принимает вид:
\
3/2 2* 3/2
* -3 ( h ) -’
гтт~ 1 т T h cC t )+1
- hht) t ) + hh 0 + J-11- — 2 W t ) - 1
1Ln 2
*
V h +1
УТ - 1 J
+
, _ . ( h ' ) h ' -11
+ ( 1 - h ( t ) ) У J . (48)
(1 - h 0 ) A
После определения всех функций регулярной и погранслойной частей асимптотики уравнения (20) построим график зависимости зазора от времени для различных начальных значений (рис. 3).
Рис. 3 показывает, что после любого внезапного скачка нагрузки, который характеризуется безразмерным
параметром h ′(0), величина зазора стремится к новому равновесному значению. При этом скорость изменения зазора тем больше, чем больше начальное отклонение зазора от равновесного значения. На рис. 4 представлен график изменения относительной скорости сближения поверхностей между контактирующими телами со временем для начального условия h ′(0) = 2.
Рис. 4 показывает, что увеличение параметра ε приводит к более плавному изменению вертикальной скорости ( dh′/dt′ ). При этом для очень малых значений ε скорость изменения зазора возрастает практически мгновенно, что в свою очередь вызывает резкий и большой скачок давления.
Зная зависимость зазора от времени, построим график изменения максимума давления (рис. 5).
Из рис. 5 видно, что процесс установления можно охарактеризовать двумя временными интервалами. На первом интервале отмечается очень быстрый рост давления. Амплитуда и длительность роста давления определяется параметром ε. Чем меньше малый параметр ε, тем быстрее увеличивается со временем давление в смазочном слое. На втором временном интервале происходит процесс плавного спада давления к стационарному значению, соответствующему установившемуся состоянию смазочного слоя при постоянной нагрузке. На рис. 6 представлен график нелинейной зависимости пикового значения давления от величины начального зазора, отнесенного к равновесному значению. Данный график показывает, что чем больше малый параметр ε и чем больше отклонение от равновесного зазора, тем сильнее проявляется нелинейность увеличения пикового давления. Величина hm/h0 обратно пропорциональна скачку внешней нагрузки (отношению действующих сил F1/F0).
Рис. 5 и 6 показывают, насколько важно учитывать нестационарные переходные процессы в узлах трения летательных аппаратов. Например, при медленном (квазистационарном) увеличении нагрузки в 2 раза максимальное по слою давление увеличивается в 2,2 раза. Однако после внезапного скачка нагрузки в 2 раза во время переходного процесса максимальное по слою давление кратковременно возрастает в 13 раз. Такой резкий скачок давления в смазочном слое между контактирующими поверхностями критически сказывается на ресурсе всего узла трения.
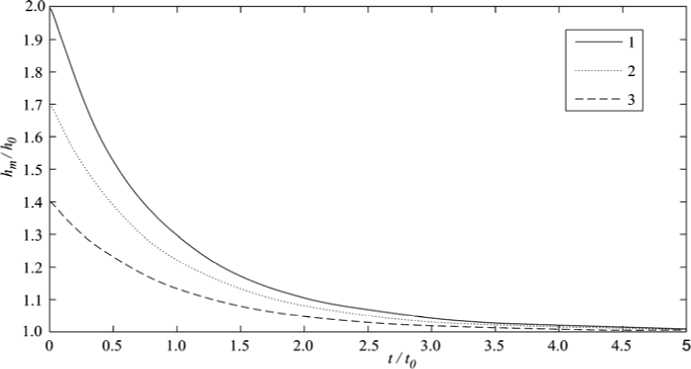
Рис. 3. Зависимость зазора от времени при ε = 0,01 для различных начальных условий: 1 – h ′(0) = 2; 2 – h ′(0) = 1,7; 3 – h ′(0) = 1,4
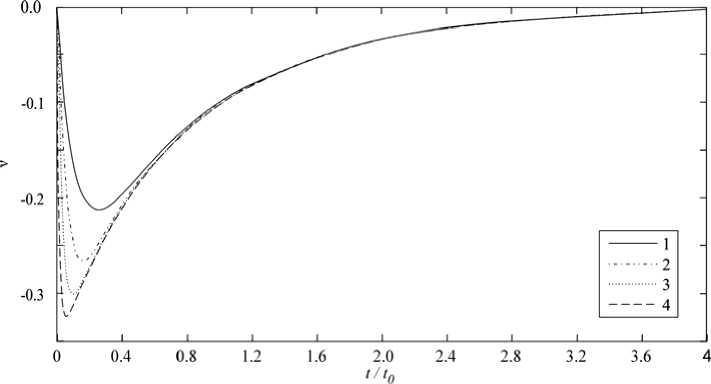
Рис. 4. Относительная скорость изменения зазора при начальном условии h ′(0) = 2 для различных значений малого параметра:
1 – ε = 0,04; 2 – ε = 0,02; 3 – ε = 0,01; 4 – ε = 0,005
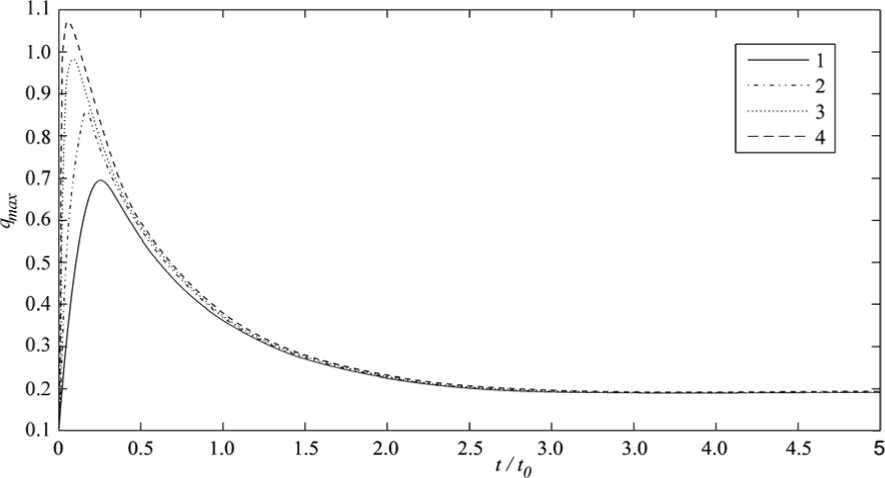
Рис. 5. Зависимость максимума давления от времени: 1 – ε = 0,04; 2 – ε = 0,02; 3 – ε = 0,01; 4 – ε = 0,005
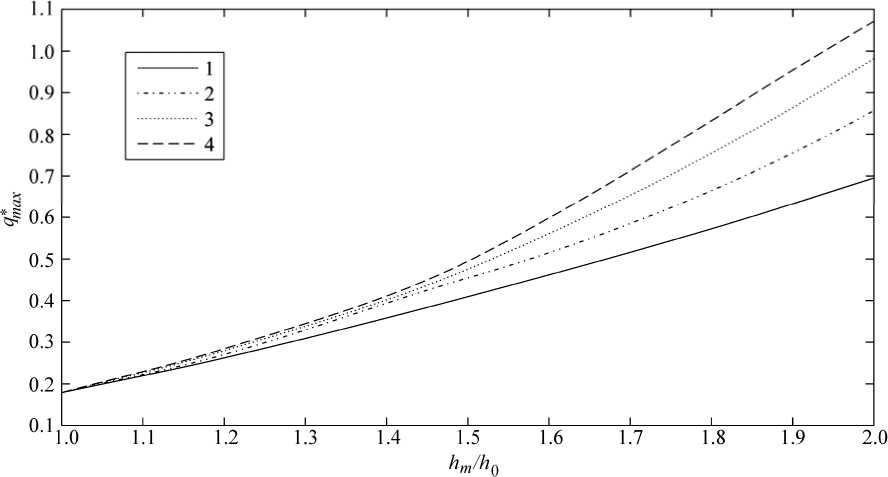
Рис. 6. Влияние начального условия на изменение пика давления для различных ε : 1 – ε = 0,04; 2 – ε = 0,02; 3 – ε = 0,01; 4 – ε = 0,005
Заключение. Построено асимптотическое аналитическое решение задачи нестационарного контактного взаимодействия ролика с твердой поверхностью при наличии смазочного слоя в зоне контакта. Показано, что процесс установления характеризуется двумя временными масштабами. Первый – определяет резкий рост максимума давления сразу после скачка нагрузки. Второй – отражает процесс плавной релаксации давления к стационарному значению, соответствующему возросшему значению нагрузки. Полученные результаты обосновывают важность учета нестационарных переходных процессов в узлах трения летательных аппаратов. Если при медленном (квазистационарном) возрастании нагрузки в 2 раза максимальное по слою давление испытывает примерно двукратное увеличе- ние, то в результате аналогичного по величине, но внезапного скачка нагрузки максимальное по слою давление во время переходного процесса кратковременно возрастает более чем на порядок. Такой значительный и резкий скачок давления в смазочном слое может критически отразиться на ресурсе всего узла трения.
Список литературы Нестационарные колебания ролика, контактирующего с твердой поверхностью, при наличии смазочного слоя
- Коднир Д. С. Контактная гидродинамика смазки деталей машин. М.: Машиностроение, 1976. 304 с.
- Галахов М. А., Усов П. П. Дифференциальные и интегральные уравнения математической модели теории трения. М.: Наука: Физматлит, 1990. 280 с.
- Терентьев В. Ф., Еркаев Н. В. Трибонадежность подшипниковых узлов в присутствии модифицированных смазочных композиций. Новосибирск: Наука, 2003. 142 с.
- Коднир Д. С. Контактная гидродинамика смазка деталей машин. М.: Машиностроение, 1976. 304 с.
- Александров В. М., Ромалис Б. Л. Контактные задачи в машиностроении. М.: Машиностроение, 1986. 176 с.
- Александров В. М., Чебаков М. И. Аналитические методы в контактных задачах теории упругости. М.: Физматлит, 2004. 301 с.
- Аргатов И. И. Асимптотические модели упругого контакта. СПб.: Наука, 2005. 447 с.
- Беспорточный А. И. Асимптотические режимы гидродинамического контакта жестких цилиндров, покрытых тонкими упругими слоями//Труды МФТИ. 2011. Т. 3, № 1. С. 28-34.
- Беспорточный А. И., Галахов М. А. Математическое моделирование в триботехнике. М.: МФТИ, 1991. 88 с.
- Галин Л. А. Контактные задачи теории упругости и вязкоупругости. М.: Физматлит, 1980. 304 с.
- Иванов В. А., Еркаев Н. В. Моделирование нестационарного контакта в подшипнике качения//Вестник СибГАУ. 2015. № 3 (16). С. 580-586.
- Галахов М. А., Гусятников П. Б., Новиков А. П. Математические модели контактной гидродинамики. М.: Физматлит, 1985. 296 с.
- Тихонов А. Н. Арсенин В. Я. Методы решения некорректных задач. М.: Наука, 1979. 288 с.
- Васильева А. Б., Бутузов В. Ф. Асимптотические методы в теории сингулярных возмущений. М.: Высш. шк., 1990. 208 с.
- Васильева А. Б., Бутузов В. Ф. Асимптотические разложения решений сингулярно возмущенных уравнений. М.: Наука, 1973. 272 с.


