Нестационарные одномерные динамические задачи разномодульной упругости с кусочно-линейной аппроксимацией краевых условий
Автор: Дудко О.В., Лаптева А.А., Рагозина В.Е.
Статья в выпуске: 4, 2019 года.
Бесплатный доступ
Объектом исследования является разномодульная упругая среда, подверженная динамическому деформированию. Разномодульность (зависимость связи «напряжения - деформации» от направления деформирования) является характерной особенностью множества природных и конструкционных материалов: горных пород, пористых и связных сыпучих сред, волокнистых и зернистых композитов, некоторых металлических сплавов и т.д. Перечисленные материалы проявляют свойство разномодульности уже на стадии упругого деформирования, что особенно необходимо учитывать при решении задач их ударной динамики. Для описания разномодульного поведения упругой среды в терминах малых деформаций в работе используется физически нелинейная модель В.П. Мясникова. Принятое предположение об одномерном характере деформации сводит нелинейную связь напряжений и малых деформаций к кусочно-линейным уравнениям. При динамической ударной деформации исходная нелинейность модели сосредотачивается в уравнениях, задающих скорость ударной волны, которая скачком переводит разномодульную среду из состояния растяжения к сжатию. В работе исследуются процессы возникновения, движения и возможных взаимодействий плоских одномерных волн деформации (включая ударные волны) в разномодульном упругом полупространстве. Граничные точки полупространства совершают одномерные движения по заданному нелинейному закону, соответствующему режиму «растяжение-сжатие». Нестационарное краевое условие задачи предлагается заменить на его кусочно-линейную аппроксимацию, что позволяет построить связанную последовательность аналитических решений с линейным краевым условием на каждом локальном временном интервале. Предложенный подход является основанием алгоритма численного решения краевой задачи с исходным нелинейным условием. Показано, что общее решение за ударной волной состоит из нескольких локальных слоев, число которых связано с количеством узлов кусочно-линейного разбиения краевого условия. В этих слоях деформация сжатия не только определяется соответствующей частью краевого условия, но и «хранит» информацию о предварительном растяжении, что следует считать важной особенностью динамики разномодульной среды.
Упругость, разномодульная среда, нестационарное деформирование, кусочно-линейная аппроксимация, одномерное движение, плоские волны, взаимодействие волн
Короткий адрес: https://sciup.org/146281967
IDR: 146281967 | УДК: 539.3:517.958 | DOI: 10.15593/perm.mech/2019.4.04
Текст научной статьи Нестационарные одномерные динамические задачи разномодульной упругости с кусочно-линейной аппроксимацией краевых условий
ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2019PNRPU MECHANICS BULLETIN
Известно, что большинство природных и конструкционных материалов обладают существенной нелинейностью связи между напряжениями и деформациями. Разномодульные среды занимают особое место в этом ряду, поскольку их нелинейность имеет практически сингулярный характер и проявляется уже на стадии упругого деформирования. В первую очередь это касается горных пород [1-5], всевозможных пористых и связных сыпучих сред [6-8], волокнистых и зернистых композитов [9-12], а также некоторых современных сплавов [13-16]. Распространенность и промышленная ценность таких материалов являются причиной активного экспериментального и теоретического изучения их физикомеханических свойств. К настоящему времени разработан целый ряд нелинейных математических моделей разномодульных сред (например, [17-23]), поскольку классических представлений линейной теории здесь оказывается недостаточно. Учет физической нелинейности разномодульного материала достигается в модельных соотношениях самыми разными способами: зависимостью упругих модулей от типа напряженно-деформированного состояния [21, 22, 24], постулированием упругого потенциала особой формы [17-20, 23], построением различных реологических схем [25-29] и т.д. В [30] на основе компиляции подходов [17, 18, 20, 24] модельные соотношения разномодульной упругой среды в простейшем случае ее одномерного движения записаны в форме кусочно-линейных функций напряжения от деформации. Замена гладкой нелинейной связи на ее кусочно-линейную аппроксимацию существенно упрощает процедуру решения ряда нестационарных краевых задач одномерной динамики разномодульной среды. Так, в [31] представлены обобщенные решения с одиночными плоскими одномерными волнами деформаций, возникающими в разномодульной среде [18] при различных гладких нелинейных краевых условиях; в [32] для этой же модели получено решение одномерной задачи о гармоническом нагружении границы полупространства с чередованием ударных волн и жестких слоев; в [33-35] рассмотрено движение одномерных плоских и сферических волн в кусочно-линейной разномодульной среде при кусочно-гладком изменении граничной нагрузки с растяжения на сжатие или наоборот. Однако до сих пор для разномодульных материалов не затрагивался вопрос о нестационарном взаимодействии нелинейных волновых фронтов друг с другом, поскольку даже кусочно-линейные модельные соотношения не позволяют в этом случае обойтись без привлече- ния специальных приближенных методов [36]. Данную проблему можно в некоторых частных случаях снять, если в дополнение к линеаризации модельных соотношений разномодульной среды выполнить кусочнолинейную аппроксимацию нестационарных краевых условий задачи. Продемонстрируем это в настоящей статье.
1. Определяющие соотношения
Запишем систему модельных уравнений динамики деформирования разномодульной упругой среды в прямоугольных декартовых координатах, считая, что процесс адиабатический, деформации малые и массовые силы отсутствуют:
_ д W р .
° ij, = Р Vi , ° = д--- , --- = 1 - uk, к ’ д eij Ро
-
2 e ij = u i, + u j , i , v i = i t i ,
X _2
E 1 e kk , E 2 ei k e ki .
Здесь ° у - компоненты тензора напряжений Коши; e ij -компоненты тензора малых деформаций; р 0 и р - начальная и текущая плотность среды; u i и v i -компоненты вектора перемещений и вектора скорости перемещений точек среды; латинским индексом после запятой обозначена частная производная функции по независимой пространственной переменной x^ , точкой -частная производная по времени t . Различное сопротивление материала растяжению и сжатию в системе (1) постулируем упругим потенциалом среды W [18, 20], где X , ц - параметры Ламе линейной среды, дополнительное слагаемое с константой v отвечает за проявление эффекта разномодульности при смене типа деформированного состояния. Многоточием обозначены невыписанные слагаемые неаналитичного при ey = 0 разложения [20] упругого потенциала в ряд по сферическим функциям, для которого в [20] дополнительно принято W (0) = 0 и показано существование пределов lim W ( e ij ) = 0, lim д W 1 6 e ij = 0. В случае
I e ij l ^ 0 I e ij l ^ 0
одномерного движения точек среды ( u 1 = u ( x , t ), u 2 = u 3 = 0, e = u , x ) упругий потенциал W в форме (1) приводит к кусочно-линейной зависимости ° ( e ):
° ( e ) = { X + 2 ц- 2 v- sign( e )} e , ° (0) = 0, (2)
где sign( e ) = e /1 e | при e * 0 . Аналогично обобщенной модели [20] второе равенство (2) обеспечивает сохранение непрерывности связи ° ( e ) в нуле. Используя (2), из системы (1) получаем уравнение движения
2 I a = 7Р- 1 (Х + 2ц + 2v), u , x < 0,
СИ , xx = U, с = ^ -------------- (3)
[ b = уР 1 (Х + 2ц-2v), u , x > 0.
В (3) характеристическая скорость с может принимать различные значения в зависимости от типа деформации: с = а в областях сжатия среды, с = b в областях растяжения (а > b при v> 0). Решение уравнения (3) в форме Даламбера u (x, t) = f (t - x/c) + g (t + x/c) (4)
с неизвестными функциями f ( £ ( x , t )), g ( n ( x , t )) определяется для каждой конкретной задачи с учетом заданных краевых и начальных условий.
Если в обобщенном решении уравнения движения (3) возникает одномерный фронт сильного разрыва x = D ( t ), то множество краевых условий задачи необходимо дополнить условиями совместности разрывов [37] и требованием непрерывности перемещений на поверхности D ( t ):
[°] = -р+ D '( t )[ v ], [ v ] = - D '( t )[ u , x ], [ u ] = 0. (5)
В (5) и далее разрывы функций на фронте D ( t ) обозначены как [ m ] = m + - m" , где m += m l , , „,
L J ’ ID (t )+0 ’ m~ = m\D(t)-0. Из условий (5) для модели (2) можно вычислить скорость сильного разрыва:
D'(t) = u +
X + 2 ц 2 v ■ sign( u ,- ) - 2 v ■ [sign( u , x )]—■■ [ u , x I.
/ + (6) р ,
которая оказывается зависимой от деформированного состояния ( u , + , u , - ) в малых окрестностях с обеих сторон от фронта D ( t ). Как будет показано далее, такая модельная особенность приводит к существенным отличиям динамики разномодульной среды от известных результатов линейной упругости даже в простейшем случае одномерных движений.
Для классификации возможных сильных разрывов D ( t ) в обобщенном решении уравнения (3) используем терминологию, аналогичную принятой в [38]. Если u , + * 0 и u,*u , - > 0, то в среде распространяется быстрый или медленный простой разрыв x = ^ ( t ); если u , + u , - = 0 при u , + * u , - , то такая волна - быстрый или медленный полусигнотон x = у ( t ) . Из (5), (6) следует, что простые разрывы и полусигнотоны в среде (2) движутся с характеристической скоростью c , равной а для быстрых фронтов у ± a ( t ), ^ ± a ( t ) и b для медленных Y ± b ( t ), ^ ± b ( t ) [31, 38] (знаками «+» и «-» у верхних индексов а ( b ) обозначим противоположные направления движения быстрых (медленных) фронтов;
далее знак «+» будем опускать). Ударной волной x = S ( 1 ) со скоростью S' ( 1 ) = G ( 1 ) будем называть такой сильный разрыв, у которого u,*u, x < 0 . Используя (5), (6), для модели (2), (3) можно показать, что b <| G ( 1 )|< a [31, 38].
Согласно приведенной классификации, простой разрыв £ ( 1 ) и ударная волна 2 ( 1 ) распространяются только по ненулевому предварительному полю деформации u , + * 0 . Ударная волна скачком меняет тип деформации с растяжения ( u , + > 0, с + = b ) на сжатие ( u , - < 0, с - = a ). Следует отметить, что ударный переход от сжатия к растяжению невозможен в силу неэволюционности такого разрыва [39]. Простой разрыв, в отличие от ударной волны, не изменяет тип деформированного состояния среды. Полусигнотон у ( 1 ) несет ударное граничное возмущение (растяжение или сжатие) в предварительно недеформированную область ( u , + = 0). Кроме того, в разномодульной среде (2) быстрый и медленный полусигнотоны могут двигаться парой, образуя между собой жесткий слой у b ( 1 ) < x < у a ( 1 ) при переходе предварительно сжатого материала в растянутое состояние [31, 32, 38].
Перечисленные свойства сильных разрывов в обобщенном решении уравнения движения (3) далее используем для анализа возможных волновых картин в задаче нестационарной одномерной динамики разномодульной среды.
2. Движение и взаимодействие плоских одномерных волн деформациив разномодульном упругом полупространстве
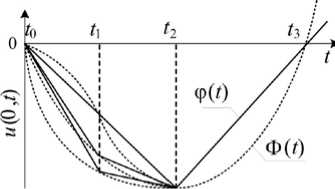
Рассмотрим задачу об одномерном динамическом деформировании разномодульного упругого полупространства под действием нестационарного граничного нагружения в режиме «растяжение-сжатие». Считаем, что изначально среда находилась в недеформированном состоянии: u 0 = 0 , e 0 = 0 , ст0 = 0. Пусть в момент 1 0 = 0 на границу x = 0 полупространства x > 0 начинает действовать нагрузка, вызывающая движение граничных точек по гладкому нелинейному закону u (0, 1 ) = Ф ( 1 ) (пунктирная линия на рис. 1): Ф ( t )| 1 0 < t < 1 3 < 0, ф ( t )| t > 1 3 > 0, ф ( 1 0 ) = ф ( 1 3 ) = 0, Ф '( 1 2) = 0, 1 0 < 1 2 < 1 3. Такое одномерное движение точек границы x = 0 приводит к растяжению среды при 1 0 < 1 < 1 2 и к сжатию при 1 > 1 2.
В [34,35] для описанного режима граничного воздействия показано, что в момент t2 в разномодульной среде (2) возникает ударная волна S(1), которая движется со скоростью G(1) > b за первичным медленным фронтом уb (t) и скачком переводит среду из растянутого состояния в сжатое. Однако временной интервал представленных в [34,35] решений не включает момент, когда ударная волна догонит идущий впереди нее медленный фронт растяжения. Здесь мы не будем накладывать таких ограничений, так как изучение взаимодействия волновых фронтов различного типа в разномодульной среде (2) является одной из основных целей нашего исследования.
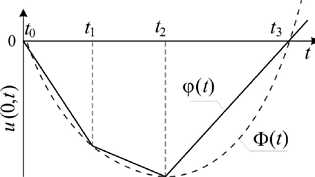
Рис. 1. Заданное перемещение граничных точек полупространства
Fig. 1. Displacement specified for boundary points of a half-space
Для заданной гладкой функции граничных перемещений u (0, 1 ) = Ф ( 1 ) можно построить ее непрерывное кусочно-линейное приближение:
y
1
(
t
),
1
0
<
t
...
. у. ( 1 ), t n - 1 < 1 ,
y. (1) = kit + pi, ti- < 1 < ti, i = 1,2,...,n, n > 2, k, = ф _ фi-1, p, = фi-1 - kt-1, ф, = ф(i,), y( tj) ‘ = yj+dtj) =Ф( tj), j = 1,2,..., n-1.
В (7) количество и расположение узловых точек t i функции ф ( 1 ) выбирается в зависимости от желаемой точности аппроксимации. Примем в (7) n = 3 и построим функцию ф ( t ) в форме трех линейных участков (сплошная линия на рис. 1):
ф ( 1 ) = •
y 1 ( t ) = k 1 1 + Р 1 , y 2( t ) = k 2 t + Р 2 , y 3( t ) = k 3 t + p 3 ,
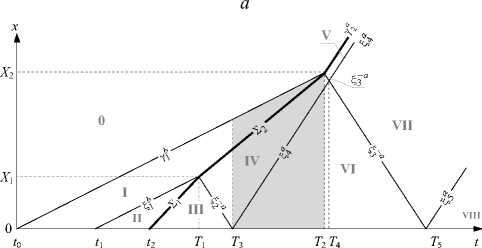
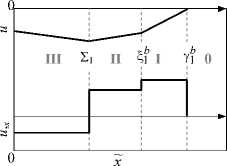
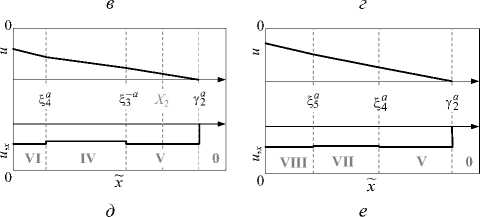
0 < 1<11, t1 < t Константы ki, pi в (8) вычисляются согласно (7). Три узловые точки функции ф(t) фиксируем при постановке задачи: 10= 0 и 13> 0 соответствуют нулям функции Ф( t), ф0=Ф( 10) = 0, ф3=Ф( 13) = 0; 12 -момент изменения граничной нагрузки с растяжения на сжатие (Ф'(12) = 0). Положение точки 11 может быть любым в интервале (0; 12). Таким образом, нестационарную начально-краевую задачу с гладкой функцией граничных перемещений u(0,1) = Ф( 1) разбиваем на несколько последовательных временных этапов, выбирая для каждого из них соответствующую часть кусочно-линейного краевого условия (8). Прогноз волновой картины на текущем этапе строим исходя из результатов предыдущего этапа. В дополнение к (8) в систему краевых условий каждого локального этапа включаем условия (5) на подвижных границах – фронтах сильных разрывов. Действуя по описанному алгоритму, получаем последовательность автомодельных решений, объединение которых составляет кусочно-гладкую аппроксимацию полей u(x,t) и u,x (x,t) во всей области деформирования на интервале t е [t0; t*]. Момент t* > t2, позже которого волновая картина уже не меняется при заданном формулой (8) движении граничной плоскости, является здесь точкой остановки вычислительной процедуры. Этап 1: нестационарное растяжение разномодульного полупространства при t е [0; t2). Согласно (8) движение точек границы x = 0 на интервалах времени t е [0; t1) и t е [t1; t2) определяется функциями у1 (t) и y2 (t) соответственно. Результатом такого граничного воздействия являются два медленных волновых фронта (рис. 2): полусигнотон yb (t) и простой разрыв Sb (t). б Рис. 2. Диаграммы сильных разрывов и областей гладкого решения: a - сценарий AB (T2< T3, b < G1 < G2< a); б - сценарий BA (T3 < T2, b < G2< G1 < a) Fig. 2. Diagrams for strong discontinuities and regions of a smooth solution: a - AB scenario (T2< T3, b < G1 < G2< a); b - BA scenario (T3 < T2, b < G2< G1 < a) Область 0 соответствует начальному (недеформиро-ванному) состоянию материала, в областях I и II среда подвергается растяжению (cI = cII = b). Полусигнотон Yb (t) (волна первичного растяжения) возникает в начальный момент 10 = 0 . Появление простого разрыва Sb (t) обусловловлено исключительно наличием излома функции ф(t) в точке t1. Здесь стоит отметить, что увеличение количества фронтов Sb (t) на этапе 1 за счет увеличения числа узловых точек ti е [0; 12) повышает точность аппроксимации всего решения, однако для наших целей достаточно одного простого разрыва Sb (t). С учетом краевого условия (8) на этапе 1 при t е [0; 12) решение в областях I и II (см. рис. 2) принимает вид и'(x,t) = A. + B.t + Cx, A = p. = 0, B, = k, C = -k / b, Sb (l )< x u" (x,‘) L<x Yb (t) = bt, Sb (t) = b(t - s). Этап 2: нестационарное сжатие разномодульного полупространства с момента t2и до первого взаимодействия разрывов различного типа. В момент t2 режим граничной нагрузки меняется с растягивающих усилий на сжимающие. Согласно (8) движение граничных точек теперь задано функцией ф(t) = у3 (t). В результате в момент t2 на границе x = 0 возникает ударная волна Z1(t) (см. рис. 2), которая движется со скоростью G1 (b < G1 < a) в предварительно растянутую область II, создавая за собой новую область сжатия III (cIII = a при 0 < x< 21(t)). Такая волновая картина существует в полупространстве до момента t = T1, когда ударная волна 21 (t) догонит медленный простой разрыв Sb (t) (см. рис. 2). Как и перемещение uIII(x,t), скорость G1 входит в число неизвестных функций задачи. Eсли условие на границе x=0 задано в форме гладкого нелинейного закона и(0,t) = Ф(t), то G1 в (5), (6) будет зависеть, кроме t , еще и от неизвестного скачка [и,x ]|z, (t) = (и,+ — и,- )|2 (t). В таком случае решение даже простой одномерной краевой задачи можно получить только численно или с привлечением специальных приближенных аналитических методов [36]. Замена нелинейной функции Ф(t) ее кусочно-линейной аппроксимацией (8) позволяет существенно упростить процедуру решения, так как перемещение граничных точек по линейному закону ф(t)|(>( = у3(t) инициирует ударную волну 21 (t), которая движется по предварительному полю и,x = const > 0 с постоянной скоростью: 2 22 k /b G, = a - (a - b )------------= const, b < G, < a, u Ш(x,t) |0 B3= k2(1 - G1 / b) + RG1 /a, C3= -R / a. Этап 3: эволюция ударной волны X, (t) в результате ее взаимодействия с медленным простым разрывом Sb (t). Область растяжения II перестает существовать при t = T1 > t1, когда ударная волна £1 (t) догоняет простой разрыв Sb (t) (см. рис. 2). Положение, которое в момент T занимают волны £1 (t) и Sb (t), определяется координатой X1 = Е,(T1) = Sb (T). В результате такого попутного столкновения £1 (t) и Sb (t) транформи-руются в два новых фронта, расходящихся от плоскости x = X 1 (см. рис. 2): быстрый простой разрыв S- a (t) и ударную волну £2 (t) со скоростью G2 ^ G1. Решение в новой области сжатия IV (cIV = a ) имеет вид u IV( x, t )| = A + B. (t - T) + Cx, v ’ ' k-a (t) S-a (t) = X1 - a (t - TO, £2 ( t) = X1 + G2( t - T), T = G1 t2 -btx 1 G1 - b ’ X1 = ^( T) = Sb (T) = bG1(12 -11) G1 - b A4 = k1 t1 - p1 -C4 X1, B4 = bG2( k3+ R) + ak1( b - G2) b (a + G2) C4 = k1( b - G2) - b (k3+ R) b (a + G2) В (12) скорость G2 ударной волны £2(t) вычисляется из (5) с учетом (8), (9), (11) по формуле G2 k1( a2- b2) k1( a + b) - b (k3+ R) = const ^ G1, b< G2< a. Этап 4: эволюция ударной волны X2 (t) в процессе нарастающего сжатия на границе полупространства. Система разрывов {S-a, £2, yb} существует до момента наступления одного из событий: A = {£2(T2) = yb (T2) = X2} - попутное столкновение ударной волны £2(t) с медленным полусигнотоном Yb (t) в момент t = T2 (X2= X 1 + G2(T2- T) = bT2); B = {S-a (T3) = 0 } - отражение быстрого простого разрыва S-a (t) от границы x = 0 в момент t = T3. Таким образом, дальнейшее решение может развиваться по различным сценариям: AB (T2 < T3) или BA (T2 > T3). Случай T2 = T3 не рассматриваем ввиду малой вероятности одновременного наступления событий A и B. Опуская подробности дальнейших вычислений, представим решения для каждого из указанных вариантов. На рис. 2, a показана диаграмма сильных разрывов для случая AB (T2 < T3), на рис. 2, б - для случая BA (T2 > T3). Области, где волновые картины различаются, отмечены штриховкой. При T2 < t < T3 (см. рис. 2, a) волновой пакет состоит только из быстрых разрывов {S-a, S-a, Ya}, разделенных областями сжатия III, IV и V (c111 = cIV = cV = a ), причем полусигнотон у a (t) и простой разрыв S-a (t) есть результат события A. В случае T3 < t < T2 (рис. 2b) волновая картина включает попутные разрывы {S4, X2’ Yb}, движущиеся с различными скоростями, и области с разными типами деформации: в IV и VI - сжатие (cIV = cVI = a), в I - растяжение (cI = b). Таким образом, ударная волна £2(t) может как закончить свое существание в самом начале этапа 4 в момент t = T2 < T3 вследствие ее трансформации в быстрые разрывы у a (t) и S- a (t) (вариант AB), так и продолжать участвовать в формировании поля деформации в областях сжатия IV, VI на всем протяжении этапа 4 вплоть до момента t = T2 > T3 (вариант ВА). Это приводит к двум различным наборам краевых условий (5) на сильных разрывах для случаев AB и BA. С учетом данного факта перемещение u(x,t) в областях V и VI вычисляется в виде u V(x, t )| E- am T2 = T1 + bt1/(G2 - b), uVI(x,t)|0< T3= T + X J a, S-a (t) = X2 - a (t - T2), у a (t) = X2 + a (t - T2), (14) S4 (t) = a (t - T3), A5 = 0.5X2(B4/a -C4), B5= 0.5(B4-aC4), C5 = 0.5(C4 -B4 /a), A6 = p 3 + k3 T3, B6 = k3, C6 = (B4 -k3)/a + C4. Константы B4, C4 в (14) известны из решения (12), (13) предыдущего этапа 3. Этап 5: продолжение сжатия на границе полупространства при t > T3 или t > T2 в зависимости от сценария предыдущего этапа (AB или BA). На данном этапе, начало которого совпадает с моментом t = T3 (вариант AB, рис. 2, a) или t = T2 (вариант BA, рис. 2, б), движение точек граничной плоскости по-прежнему определяется согласно (8) функцией ф(t) = y3 (t). В любой момент этапа 5 волновая картина состоит из трех быстрых разрывов (попутных или разнонаправленных, рис. 2), тип деформации во всех актуальных областях гладкого решения соответствует сжатию. Передним фронтом сжатия является быстрый полусигнотон у ° (t), который движется в недеформированную область 0. Помимо у ° (t), в формировании полей u (x, t) и u, x в областях V–VIII участвуют быстрые простые разрывы ^з a (t), ^4 (t), ^ (t). Неизменность типа деформации на протяжении всего этапа 5 приводит к постоянству характеристической скорости c всюду между передним фронтом у ° (t) и границей x = 0 (cV = cVI = cVII = = cVIII = a), а также к сохранению характера сильных разрывов ^±° (t) при их взаимодействии друг с другом (при t = Т4) и с границей полупространства (при t = Т5). Это позволяет легко получить решение задачи в областях VII, VIII: uVII(x, t) = A + Bn (t - T) + Cx, V ’ 71 ^a (t) u VIII (x, t )| „ = A + B8 (t - T) + Cx, o< x <^ (t) 8v 578 T4 = 0.5( T2 (a + b)/ a + T3), T5 = 2T4 -T3, ^ = a(t-T5), A = A + B5(T4 -T2) + a(T4 -T3)(C5 -C7),(15) B7 = 0.5(B4+ B5 - a (C6 - C5)), C7= 0.5(B5- B6 + a (C5+ C6)) / a, A = A7 + B7( T5 - T4), B8 = k3, C8 = (B7-k3)/a + C7. Как показано на рис. 2, в обоих случаях AB и BA при t = T5 возникает волновой пакет из попутных быстрых разрывов {^^, ^4, Ya}, который уже не изменяется с течением времени, если граничные точки продолжают двигаться по закону u (0, t) = y3(t). Таким образом, процедуру решения описанной задачи можно остановить в любой момент t* > Т5, например, руководствуясь оценкой масштаба реального граничного перемещения u(0,t*) , достигнутого к этому моменту времени.
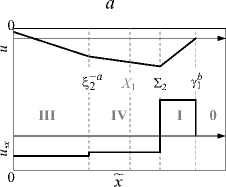
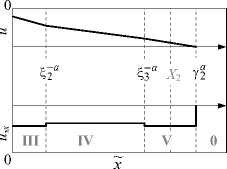
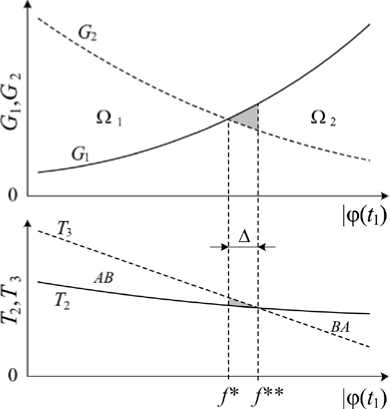
3. Анализ решения На рис. 3 схематически изображена последовательность моментальных кусочно-линейных диаграмм перемещения u(x,r) и деформации u,x (X,т) , соответствующих полученным решениям (9) – (15) при возникновении случая AB (Т2< Т3). На каждой диаграмме момент т принадлежит одному из описанных выше этапов деформирования, условная пространственная координата x имеет свой нормирующий множитель, характерный для выбранного интервала времени: (a) t1<т<12, x = x/(bт); (б) 12<т<Т1, x = x/(G1т) ; (в) T< т < T2, x = x / (G2т); (г) T2< т < T3, x = x / (a т); (д) T3< т < T4, x = x / (a т); (е) т > T5, x = x / (a т). Рис. 3. Результаты поэтапного решения краевой задачи (сценарий AB) Fig. 3. Results of the stepwise solution for the boundary value problem (AB scenario) Несомненно, рис. 3 не отражает всех возможностей развития системы разрывов и полей u , u,x в рассмотренной задаче. Так, на рис. 2 показано, что кусочнолинейная геометрия ударного фронта 21 + S2, которая определяется значениями скоростей G1 и G2 , может изменяться в зависимости от положения узловой точки t1 функции ф(t) в (8). Устремляя данную точку к началу процесса растяжения (моменту 10= 0), мы получаем вогнутую форму фронта 21 +22, так как b< G1< G2< a (см. рис. 2, a); если точка t1 расположена ближе к моменту 12, то разрыв 21 + 22 принимает выпуклую форму при b< G2< G1 < a (см. рис. 2, б). Аналогичного эффекта можно добиться при фиксированном положении узла t1 путем изменения значения ф(t1), т.е. фактически варьируя кривизну функции u (0, t) = Ф( t) на интервале растяжения t е [0;12] (рис. 4). Полученные с учетом (8), (10), (12)–(14) зависимости скоростей G1 , G2 и моментов T2 , T3 от величины | ф(tj)| схематически показаны на рис. 5, где f* = Ф(t1) | G = g2, f ** = Ф(t1) | t2=t3 ; G1 < G2 в области Q3 при | Ф(t1)|< f *, G1 > G2 в Q2 при | ф(t1)|>f *; T2< T, при | ф(t1) |< f ** (сценарий АВ), T2> Т3 при | ф(О l>f ** (сценарий BA). Отметим, что значения f * и f ** в общем случае не совпадают, т.е. существует узкий диапазон A=|f **- f *|~10-3 м, где при G1> G2 волновая картина на этапе 4 (нарастающее сжатие) может развиваться по сценарию BA при T2 > T3 (заштрихованные области на рис. 5). Рис. 4. Функция граничного перемещения с вариацией кривизны на стадии растяжения Fig. 4. Boundary displacement function with curvature variation at the stretching stage Рис. 5. Зависимости параметров решения от значения | ф(г1)| Fig. 5. Dependencies of solution parameters on the value | ф(?1)| Заключение Итак, в статье показано, что кусочно-линейная аппроксимация нелинейных краевых условий динамической задачи позволяет описать процесс возникновения, движения и взаимодействия плоских одномерных волн деформаций в разномодульной упругой среде, не обращаясь к специальным методам типа метода возмущений и др. Полученное с помощью такого подхода кусочно-линейное решение моделирует нелинейный эффект, характерный для динамики деформирования нелинейно-упругих материалов и не описываемый в рамках линейной упругости – возникновение ударной волны сжатия со скоростью, зависящей от динамического поля деформаций по обе стороны от волнового фронта. Данный подход можно использовать для решения нестационарных краевых задач упругой динамики нелинейных и разнопрочных сред с более сложными граничными условиями, чем представленное здесь (например, режимы циклической нагрузки-разгрузки или вибрации), при этом точность решения может быть улучшена путем добавления дополнительных узловых точек аппроксимирующей кусочно-линейной граничной функции. Также результаты работы могут послужить теоретическим дополнением для экспериментальных исследований нелинейного поведения реальных природных и конструкционных материалов под действием высокоскоростных динамических нагрузок. Работа выполнена при частичной поддержке Программы «Приоритетные научные исследования в интересах комплексного развития Дальневосточного отделения РАН» (проект 18-5-002). Acknowledgments This work was supported in part by the Program “Priority Scientific Research for the Comprehensive Development of the Far Eastern Branch of the Russian Academy of Sciences” (project 18-5-002).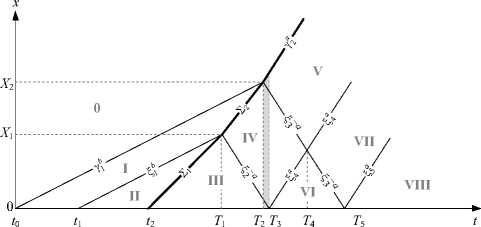
b(t) = A2 + B(‘ — t1) + C2x, A2 = p2, B2 = k2, C2 = -k2 7 b,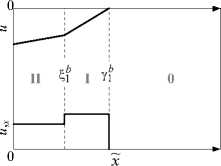
Список литературы Нестационарные одномерные динамические задачи разномодульной упругости с кусочно-линейной аппроксимацией краевых условий
- Капустянский С.М. Анизотропия геоматериалов // Итоги науки и техники. Механика деформируемого твердого тела. - 1987. - Т. 18. - С. 53-113.
- Ставрогин А.Н., Протосеня А.Г. Прочность горных пород и устойчивость выработок на больших глубинах. - М.: Недра, 1985. - 271 с.
- Experimental investigation of the anisotropic mechanical behavior of phyllite under triaxial compression / Guowen Xu, Chuan He, Ang Su, Ziquan Chen // International Journal of Rock Mechanics and Mining Sciences. - 2018. - Vol. 104. - Р. 100-112. DOI: 10.1016/j.ijrmms.2018.02.017
- Динамическое деформирование мягких грунтовых сред: экспериментальные исследования и математическое моделирование / В.В. Баландин [и др.] // МТТ. - 2015. - № 3. - С. 69-77.
- Баклашов И.В., Картозия Б.А. Механика горных пород. - М.: Недра, 1975. - 271 с.


