Нестационарные процессы в гиперзвуковом пограничном слое

Развитие возмущений представляет собой часть проблемы гидродинамической устойчивости. Анализ процессов передачи возмущений в пограничном слое позволяет исследовать устойчивость к длинноволновым возмущениям и корректно постановить задачи в условиях сильного вязко-невязкого взаимодействия.

При анализе системы уравнений пограничного слоя в [1, 2] показано, что характеристики представляют собой линии, перпендикулярные обтекаемой поверхности. На основе анализа характеристик и субхарактеристик была сформулирована постановка задачи для нестационарного двумерного пограничного слоя.

В данной статье рассмотрены нестационарные процессы в гиперзвуковом пограничном слое в условиях сильного вязко-невязкого взаимодействия. Из-за взаимодействия распределение давления заранее неизвестно и оно должно определяться в процессе решения задачи. В этом случае существует дополнительный механизм передачи возмущений, связанный с распространением волн давления. Поскольку в пограничном слое существует область дозвукового течения вблизи поверхности обтекаемого тела, эффект передачи возмущений вверх по потоку имеет место.

Исследование процессов распространения возмущений в пограничных слоях в условиях сильного гиперзвукового вязко-невязкого взаимодействия [4] позволило определить субхарактеристические поверхности, отделяющие области докритического (в среднем дозвукового) течения от закритического (в среднем сверхзвукового). В [5] было дано определение

«Московский физико-технический институт (национальный исследовательский университет)», 2019

докритического и закритического течений. Докритическими называются области, где возмущения могут распространятвся на расстояния, значительно превышающие толщины пограничного слоя, а закритическими - на расстояния, сравнимые с толщиной пограничного слоя.

В работах [6-8] рассмотрены нестационарные сверхзвуковые течения. В данной работе рассмотрены нестационарные процессы распространения возмущений в гиперзвуковом пограничном слое при условиях сильного взаимодействия. Такой случай имеет место, когда параметр взаимодействия [9] существенно больше 1 [3].

2.    Постановка задачи

Рассмотрено обтекание плоской поверхности (в том числе пластины и клина), расположенной под нулевым углом атаки, гиперзвуковым потоком вязкого газа в условиях сильного вязко-невязкого взаимодействия [9]:

М ^ ^ ж , М ^ т ^ то ,

где М_го - число Маха на бесконечности, т - безразмерная толщина пограничного слоя.

Вводятся следующие обозначения для координат, отсчитываемых вдоль поверхности пластины и по нормали к ней, времени, компонентов вектора скорости, плотности, давления, полной энтальпии, коэффициента вязкости: lx, ly, lt/uro, urou, urov, prop, prourop, иГО,Н/2, prop соответственно. Параметр l - некоторая характерная длина, т = (prourol/po), где индекс то относится к размерным параметрам невозмущенного набегающего потока; po - величина динамического коэффициента вязко сти, определенного при температуре торможения. Несмотря на то, что в гиперзвуковых потоках эффекты реального газа играют существенную роль, в данной работе пренебрегаем этими эффектами, поскольку их учет в общем не меняет соотношений, полученных ниже. Предполагается, что число Рейнольдса велико, но не превосходит критического значения, так что сохраняется ламинарный режим течения. Кроме того, при увеличении числа Маха также возрастает число Рейнольдса перехода.

Согласно теории сильного взаимодействия [9] можно разделить возмущенную область течения на две подобласти: I - ударный слой и II - пограничный слой.

В подобласти I функции течения и координат представлены в следующем виде:

(^x,y^,t) = ^(x i ^,Ty i ^,t i ⁾ ,

(и, v) = (1 + ...,TV 1 + ...) , (р, p, H ) = (т²p i + ..., p i + ..., H i + ...) .

Подставляя вышеуказанные разложения в систему уравнений Навье-Стокса, получим следующую систему уравнений, описывающую возмущенное невязкое течение в ударном слое:

^дР 1 + Әр і + dp i ^v i = 0 dt 1    9x 1     dy 1

dv 1    dv 1       dv 1    1 dp i

9ti + 9xi + V1 dyi + pi dyi dx (pi)

,    9 pPi\

^{+ Vi} dy i \pV

= 0

с граничными условиями на ударной волне yi = 9i (xi,ti) ,pi

7 + 1

7 — ¹,

P i =

⁽7 ^{+ 1) v}2 „      ?

, v

(to + to)

У 9xi 9t1 /

и на внешней границе пограничного слоя

У і = 5 1 (x i ,t i ) , щ =

2 д5 і + дф

7 +1 дх і    дһ ’

Для дальнейшего анализа использовалась формула касательного клина в нестационарном случае для установки связи между толщиной пограничного слоя и индуцированным возмущением давления:

7 ^{+ 1} 2 Р і = ""2"” ^і’

Для подобласти II функции течения и координат представлены в следующем виде:

(ж,у,і) = ДіщуіДД,

(n, г) = (« 2 + ...,ТГ 2 + •••) ,

^{( р}, ^р, ^Н ) = (^т 2 ^р 2 ⁺ ..’1 ^т 2 ^р 2 ⁺ •••’ ^Н 2 ⁺ ...) .

Подставляя последние разложения в систему уравнений Навье-Стокса, учитывая предельный переход (1), получим следующую систему уравнений нестационарного пограничного слоя:

XЭи эи_эғэи   ғ ди 7-1 _{п =} р^

Х дТ +   иэх дХ дҮ    4 дҮ +р 47 ^ С0 дҮ2 ’"

хд^^ X (т tG. _ GG А .IG- _у 7 - 1 _пдР . р_ д^и

• Х дТ + и дХ дХ дҮ 4 дҮ 7Р ^дТ + С0 дҮ2 ’°

∞ дҮ = °,S = -1 + -рдх’ Д = / ^4Ү’

Р = ^ (£ + х ( ^ + £)Р = G-и2,с где

I (7 - 1А - і / 4 f^m „ , .     3 / 4 д             дҒ

^Ү ДУадФ Л ^{Rdy v} ’ ^5і = ^ і ^Л;' =^и = аҮ’

Х = ц;Т = * і ;Р 2 = Т.-^Р ; Р 2 = T.^{-l f 2}R;C₀ = Р (0,Т); G = Н 2 ;

граничные условия и = Ғ = 0,G = gw ,Ү = 0,

U = 1,G = 1,Ү = то,

Р (Х = 1,Т) = Р (Т ).

Для определения единственного решения необходимо задать дополнительное условие на некоторой линии ниже по течению от передней кромки, например донное давление на задней кромке [3]. Появление дополнительного условия связано с возможным распространением возмущений вверх по потоку и их влиянием на течение в пограничном слое.

3.    Анализ субхарактеристик

Рассмотрены характеристические (субхарактеристические) поверхности П(Х,Т), связанные с функцией Р(Х,Т ), которая заранее не известна и должна определяться в процессе решения. После введения новых переменных Х,Ү,Т ^ П(Х,Т),Ү,Т краевая задача

(2-5) принимает вид

ди дИ идИ дИ дТ + иах)	ди дҒ д И дҮ д И дХ	. дР дИ + А1 дИ дХ = В" ’	(6)
дС / д И    дИ X	дС дҒ д И	дРдИ
дИ дТ + идх)	дҮ д И дХ	+ А 2 дИ дТ = В д ’	(7)
Р_ у + 1 (хд л Р = 2 Дах	/ дИ дИ Х дХ + дТ/	зл лалх2 + ^+Хағ) ’	(8)
А. = <К	- 1)С А = (7 — 1)С .		(9)
2уР '		7Р

Используя определение толщины вытеснения пограничного слоя, производную в правой части выражений (8-9) можно писать следующим образом:

дЛ_ Г^ дИ У :

-

2уР ²

“ ^д> д И

-

∞ р ди Z 9dҮУ

Для нахождения производной дИ преобразуем систему уравнений (6-7) к уравнению для функции дҒ дИ

= дИ дХ’

Из (6) получим уравнение

9D    ЭА о       у - 1 ЭР

Ао дҮ +D дҮ + 1Q 2^Р дИ

™ л„ = 8^ + и^,вү =

⁰ дТ дХ ¹

Уравнение (10) имеет решение

D = -В1А0^Д1 ій /У J2” + Ао /^ В4Ү’ 27Р дИ 0 А00 которое проводит к следующим выражениям для производных:

ди дИ

=  D^

А о    дҮ

-

. дРд и

^А1 д И дХ ^{+ и}у ’

дС дИ

=

А о    дҮ

-

. дРд И

^А 2 дИ дТ ^{+ Вд}) ’

Окончательно получим выражение для производной индуцированного давления в направлении, перпендикулярном к субхарактеристической поверхности:

дР дИ

^рвр _N 7 — ¹ дИ \ г дИ ^Л 2 (дх) ^{1 1 І 0} ’

^ дХ

І 0 = Г\с -и ²Ж.Ь

∞

■і= L

(G - U 2 ) 2

д И    д И

( дТ ^{+ и}дх)

2 dY.

После введения скорости перемещения субхарактеристической поверхности

_  1 д П д П

° = - В І д)Хд)Т'

Тогда выражение для N в (11-12) имеет вид

N =

7 - 1

∞

f - U222 dY — [~ ( G - U ² ) dY. ⁽° ^{+ U} Г      00

Субхарактеристическая поверхность П(Х, Т ) определяется условием N = 0. Последнее уравнение определяет среднюю скорость распространения возмущений вверх по потоку, если известны профиль скорости и энтальпии. Уравнение N = 0 представляет собой модификационный интеграл Пирсона [10].

4.    Метод решения задачи

Для решения задачи выбрана разностная схема для равномерной сетки, построенной на прямоугольной области 0 <  Х < 1, 0 <  Y < Уф = 7.

Задача решена маршевым методом слева направо по каждому слою при фиксированном Х.

Выбрана разностная схема второго порядка точности для дискретизации по Х [11].

Выбрана неявная трехточечная разностная компактная схема шестого порядка точности (three-point sixth-order combined compact 8сһете)для дискретизации по Y (построены матрицы дифференцирования первого и второго порядка Dly, D2y) [14,15].

Выбрана схема Кранка-Николсона второго порядка точности для дискретизации по времени.

Интеграл для толщины вытеснения пограничного слоя вычислен методом интегрирования шестого порядка точности (этот метод представляет собой следствие метода Симпсона четвертого порядка точности и экстраполяции Ричардсона).

Заданы функция /(ж) и 5 точек выборки ж₁, ж₂, жз, ж₄, ж5 с приращением Һ, тогда из формулы Симпсона получим:

Г ^ж 5

A o =    / (ж^ж,

J ^ 1

A h = ^Һ/(ж 1 ) ⁺ ^/^(ж 2 ) ^{+ Һ/(ж} 3 ) ^{+ Һ/(ж} 3 ) ⁺ ^/^(ж 4 ) ^{+ Һ/(ж} 5 ) , 3          3          3         3          3          3

^A 2 h = ² Q^/(ж 1 ) ⁺ у ^{/ (ж} 3 ) ⁺ 3f ^(ж 5 )) .

Используя экстраполяцию Ричардсона, получим метод интегрирования шестого поряд ка точности:

^A 0 = ^Ah ⁺ — ^{( A}h ^{- A}2h) = ^аһ^аһ ^— ү^Аііп 15               15      15

A o = ^ (7 / ( ж і ) + 32 / ( ж 2 ) + 12 / ( ж з ) + 32 / ( ж 4 ) + 7 / ( ж 5 )) .

Это так называемый метод Буля [16], для метода Буля погрешность интегрирования составляет лишь — 945 Һ 7 /⁽⁶⁾ ( с ) = — ( ж5 — ж^^у Һ⁶/⁽⁶⁾ ( с ) ,ж₁< с < ж5.

Из-за вязко-невязкого взаимодействия распределение давления заранее неизвестно, в данной статье мы знаем значение давления только при Х = 0 и Х = 1. Предложен итерационный метод [11, 12, 13] для определения распределения давления. На каждом шаге итерационной процедуры вводится функция невязки, представляющая собой разность между заданным и полученным в процессе решения задачи распределениями давления. Эта функция представляет собой решение обыкновенного дифференциального уравнения второго порядка относительно давлению.

Пусть в начале n-й итерации задано распределение давления р^(п)(ж) на равномерной по ж сетке в расчетной области [0, 1], удовлетворяющее граничному условию р^(п)(0) = Ро,р^(п)(1) = Р1. Тогда система уравнений (2-5) решается численно с релаксационным методом.

Рассчитанные переменные U (ж, у), (Дж, у) позволяют определить толщину вытеснения р ^ ^п ( (ж) с помощью (4), таким образом вычислить полученное распределение давления с помощью (5). Новое распределение давления определяется следующим образом:

р(«+1)(ж) = ^(ж) + Ар(п)(ж), где функция поправки Ар(п)(ж) представляет собой решение обыкновенного дифференциального уравнения второго порядка с граничными условиями. В отличие от итерационного метода, предложенного в [11], в данной работе вводится еще коэффициент «1, что позволяет ускорять итерационную процедуру:

^"АрЖ?Ж) + «1 аАрсһ)(Ж) — «АрН(ж) = « (//" -р^) , Ар(п)(ж = 0;1) = 0, где «, «1 - некоторые положительные константы.

Итерационный процесс продолжается до тех пор, пока функции не совпадут с заданной точностью на всем расчетном интервале. Для обеспечения устойчивости итерационного процесса численные эксперименты показывают, что значение коэффициентов «, /3 должно лежать в следующих интервалах 0.01 < « < 0.5, -30 < «1 < -20. Итерационный процесс закончится, если удовлетворяются критерии для абсолютной разности р(п) — р^ < 5.10-5

р(п) — р(п) или для относительной разности ---— р\п)

< 1.10 4. Требуются 150-300 итераций для достижения этого критерия сходимости на каждом шаге по времени.

Чтобы доказать рассуждение о том, что Ар(п)(ж) ^ 0,р(п+1)(ж) — р(п)(ж) ^ 0 при р(п) (ж) — р^п)(ж) ^ 0, рассмотрим однородную задачу

^^.J (ж' + «1 ^^^ — «АрН(ж) = 0, Ар(и) (ж = 0;1) = 0,

Ар(п)(ж) = СД71* + СД7^, 71,2 = —«1 ± ^«2 + 4«, Ар(п)(ж = 0;1) = 0 ^ СД0 + Де0 = 0; СД71 + СД72 = 0, ^ С1 = 0; С = 0 ^ Ар(п) (ж) = 0, Уж.

В этом случае обыкновенное дифференциальное уравнение второго порядка имеет только тривиальное решение.

5.    Результаты

Исследовано влияние дискретизаций по пространству и времени. Численные эксперименты показали, что шаги дискретизации по пространству и времени dX = 0.025, УУ = 0.25, dT = 0.01 обеспечивают необходимую точность решения задачи. Для дальнейших расчетов выбраны эти шаги дискретизации.

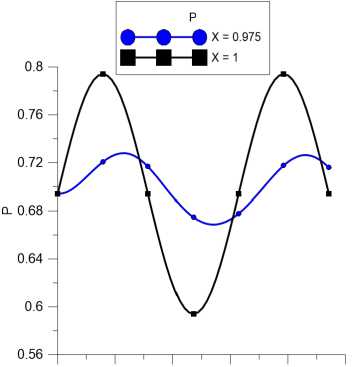
Дальше рассмотрен случай, когда донное давление меняется по синусоидальному закону с частотой / = ш/(2тт) = 0.5 и амплитудой атр = 0.1, Ру₌₁ = Ру=о + атр * 8Іп(2тт/Т).

Наблюдался сдвиг фаз распространения возмущений давления вверх по потоку из-за конечности скорости подачи возмущений вверх по потоку. Мы можем определить скорость распространения возмущений с помощью (13), если известны профиль скорости и энтальпии. Из-за конечности скорости подачи возмущений через некоторое время область, находящаяся вверх по потоку от задней кромки, получает информацию о течении на задней кромке. Был обнаружен эффект «замораживания» течения в областях, находящихся вверх по потоку, когда информация о течении на задней кромке пока не доходит до этих областей.

Из распределения давления и трения на пластине при разных фазах донного давления обнаружено явление того, что при увеличении давления трение уменьшается и, наоборот, при уменьшении давления трение увеличивается.

О 2       4       6       8       10

Рис. 1. Изменение возмущений давления при X = 1 и X = 0.975

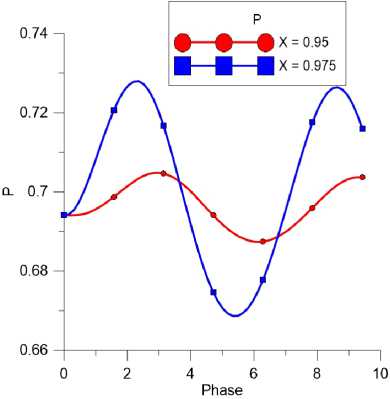
Рис. 2. Изменение возмущений давления при X = 0.975 и X = 0.95

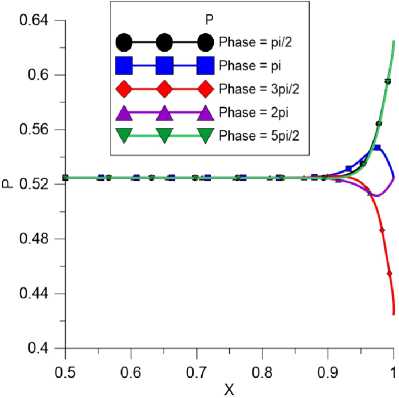
Рис. 3. Распределение давления при разных фазах донного давления

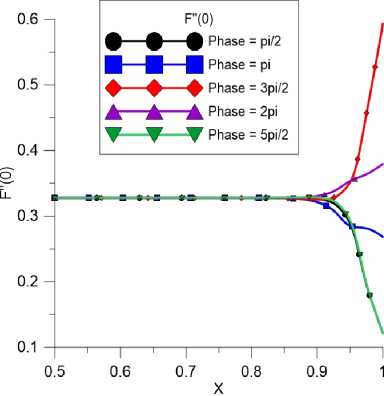
Рис. 4. Распределение трения на пластине при разных фазах донного давления

6.    Заключение

Получены следующие выводы.

• 1.    Обнаружен сдвиг фаз распространения возмущений вверх по потоку из-за конечности скорости распространения возмущений вверх по потоку. Обнаружен эффект «замораживания» течения области, находящейся вверх по потоку, в начальный момент времени.

• 2.    Наблюдалось явление того, что распределение давления оказывается в противофазе с распределением трения на поверхности пластины.