Нестандартная логика научных базисов образовательных процессов в сквозных информационных технологиях и когнитивных вычислениях. Ч. 1: проблема Бэкона, аналитика больших данных и теория интеллектуальных моделей познания физических процессов

NONSTANDARD LOGIC OF EDUCATION BACKGROUND IN END-TO-END

INFORMATION TECHNOLOGIES AND COGNITIVE COMPUTING.

PT. 1: BACON’S PROBLEM, BIG DATA ANALYTIC AND INTELLIGENT MODEL THEORY OF COGNITION PHYSICAL PROCESSES

Bagdasaryn Nadeshda1, Korenkov Vladimir2, Reshetnikov Pavel3, Tyatyushkina Olga4, Ulyanov Sergey5

• ¹Doctor of Philosophy Science, professor;

Bauman Moscow State Technical University;

Dubna State University;

Faculty of Social and Human Sciences;

141980, Moscow reg., Dubna, Universitetskaya str., 19;

• ²Doctor of Technical Science, professor;

Deputy Director of the Laboratory;

Joint institute for nuclear researches, Laboratory of Information Technologies;

141980, Moscow reg., Dubna, Joliot-Curie, 6;

• ³Student;

Dubna State University,

Institute of the system analysis and management;

141980, Dubna, Moscow reg., Universitetskaya str., 19;

• ⁴Ph D, Аssociate professor;

Dubna State University,

Institute of the system analysis and management;

141980, Dubna, Moscow reg., Universitetskaya str., 19;

• ⁵Doctor of Science in Physics and Mathematics, professor;

• 2.    1. Введение: Основы сквозных интеллектуальных информационных технологий для цифровой экономики и проблема познания Бэкона

Dubna State University,

Institute of system analysis and management;

141980, Dubna, Moscow reg., Universitetskaya str., 19;

Компьютерные технологии составляют базис «информатики» и относятся к классу основных приоритетных « сквозных информационных технологий ( ИТ )» для цифровой экономики². Однако перевод с английского « Computer Science » на русский язык как « Информатика » недостаточно точно отражает вложенное смысловое содержание в английский термин и приводит в ряде случаев к недопониманию целей и назначения данной науки, особенно при формировании образовательных процессов и переподготовке кадров. Во многих (отечественных и зарубежных) работах информатика (и как наука об эффективных алгоритмах и сложности вычислений в широком смысле, и как прикладной программно-аппаратный инструментарий с соответствующей сервисной поддержкой) отождествляется с понятием « Computer Science». Практически «информатика» рассматривается в основном как целевое назначение информационной технологии, применяемой в технической системе сбора, обработки и передачи данных с последующей коммерциализацией разработанного продукта.

Однако одним из важных социотехнических аспектов обсуждаемой проблемы разработки когнитивных интеллектуальных ИТ является совершенствование структур ИТ, влияющих на основы самоорганизации психических и когнитивных процессов, которые отвечают за способность поддерживать личностную целостность и идентичность [1, 2].

Каждый следующий уровень технологической сложности (а ИТ обладают чрезвычайно высокой динамичностью) оказывает трансформирующее воздействие на природу человека, и такое воздействие не всегда (а, скорее, практически, всегда не-) адекватно осмысливается в процессах подобной трансформации: технология «бежит» впереди человеческой рефлексии. И в самом деле, проблема взаимовлияния развития ИТ (как и нано-, био-, когнитивных технонаук) и социогуманитарной сферы лежит в створе междисциплинарности, методология которой требует специальных компетенций, не обретаемых сегодня в процессе университетского образования.

Примечание . Напомним здесь об относительно новой области знания и методологических подходов – социальной оценке техники , которая является областью не только междисциплинарных проблемно-ориентированных, но и трансдисциплинарных исследований, что означает ее соотнесенность с широкой общественной проблематикой. Эта прикладная область философии техники, получившая за последние десятилетия институциональное оформление, в нашей стране почти совсем неизвестна и мало обсуждается³. Между тем, т.н. «человеческий» фактор в информационной среде играет сегодня гораздо более серьезную роль, чем это было на заре становления сети Интернет. Глобализация ИТ создает пространство неограниченных возможностей воздействия на личность и общество. Воздействия как позитивного характера – в возможностях использования всего богатства мировой культуры для саморазвития, самополагания, самореференции, самоконституирования и пр. Так и негативного характера, проявляющегося в киберпреступности, использующей ИТ и глобальные сети для самых разных преступных целей – вплоть до новой формы терроризма – кибертерроризма.

В инженерной среде распространено убеждение, что проблемы, возникающие вследствие появления новых технологий, могут быть решены посредством технологий следующего, более высокого уровня. Однако цивилизационное развитие свидетельствует о том, что социальногуманитарные проблемы невозможно решить исключительно техническими методами. Поскольку область ИТ представляет собой сложную социотехническую систему, причем систему эмерджентную, с незапланированными свойствами, феноменами или объектами, возникающими неожиданно, постольку ее проблематизация требует не только инженерно-технологического, но и социально-философского подхода.

В этом случае «информатика» интерпретируется как важная социотехническая проблемноориентированная ИТ, конечной целью которой является разработка гибкой платформы предоставления смысловой и ценной информации лицу, принимающему решения, из потока (измерений, наблюдений или обработки) больших неструктурированных данных [3] именуемой в настоящее время как «Аналитика Больших Данных».

В основе данного понимания лежит алгоритмическое представление о процессах вычислений и обработки информации ( тезис Тьюринга-Черча) о независимости результата вычислений от физической природы вычислительного устройства, а модель последовательных вычислений на вычислительном устройстве с архитектурой фон Неймана широко применяется до настоящего времени. Рассмотрим кратко эволюцию данного тезиса в отмеченных задачах построения ИТ.

1.1.    «Инженерная философия» разработки информационных технологий в социотехнических системах

Разработка физических моделей в логике теорий квантовых вычислений⁴, квантовых алгоритмов и квантовой теории информации существенно уточнили тезис Тьюринга-Черча об алгоритмической и логической универсальности процессов вычислений. Было установлено новое явление экспоненциального ускорения вычислений и решения алгоритмически неразрешимых задач в данных ограничениях за счет смены алгоритмического базиса вычислений на физически обоснованную (законами теории относительности, квантовой механики, биофизики, нейрофизиологии и термодинамики) платформу. При этом, обработка информации, сама информация и вычислительные процессы рассматриваются как физические процессы.

Разработки современных моделей ИТ на основе физического подхода изменили инженерную философию теории вычислений и логическую интерпретацию сложности вычислительных алгоритмов⁵, привели к понятию технологий интеллектуальных когнитивных вычислений и к разработке на её основе нового подхода в инженерной философии⁶ – Intelligent System of Systems Engineering – «Интеллектуальные Системы в Системной Инженерии и Аналитике Больших Данных».

В результате было расширено представление об информационных процессах в физическом мире как в пространственно-временном континууме в виде дополненной (физически измеряемой или виртуальной) информационной составляющей. Дано описание нового (параллельно с физическим) информационного пространства с разными информационными метриками для формализации и моделирования процессов обмена информацией между активными агентами [со своими реальными и виртуальными мирами (дополненной реальностью)] (см. Часть 2).

Так, например, современные ИТ разработки интеллектуальной макро- микро- и наноробототехники, функционирующей в различных пространственно-временных континуумах c различной размерностью, являются ярким тому примером. В этом случае, наряду с описанием геометрической метрики физического пространства-времени вводится информационная метрика пространства-времени (на основе, например, количества информации Фишера и его измерения) или обобщенных мер информационной дивергенции и относительной энтропии7,8,9,10, что привело к созданию моделей информационной геометрии11,12,13 и информационной физики14 (см. Часть 2). Для разработки интеллектуальных макро- микро- и нано-роботов и многоагентных систем необходимо физически обоснованное, строго формализованное описание пространственновременных отношений на основе, например, квантовой и релятивистской нечеткой логики, и квантового управления, извлечения скрытой в классических состояниях квантовой информации как дополнительного информационного ресурса для совершения полезной работы (что невозможно на классическом физическом уровне) и т.п.

Примечание . В современных ИТ также применяются в общем виде синергетические эффекты извлеченной информации, например, для формирования новых социальных групп только за счет обмена информацией без физического взаимодействия. На современном этапе развития общественных отношений в социотехнических системах миром правит смысловая и ценностная информация, извлечение и обработка которой дает право быть объективно монополистом принятия решений в определенных секторах информационного пространства и рыночной цифровой экономики ( digital economics ). Такой подход составляет научный базис и программноалгоритмическую платформу информационной теории управления роботизированными социотехническими системами , а объектами управления уже являются взаимодействующие с человеком-оператором коллективы когнитивных (и информационно связанных) автономных роботов нового поколения¹⁵.

Идеология формирования и проверки адекватности физических моделей объектов на основе экспериментальных данных обобщается в виде новой платформы инженерии – информационная когнитивная технология – разработка корректных когнитивных моделей плохо формализованных сложных физических объектов из больших экспериментальных слабоструктурированных массивов данных. В результате возникла обратная расширенная задача Ф. Бэкона: построение теории научного познания и извлечения знаний из интерпретации результатов измерения и наблюдения в виде аналитики больших данных о внешнем мире для разработки когнитивных моделей физических процессов.

Такой подход осуществляется за счет нового инструментария теории искусственного интеллекта – ( computational intelligence toolkit ) глубокого (в общем случае квантового ) машинного обучения и поиска супер-корреляционных связей в базе больших неструктурированных данных, и формирования информативных признаков¹⁶ для проверки физической строгости и корректной адекватности разработанных математических моделей данному исследуемому физическому объекту.

Возросший поток информации привел к необходимости создания аналитики больших данных и к переходу на новые принципы построения интеллектуальных ИТ, основанных на рассмотрении информации как физической переменной, к коренному изменению вычислительного базиса процессов сбора, обработки и передачи больших данных с применением законов квантовой механики, теории относительности, биофизики, нейрофизиологии и термодинамики.

В результате аксиома Тьюринга-Черча об алгоритмическом базисе вычислительных процессов, не зависящем от физической природы вычислительного устройства, был существенно уточнен, а Ландауэр в 1961г. установил физический характер информации и термодинамическую величину стоимости обработки одного бита информации. Это привело не только к экспоненциальному ускорению сложных вычислений на квантовом уровне построения вычислительных устройств, но и к новому эффекту – к решению алгоритмически неразрешимых на классическом уровне задач.

1.2.    Сквозные информационные технологии

Приоритетные в РФ сквозные цифровые технологии официально определены распоряжением Правительства №1632-р от 28.07.2017 г., которым была утверждена программа «Цифровая экономика»: Большие данные ; Нейротехнологии и искусственный интеллект ; Технологии распределенного реестра ; Квантовые технологии ; Новые производственные технологии ; Интернет вещей ; Компоненты робототехники и сенсорики ; Технологии беспроводной связи ; Технологии виртуальной и дополненной реальностей .

Переход развитых стран как социотехнических систем к глобальной разработке цифровой экономики и автоматизации производственных / непромышленных процессов сталкивается с проблемой роботизированного сбора и обработки больших данных, извлечения полезной информации и знаний из обработанных данных и построения корректных моделей интеллектуальных информационных технологий (ИТ) и систем принятия решения в рассматриваемой проблемно-ориентированной области для гарантированного достижения функционирующей социотехнической системой поставленной цели. Решение такой проблемы только созданием программно-алгоритмической платформы на синтаксическом уровне на современном этапе имеет ограниченные возможности эффективного применения.

Примечание . Отметим, что сквозные цифровые технологии – технологии, находящие свое применение в различных областях, например, рыночных секторах экономики. К настоящему времени в силу развития наукоемких сквозных ИТ и взаимодействия человека с компьютером типа «мозг – компьютер – исполнительное устройство – интеллектуальный робот» социум передовых стран погружен в социотехническую систему с новыми законами управления самим социумом за счет извлечения и обмена информацией. Так, например, неожиданным явлением для многих контролирующих административных государственных структур оказались «цветные» революции, которые совершаются без физического выхода её организаторов агитировать на улицу, образуя кластеры забастовщиков (самоорганизующиеся многоагентные системы). Отмеченный эффект формируется только за счет взаимодействия человека с программноаппаратными средствами передачи информации и синергетики от передачи через ИнтерНет необходимой информации и знаний. Это яркий и поучительный пример, когда информация позволяет совершить эффективное действие («полезную» работу), которое по эффективности и количеству значительно превосходит результат от обратного действия – извлечения информации и совершения затем работы (например, агитаторами забастовок).

В этом случае требуется расширение программно-алгоритмической платформы на основе разработки соответствующих интеллектуальных ИТ, основанных на извлечении знаний о внешней среде, в которой функционирует и адаптируется социотехническая система с заданной экономической и политической структурой взаимоотношений и связей, и создание возможности для совершения полезной работы за счет извлеченной и обработанной интеллектуальной ИТ информации. В этом заключается одна из задач разработки сквозных ИТ цифровой экономики.

Примечание . Анализ 30-летнего опыта работы ведущих компаний и университетов развитых стран, разрабатывающих цифровую экономику ( digital economics ), показал, что одно из успешных решений и продуктивное развитие данной проблемы находится в рассмотрении части социума, сознательно погруженного в интеллектуальную роботизированную социотехническую систему на основе указанного перечня сквозных ИТ. Такая система способна самоорганизовываться за счет сбора, обработки больших данных и извлечения из них знаний, как дополнительного информационного ресурса, способного совершать полезную работу на основе контролируемого и управляемого обмена знаниями между человеком-оператором и когнитивными роботизированными системами¹⁷.

1.3.    Интеллектуальные когнитивные вычисления и проблема познания Бэкона

При разработке ИТ цифровой экономики требуются динамически изменяющиеся образовательные процессы для подготовки квалифицированных кадров с новыми знаниями в проблемно-ориентированных областях с перераспределением функциональных нагрузок между роботом и человеком-оператором. В результате возникла острая необходимость в создании когнитивных ИТ интеллектуальных вычислений, позволяющие разрабатывать цифровую экономику на основе познания процессов когнитивной бизнес-аналитики и природных физических процессов в социотехнической системе, решая одновременно такую социально значимую задачу как нехватка квалифицированной рабочей силы и профессиональных кадров для разработки интеллектуальных ИТ. В результате возникает необходимость изучения новых процессов познания внешнего мира, начиная с процессов понимания, например, интеллектуальными роботами пространственно-временных отношений для ориентации в различных метриках пространства-времени и наделенных такими качествами как интуиция, инстинкт и эмоции, или, например, ошибок человека-оператора в непредвиденных / нештатных ситуациях и т.д. Такой процесс познания необходим для построения соответствующих моделей когнитивных процессов прямого извлечения знаний в системах «мозг-компьютер-исполнительное устройство» как нового инструментария формирования моделей извлечения и приобретения знаний.

Такая постановка вопроса позволяет включить интерпретации качественных вычислений ощущений и измерений окружающей среды на основе нестандартных видов вычислений (например, Affective Computing &  Kansei Engineering, Personal Computing, Fuzzy Computing, Social Computing, Qualitative &  Information Physics, Information Geometry и мн. др.) в виртуальном физическом или дополненном логическом пространствах^18,19, которые необходимо включать в базы знаний интеллектуальных ИТ.

Примечание . Современная теория сложности вычислительных процессов утверждает, что если удалось показать, что алгоритм для вычисления, обладающий нужными свойствами, невозможен, то имеет смысл вернуться к постановке задачи и «пошевелить» постановку задачи, т. е. изменить исследуемую функцию (например, сузив область аргументов, точность значений и т. п.) так, чтобы сохранился исходный физический смысл, но упростилось вычисление интересующей нас функции²⁰. В этом случае человек-оператор включен в контур управления и появляется возможность эффективно применить его субъективные (нечеткие) скрытые возможности интуиции, инстинкта и эмоций (особенно в нештатных ситуациях управления объектами особой социоэкономической важности) через извлечение знаний на основе когнитивных устройств как систем с искусственным интеллектом. Такая постановка задачи созвучна с научной проблемой Ф. Бэкона.

В данной статье рассматривается расширенная проблема познания Ф. Бэкона и роль когнитивных процессов познания в разработке образовательных интеллектуальных ИТ для цифровой экономики, например, роботизированных социотехнических систем.

1.4.    Цель работы

В данном цикле работ рассматриваются следующие вопросы:

• -    Прикладные аспекты методологии решения обобщенной проблемы Бэкона в задачах инженерии знаний и построения интеллектуальных систем управления, в частности, управления физическими экспериментами (включая термодинамические, квантовые и релятивистские модели и ограничения на физически корректную интерпретацию логически непротиворечивых результатов больших данных экспериментов).

• -    Обсуждаются также актуальные вопросы разработки эффективных образовательных процессов в области интеллектуальных наукоёмких ИТ на основе сквозных квантовых ИТ и новых видов интеллектуальных когнитивных вычислений.

• -    Рассматриваются, в частности, сложные для цифровой экономики вопросы формирования и научного обоснования сквозных образовательных процессов нового класса специалистов в области наукоёмкой ИТ – в квантовой релятивистской информатики и квантового программирования для интеллектуального роботизированного управления физическими установками и экспериментами (например, в мегапроекте NICA – ионный коллайдер – Nuclotron based Ion Collider Facility (NICA)). Подчеркнем, что в мегапроекте NICA применяются практически все из перечисленных приоритетных в РФ направлений развития сквозных цифровых технологий.

• -    Связь проблемы Ф. Бэкона с задачами извлечения знаний из больших экспериментальных данных и роль когнитивных процессов познания в разработке образовательных интеллектуальных ИТ для цифровой экономики роботизированных социотехнических систем.

• 3.    Проблема Ф. Бэкона познания и интерпретации извлеченных знаний в технологиях интеллектуальных моделей вычислений21

2.1.    История проблемы Бэкона 3.2.  Математическая модель и содержательная физическая интерпретацияее физической реализации

В частности, обсуждается проблема («идола рода» и «идола пещеры») познания физического процесса эмпирическим путем в новой логике научного познания различных законов физического макро- и микромира, описывается роль физических и логических ограничений (часть 1). Общее решение расширенной проблемы основывается на аппарате нечеткой когнитивной логики для 3 D -макромира (и квантовой релятивистской нечеткой логики для релятивистского 4 D -микромира) физической интерпретации научного эксперимента с применением роботизированных систем обработки извлеченных знаний из аналитики экспериментально полученных больших данных (часть 2). Решение обобщенной проблемы Бэкона приводит к формированию обоснованных корректных моделей мысленных и реальных экспериментов физических процессов и научному прогрессу в изучении основ фундаментальной науки (часть 3). Обсуждается проблема построения роботизированных социотехнических систем с «дружелюбными» когнитивными интерфейсами на основе систем «мозг-компьютер-исполнительное устройство» и виртуальной (дополненной) реальности для формирования образовательных / учебных процессов в лабораторных условиях и НИР в области наукоёмких ИТ как гибридных систем с искусственным когнитивным интеллектом (часть 4).

В связи с перечисленными целями рассмотрим кратко сущность самой проблемы Бэкона.

Свою задачу в науке Ф. Бэкон видел в том, чтобы превратить процесс научного познания в практическое занятие, совершающееся при опоре на человеческие способности: разум , воображение и чувства . С точки зрения современного естествознания это означает, что интерпретации результатов мысленного эксперимента или наблюдений недостаточно для установления адекватности результатов модели суждений свойствам реального объекта, необходимо проводить эмпирические исследования, которые подтверждают или опровергают экспериментально выдвинутые доводы.

Результаты мысленного эксперимента должны иметь ясную научную (логическую и физическую) интерпретацию. Ф. Бэкон был родоначальником материалистических основ логики Нового времени. Также его можно считать родоначальником материализма и эмпиризма. Он резко критиковал силлогистику Аристотеля и средневековую схоластику, которую он называл бесплодной и оторванной от реальности.

По существу предмета обсуждения Ф. Бэкон был первооткрывателем такого взгляда на окружающий мир. Как и перед любым ученым, перед ним стоял ряд фундаментальных задач и вопросов, на которые в свое время он не смог найти ответ. Однако ему удалось заложить направление движения мысли на многие века вперед. Вопрос с логикой научного познания так и не был решен им, он лишь указал движение развития. В то время еще глубоко не исследовали работу мозга, что движет мыслью в головном мозге, а сам процесс познания, мышления и интерпретации эксперимента имеет особенности квантовой природы22. К тому же, Бэкон не оперировал такими терминами как модель, система управления, отсутствовал системный и комплексные подходы. В дальнейшем идеи Ф. Бэкона были подхвачены и развиты такими исследователями как Джон Локк, Давид Юм и Герберт Спенсер. Саму основу научного метода заложил Огюст Конт. Французский мыслитель сформулировал основные принципы верифицируемого научного знания. Его идеи в дальнейшем продолжил Карл Поппер, сделавшего фальсификацию, а не верификацию подлинной проверкой гипотезы.

Поясним некоторые особенности теории моделей применительно к рассматриваемой проблеме Бэкона:   построения корректных формализованных моделей логически непротиворечивых суждения о физических свойствах объекта.

Для того чтобы математический результат мог быть воспринят, необходима его качественно содержательная интерпретация [4, 7, 8, 15, 16]. Именно введение такой интерпретации дает возможным считать математические конструкции, полученные по второму способу (т.е. постулированные вне связи с какими-либо физическими объектами), моделями реальных объектов23. Следовательно, введение содержательной интерпретации дает возможность установить способность и способ физической реализуемости математической модели. Поэтому, более корректным и общим определением24 математической модели будет следующее: Математическая модель – это формальная система, представляющая собой конечное собрание символов и совершенно строгих правил оперирования этими символами в совокупности с интерпретацией свойств определенного объекта некоторыми отношениями, символами или константами.

Примечание . Подчеркнем еще раз, что в математике совокупность переменных, констант и отношений представляет собой абстрактный математический объект и именно интерпретация делает его математической моделью реального объекта. Следует обратить также внимание на следующий факт из теории множеств^{25, 26}. Замена моделей интерпретацией возможна в условиях *

финитной метатеории. В этом случае интерпретация теории T в теории T определяется как *

конечная последовательность формул T , в которой каждая формула соответствует точно одному из неопределяемых отношений теории T и имеет столько свободных переменных, сколько аргументов в соответствующем отношении. Для простоты предполагается, что все исходные понятия теории T являются отношениями. Если атомарные формулы заменить соответствующими формулами из интерпретации, то аксиомы теории T должны быть теоремами из теории

_T * _.

Все эти результаты доказуемы в финитной метатеории в предположении, что все обсуждаемые теории конечно аксиоматизируемы. Для бесконечной системы аксиом даже определение интерпретации требует уже относительно сильной метатеории. Поэтому доказательства теорем типа совместности и существования моделей необходимо использовать теорию Цермело – Френкеля. Тогда предоставляется возможность использования понятий и результатов теории моделей непосредственно, избегая перехода к интерпретации.

Обсуждение основных положений качественного анализа в теории систем показывает, что построение качественно содержательной интерпретации может проводиться на физическом, сенсорном (чувственном) и прагматическом (ценностном) уровнях при сохранении общего формализма исследования объекта. Поэтому рассматриваемую проблему следует сформулировать следующим образом: можно ли для данной абстрактной математической модели системы найти такую содержательную интерпретацию, которая не противоречила бы известным физическим законам на заданном уровне знаний (и, в первую очередь, наиболее общим из них – законам термодинамики).

Другими словами, можно предложить следующую формулировку: допускает ли данная математическая модель системы такую содержательную интерпретацию, которая могла быть материально реализована, т.е. физически осуществима . Ясно, что если не существует содержательной интерпретации данной математической модели, совместимой с физическими законами, то материально реализовать эту модель невозможно. В определенном смысле данная проблема является обратной проблемой познания Бэкона.

Характерной чертой расчетной модели в более общем случае является введение некоторых функционалов от изучаемых процессов. Экстремальные значения этих функционалов служат показателем оптимальности или эффективности процесса. Большое значение имеет принцип минимальной сложности аппроксимирующих моделей исследуемых процессов. Существенным требованием является сходство модели с объектом, которое можно определить на основе понятий порогов различимости и максимуму взаимного количества информации, содержащегося в расчетной модели относительно физического объекта.

3.3.    Решение проблемы «идола рода» и «идола пещеры»

Проведение эксперимента позволяет преодолеть еще один барьер, который увидел Ф. Бэкон в человеческой природе, которая не дает разуму четко моделировать идеи. Это, как их называет Ф. Бэкон, – «идолы» или врожденные особенности человеческой природы.

В « идоле рода » он излагает идею антропоморфизма. Это означает, словами Бэкона, отождествление собственной природы с природой вещей. Другими словами, считать истинным, то, что видят и чувствуют наши органы чувств. Эта позиция часто ошибочна на классическом уровне восприятия физических процессов, но используется в некоторых моделях немонотонного нечеткого логического вывода.

О явлении « идол пещеры » Бэкон писал следующее: «Человеческий разум не сухой свет, его окропляют воля и страсть, а это порождает в науке желательное каждому». Это индивидуальные склонности и предубеждения, которые препятствуют объективно смотреть на вещи. Чтобы не попасть в ловушки собственного разума, необходимо подтверждение выдвинутой гипотезы эмпирическим путем или экспериментом.

Как показала квантовая теория измерений наблюдения и квантовые измерения разрушают состояние квантовой системы, а интерпретация результатов содержит своего рода субъективный характер (свобода воли – free will freedom [of measurement result interpretation])^27,28 из-за объективного присутствия принципа неопределенности Гейзенберга. Более того, интерпретация результатов самой квантовой теории наблюдателем (активным агентом), использующего в своей аргументации систему аксиом квантовой теории, неполна и находится в противоречии²⁹ с логическим выводом другого наблюдателя (обобщенный Wigner’s Friend Paradox – Вигнеровский парадокс друга). Таким образом, является физическим аналогом теоремы Геделя о неполноте доказательства математической теории средствами самой теории (см. ниже).

Примечание : О моделях управления когнитивными процессами в коре головного мозга . В конце 20 века подошли к решению проблем Ф. Бэкона со стороны работы мозга, был сформирован современный физически обоснованный научный логический инструментарий, изучены особенности головного мозга в виде искусственных нейронных сетей³⁰, излучающих управляющий электрический сигнал со смысловым значением соответствующего узла нейронной сети или отдельного нейрона^31,32. При этом сигналы электроэнцефалограммы, снятая из зоны или с отдельного нейрона, отвечают за эмоции, инстинкт, интуицию, ненависть, любовь и т.д.

Примерно с середины 1990х годов началось синергетическое соединение результатов нейрофизиологии, теории искусственного интеллекта и теория интеллектуального управления, которые позволяют управлять объектом («субъект-объект»)³³. Это привело к тому, что появились понятия BСMI (« brain – computer – machine interface ») – интерфейс «мозг-компьютер-исполнительное устройство». Появились расшифровки смыслового электроэнцефалограмм, регистрируемых с коры головного мозга.

Это привело к тому, что появился другой взгляд на моделирование когнитивных процессов и к новому виду интеллектуального когнитивного управления34.

В этом случае не используется информация и знания о свойствах объекта управления, не применяется классическая система управления исполнительным устройством. Применяя новый интеллектуальный инструментарий в виде оптимизатора баз знаний (на технологиях интеллектуальных вычислений - мягкие и квантовые вычисления) извлекается информация из электроэнцефалограммы и формируются знания в виде конечного числа продукционных правил принятия решения. Это вылилось в теорему об универсальном аппроксиматоре, содержащий полную и адекватную информацию об основных качественных особенностях исследуемого объекта, не прибегая к построению его модели. Можно не знать все свойства системы. Теперь можно управлять, например, автономным роботом, минуя классическую систему управления, своими когнитивными способностями. Получился синергетический эффект: при применении в совокупности различных знаний получен технический эффект, который эти знания не давали по отдельности.

Программное обеспечение и базы знаний, позволяют решить проблему как мысленный эксперимент можно превратить в физическую реальность и совершить полезную работу за счет извлеченной информации и знаний о желаемом управлении. Программное обеспечение позволяет корректно интерпретировать управляющий сигнал в виде электроэнцефалограммы с коры головного мозга в виде логического построения продукционных правил и перевести команду управления (желание исследователя) роботом, минуя изучение его свойств по Бэкону.

Был подробно рассмотрен вопрос: как при помощи сформированных баз знаний и их взаимодействия роботизированные системы в автоматическом режиме решают задачи, самоорганизуясь в информационном (не физическом) пространстве35. На этом примере можно утверждать, что современные интеллектуальные роботизированные системы достигли в своей области определенных успехов, которые позволяют по новому изучать опыт природы и окружающий нас мир. Тут стоит обратить внимание на два момента. Первый, это существование сквозных ИТ, при помощи которых были достигнуты такие успехи и второй, как взаимодействие автоматизированных интеллектуальных роботизированных систем и человека помогают изучить окружающий нас мир.

В современном мире активно развиваются технологии связанные с роботизированными системами, нейронными сетями и искусственным интеллектом. Своим появлением эти технологии обязаны теории мягких и квантовых вычислений, робастным базам знаний, теории квантовой механики, квантовой релятивисткой информатики. Все это в совокупности продвинуло человеческую мысль и позволило решить поставленные Ф. Бэконом проблемы.

В данной Части 1 общей работы предлагается методология определения корректной математической и физической моделей на основе извлечения знаний из поведения системы на макроуровне. Свойства моделей на макроуровне не меняются при измерении или не меняют свое состояние при наблюдении поведения объекта. Решение вопроса на макроуровне средствами интеллектуальных когнитивных вычислений корректно и позволяет не вступать в противоречия с идеями Ф. Бэкона.

3.4.    Фундаментальные сдвиги в науке как подтверждение идеи Бэкона о «свете опыта природы, который вечен»

В науке важно не то, когда и кем открыта та или иная истина, авторитет древности не должен стеснять прогрессивное развитие науки, которое движется вперед. «Истину надо искать не в удачливости какого-либо времени, которая непостоянна, а в свете опыта природы, который вечен»36. Ф. Бэкон выдвинул тезис о том, что наука не стоит на месте. С развитием человеческой мысли опровергаются ранее выдвинутые гипотезы и теории, которые были актуальны в свое время, однако, с течением времени, мы видим, что им на смену приходят другие, более точно отражающие окружающий нас мир. И то, что раньше казалось невообразимым, приходит на смену уже устоявшимся представлениям. Мысленное управление роботом, еще в недалеком прошлом являлось лишь, дерзким предположением. Однако, уже сейчас, это новое слово в науке, которое позволяет пересмотреть не только прикладные возможности человека, но и фундаментальные научные представления.

Описанные выше теоретические разработки делались на стыке различных наук: информатики, математики, психологии. Синергетический эффект такого взаимодействия позволил решить различные задачи перед исследователями. Это позволило еще глубже приблизиться к пониманию законов и обустройства природы. В данный момент происходит переход от неклассическая научной картины мира к пост неклассической. Перечислим некоторые онтологические постулаты, которые сформировались к этому времени в связи с развитием идей теории искусственного интеллекта и технологий аналитики больших данных:

• -    В реальном мире не существует изолированных и самодостаточных объектов и систем.

• - Все объекты и системы в мире изменяются, но их изменения носят эволюционный

характер.

• -  Со временем все системы исчерпывают свои энергетические возможности (согласно

второму закону термодинамики) и становятся неустойчивыми.

• -    Все сверхсложные системы ведут себя вероятностным образом. Они потенциально готовы ответить на внешние и внутренние изменения и воздействия. Их поведение имеет нелинейный характер. Они готовы эволюционировать в разных направлениях, отправляясь от одного конкретного состояния в другое устойчивое через бифуркацию.

• -    Прогрессивное развитие объектов и систем, в течение длительного времени, возможно за счет притока и потребления энергии извне, из внешней среды, окружающей эти объекты.

• -    Мегамир, то есть объекты и системы космического масштаба и Вселенная в целом, являются сверхсложной физической, вычислительной и логической системой, подчиняющейся в ходе своей эволюции законам изменения открытых, диссипативных и нелинейных систем.

• -    Модель Вселенной допускает эквивалентное многомировое описание пространственновременного континуума квантовой релятивистской механики (типа введенной Эвереттом и Де Виттом³⁷) и интерпретацию пространственно-временных событий и причинно-следственных связей в виде информационной модели³⁸.

• -    Преимуществом введения описания двух эквивалентных (физической и информационной) моделей пространственно-временного континуума Вселенной даёт возможность обойтись без постулата редукции – его место занимает предположение о множественности физических и информационных миров и о том, что в момент измерения производится выбор одного из них. При этом метрики физического и информационного пространства времени позволяют дать эквивалентное инвариантное описание хронологии передачи информации из одной точки событий пространственно-временного континуума в другую с учетом вида и типа преобразования систем отсчета наблюдателя^{39, 40}.

• -    Вселенная и головной мозг человека-оператора (с точки зрения теории искусственного интеллекта) являются самоорганизующейся и саморазвивающейся вычислительной системой с обменом информацией, рассматриваются (как новая когнитивная платформа вычислительного ресурса аналитики больших данных) в виде квантового компьютинга⁴¹ с новым интеллектуальным инструментарием (глубокое квантовое машинное обучение на квантовых нейронных сетях, оптимизация на основе квантовых генетических и эволюционных алгоритмах и мн. др.).

3.5.    Информационно-термодинамические условия и ограничения на возможность совершения полезной работы за счет извлеченной информации (обратная проблема Бэкона)

Таким, образом, можно подтвердить тезис Бэкона о том, что со временем ранее положенные в основания научного здания гипотезы пересматриваются и на их месте возникают новые представления об окружающем мире.

Современная физика (феноменологическая термодинамика) утверждает (и справедливо), что необходимо совершить полезную работу для извлечения информации о поведении исследуемой системы, затратив при этом дополнительный энергетический ресурс (потеряв полезную работу за счет возрастания энтропии в поведении исследуемого объекта и системы измерения извлекаемой информации – физический закон интеллектуальной ИТ образовательного процесса). В этом случае справедливы42 следующие информационно-термодинамические ограничения:

W e ^S xt ≤-∆ F^S + k B TI ,    W c ^S os t ≥ k B TI

где W ^S означает количество извлекаемой работы из системы S и определяется количеством (квантово-классической взаимной) информации I , которая является мерой точности измерений и знаний о системе S и ограничено сверху; аналогично W ^S ограничено снизу и означает полную стоимость измерения и считывания информации; величина Δ F ^S означает свободную энергию системы S ; величина kT ln2 ( T – температура и k – постоянная Больцмана) означает количество работы, которое можно извлечь из термодинамического цикла и затратить на считывание одного бита информации (Ландауэр, 1961г.). Таким образом, согласно (1), существуют объективные границы на количество извлекаемых знаний из измерений поведения исследуемой системы, а знания позволяют совершать полезную работу.

Пример : Информационно-термодинамические оценки затрат ресурса на извлечение количества знаний из процессов измерения. В микросистемах термодинамические величины, такие как «работа», «тепло» и «внутренняя энергия» не являются постоянными величинами и флуктуируют. Случайные флуктуации могут нарушать второй закон термодинамики, но в среднем второй закон термодинамики на макроуровне выполняется, если начальное состояние системы находится в тепловом равновесии, т.е. ∆ F - W ≤ 0 , где, как и ранее ∆ F – свободная энергия, как мера различия между состояниями системы, W – совершаемая работа и знак означает усреднение по ансамблю множества состояний системы. Однако управление с обратной связью позволяет целенаправленно, выборочно манипулировать только флуктуациями так, что выполняется строгое неравенство ∆ F - W > 0 . Данное выражение эквивалентно использованию информации о поведении системы⁴³, прототип демона Максвелла. Термин «обратная связь» означает, что выбор стратегий управления зависит от результатов измерений на выходе системы управления. Другими словами, метод «управление с обратной связью» эквивалентен применению «систем управления с замкнутым контуром». Применение управления с обратной связью позволяет использовать информацию в качестве ресурса в виде свободной энергии системы⁴⁴. Отметим, что Сцилард разработал модель преобразования одного бита информации в свободную энергию (или работу) в количестве kT ln2 . Таким образом, второй закон термодинамики обобщается в виде ∆ F - W ≤ k TI . Здесь I означает количество взаимной информации, извлеченной измерением состояния системы, т.е. является величиной объективной.

Следовательно, Демон Максвелла (по типу Сцилларда) способен оценить вход (используемое содержание информации) и выход (приобретенную энергию) при управлении с обратной связью и реализует идею преоразования информации в энергию и является информационнотермодинамическим решением обратной проблемы Бэкона.

Пример: Взаимное количество информации и стоимость производимой полезной работы . Законы квантовой механики и термодинамики существенно меняют структуру информационных технологий процессов сбора, считывания и обработки информации⁴⁵. Например⁴⁶, квантовое обобщение классического определения количества взаимной информации S ( A : B ) через количество совместной информации S ( A, B ) и количество информации отдельных событий S ( A ) и S ( B ) в виде S ( A : B ) = S ( A ) + S ( B ) - S ( A , B ) не разделяет квантовую (запутанные состояния) и классическую корреляции, т.е. согласно Cerf & Adami⁴⁷ квантовая взаимная информация S ( A : B ) является одновременно мерой общей корреляции. Более того, S ( A : B ) имеет дополнительную важную интерпретацию в квантовой термодинамике⁴⁸: взаимное квантовое количество информации пропорционально стоимости производимой из начального состояния «тепловой бани» системой работы. В этом случае максимальное количество корреляции измеряется и эквивалентно взаимной информации, которая может быть между двумя не взаимодействующими системами, находящихся в начальном состоянии с температурой T и способной совершить потенциально работу W в виде S ( A : B ) = W / T (в единицах измерения h = k_B = 1 ). Квантовое количество информации, как и в классическом варианте положительная величина, т.е. S ( A : B ) > 0 , но в отличие от классического варианта 0 <  S ( A : B ) < min [ S ( A ) , S ( B ) ] в квантовом случае имеем 0 <  S ( A : B ) <  2 min [ S ( A ) , S ( B ) ] .

Приведенное неравенство следует из определения S (A: B) и «неравенства Araki-Lieb» в виде |S (A)- S (B)|< S (A, B). Перевод определения условной энтропии в квантовую область привносит дополнительные особенности квантовой термодинамики и выделение роли наблюдателя в термодинамике: в зависимости от уровня знаний наблюдателя (на уровне макро-, микро- или нано-уровня наблюдений) определение положений термодинамики зависит от относительного наблюдателя, а определение и выбор самих законов термодинамики зависят от ситуаций подобных демону Максвелла49. Таким проблемы Бэкона.

образом, имеем дополнение к обобщению

Пример: Условная отрицательная квантовая энтропия определяется оператором плотности рАВ

энтропия . Обобщенная квантовая условная в Гильбертовом пространстве в следующем

виде: S ( A|B ) = S ( A,B ) - S ( B ) и, следуя данному определению, как и в классическом случае, определяется соотношение квантовой взаимной информации S ( A : B ) = S ( A ) - S ( AB ) и верхняя граница для квантовой условной энтропии определяется по аналогии с классическим вариантом. Так как S ( A,B ) < S ( A ) + S ( B ) и получим S ( AB ) < S ( A ) по аналогии с классическим вариантом. Однако определение нижней границы резко изменяется по отношению к классическому варианту. В квантовом случае получаем «странный» результат появления отрицательной условной энтропии . Так, например, для чистого состояния (состояние с максимальной супер-корреляцией - запутанное состояние) | ^ -^ ^ "| имеем S ( р ") = 0 , т.е., совместная энтропия равна нулю. В то же время частная локальная энтропия

S ( Tr_A ( p ) ) = log ( 2 ) , т.е. максимальна, а выражение для условной энтропии принимает следующее значение: S ( A B ) = — log ( 2 ) <  0 принимает отрицательное значение. В общем случае, условная энтропия ограничена частными значениями (маргинальных) энтропий в виде — S ( B ) <  S ( AB ) <  S ( A ) . Данный факт характеризует принципиальное различие между классическим и квантовым вариантами теории информации.

Возникшее новое понятие отрицательного значения условной энтропии привело к появлению новых возможностей передачи информации. Было обнаружено, что положительные значения S ( A : B ) определяют частную информацию в кубитах, которую необходимо передать от A к B , а отрицательное значение условной энтропии указывает на существование избыточных кубитов, позволяющие повысить успешную передачу информации.

Рассмотрим еще один пример, характеризующий особенности квантовой информации.

Пример : Коррелированные квантовые состояния с памятью и производство работы при отрицательной условной энтропии . Диссипация тепловой энергии является нетривиальным явлением, когда начальное состояние системы является смешанным состоянием и описываеся оператором плотности p . В квантовом режиме смешанные состояния могут рассматриваться редуцированные состояния глобальных состояний, p_SM , системы S и памяти M и P s = ^Tr M [ Pm ] . Рассмотрим случай, когда наблюдатель может оперировать как системой, так и памятью. Во время глобального процесса локальное состояние системы считывается, p H |0), в то время как локальное состояние памяти p = Tr [ p_M ] не изменяется. Однако процесс считывания использует корреляции памяти с системой и можно в результате применения коорреляций извлечь максимальное количество работы W m ™^ = — k_BTS (§ | M ) . Здесь

S (S M )

S (s M )

условная энтропия фон Неймана между системой и памятью,

^p SM

I = S (pM ) — S (pM ). Условная энтропия может быть отрицательной для квантовых коррелированных состояний (подмножество множества запутанных состояний) и создаются

условия извлечения положительной работы. Этот результат находится в противоречии с принципом Ландауэра в обоих классическом и квантовом состояниях, когда доступна такого рода информация от корреляции состояний.

Возможность извлечения во время считывания информации дополнительной работы носит чисто квантовый характер и основан на новом виде доступной информации, т.е., для практического получения положительной работы требуется знание и доступ к начальному запутанному совместному состоянию системы и памяти и иметь реализацию чувствительного процесса управления степеням свободы обоих частей единой системы. Запутанное состояние между системой и памятью во время процесса разрушается и рассматривается как дополнительный информационный ресурс для извлечения работы.

Такая интерпретация информации сыграла существенную роль при реконструкции самих моделей квантовой механики50,51 и обосновании основ квантовой физики52,53.

Следовательно, результаты квантовой термодинамики и квантовой теории информации, сменив модель и физическую интерпретацию пространства-времени, утверждают, что из

• ⁵⁰    Höhn P.A. Toolbox for reconstructing quantum theory from rules on information acquisition // arXiv:1412.8323v9 [quant-ph] 12 Mar 2018.

• ⁵¹    Jaeger G. Information and the reconstruction of quantum physics // Ann. Phys. (Berlin), 2018. – No 1800097 (1 of 14).

• ⁵²    D'Adriano M., Chiribella G., Perinotti P. Quantum theory from first principles. - Cambridge, UK: Cambridge University Press, 2017.

• ⁵³    Masanes ., Müller M.P., Augusiak R., Pérez-Garcí D. Existence of an information unit as a postulate of quantum theory // Proc. National Acad. Sci. USA (PNAS), 2013. – Vol. 110 - No. 41. – Pp. 16373-16377.

заданного извлеченного количества информации можно получить максимально полезную работу (утверждение « проинформирован - значит вооружен » имеет количественную квантовую оценку), которая может превосходить количество полезной работы, потраченной на извлеченное данного количества информации. При этом, локально, квантовая термодинамика разрешает нарушать второй закон термодинамики^54,55. Более того, Ландауэр установил, что информация и процессы вычислений носят не только алгоритмический, но и физический характеры⁵⁶.

Все известные, например, корректные квантовые релятивистски инвариантные уравнения могут быть выведены из принципа минимума количества информации Фишера (информационная физика), не прибегая к знаниям законов квантовой релятивистской физики и процессам измерения, и составляют основу квантовой информатики и сквозных квантовых технологий.

Примечание . Введение обобщенных мер энтропии Шеннона и количества информации Фишера, Реньи, Тцалиса, Вигнера-Янесе-Дайсона и мн. др., и разработка соответствующих квантовых аналогов^{57,5859,60,61,6263} привело к выводу и обобщению основных соотношений неопределенности Гейзенберга-Шредингера^64,65, обобщению термодинамического соотношения неопределенности «энергия-температура» Бора⁶⁶, обобщения законов квантовой термодинамики с учетом корреляции⁶⁷, определения скорости квантовой эволюции Маргулиса-Левитина⁶⁸, метрик пространственно-временных континуумов^69,70 и многих других квантовых и релятивистских эффектов, исходя из определения мер количества информации как исходного постулата информационной геометрии и информационной физики (см. Часть 2 и 3).

В этом случае информация в определенном смысле первична , а создаваемая за ее счет материя и полезная работа вторичны . Этот тезис определяет решение обратной проблемы Бэкона.

Примечание . Подчеркнем, что ИТ стали самым коммерчески привлекательным товаром на интенсивно развивающемся конкурентном рынке интеллектуальных продуктов, а привлечение методов теории искусственного интеллекта (таких как глубокое машинное обучение, технологи интеллектуальных вычислений и мн. др.) со сменой платформы вычислительного базиса дало возможность получать решения задач, которые ранее были алгоритмически неразрешимыми проблемами. Так, например, решение проблемы оптимального поиска в базе больших неструктурированных данных без привлечения квантовых поисковых алгоритмов (типа алгоритма Гровера) решить невозможно, а сам алгоритм поиска является оптимальным. В этом случае возникает новая проблема обучения специалистов в области разработки ИТ с привлечением методов квантовой механики, термодинамики, теории относительности, теории искусственного интеллекта, теории высокопроизводительных параллельных вычислений, ГРИД-технологий и др.

Традиционные подходы к разработке информатики как методологии и инструментария программно-аппаратной поддержки алгоритмов и средств обработки больших массивов неструктурированных данных ( Big Data &  Data Mining ) информации столкнулись, с одной стороны, с проблемой ограниченных возможностей классических алгоритмов (в частности, с отсутствием эффективных истинно параллельных алгоритмов). С другой стороны, исследуются предельные возможности аппаратных средств обработки информации на основе нанотехнологий. Этот эффект определяется границами применяемых классических методов физики, математики, биофизики и мн. др. в разработке вычислительных алгоритмов обработки информации.

Для разрешения указанных (и многих других) проблем и возникшей необходимости объективного установления предельных границ возможностей информационных процессов обработки данных в последнее десятилетие данного столетия наукоемкие ИТ стали широко применять законы квантовой механики, теории относительности, термодинамики, биофизики, технологии интеллектуальных вычислений и мн. др. В результате был уточнен тезис и расширен постулат Тьюринга-Черча (1936-1937 гг.) о независимости процессов вычислений от изического устройства, на котором выполнялись вычисления.

Более того, согласно Ландауэру (1961г.), каждый шаг вычислений требует энергетических затрат и информация носит не только алгоритмическую, но и физическую природу, позволяющая совершать действие и полезную работу. Установленные соотношения между производством энтропии, количественными мерами информации (Фишера / Шеннона / Реньи / Тцаллиса и др.), потерями полезного ресурса и возможностью совершать полезную работу за счет извлеченной информации и знаний при обработке данных, позволяют по новому осуществлять разработку программно-алгоритмической и аппаратной поддержки процессов сбора, обработки и передачи данных, извлечения знаний из больших массивов количественных неструктурированных данных.

В свою очередь, промышленное освоение ИТ нанотехнологий привело к необходимости развития теории и систем квантового робастного управления, что существенно изменило представление о таких фундаментальных понятиях теории управления как обратная связь, измерения ошибки управления, взаимодействия объекта управления с квантовым регулятором, управления по возмущению, по отклонению, комбинированному управлению, понятия фазового пространства состояний и мн. др.

• 4.    Зачем необходимо учитывать и вводить в образовательные модели сквозных ИТ информатики (computer science) определения физических возможностей и логических ограничений

3.1. Цель учета в образовательных процессах в области сквозных ИТ физических, вычислительных и логических моделей

Квантовая релятивистская нечеткая логика (как особый класс немонотонных логик) и квантовая релятивистская теория информации как физическая теория содержат результаты нестандартного логического вывода и суждений, которые противоречат основным понятиям Булевой логики и классической теории информации Шеннона. Одно из обстоятельств закономерного интенсивного развития наукоемких сквозных ИТ интеллектуального робастного управления в компьютерных нанотехнологиях связано с известным фактом появившейся возможности для системной инженерии доступного (для использования в проектировании) изложения квантовых и релятивистских макроэффектов, которые лежат в основе управления от космическими летательными аппаратами (КЛА), до квантовых систем, находящихся под действием слабых гравитационных полей и гравитационных волн и которые используются интенсивно в современных интеллектуальных сквозных ИТ.

Примечание . Существует обширная (к настоящему времени почти необозримая) журнальная, учебная и монографическая литература по основам и приложениям квантовой механики. Однако, ввиду многообразия абстрактных математических моделей самой квантовой механики и существующих многочисленных противоречий, возникающих при их физической интерпретации, образовательная программа для обучения студентов и инженеров-исследователей, не специализирующихся в области теоретической физики, требует наглядного и ясного описания реальных разработок с экспериментальным подтверждением и интерпретацией теоретических результатов в области теории относительности, квантовой механики и квантовой термодинамики. Выполнение данного условия необходимо для формирования инженерных навыков системного проектирования квантовых устройств, наноэлектроники и практического применения новых видов интеллектуальных вычислений типа квантовых мягких вычислений в интеллектуальных ИТ.

Данное требование, в первую очередь, относится к прорывным образовательным программам для широкой аудитории в области квантовой информатики, нанотехнологий, квантового интеллектуального управления, квантового программирования и квантовых вычислений, разработки и проектирования устройств наноэлектроники, наноробототехники и наномехатроники и мн. др. Такого рода образовательные программы формируются параллельно с разработкой новых результатов и сами пользователи участвуют непосредственно в данном процессе формирования знаний.

Поэтому в данной серии статей основное внимание сосредоточено на методологии изложения основ квантовой релятивистской механики и информационно-термодинамического подхода к оценке корректности и границ применимости разрабатываемых моделей ИТ с иллюстрациями на конкретных примерах и интерпретацией экспериментальных результатов из указанных проблемно-ориентированных областей для студентов и системной инженерии компьютерных нанотехнологий ( computer science ), управления, робототехники и интеллектуальных ИТ, инновационного инженерного менеджмента, основанного на знаниях.

Квантовая релятивистская информатика как физическая и математическая теория построения программно-алгоритмической и аппаратной поддержки процессов обработки данных и передачи информации является обобщением и развитием традиционных методов и подходов информатики, опирается на новые физические представления моделей информационных процессов сбора, обработки и передачи данных с привлечением и учетом квантовых, термодинамических и релятивистских эффектов. При этом, вследствие объективной необходимости, учитываются как физические ограничения, так и информационно-термодинамические пределы на разрабатываемые (физически реализуемых) моделей процессов обработки и передачи информации. Поэтому в данной статье в первую очередь обсуждаются методология построения и классификация моделей, возможности и подходы проверки на логическую и физическую непротиворечивость физически реализуемых моделей информационных процессов.

Разработка и развитие новых ИТ основаны на достижениях фундаментальных наук в области физики, математики, биофизики, нейрофизиологии мозга, биологии, теории искусственного интеллекта, теории управления, теории сложных слабоструктурированных систем и мн. др. Однако многие из полученных результатов в области фундаментальных наук не до конца востребованы инженерией системного проектирования в силу трудности восприятия и практического применения данного результата или, с другой стороны, недооценкой менеджерами промышленных компаний прикладной стороны и коммерческой привлекательности полученного интеллектуального продукта на рынке ИТ. Рассмотрим актуальность обсуждаемой проблемы и коммерческую привлекательность разрабатываемых интеллектуальных продуктов на современном этапе развития наукоёмких ИТ с позиции инженерного менеджмента, основанного на знаниях71.

Содержательную часть и доказательную базу наукоёмкости рассматриваемых моделей ИТ приведем на примерах. Примером одной из практических целей разработки наукоемких ИТ является коммерчески привлекательный и конкурентно способный программно-аппаратный комплекс, а также промышленный инструментарий проектирования интеллектуальных систем управления (ИСУ) физическими моделями сложных слабоструктурированных объектов в нештатных ситуациях. Проектирование интеллектуальных встраиваемых когнитивных контроллеров для надежной корректировки ошибок и восстановления информации в процессах обработки больших массивов данных физических экспериментов является еще одним примером подобного рода коммерчески привлекательных интеллектуальных продуктов.

Исследования и практика разработки систем управления физическим экспериментом показали следующее: проектирование, развитие и реализация эффективных высоких наукоемких ИТ (создаваемых в различных областях науки и техники) неразрывно связаны с необходимостью развития и повышения уровня интеллектуальности используемых моделей процессов и систем управления, объективно учитывающих в законах эволюции контекстуально-зависимые физические эффекты, термодинамические ограничения и информационные границы, реально существующие в конкретных моделях реальных объектов.

В данной работе рассмотрена проблемно-ориентированная область разработки наукоемких ИТ:  прорывные инновационные ИТ интеллектуального управления квантовыми и релятивистскими системами в компьютерных нанотехнологиях с целью показать перспективность данной технологии при разработке коммерчески привлекательных интеллектуальных продуктов в области робототехники, космической техники, квантового управления в нанотехнологии, информационно-управляющих комплексов социально и экономически значимых объектов, квантовой криптографии и квантовых облачных вычислений «вслепую» (quantum blind cloud computing) для защиты информации и безопасности систем, квантового распознавания объектов в условиях помех, квантовый интернет и др.

4.2.    Особенности когнитивных образовательных процессов с учетом строгости физических и корректности логически непротиворечивых моделей

Одно из обстоятельств закономерного интенсивного развития наукоемких ИТ интеллектуального робастного управления в компьютерных нанотехнологиях связано с известным фактом появившейся возможности для системной инженерии доступного (для использования в проектировании) изложения квантовых и релятивистских макро эффектов, которые лежат в основе управления как космическими летательными аппаратами (КЛА), так и квантовыми системами, находящихся под действием слабых гравитационных полей.

С точки зрения теории управления и системной инженерии, проектирование, например, КЛА, движущегося в искривленном пространстве-времени под действием солнечного ветра или мелких метеоритов как случайных воздействий, или проектирование устройств квантовой памяти (или квантового гироскопа) на основе движения квантовой частицы (со спином ½ или без спина) в слабом гравитационном поле под воздействием случайных возмущений, рассматривается с позиции описания данных устройств как объектов управления (ОУ).

В обоих случаях ОУ находятся в заданном пространстве-времени с определенной метрикой и геометрией, в гравитационном поле под воздействием внешних случайных сил и должны быть описаны соответствующими математическими моделями, которые содержат надлежащие физические эффекты. Проявление ( не ) учтенных в моделях релятивистских и квантовых эффектов отражается на качестве интеллектуального управления, так как базы знаний интеллектуальных систем управления (ИСУ) проектируются с учетом физической сущности динамического поведения ОУ.

До настоящего времени физическая теория моделей управления находится в стадии своего становления. Период переосмысления принципов системной инженерией и необходимости учета такого рода физических эффектов осуществлен благодаря результатам работ Эйнштейна, Дирака, Фейнмана, Алферова, Манина, Дейча, Шора, Гровера, Прескиля, Самойленко и мн. др. в области разработки основ квантовой инженерии, а также Синга, Котельникова, Уилла, Седова, Эшби, Брумберга, Копейкина и мн. др. в области релятивистской небесной механики и релятивистской навигации КЛА. Необходимость разработки ИТ с учетом квантовых эффектов продиктована также объективной формой (подтвержденная практикой) законов Мура (1965 г.) и Ландауэра (1961 г.), которые показали направление развития микроминиатюризации элементной базы электронных устройств, эволюция которой привела к необходимости учета ограничений в процессах проектирования потерь от тепловых и квантовых флуктуаций, а также физической меры стоимости быстродействия и производительности квантовых вычислительных процессов.

Группой Котельникова проведена большая работа по радиолокации измерения орбитального движения планет Солнечной системы независимо от модели пространственно-временного континуума и показано, что без учета релятивистских поправок в рамках ньютоновой небесной механики промах КЛА при запуске на планеты может достигать от 200 до 500 км.

Разработка логически непротиворечивых и адекватных (корректных) моделей ОУ с целью эффективной реализации интеллектуальных систем управления (ИСУ) новыми видами современной техники является одной из актуальных проблем для современного этапа развития теории и систем управления. Диапазон применения современных ИСУ физическим экспериментом включает в себя, например, от сложных макрообъектов управления типа КЛА до квантовомеханических моделей нанотехнологий (на микро- и наноуровнях) с необходимостью учета релятивистских и квантовых эффектов общей теории относительности и квантовой механики соответственно. Выбор корректной модели, в первую очередь ОУ минимальной алгоритмической сложности, является важной для практики задачей. Однако критерий минимальной алгоритмической сложности при выборе метода описания модели ОУ требует уточнения и физического обоснования. Примером могут служить реальные факты.

Рассмотрим ранее упомянутый пример результатов группы Котельникова. Так при оценке возможных отклонений траекторий движения КЛА (как ОУ в задаче инерциальной навигации), вычисленных по классической теории, от траекторий движения планет Солнечной системы, экспериментально установленных радиолокационными методами, было выявлено следующее обстоятельство. Для гелиоцентрических расстояний планеты Марс отклонение экспериментальных данных составляет 150 км по отношению к расчетным данным, основанным на классических теориях движения планет, и планеты Венера до 500 км, соответственно, и на основе релятивистской теории с ошибкой измерения до 10 м (на протяжении времени наблюдений в 20 лет) 72. Таким образом, модель движения планет с учетом релятивистских эффектов является корректной для навигации КЛА даже в пределах Солнечной системы, несмотря на широко распространенное интуитивное представление о пространственно-временном континууме в классической механике инерциальной навигации КЛА.

Квантовые модели конденсата Бозе-Эйнштейна на основе нелинейной модели уравнения Шредингера (типа уравнения Питаевского–Гросса) для моделирования наноструктур или модели уравнения типа Гинзбурга-Ландау и мн. др. являются важным примером необходимости учета квантовых эффектов в математических моделях ОУ нанотехнологий и т.п. Необходимость учета квантовых эффектов и квантовой логики привело к необходимости развития квантовой _{информатики}73,74,75,76,77,78,7980_.

Системный анализ разработки и проектирования ИСУ для многих моделей такого рода ОУ тесно связан с необходимостью корректного учета существующих физических ограничений. Ограничения на описание динамического поведения сложного физического ОУ (в частности, на предельную точность процессов измерений и управления; выбор модели пространства-времени и др.) накладываются известными физическими законами (из таких дисциплин как статистическая механика, теория относительности, термодинамика, теория информации и квантовая механика). Примером таких ограничений являются следующие: термодинамические ограничения на физическую реализацию математических моделей ОУ; различные типы обобщенных информационных соотношений неопределенности Гейзенберга; квантовые ограничения на пропускную способность передачи информации с учетом термодинамических и квантовых флуктуаций; квантовые оценки предельных возможностей точности измерений параметров ОУ и процессов управления в нанотехнологиях, релятивистские ограничения на скорость передачи данных и мн. др. Данные ограничения должны быть учтены в алгоритме проектирования объективных БЗ в ИСУ.

Повышение требований к точности управления в нанотехнологиях с учетом квантовых эффектов (например, исполнительных устройств – квантовых электромеханических систем) приводит к логическому переходу в квантовую область процессов измерений и управления на атомно-молекулярном уровне. В свою очередь, происходит неизбежный пересмотр физических основ самой теории управления. Аналогичный результат получен при разработке основ квантовой теории информации и квантовых вычислений, приведших к пересмотру аксиоматики моделей физических вычислений и логическому обобщению тезиса Тьюринга-Черча. Многие из перечисленных проблем физической теории и систем управления рассматривались ранее. Были рассмотрены конкретные примеры и получены важные выводы о необходимости учета физической природы самого ОУ в структуре и предельных возможностей процессов управления.

Роль корректной интерпретации физической и математической моделей эксперимента81, взаимосвязь с необходимым уровнем полноты извлекаемых при измерении знаний, алгоритмической сложности математических моделей ОУ и влияние перечисленных факторов на робастность формируемой БЗ в ИСУ (функционирующих в динамически изменяющихся непредвиденных ситуациях управления) в теории управления практически не исследовались.

Принципиальное значение при формировании объективных знаний имеет глобальная оценка функциональной реализуемости аппроксимации моделей при наличии логико-информационных границ и физических (термодинамических, квантово-релятивистских) ограничений на описание реальных нелинейных ОУ. На основе достоверности извлекаемого количества информации определяется информационная оценка приращения риска (статистической корректности) от редукции полноты формируемого описания модели ОУ, и границ её применимости.

В данной работе роль особенностей физических ограничений и информационных границ рассматривается с позиции специфики новой проблемы теорий искусственного интеллекта и процессов интеллектуального управления: возможности формирования объективных баз знаний (БЗ) в процессе проектирования робастных ИСУ путем извлечения знаний и ценной информации из динамического поведения модели самого физического ОУ.

Корректное описание модели ОУ существенно влияет на качество формируемой БЗ и, таким образом, на эффективность применения разрабатываемых структур ИСУ. В частности, в данной книге описаны неклассические логические, квантовые и релятивистские эффекты, влияющие на описание модели ОУ и оптимальное управление динамическими системами. Дана информационная оценка (нижних и верхних) границ риска, возникающего из-за необходимости учета ограниченных возможностей информированности исследователя о свойствах ОУ и влияющего на качество разработки математической модели исследуемой системы.

Приведены термодинамические условия на интерпретацию физической реализуемости (инвариантных к возмущениям) динамических систем управления, на точность аппроксимации модели ОУ и полноту формирования робастных БЗ в ИСУ с глубинным представлением знаний.

Однако прогресс развития и создания подобного рода ИТ сталкивается с трудностью восприятия специалистами по логике интерпретации квантовых и релятивистских эффектов, которые можно использовать для создания технологии проектирования новых видов компьютеров типа квантового компьютера (включая новые виды моделей квантовой релятивистской информатики, квантового программирования, технологий интеллектуальных вычислений таких как квантовые мягкие вычисления, квантовые генетические и иммунные алгоритмы, квантовые нейронные сети, ДНК вычисления и др.) и применять на практике управления сложными ОУ в непредвиденных ситуациях управления. Важным (и необходимым для практики) является методологический аспект: корректность, сложность и точность аппроксимации подробного описания (и доступного для специалистов в области теории и систем управления) физических и математических моделей ОУ на основе релятивистской квантовой механики.

Слабоструктурированная модель ОУ является источником извлечения знаний и используется в интеллектуальных квантовых мягких вычислениях для проектирования моделей робастных ИСУ в непредвиденных ситуациях управления физическим экспериментом. Необходимость данного описания объясняется во многом трудностями восприятия квантовых и релятивистских эффектов, результатов квантовой и релятивистской теории информации и возникающих при физической интерпретации логических «парадоксов», противоречащих выводам классической Булевой логики.

Переход от традиционных методов к новым инновационным образовательным технологиям доступного изложения основ квантовой механики и теории относительности связан также с фактом существования психологического и информационного барьеров восприятия инженерной аудиторией физической модели интерпретации логики событий в теории относительности и математического аппарата квантовой механики, «парадоксов» выводов квантовой и релятивистской логики.

Данный факт отражается непосредственно, например, при изложении решений, получаемых на основе квантовых алгоритмов, или при выводе уравнений движения КЛА и квантовой частицы со спином при воздействии случайных возмущений в искривленном пространстве-времени.

Поэтому для разработки прикладных моделей новых видов интеллектуальных вычислений и их эффективного применения в прикладных задачах управления возникла необходимость формирования новых прорывных образовательных программ с целью более детального и доступного изложения основ квантовой механики, используемых, например, в квантовой информатике на основе теории квантовых вычислений и квантовых алгоритмов.

В частности, в Институте Системного Анализа и Управления Государственного университета «Дубна» совместно с Лабораторией Информационных Технологий и Учебно-Научным Центром Объединенного Института Ядерных Исследований РАН РФ (Дубна, Россия), МГТУ им. Н.Э. Баумана, Институтом Математики и Информатики (Кишинев, Молдова), University of ElectroCommunications ( Tokyo, Japan ) и Università degli Studi di Milano ( Crema, Italy ) особое внимание данному вопросу уделяется при подготовке бакалавров, магистров и инженеров-исследователей в области компьютерных нанотехнологий, информатики, ИСУ и квантовых стратегий принятия решений, робототехники и мехатроники на основе разработанных прорывных образовательных программ.

Здесь отметим только отдельные иллюстративные примеры и особенности роли квантовой информатики в разработке ИТ интеллектуального управления квантовыми и релятивистскими системами [4-12].

Более детально данные вопросы освещены в последующих второй, третьей и четвертой частях данного работы после изложения необходимых сведений из указанных прикладных проблемно – ориентированных областей квантовой релятивистской информатики.

Примечание. Особо подчеркнем, что публикаций (доступных в сети интернет) в области квантовой информатики достаточно много. Поэтому освещаются менее известные в литературе модели и физические эффекты прикладной квантовой информатики, необходимые для разработки корректных компьютерных технологий (computer science technology) и технологий интеллектуального квантового управления (intelligent quantum control technology). Особое внимание уделено вопросам освещения экспериментальных результатов, подтверждающих искомые физические эффекты. Этот факт объясняется бурным развитием данной прикладной области наукоёмких коммерчески привлекательных ИТ и существенным отставанием образовательных программ от освещения современных результатов в области информатики и управления.

Рассмотрим кратко некоторые особенности обсуждаемой проблемы c позиции современной физики, нестандартной (немонотонной) логики суждений и теории систем.

• 5.    Физические ограничения и математические особенности расширения интерпретации проблемы Бэкона

В общем виде моделированием называют процесс воспроизведения и построения модели того или иного явления реального мира, т.е. модель – это абстрактная аппроксимация реального явления , сохраняющая его существенную структуру таким образом, чтобы ее анализ дал возможность определить влияние одних сторон явления на другие или же на явления в целом. При изучении физического, логического, мысленного или другого какого-либо явления на современном этапе первоначально изучаются качественные особенности проблемы посредством имитационного моделирования.

На первом этапе моделирования качественное представление переходит в количественное описание. На втором этапе необходимо решать задачу планирования физического (имитационного) эксперимента и формирования модели исследуемого физического объекта по экспериментальным результатам (большим неструктурированным данным) с последующей оценкой корректности полученной модели.

На рис. 1 приведена обобщенная функциональная структура для поиска решения проблемы Бэкона создания моделей физических объектов и процессов на различных уровнях описания и применения физических законов функционирования.

Таким образом, модель можно определить, как возникает условный образ (упрощенное изображение или аппроксимация) реального объекта (процесса), который создается для более глубокого изучения реальной действительности. Для компенсации возникающих в процессе моделирования и эксперимента аппроксимаций и упрощений требуются новые принципы интеллектуального управления физическим экспериментом и соответствующего инструментария исследования, позволяющие ослабить влияние ошибки аппроксимации на качество модели и сформировать робастные модели физических объектов, не чувствительных к изменениям условий функционирования и внутренним изменениям параметров структуры (В.А. Фок, 1936). В результате возникает проблема разработки модели физического или логического объектов и самого интеллектуального управления робастным физическим и логическим экспериментом с учетом, например, начальной априорной информации и других особенностей объекта82.

Согласно взаимосвязям блоков в структуре на рис. 1, обсудим предварительно, прежде всего, некоторые аспекты процессов измерений в физических экспериментах (в блоке «Измерение и тестирование»), а также роль логической и физической интерпретации полученных результатов измерений.

Трудности поиска решения такой задачи, в свою очередь, связаны с необходимостью реализации ряда физических и информационно-термодинамических принципов робастного интеллектуального управления. К таким принципам в первую очередь относятся: (i) принцип компенсации информационной неполноты описания модели (в общем случае слабоструктурированных) объектов управления (ОУ) выбором соответствующего уровня интеллектуальных вычислений (ИВ); (ii) принцип соответствия алгоритма интеллектуального управления уровню сложности и неполноты представления знаний о внешней среде функционирования ОУ (связь информационной энтропии с мерой алгоритмической сложности Колмогорова); (iii) принцип минимума потерь полезного ресурса (минимум обобщенной энтропии – физический закон оптимального управления) в системе «объект управления + регулятор»; и (iv) принцип не разрушения и повышения эффективности нижнего исполнительского уровня системы управления физическим экспериментом за счет самоорганизации баз знаний (БЗ) интеллектуального регулятора.

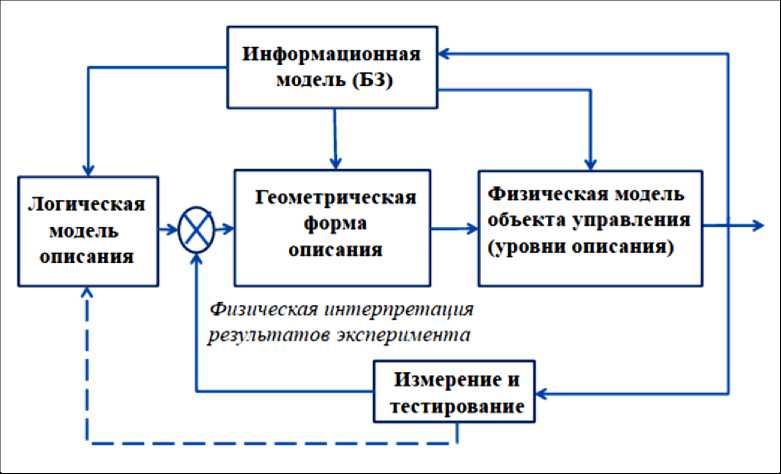
Рис. 1. Функциональная структура создания физических моделей объектов и процессов

Такой подход существенно расширяет проблему Бэкона и ее решение, являясь ее обратной постановкой задачи – построить корректную модель ОУ по ограниченным или, наоборот, большим экспериментальным данным и в условиях недоопреленности структуры ОУ.

Выполнение и реализация новых физических (информационно-термодинамических) принципов интеллектуального робастного управления осуществляются на основе решения следующих трех принципиальных проблем.

• А .    В первом случае, в отличие от прямой задачи (описания знаний количественными характеристиками), рассматривается решение обратной задачи теории искусственного интеллекта: извлечение, обработка и формирование знаний из количественных данных физических и логических экспериментов. В этом случае разработанная технология проектирования объективных БЗ на основе оптимизаторов БЗ на мягких и квантовых вычислениях исключает субъективизм экспертных оценок, обеспечивает достижение требуемого уровня робастности интеллектуальных систем управления (ИСУ).

Б . Во втором случае рассматривается проблема разработки и физического обоснования математической модели квантового алгоритма управления самоорганизацией знаний для формирования робастных БЗ в реальном времени. Важна при этом роль прямых аналогов физических (квантовых и термодинамических) эффектов в реализации процесса гарантированного достижения качества управления на основе технологии квантовых, мягких и дробных вычислений.

При этом основное внимание уделяется описанию и интерпретации качественных особенностей биологически воспроизводимой (биоинспирированной) эволюции самоорганизации, основные компоненты которой описываются квантовыми операторами и составляют физическое содержание разработанной модели квантового алгоритма управления процессом самоорганизации.

В этом случае рассматривается задача робастного управления в непредвиденных ситуациях на основе квантовых стратегий принятия решений в виде программного инструментария квантового нечеткого вывода как частного случая разработанного квантового алгоритма управления самоорганизацией знаний.

• В.    Решение третьей проблемы демонстрирует результаты применения ИТ проектирования робастных БЗ непосредственно в структуре ИСУ. При этом существуют особенности проектирования робастных БЗ для непредвиденных ситуаций управления физическим

4.1.    О принципах построения логически непротиворечивых моделей физических процессов и систем в ИТ

экспериментом и в условиях информационного риска для ИСУ, включающих в свою структуру оптимизаторы БЗ.

Синергизм неточной ( imperfect ) информации и синергетический эффект квантовой самоорганизации БЗ в условиях непредвиденных ситуаций основан на технологии извлечения скрытой в классических состояниях (неизмеримой в общем виде классическими приборами) квантовой информации (дополнительный информационный ресурс).

Рассмотрим поэтому на данном этапе кратко некоторые общие принципы построения моделей.

С позиции системной инженерии, очевидно, что анализ процесса моделирования должен начинаться с восприятия реальности существования моделируемых объектов, т.е. признания объективной реальности. Этот анализ основывается на следующих основных принципах теории отражения когнитивных процессов:

• -    Модель является отражением реально существующего объекта, причем гносеологическим отражением.

• -    Модель является гомоморфным отражением объекта, следствием чего является сокращение и упрощение структуры оригинала. Модель воспроизводит лишь основные, наиболее существенные для исследования стороны изучаемого объекта. (Напомним, что Гомоморфизм – когда несколько свойств объекта отображаются в одно свойство; Изоморфизм – взаимно однозначное соответствие (одно в одно)).

• -    Модель предполагает участие в ее создании и конструировании познающего её субъекта исследования.

4.2.    Физическая реальность и принципы моделирования физических объектов

В зависимости от логических свойств и связей моделей физических явлений разрабатываемые в системной инженерии модели можно разделить на три типа: физические, расчетные и математические модели. Здесь кратко отметим особенности математических моделей.

Особенности математических моделей физических явлений состоят в том, что они точны, абстрактны и передают информацию (логически однозначным) образом. По сравнению с лабораторным (натурным) экспериментом компьютерный эксперимент дешевле, безопасней, может проводиться в тех случаях, когда натурный эксперимент принципиально невозможен.

Математические модели , являясь наиболее общими и абстрактными, используя символы математического или логического характера, служат отражению и анализу некоторых свойств физических объектов и явлений. Особые трудности возникают при решении задач с большой размерностью, расплывчатой (нечеткой) постановкой, неопределенностью информации и т.д.

В постановке таких задач появляются неклассические понятия и моменты, такие, как плохая формализуемость, нестандартность, противоречивость, некорректность; часто приходится отказываться от привычных определений и понятий. Следует отметить, что в теоретической физике⁸³ данному вопросу давно уделяется пристальное внимание: «Таким образом, обобщение физических теорий связано не только с приобретением новых понятий, но и с отказом от старых. Здесь необходимо отметить следующий психологический фактор: отказ от старых, привычных физических понятий дается несравненно труднее, чем усвоение новых понятий, не связанных с таким отказом .

Чтобы ясно представить себе необходимость такого рода отказа, мы попытаемся проследить процесс образования понятий в направлении, в известном смысле обратном историческому развитию теории. Если идти в этом направлении, то мы должны будем исходить из наиболее общей известной в данный момент физической теории; мы убедимся, что при каждом ее упрощении, при каждом переходе к более частной теории будут возникать все новые и новые физические понятия. Но тогда будет ясно, что обратный процесс – переход от более частной теории к более общей – должен быть связан с отказом от некоторых физических понятий».

Рассмотрим теперь кратко особенности принципов моделирования физических объектов и их логическую взаимосвязь.

Применительно к исследованию физических явлений создание качественной модели – это формулировка физических закономерностей явления или процесса на основании данных эксперимента.

Считается, что практика есть критерий истинности теории . Однако наблюдения, строго говоря, не могут доказать справедливость теории. Они могут лишь косвенно свидетельствовать о её справедливости или опровергнуть ее. Субъективный анализ наблюдений может фальсифицировать теорию, поэтому важную роль играет принцип воспроизведения (повторяемости) экспериментальных физических результатов при корректном воспроизведении экспериментальных условий вне зависимости от места и времени .

Формализация экспериментального статистически достоверного материала – не единственный способ построения математической модели. Важную роль играет принцип получения моделей, описывающих частные объекты, из моделей более общих .

Основной принцип построения корректной математической модели физического явления

При построении математической модели изучаемого объекта, из всех характеризующих его связей выделяются наиболее существенные. Если в системе действует несколько факторов одного порядка, то все они должны быть учтены, или отброшены одновременно.

Одним из главных принципов моделирования является следующий принцип:

модель должна соответствовать оригиналу только в главном, существенном, в том, что интересует исследователя; все несущественное должно быть отброшено.

Достаточно привести цитату из упомянутой работы В.А. Фока (см. сноску 74) в следующем виде: «Как мы уже говорили, уравнения теоретической физики никогда не бывают абсолютно точными. Даже и та теория, которая на данном этапе развития физики является наиболее общей, не может претендовать на универсальность, так как она содержит в себе ряд физических пренебрежений. Поэтому, приступая к формулировке такой теории, необходимо, прежде всего, выяснить, каковы эти пренебрежения и чем ограничена применимость тех основных физических понятий, с которыми данная теория оперирует. Одной из наиболее общих существующих физических теорий является квантовая электродинамика. Теория эта не входит в рассмотрение природы атомной структуры материи, а принимает ее как экспериментальный факт. Структура материальных частиц в ней не рассматривается, а эти частицы характеризуются суммарно некоторыми константами, в частности их зарядом и массой.

Такого рода не строгости, которые являются следствием лежащих в основе теории пренебрежений, несомненно, являются крупным ее недостатком. Тем не менее, в данной приближенной теории эти не строгости физически необходимы. Они представляют по существу грубый прием, посредством которого исправляются недостатки первоначальной формулировки, неправильно учитывающей, например, роль световых квантов с весьма большой энергией.

Тем не менее, несмотря на все свои недостатки, теория, основанная на волновом уравнении, правильно описывает весьма обширный класс физических явлений. Она с большой степенью точности передает процессы излучения атомов и молекул, и позволяет определить не только частоты, но и естественную ширину спектральных линий. Она приводит к правильной формуле для рассеяния света свободными электронами (формула Клейна-Нишины).

Наконец, она дает поправки к кулоновскому закону взаимодействия между электронами; поправки эти происходят от испускания и поглощения электронами световых квантов (в классической теории соответствующая поправка толковалась как учет запаздывания потенциалов)».

Можно отметить ещё несколько принципов моделирования физических явлений:

• -    Принцип аналогий: одним из плодотворных подходов к моделированию сложных физических объектов является использование аналогий с уже изученными явлениями;

• -    Принцип иерархичности моделей: принцип «от простого к сложному» – построение цепочки (иерархии) все более полных физических моделей, каждая их которых обобщает предыдущую, включая её в качестве составного случая;

• -    Принцип универсальности: если закон сохранения справедлив для произвольного n -мерного объема, то он справедлив и для любой его части;

• -    Принцип логической непротиворечивости моделей: для построения математических моделей естествознания необходимы четкие непротиворечивые формулировки основных понятий, которые будут положены в основу самих исследований.

4.3.    О корректности физических моделей и логической непротиворечивости математических моделей

Рассмотренный традиционный подход (и многие другие методы) к решению задач теории и практики разработки моделей физических и логических объектов и процессов на основе существующих в прикладной математике формально-логических методов ставит своей целью создание точных (в широком смысле) моделей на основе применения инструментария строгих суждений или логических выводов принятия решений. В частности, в теории систем управления физическими экспериментами основное внимание приходится уделять вопросам оценки корректности, полноты, непротиворечивости, замкнутости, устойчивости, управляемости и многим другим качественным аспектам описания слабоструктурированных сложных моделей физических объектов и процессов управления84.

Вопрос истинности утверждений и высказывания типа « математическая модель адекватна реальному физическому объекту » оставался по существу открытым и не мог быть решен только в рамках принятого метода исследования [4].

При применении в прикладных задачах обработки больших массивов данных физических экспериментов традиционными методами исчислений по конечному количественному результату численного алгоритма осуществляется соответствующая оценка качественного свойства исследуемого объекта (например, определение глобального экстремума сложной функции от многих аргументов). Логическая оценка свойства в общем случае может быть осуществлена только в конце количественных вычислений, а для алгоритмически неразрешимых численных проблем (в виде энтропийных мер сложности алгоритма по Колмогорову), часто искомая оценка не может быть достигнута [5-7].

Математическая модель (созданная на знаниях или данных из процессов обучения, на основе физических или логических законов, на извлеченных данных из физических измерений или наблюдений и т.д.) является неполной в силу принципиальной недоказуемости ее полноты в рамках принятой аксиоматики физической интерпретации [4, 7, 8].

В свою очередь, корректная физическая интерпретация делает математическую модель объекта реализуемой85. Полнота и адекватность модели интерпретируется как выполнение принятых за основу построения модели исходных аксиом и физических ограничений в виде законов поведения физической модели86.

Примечание. Здесь имеет место аналогия с теоремой Геделя о неполноте истинных формул арифметики [9, 10], информационные аспекты которой рассмотрены в [11]. Построение физически и математически корректных моделей динамических систем, например, в процессах управления физическим экспериментом представляет одну из основных и сложных задач теории автоматического управления [4, 12-15]. Основное содержание данной проблемы состоит в решении следующих проблем: описание процессов, происходящих в объектах управления, соответствующих методов формализации и установления соответствия (адекватности) получаемых таким образом моделей с исходным объектом, а также с методами исследования (в зависимости от уровня физической строгости и математической корректности87). Следует отметить, что процесс построения носит сложный эволюционный характер88, связан с неизбежной аппроксимацией реального объекта89 и приводит к потере информации при его описании90. При этом гипотезы и аксиомы, по которым осуществляется аппроксимация и описание реального объекта с помощью соответствующей модели, могут учитывать не все смысловое содержание реальной сущности физического процесса [4, 7], что приводит к дополнительному приращению информационного риска и неопределенности в описании модели объекта управления (ОУ) [12, 15, 16]. Таким образом, сложность математического описания физических систем как моделей ОУ приводит к необходимости аппроксимации и применению приближенных решений, которые не гарантируют в общем случае необходимые и достаточные условия достижения цели управления в непредвиденных ситуациях и пределы информационного риска [4, 15].

Принципиальное значение при формировании моделей ОУ имеет глобальная оценка функциональной реализуемости аппроксимации при наличии логико-информационных границ и физических (термодинамических, квантово-релятивистских и др.) ограничений на описание реальных нелинейных ОУ. На основе достоверности извлекаемого количества информации определяется информационная оценка приращения риска (статистической корректности) формируемого описания модели ОУ, и границ её применимости91.

Примечание . В системном анализе хорошо известен факт, что в общем виде модель является приближением (с неизвестной, в общем случае, ошибкой аппроксимации) физического (реального) конечного ОУ. Менее известно, как оценить точность применяемого способа аппроксимации, и ещё меньше – как доказать корректность (например, по несколько заданным и часто плохо определенным критериям) и полноту разработанной модели (в смысле информативности представления описания свойств заданного физического ОУ для достижения цели управления).

Ошибка аппроксимации может иметь различной природы характер: 1) ошибки численного интегрирования дифференциального уравнения, описывающего движение нелинейного ОУ; 2) геометрического характера в виде некорректного выбора модели пространства – времени, например Евклидова пространства вместо пространства Римана, Лобачевского или Финслера; 3) физического характера в виде выбора модели описания ОУ на макроуровне вместо рассмотрения модели ОУ на микроуровне; 4) логического характера в виде выбора модели интерпретации результатов физического (или мысленного) эксперимента в рамках Булевой логики, вместо применения методов квантовой или релятивистских логик, например, для интерпретации нелокальных свойств явления телепортация или парадокса Эйнштейна-Розена-Подольского (ЭПР); 5) ошибка измерений параметров модели; 6) пренебрежением малыми параметрами с целью упрощения описания модели, и мн. др.

Одной из целей данной работы, является описание существующих объективных (физических, информационных и логических) ограничений, которые необходимо учитывать при разработке корректных физических и математических моделей ОУ и включать в содержание соответствующих БЗ в структурах ИСУ физическим экспериментом со слабо структурированными объектами.

Например, динамическое поведение ОУ и системы управления (регулятора) служит источником объективных знаний для формирования баз знаний (БЗ), полнота (soundness) которой зависит от достоверности извлекаемой из конкретного источника информации. Неточность (imperfect) измерения (обусловленная объективной природой объекта) и недостоверность (unreliable) представления извлекаемой информации (например, неполнота предоставления знаний экспертом или из-за присутствия человеческого фактора в контуре управления) приводит к повышению информационного риска и возникновению непредвиденных ситуаций управления, компенсация которых для обеспечения робастности управления осуществляется применением необходимого уровня интеллектуальных вычислений (ИВ). Рассматриваются возможные подходы к построению аппроксимаций и оценок робастности таких моделей, роли видов ИВ в компенсации неточностей описания моделей ОУ и смежных вопросов, таких как синергизм информации при разработке процессов самоорганизации информационных процессов в ИСУ и др.

Предварительно опишем понятие физической и математической корректности описания ОУ на основе определений физической, математической и расчетной модели ОУ.

• 5. Особенности логики взаимосвязей физических и математических робастных моделей физических объектов в теории систем

5.1.    Физически строгие и математически корректные модели объектов и процессов

Термин «модель», подобно термину «устойчивость», несет большую смысловую нагрузку. Как правило, в него вкладывается различное содержание. При этом возникают существенные противоречия в определении таких понятий как «физическая», «расчетная» и «математическая» модель. Необходимо отметить, что проблема создания моделей имеет фундаментальное значение не только в кибернетике, как науке о системах, но и для всех естественных и технических наук.

Ниже формулируются (по возможности развернутые) определения употребляемых в этой области понятий, которые иллюстрируются рядом конкретных примеров.

Под физической моделью какого-либо процесса, например, процесса работы системы при внешнем возмущении следует понимать по возможности полное (в соответствии с достигнутым уровнем знаний) описание этого процесса в физически содержательных терминах. В физическую модель должны входить без всяких упрощений все известные функциональные, дифференциальные и другие соотношения и связи между структурными элементами процесса. Физическая модель должна также содержать имеющиеся экспериментальные данные, относящиеся к рассматриваемому процессу, изложение гипотез, которые могут быть сформулированы по поводу еще не изученных связей и соотношений между элементами системы. Другими словами, физическая модель представляет собой содержательное отражение реальных явлений или процессов на уровне современных знаний.

Физическая модель не может быть создана путем чисто эмпирического наблюдения данного класса объектов или процессов. Разумеется, для создания любой физической модели (которая может рассматриваться как физическая теория) необходимы эксперименты и наблюдения, однако понимание (корректная интерпретация) самих экспериментов невозможно без теории, т.е. без наличия физической модели изучаемого класса объектов и процессов. Набор эмпирических суждений и соотношений носит довольно запутанный характер, в котором существенные стороны изучаемых объектов и процессов нередко тонут в массе случайных или несущественных факторов. Построение подлинной физической модели или физической теории означает сведение множества эмпирических данных к немногим фундаментальным положениям и принципам, в которых отражалось бы существо изучаемых процессов. Построение подобной физической модели требует часто новых идей и понятий, нередко противоречащих уже сложившим представлениям.

Пример . Если через R обозначить реальный класс изучаемых объектов и процессов, через S – набор эмпирических данных о них и известных к этому времени теоретических представлений в данной области и, наконец, через Φ – физическую модель (или теорию) этого класса объектов или процессов, то можно написать следующее соотношение: R → S → Φ .

Замечание . По поводу связи между R , S и Φ Альберт Эйнштейн⁹² в письме к Б. Соловину замечает, что психологически Φ покоится на S , но, если речь идет о дальнейшем развитии физической теории, то не существует никакой формальной логической дороги, ведущей от S к Φ , но лишь интуитивная (экстралогическая) связь между ними. Та же мысль развивается Эйнштейном в письме к известному французскому математику Жаку Адамару. В другом месте Эйнштейн замечает, что «подлинной ценностью является, в сущности, только интуиция»⁵⁴.

В связи с отмеченным, рассмотрим некоторые проблемы, решение которых влияет на качество создаваемых моделей по результатам физических экспериментов и установления адекватности моделей.

Проблема : Выявление противоречивости, парадоксов и корректности формальной физической модели Φ на основе логики интерпретации эмпирических данных измерений S

В качестве примера физической модели Φ можно указать на квантовую модель строения атома Нильса Бора, развитую в последующих работах Гейзенберга и Шредингера. Рассматриваемая модель к моменту ее появления не только логически не следовала из известных к тому времени результатов спектроскопии и классической электродинамики, т.е. из совокупности знаний, которые обозначались ранее как S , но даже резко противоречила им.

Тем не менее, эта модель не только объяснила происхождение уже известных спектральных частот различных атомов, но позволила предсказать новые, неизвестные ранее спектральные частоты в низко и высоко частотной областях. Эта модель послужила основанием для создания современной физики – квантовой теории. Противоречие между классической электродинамикой и квантовой теорией привело к необходимости перестройки самой классической теории электродинамики. Так возникла квантовая электродинамика.

Следует особо подчеркнуть, что, оставаясь на классической точке зрения, следовало бы предположить, что внутри каждого атома есть система классических радиостанций, излучающих частоты, наблюдаемые при помощи спектроскопов. Поэтому невозможно было формально логическим путем построить модель атома Бора на основании данных спектроскопии.

Таким образом, между S и Φ действительно не существовало никакой формальной логической связи. Возникновение Φ (гипотеза Бора) привело к необходимости изменения самого комплекса S , поскольку предложенная модель Φ противоречила комплексу S . При этом часто само изменение S осуществлялось на основе интуиции исследователя.

Примечание . В связи с этим поясним некоторые важные методологические и логические аспекты проблемы выявления адекватности эмпирических данных измерений S и логики оценки непротиворечивости формальных физических теорий моделей Φ . Конечно, процесс построения физической теории и соответствующей формальной логической модели по своей природе не является чисто дедуктивным процессом и не может быть полностью формализован. Однако разработанная теория и построенная на ее основе модель физического объекта (даже слабоструктурированная) основана на дедукции, в той или степени формализованной. Поэтому построение логических систем, отличных от классической логики и учитывающих возможности и особенности, не учтенных в классической логике, способных выявлять логические противоречия в формальных теориях и системах, является важной задачей.

Особенно остро данная проблема имеет место при анализе противоречий логических (мысленных) экспериментов, которые являются неотъемлемой частью при разработке физических теорий, планировании физических экспериментов и корректной интерпретации полученных результатов. Постановка задачи о выявлении противоречий требует построения логики, с помощью которой могут быть рассмотрены противоречивые теории, немыслимые в рамках классической теории. Общая проблема построения противоречивых формальных теорий и лежащей в их основе логики была в явном виде сформулирована в 1948г. С. Яськовским93. Было построено логическое исчисление, в котором из противоречия не всегда следует «все, что угодно».

Логические исчисления, которые могут лечь в основу противоречивых формальных теорий, получили наименование «паранепротиворечивых» (paraconsistent logic)94.

Примечание . Отметим, что формальную систему называют противоречивой , если ее теоремами или аксиомами являются какие-либо две формулы А и не – А ( A ), одна из которой есть отрицание другой. Систему называют тривиальной , если любая (правильно построенная) формула является ее теоремой или аксиомой. Любая нетривиальная система, основанная на классической логике, является тривиализуемой, так как присоединение к ней в качестве аксиом двух формул, одна из которых есть отрицание другой, превращает эту систему в тривиальную.

Пример . В качестве примера нетривиализуемой системы можно привести импликативное пропозициональное исчисление, единственной логической связкой которого является импликация⁹⁵. «Промежуточное положение» занимает так называемое минимальное исчисление, в котором из противоречия следует не любая формула, а лишь отрицание любой формулы. Все главные дедуктивные средства в логике противоречивых систем должны быть сохранены в максимально возможной степени, так как эти средства являются основой всех обычных рассуждений. В частности, должна быть сохранена позитивная логика, т. е., логические законы, не связанные с отрицанием. Фрагмент классической логики называется максимальным , если добавление к нему недоказуемой в нем формулы в качестве схем аксиом, либо дополняет его до классической логики, либо делает его тривиальным. Таким образом, речь идет о построении максимального фрагмента классической логики, не содержащего принципа «из противоречия следует все, что угодно». Такие логические исчисления могут содержать характерные черты, в рамках которых возможны доказательства противоречивости. Действующий в классической логике принцип «из противоречия следует все, что угодно» тесно связан с невыполнением другого принципа, который называется «принципом недоказуемости из посторонних соображений». В обсуждаемой логике противоречивых систем доказуемость (выводимость) А означает «неложность» А , доказуемость не – А – «неистинность» А , а противоречивость А означает «неложность» и «неистинность» А одновременно. Поэтому семантика такой логики подразумевает три истинностных значения – «истина», «ложь» и «противоречие». Причем выделенными являются два из них – «истина» и «противоречие»: наличие доказательства формулы А не означает, что А истинно, а исключает лишь, что А принимает значение «ложь».

Следовательно, получая возможность работать с противоречиями и доказывать противоречивость, логика должна нарушить непосредственную связь между доказуемостью и истинностью. Отказ от принципа «из противоречия следует все» влечет за собой невозможность выразить отличие «истинности» от «не ложности» и «ложности» от «неистинности» средствами самой формальной системы. Различение между этими понятиями может быть проведено на уровне метаязыка. Третье истинностное значение – «противоречие» – может быть содержательно истолковано как «бессмыслица». Оба эти понятия тесно связаны. Бессмыслица может быть охарактеризована как неистинное высказывание, отрицание которого тоже неистинно, и одновременно как неложное высказывание, отрицание которого не ложно. Если высказывание А бессмысленно, то и А , и его отрицание не-А естественно признать неистинными и одновременно неложными высказываниями. Поэтому логика противоречивых систем связана с логическими исчислениями, рассматривающими, наряду с осмысленными, также и бессмысленные высказывания.

Таким образом, путем ослабления классической логики может быть построено исчисление, которое робастно не только к противоречиям, но с помощью которого эти противоречия могут быть выявлены (доказаны). Но ослабление классической логики влечет ослабление связи между доказуемостью и истинностью: доказуемость уже не означает истинность, а для различения между «истиной» и «не ложью» необходим выход на уровень метаязыка. Противоречивость в выразительных средствах языка в математике с одной стороны недопустима, а с другой стороны в любом реальном (в том числе в математическом) языке имеются средства для обозначения объектов, предположение о существовании которых приводит к противоречию и высказывания, о которых являются противоречивыми и бессмысленными.

Поэтому используется терминология, в которой каждое формально правильно построенное слово рассматривается как имя некоторого объекта, а затем выясняется, существует ли названный объект (т.е. имеет ли данное имя денотат). Высказывания о «несуществующих объектах» с точки зрения математической логики не истинны и не ложны – они противоречивы и бессмысленны. При этом объект характеризуется как «не существующий, если предположение о его существовании приводит к противоречию.

Однако понятия «существование» и «не существование» в общем случае носят относительный характер: то, что «не существует» в одной системе представлений, может «существовать» в другой (например, утверждение «треугольник, сумма углов которого не равна П » не существует в евклидовой геометрии, но существует в неевклидовой).

5.2.    Принцип логической и физической непротиворечивости вложения моделей физических процессов

Рассмотрим еще один поучительный пример о связи принципа вложения моделей физических объектов и аппроксимации и выбора расчетной модели физического объекта.

Пример . Рассмотрим физический объект Ф в виде механической системы, показанной на рис. 2 с необходимыми обозначениями.

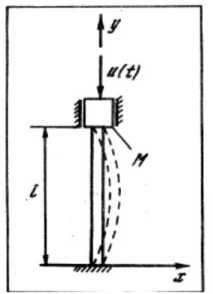
Рис. 2. Модель стержневой системы

Предположим, что экспериментатор наблюдает только поперечные колебания x ( t ) стержня под действием осевой нагрузки U ( t ) . В этом случае уравнение «вход - выход» имеет вид⁹⁶:

x + 2 в + ^ ² ( 1 - 2 ^ U ( t ) ) x + e F ( x, x , x ) = 0,                  (2)

где P,^^, Ц,8 - некоторые постоянные, и да eF(x,x,x) = 2e0xx2 + x(x2 + xx)x + ^yx2n+1, Yn = const.       (3)

n = 1

Если же экспериментатор будет измерять поперечные и продольные колебания стержня, то при соответствующих предположениях уравнения «вход – выход» принимают вид:

x + 2 Д x + ( У ² ( 1 - ky ) x = 0

n²                1

y ⁺ 2 ^e 2 y ⁺ ^ пр y ⁺ ^-[ ^{xx + x} ] = —^U ( t )

.

Здесь А , Р^ п , ^ пр , k – некоторые постоянные величины, характеризующие затухание, частоту свободных колебаний в поперечном и продольном направлениях, к = (б У _пр) соответственно. Таким образом, в этом примере система (2) имеет одну степень свободы, U ( t ) -вход; переменная X ( t ) - выход, у ( t ) - скрытый выход (недоопределенная не наблюдаемая (скрытая визуально) переменная, для которой требуется дополнительное измерение). При этом в модели (4) переменные X ( t ) и у ( t ) взаимозаменяемы в смысле терминологии, а учет скрытого выхода y ( t ) приводит к новой расчетной модели.

Так система (2) относится к классу систем с параметрическим возбуждением, вход U ( t ) описывает параметрические возмущения и относится к классу внутренних входов (последние часто называют внутренними шумами); в модели (4) U ( t ) переходит из класса внутренних входов в класс внешних возмущений, а сама модель имеет в отличие от (2) две степени свободы и содержит существенно нелинейные перекрестные связи, которые могут вызывать новое качественное явление перекачки энергии с одной степени свободы на другую. На этой же модели можно проследить влияние скрытых «малых» членов на качественные особенности динамического поведения системы (3).

Данный пример отчетливо показывает роль создания последовательности моделей – гипотез м г = { m г , м _г²,..., м ; } и тестирования их вложений:

M o f M i } ; M i с M i ^{+ 1}: lim M i = M .

i ^^

Так нетрудно проверить, что модель M 2 из уравнения (4) при у = 0 : M 2 О M ^ , т.е. модель (2) вложена в модель (4).

Действительно, умножая левую и правую части второго уравнения (4) на координату x и складывая с первым уравнением, после всех алгебраических преобразований получим модель (1).

Приведенный анализ основных соотношений имеет в данном случае непосредственное отношение к постулированию связей с заданным физическим объектом Ф и дает, следовательно, содержательную интерпретацию каждого выхода моделей M ^ и M 2 , т.е. данные модели физически реализуемы.

5.3.    Взаимосвязь и непротиворечивость расширенной проблемы Бэкона с принципом вложения физических моделей объектов

Отметим некоторые методологические особенности рассмотренного примера и его связь с проблемой Бэкона.

При разработке моделей (2) и (4) объекта вводились разные гипотезы о физической природе исследуемого объекта ( физическая модель). Так в модели (1) пренебрегалось сжатием стержня от вертикальной нагрузки (продольные колебания стержня) и поэтому расчетная модель имела одну степень свободы, описывающая только поперечные колебания стержня, а математическая модель (1) описывалась дифференциальным уравнением второго порядка. В физической модели (4) учитывались продольные колебания, расчетная модель имеет две степени свободы, математическая модель описывается системой из двух взаимосвязанных дифференциальных уравнений второго порядка. Поэтому вопрос об адекватности физической модели реальному объекту с точки зрения проблемы Бэкона решается выбором и обоснованием гипотез о физической сущности объекта путем моделирования и экспериментальной проверки влияния продольных колебаний (скрытого параметра) на динамику всей системы.

Примечание . Рассмотренное явление влияния и взаимосвязи продольных и поперечных колебаний имеет важное значение при устранении опасного явления «флаттера» или механического резонанса в области аэродинамики и аэроупругости конструкций, в частности к изменению подходов к проектированию всех больше пролётных мостов в мире. Так был разрушен Такомский мост, или мост Такома-Нэрроуз (англ. Tacoma Narrows Bridge ) – висячий мост в США, в штате Вашингтон, построенный через пролив Такома-Нэрроуз (часть залива Пьюджет-Саунд) . Во многих учебниках причиной аварии называется явление вынужденного механического резонанса, когда внешняя частота изменения ветрового потока совпадает с внутренней частотой колебаний конструкций моста. Однако истинной причиной стал аэроупругий флаттер (динамические крутильные колебания) из-за недоучета ветровых нагрузок при проектировании сооружения. Данное явление вызвано «перекачкой» энергии с одной степени свободы на другую, при которой колебания затухают на одной степени свободы и вызывают колебания на другой степени свободы⁹⁷. Другим примером служит, например, танцующий мост в Волгограде⁹⁸.

Таким образом, пренебрежение рядом гипотез (уровень не знания физической природы исследуемого объекта) в физической модели о поведении реального объекта приводит к ее неадекватности и, в ряде случаев, к катастрофическим последствиям.

Отметим также еще одну особенность рассмотренного примера.

5.4.    Проблема логических «парадоксов», адекватности и аппроксимации физической модели и связь с проблемой Бэкона

Рассмотренные физические модели объекта на рис. 2 относятся к проблеме установления адекватности физической модели реальному объекту и математической модели физической модели.

Если рассматривать влияние малых членов в математической модели (2) или (4) на динамическое поведение исследуемого объекта при моделировании, то данная ситуация относится к оценке влияния аппроксимации на качество математической модели и не имеет отношения к оценке адекватности моделей [37]. В этом состоит сущность ошибок и неточностей в содержательной интерпретации моделей многих начинающих исследователей, например⁹⁹.

Исследование адекватности и разработка физически непротиворечивых корректных и математически строгих моделей термодинамических, квантовых и релятивистских объектов, используемых при проектировании квантовых сквозных технологий в рамках проблемы Бэкона [38], требуют более сложных мысленных экспериментов с привлечением технологий виртуальной и дополненной реальности. Достаточно напомнить о трудностях представления пространственновременного континуума 4-мерного мира или состояния квантовой суперпозиции типа «кот Шрёдингера». Конструирование логически противоречивых (с точки зрения Булевой логики) или несуществующих (мысленных) объектов приводит к логическим парадоксам [17-37].

Парадоксы рассматриваются как логические противоречия, в результате «вынужденно» принимаемых предположений о существовании «не существующих» объектов. Данный вопрос имеет важное значение при разработке наукоёмких ИТ типа квантовая релятивистская информатика [38], нестандартных логик образовательных процессов и рассмотрен в Части 2 данной работы.

Вопросы адекватности и аппроксимации физических и математических моделей различных макро- микро- и нано-уровней сложности составляют расширение проблемы Бэкона и рассмотрены в последующих частях данной работы. Перечисленные и мн. др. парадоксы уже эффективно используются в наукоёмких информационных технологиях и требуется дополнительная (нестандартная) логика организации образовательного и учебного процессов.

Выводы

В данной Части 1 общей работы рассмотрены следующие вопросы:

• -    Обсуждаются вопросы организации образовательного и учебного процессов в области наукоёмких информационных технологий и аналитики больших данных на примере квантовой релятивистской информатики.

• -    Построенные на новых знаниях о физических и логических принципах сквозные информационные технологии требуют привлечения дополнительных ресурсов знаний из областей, ранее не используемых или слабо привлекаемых в образовательных программах.

• -    Разъяснена важная роль учета при построении моделей физических, информационных и логических ограничений на вычислительные процессы, процессы обработки и передачи информации при построении физически строгих и математически корректных моделей информационных технологий и взаимосвязь с расширенной проблемой Бэкона познания физических и логических явлений и парадоксов.

• -    Информационно-термодинамические принципы построения вычислительных процессов и процессов сбора, обработки, передачи, хранения и предоставления информации как платформы для аналитики больших данных позволяют дать объективные оценки предельных возможностей используемой информационной технологии и определить пути смены программно-алгоритмической платформы для достижения поставленной цели в рамках решения расширенной проблемы Бэкона.