Нестатистические подходы к анализу состояний технологических систем

Для исследования сложных систем в течение последних десятилетий разработаны новые методы. Они обогатили современную нелинейную теорию динамических систем, крупным достижением которой является открытие превалирования неустойчивостей. Это означает, что возникшие малые изменения параметров системы имеют тенденцию самопроизвольно усиливаться [1], приводя систему к потере устойчивости, т.е. к внезапному переходу в другой режим. Потенциальные предпосылки такого эффекта связаны с существованием притягивающего множества установившихся режимов движения системы в фазовом пространстве. Такие режимы получили название аттракторов (от англ. attract - притягивать) [1,2]. Существование аттракторов систем и процессов было установлено в самом начале 60-годов ХХ-го века. Позднее были выявлены аттракторы трех типов: состояние равновесия, состояние периодического движения и так называемый странный аттрактор, который вскоре стали связывать с проблемой хаотического движения. При переходе системы в состояние, называемое странным аттрактором, параметры системы начинают претерпевать сложные непериодические изменения, в то время как их усредненные значения могут оказаться устойчивыми и практически не зависящими от начальных условий. Построенная в начале 70-х годов ХХ-го века теория катастроф [2], позволила понять, что корректный ответ на вопрос об устойчивости системы возможен лишь тогда, когда установлен факт существования и тип аттрактора. В связи с этим поиск методов его распознавания быстро стал задачей, имеющей первостепенное значение для оценки поведения сложных систем, к которым, естественно, относятся и технологические.

Исследованиями последних лет в области теории устойчивости установлено, что свойства аттракторов у реальных систем нередко отличаются от свойств любого из трех указанных выше «стандартных» типов. Это заметно усложняет задачу анализа устойчивости технологических систем. И все же взгляд на поведение систем с привлечением понятия «аттрактор» раздвигает грани представлений о возможных ее реакциях на изменения определяющих параметров.

Главной характеристикой аттрактора является размерность. Под размерностью аттрактора понимается размерность того фазового пространства, в котором он существует. Оценка размерности аттрактора имеет важное, а порой и принципиальное значение. Пусть, например, набор параметров X1, X2, X3, X4, X5 описывает некоторую технологическую систему. Предположим, что удалось установить размерность аттрактора, оказавшуюся равной 3. На основании этого можно заключить, что лишь 3 из 5 параметров определяют качества системы с позиций устойчивости. Если же в фазовом пространстве пяти параметров системы аттрактор обнаружить не удалось, а по другим критериям система проявляет устойчивость, то есть основания предположить, что исходный набор из пяти параметров системы не является полным и существуют, кроме этих, еще и другие параметры, отражающие способность системы к устойчивому поведению в условиях, в которых она оказывается при функционировании. Отсюда следует, что анализ системы на устойчивость может раскрыть не лежащие на поверхности явлений особенности связей ее параметров, а также выяснить сколько из них «отвечают» за устойчивость системы и при каких сочетаниях их значений система обнаруживает это важное качество.

Во многих случаях анализ аттракторов технологической системы можно осуществлять по фазовому портрету, построение которого связано с математическим ее описанием. Однако, безусловно, наибольший интерес с позиций приложений вызывают безмодельные способы идентификации аттракторов. Основная их идея представлена ниже. Здесь же, следуя [1] и в привязке к трикотажному производству, изложим одно важное в принципиальном отношении соображение, открывающее путь к ее алгоритмической реализации.

Слежение за технологической системой в традиционном представлении есть не что иное, как наблюдение за некоторой совокупностью ee параметров. Однако оно может проводиться путем регистрации во времени и одного какого-либо параметра. На первый взгляд, существуют основания для сомнений в достаточном уровне информативности временнóй последовательности значений единственного параметра, т.к. технологические системы – многопараметрические. Однако, если выбрать параметр, являющийся функцией комплекса факторов, определяющих динамику технологической системы, то оценка ее по одномерной временной последовательности значений такого параметра уже не выглядит чрезмерно упрощенной. Более того, с организационной и технической сторон наблюдение за одним параметром предпочтительнее. При «одномерном» взгляде на систему чрезвычайно важен выбор параметра. Например, если в качестве наблюдаемого параметра использовать поверхностную плотность трикотажного полотна, то по ней нельзя в достаточной мере судить о течении производственного процесса ввиду того, что этот параметр характеризует лишь выпускаемый продукт. Совсем иное по степени полноты представление о производственном процессе возникает при оценке, например, величины отходов при вязании в единицу времени, которая характеризует и технологическую надежность нити, и техническое состояние оборудования, и уровень квалификации обслуживающего персонала, т.к. отходы при вязании содержат следы всех факторов, определяющих состояние данной технологической системы. Кроме того, как показано в работе [1], информативность одномерного временного ряда определяется не только тем, в какой мере в значениях выбранного параметра отражается действие факторов, определяющих динамику системы, но еще и тем, как распорядиться элементами этого ряда. Опишем представленный в [1] способ обнаружения аттрактора и оценки его размерности по последовательности значений единственного параметра системы.

Пусть X0(t) – полученная тем или иным путем временнáя последовательность из N значений параметра системы. Образуем из X0(t) М равновеликих наборов X[u] (u=0,1,2, ... ,[M-1]), каждый из которых состоит из n выбранных подряд ее элементов. При этом любой набор, начиная со второго, формируется после сдвига вдоль последовательности X0(t) относительно пре-дыдущего набора всякий раз на постоянную величину S, принимаемую не меньшей интервала корреляции в исходной последовательности X0(t). По завершении М сдвигов имеем ряд наборов X0, X1,... Xм-1. Элементы каждого набора будем рассматривать как координаты фазовой точки, определяющие ее положение в n-мерном фазовом пространстве. Совокупность таких точек образует фазовый портрет, на котором становится видимым притягивающее множество состояний системы, т.е. аттрактор, если он существует в построенном фазовом пространстве выбранной размерности. При этом аттрактор обнаруживается в виде одной или нескольких областей сгущений фазовых точек на фоне прилегающих зон. Так как размерность фазового пространства, в котором может существовать аттрактор, неизвестна заранее, то строятся фазовые пространства последовательно возрастающей размерности, и каждое из них просматривается с целью его поиска. Ввиду понятных трудностей просмотра многомерных пространств разработан косвенный метод обнаружения и оценки размерности аттрактора. Следуя [1], опишем его алгоритм.

Введем функцию C(R), используя соотношение

• 1       M M - 1

C(R) = М(М—1) g g @(R - X- j      (1)

j = 1

где Xi – одна из M точек n-мерного фазового пространства, Xj представляет массив из остальных (M─1) точек; Θ функция Хевисайда: Θ(x)=0 при x<0 и Θ(x)=1 при x>0. Введенная указанным способом функция C(R) позволяет сосчитать число точек в фазовом пространстве, отстоящих от точки Xi на расстояние, не превышающее некоторую величину R. Величина C(R) оказывается фактически мерой влияния точки Xi на другие точки Xj. Это дает основания рассматривать C(R) в качестве корреляционной функции аттрактора. В [1] показано, что при относительно малых R функция C(R) удовлетворяет соотношению ln C(R) = d lnR,                                  (2)

где d – размерность аттрактора, которая вводится как формальная функция от размерности фазового пространства n, в котором аттрактор рассматривается. Из этих соотношений вытекает следующий алгоритм.

• 1.    Используя исходную временную последовательность наблюдаемого параметра, построить фазовые пространства с возрастающей размерностью n=2,3,4, ... , содержащие по M точек.

• 2.    Для фазового пространства размерности n рассчитать корреляционную функцию C(R) в соответствии с (1).

• 3.    Определить угловой коэффициент d линейного участка графика зависимости (2) вблизи начала координат в фазовом пространстве размерности n.

• 4.    Построить график зависимости углового коэффициента d от размерности n фазового пространства, т.е. график функции d = f(n), и проанализировать его. Если величина d не выходит на насыщение при увеличении n, то система не имеет аттрактора. Если d имеет насыщение, то величину d в этом случае следует рассматривать как размерность аттрактора, представленного исходной временной последовательностью [1].

Таким образом, алгоритм поиска аттрактора и оценки его размерности сводится к построению графика функции d=f(n), выступающего как наглядный и чувствительный критерий обнаружения аттрактора при любой его размерности.

Информация о наличии и размерности аттрактора у исследуемой системы имеет большое значение для понимания ее динамики. Так, в частности, если размерность аттрактора – величина существенно дробная, то система способна к хаотическим колебаниям состояния независимо от того, действуют на нее или нет внешние случайные возмущения. Этот очень сильный результат исследований в области теории катастроф, полученный сравнительно недавно [1], показывает, что хаотическое поведение системы далеко не всегда можно идентифицировать как отклик ее на внешние воздействия. Во многих ситуациях оно обусловлено динамическими свойствами самой системы, и его следует рассматривать как равноправное с другими, имеющее свои особые механизмы возникновения.

С другой стороны, есть и еще один аспект в оценке роли устойчивости в динамике систем. Известно, что при наличии аттрактора с дробной размерностью наблюдается неустойчивость состояний равновесия системы [1]. Такая неустойчивость способна играть роль усилителя слабых внешних воздействий, включая и имеющих случайный характер. Таким образом, те воздействия, которые в устойчивом состоянии системы могли бы не оказать заметного влияния, в неустойчивом состоянии системы вызывают в ней усиленный отклик, создающий впечатление интенсивно действующих факторов.

Интерес к аттракторам этого типа резко возрос, когда было обнаружено, что странный аттрактор вызывает хаотическое, а по существу случайное поведение даже хорошо организованных детерминистических систем [2]. Такой аттрактор имеет сложную структуру. Внутри него фазовые траектории блуждают нерегулярным образом и чрезвычайно чувствительны к начальным условиям. Одной из особенностей странного аттрактора является то, что система способна совершить внезапный скачок после длительного периода кажущегося состояния покоя. Покажем на примере, какого рода информация может быть получена при использовании описанного подхода.

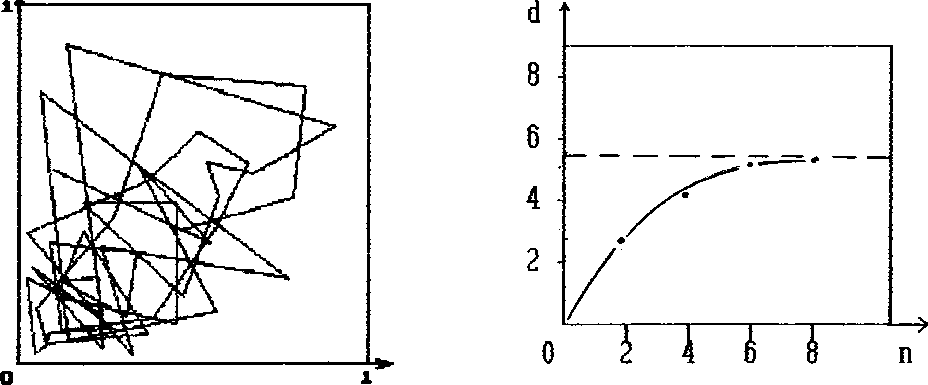
• а)    б)

Рисунок 1 – Отображение состояния технологической системы, производящей колготки детские из пряжи 11.8 текс х 2 (поставщик ГПНО “Гронитекс”): а) фазовый портрет системы в нормированных фазовых координатах Q[i], Q[i+1], (i=1, 2, 3,...n);

• б)    график функции d=f(n), определяющий размерность аттрактора

Рассмотрим технологическую систему в условиях ОАО “КИМ” (г. Витебск), производящго на двухцилиндровых чулочных автоматах 2АН-14 колготки детские из хлопчатобумажной пряжи линейной плотности 11.8текс х 2, вырабатываемой на Гродненском производственно-ниточном объединении “Гронитекс”. Фазовый портрет системы построен по последовательности Q i значений отходов на стадии вязания; здесь i=1, 2, 3,...n – номер рабочей смены, по истечении которой регистрируются отходы Q i , N – длина последовательности. На рис. 1а хорошо видно, что система имеет аттрактор. Оценка его размерности по графику функции d=f(n), представленному на рис. 1б, выходящей на насыщение при n, показывает, что аттрактор странный, т.к. его размерность d =5,5.

Рассмотрим теперь ситуацию, когда те же изделия, на тех же машинах вырабатывались из хлопчатобумажной пряжи той же линейной плотности, но произведенной на Барановичском производственном хлопчатобумажном объединении (БПХО). Фазовый портрет этой системы, построенный аналогично, представлен на рис. 2. И здесь мы видим резкие уходы с аттрактора. Однако они более редки, чем в предыдущем примере.

а)

б)

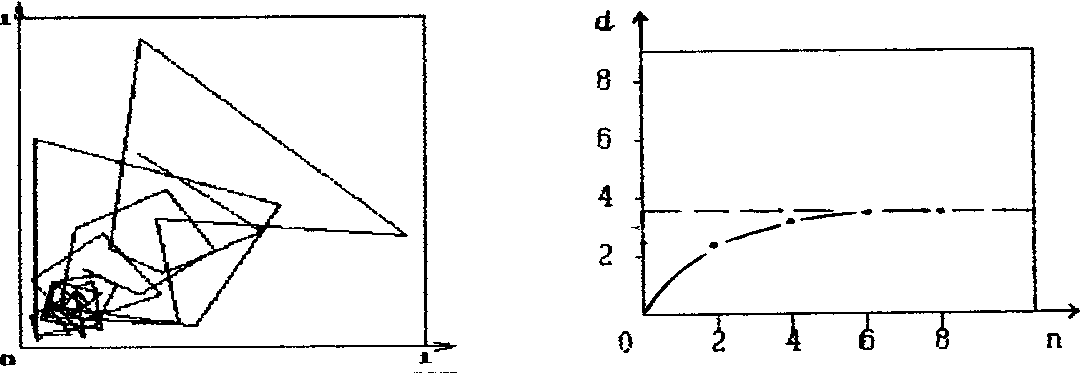
Рисунок 2 – Отображение состояния технологической системы, производящей изделия арт. 3С122 из х/б пряжи 11.8 текс х 2 (поставщик БПХО); а) фазовый портрет системы в фазовых координатах Q[i], Q[i+1], (i=1,2,3,...N); б) график функции d=f(n), определяющий размерность аттрактора

По-прежнему размерность аттрактора выражается дробным числом. Однако при использовании пряжи первого поставщика (БПХО) состояние технологической системы определяется тремя ключевыми параметрами, в то время как применение пряжи второго поставщика (ГПНО) увеличивает до 5 число ключевых факторов, обусловливающих поведение соответствующей технологической системы. Такой факт невозможно установить с позиций математической статистики. В этом и состоит принципиальная ценность предлагаемого подхода к анализу систем в трикотажном производстве.

Важным преимуществом предлагаемого подхода к оценке устойчивости технологических систем является отсутствие необходимости иметь какие-то особые данные или данные, получаемые особыми методами. Как видно из представленного примера, совершенно новую информацию можно получить из временных рядов значений величины отходов на стадии вязания. Эта величина очень проста и доступна в измерительном отношении, а главное – широко используется на практике. Подобный анализ может быть проведен с использованием временных рядов значений любого параметра системы, обладающего достаточным уровнем полноты отображения интересующих нас свойств этой системы. Поэтому предлагаемый подход вполне универсален.

Всё, изложенное выше, показывает, что оценка устойчивости технологических систем путем анализа их состояния в фазовом пространстве позволяет видеть такие особенности их динамики, которые делают видимыми различия в важных интегральных свойствах систем, которые недоступны при других, в том числе статистических, подходах.