Неупругое деформирование и прочность однонаправленных композитов при продольном сдвиге

The mathematical model for investigation of the nonelastic and fracture processes in unidirectional fiber-reinforced composites under longitudinal shear loading is presented. The stress and strain fields in fibers and matrix are calculated by method of local approximation from the solution of antiplane boundary-value problems for structural fragments with tetragonal fibers arrangement. The matrix constitutive equations include formulas of deformation theory of plastisity and shear modulas reduction relations for zones where a strength criterion is violated. Fibers were elastic and nonfructured. The boundary forces for structural fragment are given by steps in accord with simply longitudinal shear loading conditions. Epoxy composites with fibers from glass, carbon, boron and kevlar were considered. Volume fraction of fibers were 0.58 and 0.72. Stress and strain fields in matrix and fibers were calculated. Macrostress and macrostrain for the composites were obtained from the averaging ones.Nonlinear macrostress-macrostrain diagrams were constructed. Composite strength was estimated from the analysis of fracture processes in matrix. The results were correlated with experimental and calculated date presented in the literature .

Исследования, проведенные рядом авторов [1,2,3], показали, что момент, когда сдвиговые напряжения в критических зонах армированного пластика достигают значений прочности связующего, не всегда является началом лавинообразного разрушения материала. Микротрещины, возникающие в полимерном связующем перпендикулярно направлению действия максимальных растягивающих напряжений, имеют возможность равновесно развиваться вследствие перераспределения нагрузки на соседние области матрицы. В работе [1] для моделирования указанного механизма использовалось представление об условном течении полимерного связующего при достижении напряжениями сдвига критического значения. Напряженно-деформированное состояние в компонентах пластика рассчитывалось по методу сечений, пренебрегая взаимодействием соседних волокон. По мере нагружения зона условной текучести распространялась по всей матрице, обуславливая значительную нелинейность диаграммы деформирования композита при продольном сдвиге.

В настоящей работе для моделирования процессов неупругого деформирования и разрушения однонаправленных композитов при продольном сдвиге используется метод локального приближения , учитывающий взаимодействие ближайших соседних волокон [4]. Напряженно-деформированное состояние в волокнах и связующем композита рассчитывается на структурном фрагменте с регулярной тетрагональной упаковкой девяти цилиндрических волокон. Математическая постановка антиплоской физически нелинейной задачи для области V ,соответствующей структурному фрагменту, заключается в отыскании минимума функционала Лагранжа

^{S J} = ¹ J ( Y 13 G 13 ^sy 13 + y 23 G 23 s y 23 )dV - J F s wdS , 2 Vs

где Sw - вариация перемещений в направлении оси OX3, совпадающей с направлением волокон,    y , y , S y , Sy y 13 y 23 i 13 i 23

-

деформации сдвига и их вариации, являющиеся

ненулевыми в поставленной задаче, F - внешние силы на границе S структурного фрагмента, действующие в направлении оси OX . Многосвязная область V состоит из подобластей V^(K) , соответствующих матрице (k=1) и волокнам (k=2), на границе подобластей задаются условия идеального контакта. Дополнительными условиями для функционала (1) являются геометрические уравнения

dw

dw

^{y 13}    d X₁; ^{y 23}    d X₂

.

Физические соотношения для матрицы включали уравнения деформационной теории пластичности на участке активного нагружения и редуцирования жесткости, в случае нeвыполнения критерия прочности

Т а 3 < Г > = G> . ^ф ) Y a 3 ( r )’

( Ф>0 ),

а = 1,2

Ga 3 = 1

Ga3(i - ®(а, ф  о о, ф> о ,

1   ²²

-i = ^(д y +У.

Волокна считались упругими и

неразрушаемыми.В качестве критерия прочности

использовался критерий Мизеса, принимающий в данной постановке вид

23 — ¹ <  ”.

Величину внешних сил F на границе S подбирали таким образом, чтобы напряжения Т ₁₃, Т ₂₃, осредненные по центральной ячейке периодичности фрагмента, равнялись макроскопическим т ₁₃ , Т_{2 3} [4]. Макроскопические напряжения в данной работе задавались по шагам в соответствии с условиями простого нагружения :

т * = _T0 (1 + a k)

^Т .    ^Т 23         ,     k=1,2 N

Т13 = 0, с шагом =1 до начала разрушения матрицы и далее с шагом =0.25 по формулам

т„ = t” (1 + aN + pk)

^{Т 23 Т 23}                 ,       k=1,2,...,M

*

Т 13 = 0.

Начальное значение макронапряжений т 0₃ принималось равным 10 МПа.

Поставленная антиплоская задача решалась МКЭ с использованием конечноэлементной сетки, содержащей 1400 узлов, 2700 элементов, характер триангуляции структурного фрагмента с объемной долей волокон vf=0.58 показан на рис.1 .

Рис. 1. Триангуляция структурного фрагмента.

Исследовалось несколько типов полимерных пластиков со следующими характеристиками компонентов :

• •    матрица - эпоксидная смола ЭДТ-10,G=1073 МПа ,p=0.0158 МПа (что соответствует пределу прочности на сдвиг порядка 45 МПа), функция ω ( ε i ) рассчитывалась на основе диаграммы τ - γ (рис 2,а), построенной по данным работы [5];

• •    матрица - эпоксифенольная смола, G =1500 МПа , p=0.0158 , линейная модель [1];

• •    высокомодульное стекловолокно, G=41322 МПа [6];

• •    стекловолокно на основе Е-стекла, G=30578 МПа [6];

• •    бороволокно, G=160 000 МПа [6];

• •    углеволокно, G=47000 МПа [6];

• •    органоволокно, G=2400 МПа [7].

Тестирование программного комплекса проводилось путем сравнения эффективного модуля сдвига и полей напряжений в компонентах высокомодульного стеклопластика (G(2) / G(1) =38.5 , vf=0.58 ), полученных в результате решения упругой задачи аналитическим методом в рядах [1] и численным по разработанной программе. Сравнение показало, что в области максимальных концентраций отличие напряжений на межфазной поверхности составляло не более 7% , отличие эффективных модулей - 5%.

На рис.2 приведены диаграммы деформирования τ ₂ ^* ₃ - γ ₂ ^* ₃ высокомодульного стеклопластика с объемной долей волокон 0.58 , построенные по осредненным значениям полей напряжений и деформаций в центральной ячейке периодичности структурного фрагмента. Анализ результатов показывает, что возникновение зон разрушения полимерной матрицы на начальном этапе не влияет на характер диаграмм.

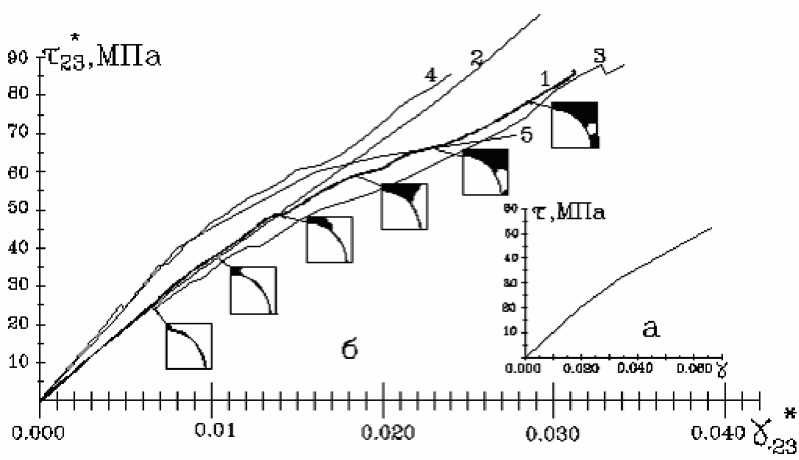
Рис. 2. Диаграммы деформирования эпоксидного связующего (а) и эпоксидного (1-3) и эпоксифенольного (4,5) стеклопластика (б) vf=0.58: 1-нелинейная модель с разрушением; 2-нелинейная модель без разрушения; 3,4- линейная модель с разрушением; 5-эксперимент [1]

При достижении размера разрушенной зоны S_r порядка 16% от площади матрицы и выше наблюдается более заметное отклонение от линейной зависимости. Сравнение различных вариантов физических соотношений (рис. 2,б) позволяет сказать, что для корректного моделирования диаграммы τ ₂ ^* ₃ - γ ₂ ^* ₃ композита учет возможности разрушения матрицы посредством редуцирования жесткости в уравнениях (3) является более важным фактором, чем учет нелинейного деформирования. Однако при использовании для матрицы нелинейной модели процесс развития поврежденных зон является более медленным (кривая 1 на рис.2,б лежит выше кривой 3). Сравнение результатов расчета с экспериментальной диаграммой для эпоксифенольного стеклопластика показывает, что физические соотношения для матрицы, моделирующие разрушение занулением модуля сдвига в соответствующих зонах, позволяют качественно описать характер деформирования однонаправленного композита при продольном сдвиге.

На рис.3 представлены рассчитанные диаграммы деформирования для нескольких типов эпоксидных пластиков с объемными долями волокон 0.58 и 0.72, а также экспериментальная диаграмма для углепластика из работы [8]. Видно, что с увеличением объемной доли волокон нелинейность диаграмм уменьшается. При этом увеличивается отличие диаграмм для различных типов пластиков, что согласуется с аналитическими оценками эффективных модулей продольного сдвига для однонаправленных композитов [9]. Уровень макронагрузки, соответствующей началу структурного разрушения, для боро-, угле- и стеклопластиков примерно одинаков: 20-21 МПа при vf=0.72 и 27-28 МПа при vf=0.58.

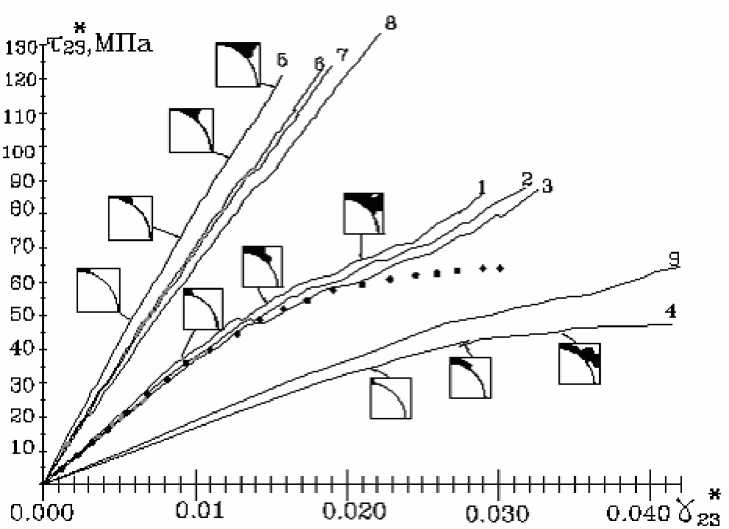
Рис.3. Диаграммы деформирования эпоксидных пластиков с объемной долей волокон 0.58 (1-4) и 0.72 (5-9) : 1,5- боропластик; 2,6- углепластик; 3,8-стеклопластик на основе Е-стекла; 4,9- органопластик; 7-высокомодульный стеклопластик; точками показана экспериментальная диаграмма для эпоксидного углепластика [5]

Интересно отметить, что хотя разрушение в матрице композитов с объемной долей волокон 0.72 начинается при меньших нагрузках , дальнейшее увеличение разрушенной области происходит более медленными темпами, например,для стеклопластика из Е-стекла vf=0.72 при τ ₂ ^* ₃ =49 МПа размер разрушенной зоны Sr =6% от площади матрицы, а для аналогичного композита с vf =0.58 ,при τ ₂ ^* ₃ =49 МПа - Sr =35%. Это обстоятельство приводит к выводу, что с увеличением коэффициента армирования прочность при продольном сдвиге повышается. Данное заключение противоречит работам [1,2], в которых отмечается, что прочность композита при продольном сдвиге не зависит от коэффициента армирования , либо уменьшается с его увеличением. Отсутствие данных по коэффициентам армирования и свойствам матриц у большинства экспериментальных результатов не позволяет провести проверку полученного вывода.

В целом диаграммы деформирования исследованных композитов при соответствующей обьемной доле являются подобными, как и характер процессов разрушения, протекающих в матрице. Исключение составляет эпоксидный органопластик. В связи с малым модулем сдвига волокон поле напряжений в структуре данного композита более однородно, поэтому области разрушения существенно увеличиваются при небольших изменениях внешней нагрузки, что приводит к значительной нелинейности диаграмм деформирования. Увеличение коэффициента армирования, в связи с вышеуказанным обстоятельством мало влияет на характер диаграмм τ2*3 -γ2*3 и на уровень нагрузок, соответствующих началу разрушения матрицы: τ2*3 =33.7 МПа, vf =0.72 и τ2*3 =34.0 МПа , vf=0.58.

Прочность композита предлагается оценивать анализируя характер развития областей разрушения : можно считать, что композит утратил несущую способность, если разрушенная область расположена вдоль всей стороны ячейки периодичности либо по всей межфазной поверхности. Для высокомодульного стеклопластика с vf =0.58 такая ситуация возникает при τ ₂ ^* ₃ =65 МПа, при этом размер разрушенной зоны составляет порядка 45% от площади матрицы. Полученная оценка попадает в диапазон экспериментальных значений сдвиговой прочности однонаправленных стеклопластиков 57-76 МПа с коэффициентами армирования 0.5-0.62, приведенный по данным различных источников в работе [1]. Оценка прочности композитов предложенным способом дает для боро-, угле- и стеклопластика приблизительно одинаковый уровень предельных напряжений порядка 63 МПа при vf =0.58 и порядка 120 МПа при vf =0.72. Для органопластика в качестве оценки прочности можно взять уровни нагрузки 40 МПа ( vf =0.58) и 48 МПа ( vf =0.72), предшествующие скачкообразному увеличению разрушенной области с 16 до 40% при vf= 0.58 и с 7% до 38% при vf =0.72. Приведённые оценки согласуются с диапазонами экспериментальных данных : органопластик - 15-37 МПа [10], 43-46 МПа [3], 20-44 МПа [6], 60-62 МПа [11]; углепластик - 43-53 МПа [11] и 67-127 МПа[3]; боропластик - 46 МПа [12], 60 МПа [6].

Заключение .

Моделирование структурных процессов неупругого деформирования и разрушения на основе уточненных расчетов полей напряжений и микродеформаций по разработанной модели показало возможность описания нелинейных диаграмм деформирования полимерных композитов при продольном сдвиге. Процесс развития зон разрушения в матрице является устойчивым. Сдвиговая прочность композита, прогнозируемая на основе анализа численных фрактограмм, соответствует экспериментальным результатам.