Неупругое поведение и разрушение материалов при изотермических и неизотермических, простых и сложных нагружениях
Автор: Бондарь В.С., Абашев Д.Р.
Статья в выпуске: 4, 2020 года.
Бесплатный доступ
Рассматривается математическое моделирование процессов неупругого поведения и разрушения конструкционных материалов (сталей и сплавов) при простых и сложных, изотермических и неизотермических нагружениях в условиях повторности и длительности воздействия термомеханических нагрузок. Математическое моделирование осуществляется на основе прикладной теории неупругости, относящейся к классу теорий течения при комбинированном упрочнении. Формулируются основные положения и приводится сводка основных уравнений прикладной теории неупругости. Определяются материальные функции, замыкающие прикладную теорию неупругости, и приводится связь определяющих функций с материальными. Результаты расчетов на основе прикладной теории неупругости сопоставлены с результатами экспериментов. Во всех представленных исследованиях неупругое деформирование осуществляется в условиях повторности и длительности воздействия термомеханических нагрузок. Рассматривается неупругое деформирование образцов из алюминиевого сплава АЛ-25 при одноосном растяжении-сжатии как при изотермическом, так и неизотермическом циклическом нагружении. Неупругое деформирование при сложном нагружении по двузвенным ломаным траекториям деформаций с различными скоростями деформирования в условиях высокой температуры исследуется на трубчатых образцах из сплава 30ХГСА. Рассматривается неупругое деформирование трубчатых образцов из нержавеющей стали 304 при сложном нагружении в условиях повышенной температуры. Осуществляется мягкое циклическое нагружение по двузвенным траекториям напряжений с различными углами изломов. В конце звеньев траектории напряжений осуществляется выдержка в течение 8 ч. Анализируются результаты расчетов по различным теориям, применяемым в практических расчетах. Рассматривается неупругое деформирование и разрушение образцов из нержавеющей стали 12Х18Н9 при жестком циклическом деформировании в условиях как изотермических, так и неизотермических нагружений. Длительность цикла нагружения составляет 4 мин, что позволяет при высокой температуре проявиться эффектам залечивания и охрупчивания. Наблюдается существенное отличие (почти на порядок) числа циклов до разрушения при синфазных и противофазных режимах изменения силовой деформации и температуры.
Неупругое поведение, разрушение, простые и сложные нагружения, изотермические и неизотермические нагружения, повторные и длительные нагружения
Короткий адрес: https://sciup.org/146282009
IDR: 146282009 | УДК: 539.374 | DOI: 10.15593/perm.mech/2020.4.10
Текст научной статьи Неупругое поведение и разрушение материалов при изотермических и неизотермических, простых и сложных нагружениях
ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2020PNRPU MECHANICS BULLETIN
Адекватное описание процессов неупругого поведения и разрушения конструкционных сталей и сплавов при повторных и длительных воздействиях термомеханических нагрузок до сих пор остается актуальной проблемой оценки и прогнозирования выработанного и остаточного ресурса конструкций высоких параметров. Математическому моделированию таких процессов посвящено большое количество исследований, среди которых в классе дифференциальных теорий следует отметить работы А.А. Ильюшина [1, 2], В.В. Новожилова [3], Ю.Н. Работнова [4], И.А. Биргера [5], В.С. Бондаря [6–15], Р.А. Васина [16], Ю.И. Кадашевича [3], Л.М. Качанова [17], Ю.Г. Коротких, И.А Волкова и Л.А. Игумнова [18–21], С.А. Капустина [22], Н.Н. Малинина [23], Ю.М. Теми-са [24], Кремпла [25, 26], Криега [27–29], Леметри [30], Линхольма [31], Миллера [32–34], Оно [35–38], Харта [39], Шабоша [40–45] и др.
Наибольшее распространение в практических расчетах в настоящее время нашли прикладные варианты теории течения, базирующиеся на концепции комбинированного упрочнения. Среди этих вариантов теорий теории Шабоша [40–45], Ю.Г. Коротких [18–21] и В.С. Бондаря [6–15] являются достаточно экспериментально обоснованными и широко применяемыми для расчетов ресурса материалов конструкций. В работе [11] изложены основные положения и уравнения прикладной теории не-упругости, приведены материальные функции, базовый эксперимент и метод идентификации материальных функций на основе базового эксперимента. Рассмотрен пример определения материальных функций нержавеющей стали 12Х18Н9. Приведены варианты прикладной теории неупругости и требуемое число материальных функций для каждого варианта. Дан перечень экспериментов и конструкционных материалов, на которых была проведена верификация прикладной теории неупругости.
В настоящей работе формулируются основные положения и приводится сводка основных уравнений прикладной теории неупругости [11]. Определяются материальные функции, замыкающие прикладную теорию неупругости, и приводится связь определяющих функций с материальными. Указывается базовый эксперимент и метод идентификации материальных функций.
Далее рассматриваются результаты некоторых оригинальных экспериментальных исследований, которые сопоставляются с результатами расчетных исследований на основе прикладной теории неупругости. Во всех исследованиях неупругое деформирование осуществляется в условиях повторности и длительности воздействия термомеханических нагрузок. Рассматривается не- упругое деформирование образцов из алюминиевого сплава АЛ-25 при одноосном растяжении-сжатии как при изотермическом, так и неизотермическом циклическом нагружении. Неупругое деформирование при сложном нагружении по двузвенным ломаным траекториям деформаций с различными скоростями деформирования в условиях высокой температуры исследуется на трубчатых образцах из сплава 30ХГСА. Рассматривается неупругое деформирование трубчатых образцов из нержавеющей стали 304 при сложном нагружении в условиях повышенной температуры. Выполняется мягкое циклическое нагружение по двузвенным траекториям напряжений с различными углами изломов. В конце звеньев траектории напряжений осуществляется выдержка в течение 8 ч. Анализируются результаты расчетов по различным теориям, применяемым в практических расчетах. Рассматривается неупругое деформирование и разрушение образцов из нержавеющей стали 12Х18Н9 при жестком циклическом деформировании в условиях как изотермических, так и неизотермических нагружений. Длительность цикла нагружения составляет 4 мин, что позволяет при высокой температуре проявиться эффектам залечивания и охрупчивания. Наблюдается существенное отличие (почти на порядок) числа циклов до разрушения при синфазных и противофазных режимах изменения силовой деформации и температуры.
1. Основные положения и уравнения прикладной теории неупругости
f ( G y ) = 2 ( s ij - a y )( s ij - ay ) - C 2 = °. (3)
C = qEEи *+ qTT - qR, e - * = | 3 ey ey J .(4)
(2 . , A (2 „
+ — ТТЕ.. + gT'a T— — gR E-+ gR a .
I з ge j ga zy I I з ge zy ga j I"V^/
е - =^L;i = 3 j e ‘j dG i 2 *
G и
* 3 1
' и * , s ij = s ij — a y , G u = (2 s y s y Y2
.
е
н и *
E *
c. =------
U E, + 3 G *
1 s * rr
3 ^^^ L - bTt + B R
2 G U
S * ( Ey.-«TTT ) .
3 G i ^_L - b t t + B R
__*
G U
- * *
E * = q e + g + g e e и + g a a u , BT = q T + g T E - * + gTaa* u , B R = q R + g R e - * + g R a * ,
S* £K
- * j 'jy e и = *
G u
au
3 s y a y G = E
2 G * , 2 ( 1 + v ) .
,
Материал однороден и начально изотропен. Рассматриваются только конструкционные стали и сплавы. В процессе неупругого деформирования в материале может возникать только неупругая деформационная анизотропия. Рассматриваются малые деформации при температурах, когда нет фазовых превращений, и скоростях деформаций, когда динамическими эффектами можно пренебречь. Случаи больших градиентов температур не рассматриваются.
Анализируется весьма простой вариант прикладной теории неупругости [11], являющийся частным вариантом теории неупругости [6]. Вариант теории относится к классу теорий течения при комбинированном упрочнении.
Далее приводится сводка основных уравнений прикладной теории неупругости.
^u =e e +e - . (1)
g u < C U e u * < ° - упругость, g U = C A e - * > ° - неупругость.
«- 1 a j e -,
6) = am a —— - g mto . W m
W = g W T - g w W . (1°)
е ey = E [ G y - v ( 3 G ° 5 y -G y ) ] + a T T ,
a j = a t% - ^ 2 [G j -v ( 3 G ° 5 y -G y ) ]x
dE
(3o05f/ dT E 0 j
\ dv
G y ) dT ’
Здесь и далее компоненты тензоров записываются в базисе декартовой ортогональной лабораторной системы координат; e iy , e j, e - - тензоры скоростей общей,
*
упругой и неупругой деформаций; G y , S y , S y , a iy - тензор напряжений, девиаторы напряжений, активных напряжений и микронапряжений; e - , - накопленная неупругая деформация; f ( G y ) = ° - поверхность нагружения; С – размер (радиус) поверхности нагружения; E , v , a T - модуль Юнга, коэффициент Пуассона, коэффициент температурного расширения; m - повреждение; W - энергия разрушения; q Е , q T , q R , g , g E , g a , g R , g aT , g R , g R , a , g m, g T , g w - определяющие функции, связь которых с материальными будет приведена ниже. Следует отметить, что здесь нет условного разделения неупругой деформации на деформации пластичности и ползучести. В эволюционном уравнении для радиуса
поверхности нагружения С первое слагаемое отвечает механическому упрочнению (разупрочнению, стабилизации), второе слагаемое обеспечивает неизотермический переход, а третье – возврат механических свойств при отдыхе, отжиге. В эволюционном уравнении для микронапряжений aij (смещение центра поверхности нагружения) первые три слагаемых описывают процессы образования и снятия микронапряжений при неупругом деформировании, два следующих обеспечивают неизотермический переход, а два последних – снятие микронапряжений при отдыхе, отжиге. Последние параметры в эволюционных уравнениях для C и aij являются функциями повреждения, что позволяет описать разупрочнение материала перед разрушением. В эволюционном уравнении для повреждений первое слагаемое описывает нелинейный процесс накопления повреждений за счет работы микронапряжений на поле неупру-гигих деформаций, второе слагаемое описывает процесс залечивания повреждений. В эволюционном уравнении для энергии разрушения первое слагаемое обеспечивает неизотермический переход, второе слагаемое описывает изменение энергии разрушения за счет охрупчивания. Критерием разрушения материала является достижение повреждением предельного значения, обычно принимаемого равным единице.
2. Материальные функции
Прикладную теорию неупругости замыкают следующие материальные функции:
-
E ( T ) , v ( T ) , a T ( T ) - упругие параметры;
Ea (T), О a (T), P( T) - модули анизотропного уп- рочнения;
C p ( T , e U • ) — функция изотропного упрочнения;
-
W0 ( T ) - начальная энергия разрушения;
-
be ( T ) , b a ( T ) , " e ( T ) , " a ( T ) , m to ( T ) - параметры изотропной и анизотропной ползучести;
b ^ ( T ) , b p( T ) , " ( T ) , n p( T ) - параметры залечивания и охрупчивания.
Определяющие функции выражаются через материальные следующим образом:
дC p C дC p
q„ = —, Qt =--”
e д e „" * TT C p dT
Q r = q e Pe ,
g = Ea + PO a , g e =P Ea , g a =-P ,
TT = dEa _ E a d O „T = 1 d О a g e dT о a dT , g a о a dT ’
P ge = gePa , ga =(g + gaau ) ~, aи
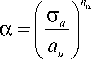
g to ^ , gW P , gW
W dW 0
W 0 dT ,
P e = exp ( b e ) C - C p 0| " c ( 1 -to ) - m " ,
P a = exp ( b a )( a „ ) "a ( 1 -to )- m to ,
' 0, если o„ > 0,
X = ^ ,„
_ exp ( b l)| o„|l, если o„ < 0,
P = exP ( b р ) ( О и ) " P ,
( 3 ) 2 ( 3 )2
и \ 2 ij i / , и I 2 ii ij J ,
C p 0 = C p ( T ,0 ) = ^ - , .
Здесь О - , - предел длительной прочности (предел ползучести); n a - параметр нелинейности процесса накопления повреждений ( n a = 1,5 ) .
Базовый эксперимент включает в себя испытания на одноосное циклическое деформирование и разрушение, а также ползучесть и длительную прочность при различных уровнях температур [6, 11]. Метод идентификации построен на обработке результатов базовых экспериментов.
3. Неупругое деформирование при изотермическом и неизотермическом циклическом нагружении
Рассматривается жесткое ( контролируемая деформация) циклическое нагружение материала при постоянной (изотермическое нагружение) и переменной (неизотермическое нагружение) температурах. При нагружении образцов реализуется одноосное напряженное состояние. В процессе экспериментов контролировалась осевая деформация en . Экспериментальные исследования [46] проводились на образцах из алюминиевого сплава АЛ-25. Циклическое деформирование образцов осуществлялось при постоянных температурах 150, 250 и 350 °С. Симметричные циклы имели размах деформации Ae t1 = 0,0065, а деформирование осуществлялось со скоростью £ 11 = 10 - 4 c - 1. При данной скорости деформирования временные эффекты (ползучесть) становились заметными уже начиная с температуры 250 °С.
Экспериментальные диаграммы циклического деформирования при температурах 250° и 350 °С приведены на рис. 1, 2 соответственно. Показаны 1-й, 10-й и 40-й циклы нагружения кружками, квадратиками и треугольниками соответственно. При рассмотренных температурах наблюдается циклическое разупрочнение с последующей стабилизацией после 40-го цикла. Имеет место и существенное влияние временных эффектов (ползучести), особенно при температуре 350 °С.
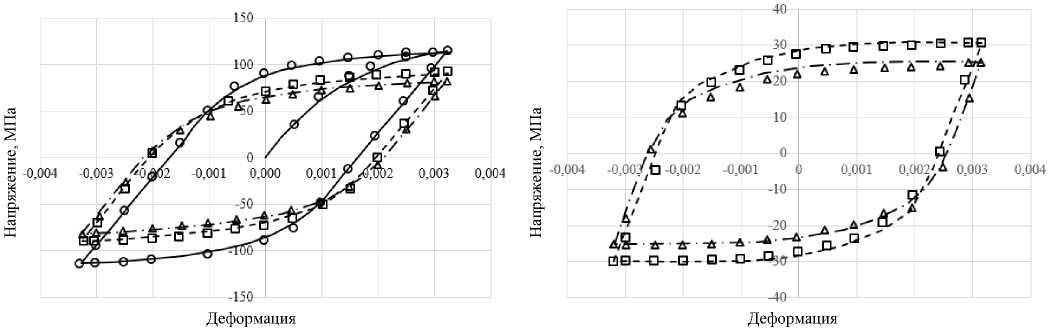
Рис. 1. Расчетные и экспериментальные циклические диаграммы при температуре 250 °С
Fig. 1. Calculated and experimental cyclic diagrams at a temperature of 250 °С
Рис. 2. Расчетные и экспериментальные циклические диаграммы при температуре 350 °С
Fig. 2. Calculated and experimental cyclic diagrams at a temperature of 350 °С
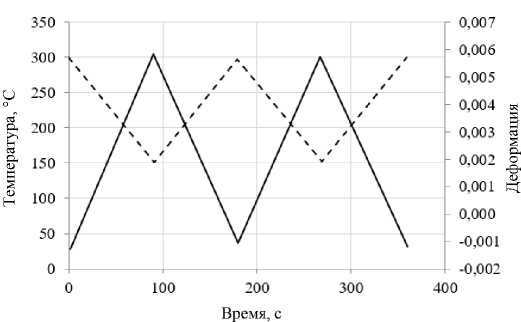
Рис. 3. Законы изменения температуры и силовой деформации
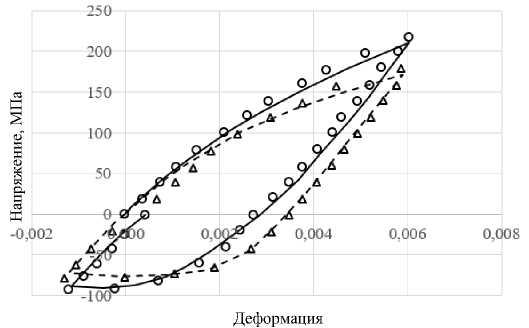
Рис. 4. Расчетные и экспериментальные циклические диаграммы при неизотермическом нагружении
-
Fig. 3. The laws of changes of temperature and force deformation
Экспериментальное исследование неизотермического нагружения проводилось [46] также на образцах из алюминиевого сплава АЛ-25. Задавался противофазный режим изменения температуры и силовой деформации (деформация за вычетом температурной).
Законы изменения температуры (пунктирная кривая) и силовой деформации (сплошная кривая) показаны на рис. 3. Диапазон изменения силовой деформации составляет 0,0012–0,0058, а температуры – 150–300 °С. Длительность цикла нагружения составила 180 с.
Экспериментальные диаграммы циклического деформирования для 1-го и 6-го циклов нагружения приведены соответственно кружками и треугольниками на рис. 4. При неизотермическом режиме также наблюдается циклическое разупрочнение материала.
Для проведения расчетов на основе прикладной теории неупругости [11] были использованы материальные функции алюминиевого сплава АЛ-25, приведенные в работе [6].
Расчетные циклические диаграммы изображены на рис. 1, 2, 4 сплошными, пунктирными и штрих-
Fig. 4. Calculated and experimental cyclic diagrams under non-isothermal loading
4. Неупругое деформирование при сложном нагружении с различными скоростями деформирования
пунктирными кривыми и близки к экспериментальным – отличие не превышает 10 %.
Экспериментальные исследования [47] проводились по программам жесткого нагружения с различными скоростями деформирования трубчатых образцов из сплава 30ХГСА при температуре 550 °C. Нагружение образца осуществлялось осевой силой и внутренним давлением, т.е. реализовывалось двухосное напряженное состояние и контролировались осевая и кольцевая деформации.
Рассматриваемая програмая включала в себя испытания по единой двузвенной ломаной траектории деформации в векторном пространстве Ильюшина [1, 2] (рис. 5), но с различными скоростями деформирования, которые были равны 5 ⋅ 10 - 3, 5 ⋅ 10 - 4, 1.65 ⋅ 10 - 4, 5 ⋅ 10 - 5 мин–1. Данная траектория деформации реализовывалась осевыми и кольцевыми деформациями растяжения.
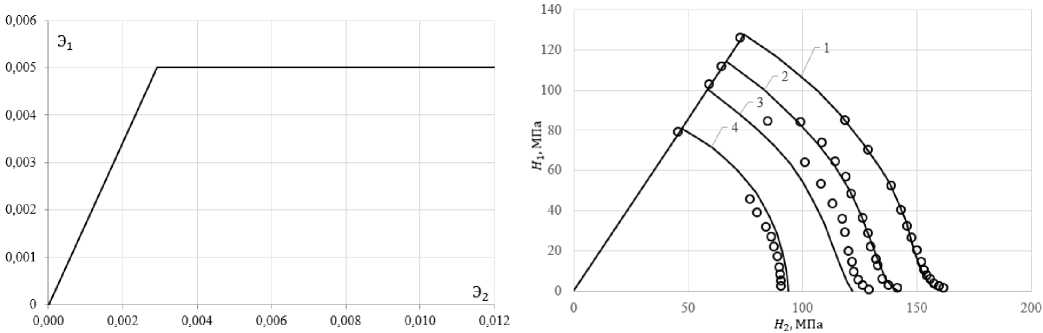
Рис. 5. Двузвенная ломаная траектория деформаций
Fig. 5. Two-link broken deformation trajectories
Рис. 6. Расчетные и экспериментальные траектории напряжений при разных скоростях деформирования
-
Fig. 6. Calculated and experimental stress trajectories at different strain rates
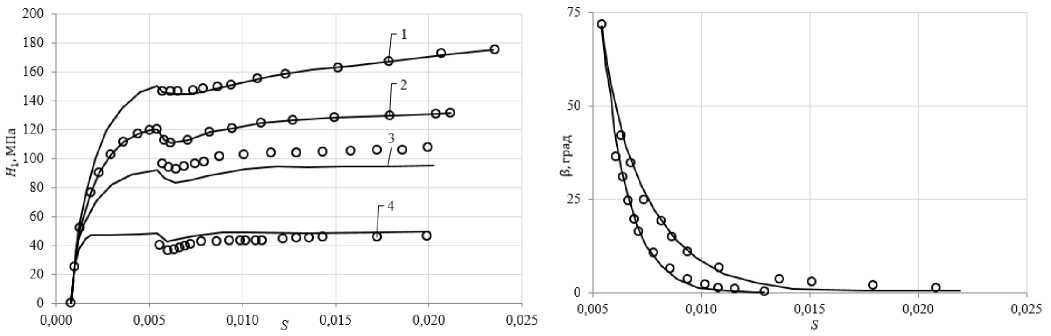
Рис. 8. Векторные свойства при различных скоростях деформирования
Рис. 7. Скалярные свойства при различных скоростях деформирования
Fig. 7. Scalar properties at different deformation rates
Fig. 8. Vector properties at different deformation rates
5. Неупругое деформированиепри сложном циклическом нагружении
Траектории деформаций и напряжений задавались в векторном пространстве Ильюшина [1, 2]. Скалярные свойства отображались зависимостью модуля вектора напряжений от длины траектории деформаций.
Векторные свойства отображались зависимостью угла между вектором напряжений и касательной к траектории деформаций от длины траектории деформаций.
Экспериментальные (кружки) ответные траектории напряжений приведены на рис. 6, скалярные и векторные свойства – на рис. 7, 8. Кривые на рисунках соответствуют различным скоростям деформаций. Наблюдается существенная зависимость результатов от скорости деформирования.
Для проведения расчетов на основе прикладной теории неупругости [11] были использованы материальные функции сплава 30ХГСА при температуре 550 °С, приведенные в работе [6]. Расчетные траектории напряжений, скалярные и векторные свойства изображены на рис. 6–8 сплошными кривыми и близки к экспериментальным – отличие не превышает 10 %.
Верхние кривые соответствуют максимальной скорости деформирования 5 ⋅ 10 - 3 , а нижние – минимальной 5 ⋅ 10 - 5мин - 1.
Экспериментальные исследования [48] проводились на трубчатых образцах из нержавеющей стали 304 при постоянной температуре, равной 650 °С. Нагружение образца осуществлялось осевой силой и крутящим моментом, т.е. проводились ( Р , М )-опыты при мягком циклическом нагружении. На рис. 9 показаны задаваемые в испытаниях траектории напряжений и периодические изменения напряжений σ 11 и σ 12 . Каждый цикл нагружения состоял из быстрого кручения, выдержки (точка А ), быстрой разгрузки, быстрого совместного кручения и растяжения, выдержки (точка В ) и последующей быстрой разгрузки. Интенсивности напряжений в точках А и В имели равную величину 137,3 МПа.
Длительность выдержки составляла 8 ч. Нагружение и разгрузка проводились со скоростью 49 МПа/мин. Угол θ между векторами напряжений при их периодическом вращении в испытаниях задавался равным 30, 60, 90, 120, 150 и 180°. В работе [48] приведены результаты испытаний только при θ = 30, 90, 150 и 180°. Ниже будут рассмотрены результаты при θ = 90, 150 и 180°, как наиболее интересные.
Изменение сдвиговой деформации при выдержках при сложном циклическом нагружении для углов вращения вектора напряжений θ = 180, 150 и 90° приведены соответственно на рис. 10, 11 и 12, а изменение осевой деформации для углов вращения θ = 150 и 90° – на рис. 13, 14. На этих рисунках светлыми кружками показаны экспериментальные результаты [48]. В работе [48] приведены расчеты по различным теориям ползучести: теория деформационного упрочнения; модифицированная теория деформационного упрочнения [49]; теория кинематического упрочнения [50]; теория комбинированного упрочнения [51].
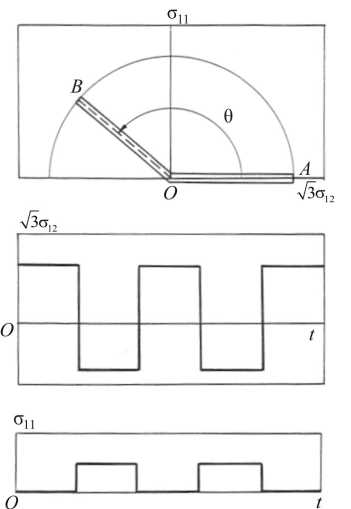
Рис. 9. Траектории напряжений и периодические изменения напряжений σ 11 и σ 12
Fig. 9. The trajectory of strain and the periodic changes of strain σ 11 and σ 12
При знакопеременном кручении (θ = 180°) в эксперименте наблюдается рост размаха деформации ползучести от цикла к циклу с последующей стабилизацией размаха на 4-м, 5-м циклах нагружения. Размахи деформации ползучести с увеличением номера цикла соответственно равны: 0,0025; 0,0026; 0,0027; 0,0028; 0,0028. Происходит также некоторое смещение цикла к симметричному.
Теория деформационного упрочнения даже качественно не отражает особенностей циклического деформирования. Модифицированная теория деформационного упрочнения после каждой смены знаков напряжения по- вторяет кривую ползучести, что также не соответствует эксперименту при циклической ползучести.
Теория кинематического упрочнения уже начиная практически со 2-го цикла дает симметричный цикл по амплитуде деформаций, превышающей почти в два раза экспериментальную. Теория комбинированного упрочнения (теория неупругости) также приходит к симметричному циклу, но начиная с 4-го, 5-го циклов нагружения. Амплитуда этих циклов почти в два раза меньше экспериментальной.
При вращении вектора напряжений на угол θ = 150° в эксперименте наблюдается стабилизация по амплитуде деформаций цикла начиная с 3-го, 4-го циклов. Средняя деформация цикла как у сдвиговой, так и у осевой компонент деформаций увеличивается от цикла к циклу, т.е. наблюдается одностороннее накопление деформаций, более значительное у осевой.
Из рассмотренных теорий только модифицированная теория деформационного упрочнения, и то только по осевой деформации, дает результаты, близкие к экспериментальным. По сдвиговой деформации отличие результатов расчетов по этим теориям и эксперимента значительное.
Были проанализированы результаты расчетов и эксперимента при угле вращения вектора напряжений на угол θ = 90°. Здесь также в эксперименте наблюдаются стабилизация по амплитуде деформаций цикла начиная с 3-го, 4-го цикла и одностороннее накопление деформаций, практически одинаковое для обеих компонент деформаций.
В этом опыте (θ = 90°) все рассматриваемые теории дают следующие результаты – отличие от эксперимента не превышает: 40 % для теории деформационного упрочнения, 30 % для модифицированной теории деформационного упрочнения, 20 % для теории кинематического и комбинированного упрочнения.
Результаты этих расчетов показывают, что рассмотренные теории не способны описать процессы неупругого деформирования как при простом, так и при сложном циклическом нагружении.
Для проведения расчетов на основе прикладной теории неупругости [11] были использованы материальные функции для нержавеющей стали 304 при температуре 650 °С, приведенные в работе [6].
Расчетное изменение сдвиговой деформации при выдержках для углов вращения вектора напряжений θ = 180, 150 и 90° приведены соответственно на рис. 10, 11 и 12, а изменение осевой деформации для углов вращения θ = 150 и 90° – на рис. 15, 16. На рис. 15, 16 приведены экспериментальные (светлые кружки) и расчетные (сплошные кривые) траектории деформаций для углов вращения θ = 150 и 90°. Расчетные результаты на основе прикладной теории неупругости близки к экспериментальным – отличие не превышает 10–15 %. На всех рисунках пунктирной кривой изображены результаты расчетов [52] на основе модели Коротких, и здесь отличие от эксперимента достигает 40 %. Сравнение результатов расчетов и экспериментов говорит о более адекватном соответствии эксперименту прикладной теории неупругости.
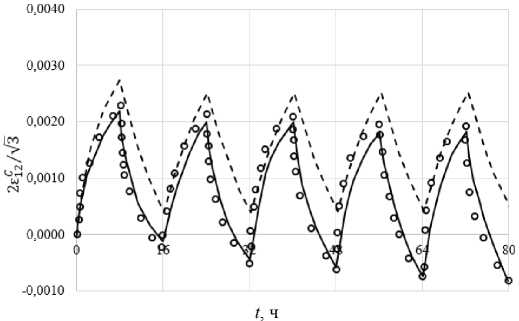
Рис. 10. Расчетные и экспериментальные зависимости сдвиговой деформации при выдержках для θ = 180°
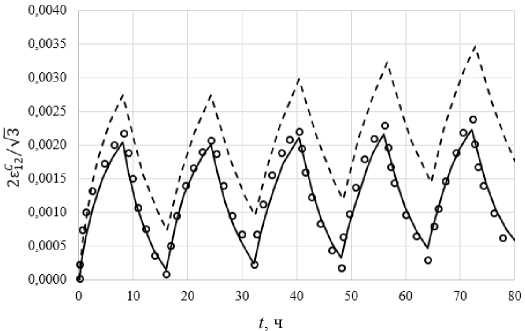
Рис. 11. Расчетные и экспериментальные зависимости сдвиговой деформации при выдержках для θ = 150°
Fig. 10. Calculated and experimental changes in shear deformation at exposure times for θ = 180°
Fig. 11. Calculated and experimental changes in shear deformation at exposure times for θ = 150°
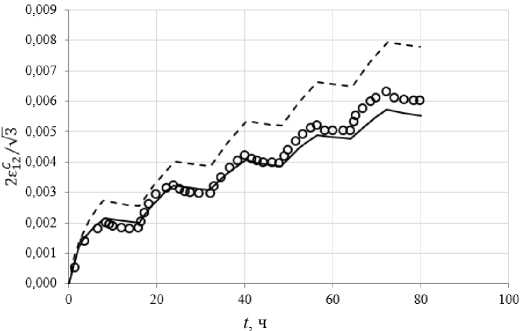
Рис. 12. Расчетные и экспериментальные зависимости сдвиговой деформации при выдержках для θ = 90°
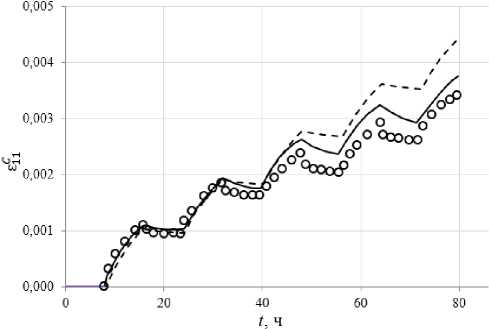
Рис. 13. Расчетные и экспериментальные зависимости осевой деформации при выдержках для θ = 150°
Fig. 12. Calculated and experimental changes in shear deformation at exposure times for θ = 150°
Fig. 13. Calculated and experimental changes in axial deformation at exposure times for θ = 150°
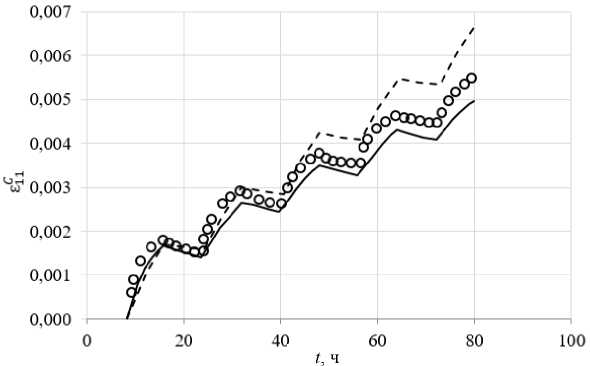
Рис. 14. Расчетные и экспериментальные зависимости осевой деформации при выдержках для θ = 90°
Fig. 14. Calculated and experimental changes in axial deformation at exposure times for θ = 90°
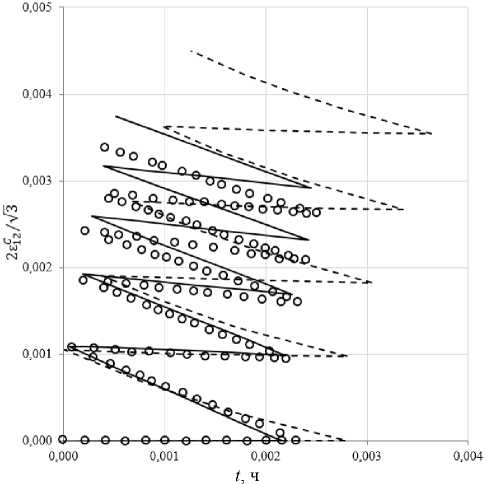
Рис. 15. Расчетная и экспериментальная траектории деформаций при выдержках для θ = 150°
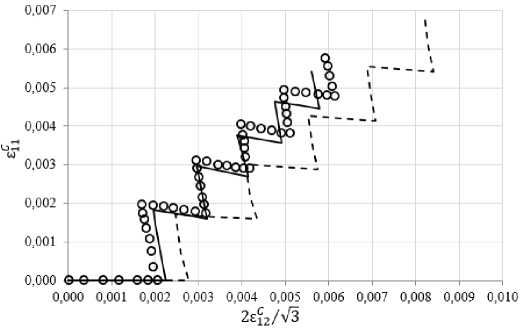
Рис. 16. Расчетная и экспериментальная траектории деформаций при выдержках для θ = 90°
6. Неупругое деформирование и разрушение при изотермических и неизотермических циклических нагружениях
Fig. 15. Calculated and experimental trajectories of deformations at exposures for θ = 150°
Fig. 16. Calculated and experimental trajectories of deformations at exposures for θ = 90°
Экспериментальные исследования [53] проводились на образцах из нержавеющей стали 12Х18Н9 при жестком циклическом деформировании в условиях как изотермических, так и неизотермических нагружений. Нагружение осуществлялось осевой силой ( Р -опыты). В процессе экспериментов задаются осевая силовая деформация (деформация температурного расширения исключается) и температура. Реализуется стационарное циклическое нагружение, т.е. законы изменения деформации и температуры от цикла к циклу не изменяются. Длительность цикла нагружения составляла 4 мин, что позволило при высокой температуре проявиться эффектам залечивания и охрупчивания. Циклическое нагружение проводилось до разрушения. Разрушение фиксировалось при образовании макротрещины, признаком образования которой являлось падение максимального напряжения на цикле при растяжении.
Реализовывались следующие режимы жесткого симметричного циклического деформирования с постоянной амплитудой силовой деформации, отличающиеся характером изменения температуры:
Режим 1 – температура постоянна и равна 650 °С (изотермический режим).
Режим 2 – температура изменяется синфазно деформации от 150 до 650 °С (неизотермический режим).
Режим 3 – температура изменяется противофазно деформации от 150 до 650 °С (неизотермический режим).
Для проведения расчетов на основе прикладной теории неупругости [11] были использованы материальные функции нержавеющей стали 12Х18Н9 при температурах 10, 150, 300, 500, 550, 600 и 650 °С, описанные в работе [6].
Расчетные и экспериментальные значения числа циклов до разрушения для трех амплитуд силовой деформации и трех режимов нагружения приведены в таблице. Расчетные и экспериментальные циклические диаграммы для всех режимов нагружения показали циклическое разупрочнение перед разрушением. Данный эффект есть результат зависимости неупругого поведения от повреждения. Аналогичный эффект имеет место и в механике поврежденной среды [18–21].
Накопление повреждений при сложном нагружении
The accumulation of damage under complex loading
|
H εα |
Режим |
N f рас |
N f экс |
|
0,04 |
1 |
47 |
45 - 55 |
|
2 |
11 |
10 - 15 |
|
|
3 |
49 |
45 - 55 |
|
|
0,02 |
1 |
154 |
150 - 180 |
|
2 |
26 |
25 - 30 |
|
|
3 |
161 |
150 - 180 |
|
|
0,01 |
1 |
391 |
380 - 450 |
|
2 |
72 |
70 - 80 |
|
|
3 |
406 |
380 - 450 |
Для изотермического режима с высокой температурой характерны интенсивные процессы охрупчивания и залечивания, при которых процесс охрупчивания более интенсивный. Процессы охрупчивания для синфаз- ного и противофазного неизотермических режимов одинаковы по интенсивности, но значительно уступают по интенсивности охрупчиванию на изотермическом режиме. Это объясняется различными временами воздействия высоких температур, при которых процессы охрупчивания более интенсивны. Синфазный неизотермический режим проходит без заметного залечивания повреждений, так как напряжения сжатия приходятся на область низких температур. Охрупчивание не успевает существенно повлиять на повреждения вследствие быстрого разрушения. Для противофазного неизотермического режима характерно большее залечивание, чем для синфазного, так как сжатие приходится на область высоких температур. Этим и объясняется большая долговечность на противофазном режиме, чем на синфазном. Большая долговечность на изотермическом режиме по сравнению с синфазным объясняется существенно большей интенсивностью залечивания, так как на изотермическом режиме весь процесс сжатия образца происходит при температуре 650 °С.
Таким образом, многообразие и сложность явлений, протекающих даже при стационарных циклических нагружениях, обусловливает необходимость рассматривать неупругое поведение и накопление повреждений как процесс вплоть до разрушения. Сопоставление результатов расчетов и экспериментов показывает их соответствие и подтверждает применимость прикладной
Список литературы Неупругое поведение и разрушение материалов при изотермических и неизотермических, простых и сложных нагружениях
- Ильюшин А.А. Пластичность. Основы общей математической теории. – М.: Изд. АН СССР, 1963. – 271 с.
- Ильюшин А.А. Механика сплошной среды. – М.: Изд-во МГУ, 1990. – 310 с.
- Новожилов В.В., Кадашевич Ю.И. Микронапряжения в конструкционных материалах. − Л.: Машиностроение, 1990. − 224 с.
- Работнов Ю.Н. Ползучесть элементов конструкций. – М.: Физматгиз, 1966. – 752 с.
- Термопрочность деталей машин: Справочник / под ред. И.А. Биргера, Б.Ф. Шорра. − М.: Машиностроение, 1975. − 455 с.
- Bondar V.S. Inelasticity. Variants of the theory. − New York: Begell House, 2013. − 194 p.
- Бондарь В.С., Даншин В.В., Кондратенко А.А. Вариант теории термовязкости // Вестник Пермского национального исследовательского политехнического университета. Механика. – 2016. – № 1. – С. 39–56. DOI: 10.15593/perm.mech/2016.1.03
- Бондарь В.С., Даншин В.В., Алхимов Д.А. Анализ циклического деформирования и мало-многоцикловой усталости в условиях одноосного напряженного состояния // Вестник Пермского национального исследовательского политехнического университета. Механика. – 2016. – № 4. – С. 52–71. DOI: 10.15593/perm.mech/2016.4.04
- Бондарь В.С., Абашев Д.Р., Петров В.К. Сравнительный анализ вариантов теорий пластичности при циклических нагружениях // Вестник Пермского национального исследовательского политехнического университета. Механика. – 2017. – № 2. – С. 23–44.
- Бондарь В.С., Абашев Д.Р., Петров В.К. Пластичность материалов при пропорциональных и непропорциональных циклических нагружениях // Вестник Пермского национального исследовательского политехнического университета. Механика. – 2017. – № 3. – С. 53–74. DOI: 10.15593/perm.mech/2017.3.04
- Бондарь В.С., Абашев Д.Р. Прикладная теория неупругости // Вестник Пермского национального исследовательского политехнического университета. Механика. – 2018. – № 4. – С. 147–162. DOI: 10.15593/perm.mech/2018.4.14
- Constitutive modeling of cyclic plasticity deformation and low-high-cycle fatigue of stainless steel 304 in uniaxial stress state / V.S. Bondar, V.V. Dansin, D.Vu. Long, D.D. Nguyen // Mechanics of Advanced Materials and Structures. – 2018. – Vol. 25(12) – P. 1009–1017. DOI: 10.1080/15376494.2017.1342882
- Бондарь В.С., Абашев Д.Р., Петров В.К. Некоторые особенности прогнозирования ресурса материалов и конструкций при циклическом нагружении // Вестник Пермского национального исследовательского политехнического университета. Механика. – 2019. – № 1. – С. 18–26. DOI: 10.15593/perm.mech/2019.1.02
- Бондарь В.С., Абашев Д.Р. Некоторые особенности процессов монотонных и циклических нагружений. Эксперимент и моделирование // Вестник Пермского национального исследовательского политехнического университета. Механика. – 2019. – № 2. – С. 25–34. DOI: 10.15593/perm.mech/2019.2.03
- Abashev D.R., Bondar V.S. Refinement jf plasticity theory for modeling monotonic and cyclic loading processes // Journal of Mechanics of Materials and Structures. – 2020. – Vol. 15, no. 2 – P. 225–239. DOI: 10.2140/jomms.2020.15.225
- Васин Р.А. Экспериментально-теоретическое исследование определяющих соотношений в теории упругопластических процессов: автореф. дис. … д.ф-м.н. – М.: МГУ, 1987. – 36 с.
- Качанов Л.М. Теория ползучести. – М.: ФИЗМАТЛИТ, 1960. – 455 с.
- Волков И.А., Коротких Ю.Г. Уравнения состояния вязкоупругопластических сред с повреждениями. − М.: ФИЗМАТЛИТ, 2008. − 424 с.
- Прикладная теория пластичности / Ф.М. Митенков, И.А. Волков, Л.А. Игумнов, А.В. Каплиенко, Ю.Г. Коротких, В.А. Панов. – М.: ФИЗМАТЛИТ, 2015. – 282 с.
- Волков И.А., Игумнов Л.А., Коротких Ю.Г. Прикладная теория вязкопластичности. Монография. – Нижний Новгород: Изд-во Нижегородского гос.университета, 2015. – 317 с.
- Волков И.А., Игумнов Л.А. Введение в континуальную механику поврежденной среды. – М. ФИЗМАТЛИТ, 2017. – 299 с.
- Капустин С.А., Чурилов Ю.А., Горохов В.А. Моделирование нелинейного деформирования и разрушения конструкций в условиях многофакторных воздействий на основе МКЭ. – Н. Новгород: Изд-во ННГУ, 2015. 347 с.
- Малинин Н.Н. Прикладная теория пластичности и ползучести. – М.: Машиностроение, 1975. – 400 с.
- Темис Ю.М. Моделирование пластичности и ползучести конструкционных материалов ГТД // Приоритеты развития отечественного автотракторостроения и подготовки инженерных научных кадров: материалы 49-й Междунар. науч.-техн. конф. ААИ. Школа-семинар «Современные модели термовязкопластичности». Ч. 2. – М.: МАМИ, 2005. – С. 25–76.
- Krempl E. The influence of state of stress on low-cycle fatigue of structural materials: a literature survey and interpretive report // Amer. Soc. Test. And Mater. Spec. Techn.Publ. – 1974. – № 549. – Р. 1–46.
- Krempl E., Lu H. The Hardening and Dependent Behavior of Fully Annealed AISI Type 304 Stainless Steel Under Biaxial in Phase and Out – of – Phase Strain Cycling at Room Temperature // ASME Journal of Engineering Materials and Technology. – 1984. – Vol. 106. – Р. 376–382.
- Krieg R.D. A. Practical Two Surface plasticity Theory // Journal of Applied Mechanics. – 1975. – Vol. 42. – Р. 641–646.
- Krieg R.D., Swearengen J.C., Rhode R.W. A physically based internal variable model for rate-dependent plasticity // Proc. ASME/CSME PVP Conference. – 1978. – Р. 15–27.
- Krieg R.D., Krieg D.B. Accurate of numerical solution methods for the elastic-perfectly plastic model // Trans. ASME. – 1977. – Vol. 199, no. 4. – Р. 510–515.
- Lemaitre Jean. Coupled elasto-plasticity and damage constitutive equations // Comput. Meth. Appl. Mech. and Eng. – 1985. – Vol. 51, no. 1–3. – Р. 31–49.
- Constitutive modeling for isotropic materials (HOST) / U.S. Lindholm, K.S. Chan, S.R. Bodner, R.M. Weber, K.P. Walker, B.N. Cassenti // Second annual contract report. – NASA CR – 174980. – 1985.
- Miller A.K. A unified approach to predicting interactions among creep, cyclic plasticity, and recovery // Nuclear Eng. and Design. – 1978. – Vol. 51. – Р. 35–43.
- Miller K.J., Brown M.W. Multiaxial fatigue: a brief review // Adv. Fract. Res. Proc. 6ts Int. Conf. New Delhi 4-10 Dec. – 1984. – Vol. I. – Р. 31–56.
- Miller A.K., Tanaka T.G. NONSS: A new method for integrating unified constitutive equations ander complex histories // Trans. ASME: J. Eng. Mater. and Technol. – 1988. – Vol. 110, no. 3. – Р. 205–211.
- Ohno N. A constitutive model of cyclic plasticity with a nonhardening strain region // J. Appl. Mech. – 1982. – Vol. 49. – Р. 721–727.
- Ohno N. Recent topics in constitutive modeling of cyclic and viscoplasticity // Appl. Mech. rev. – 1990. – Vol. 43. – Р. 283.
- Ohno N., Wang J.D. Transformation of a nonlinear kinematics hardening rulle to a multisurface form under isothermal and nonisothermal conditions // Int. Journal of Plasticity 7. – 1991. – Р. 879–891.
- Ohno N., Wang J.D. Kinematics hardening rule with critical state of dynamic recovery, Parts I and II // Int. Journal of Plasticity 9. – 1993. – Р. 375–403.
- Харт. Уравнения состояния для неупругой деформации металлов // Теоретические основы инженерных расчетов: Труды ASME. – 1976. – № 3. – C. 1–7.
- Chaboche J.L. Constitutive equation for cyclic plasticity and cyclic viscoplasticity // Inter. J. of Plasticity. – 1989. – Vol. 5, no. 3. – Р. 247–302.
- Chaboche J.L. Thermodynamically based viscoplastic constitutive equations: theory versus experiment // ASME Winter Annual Meeting, Atlanta, GA (USA). – 1991. – Р. 1–20.
- Chaboche J.L.Cyclic viscoplastic constitutive equations, parts I and II // ASME J. of Applied Mechanics 60. – 1993. – Р. 813–828.
- Chaboche J.L., Rousselier G. On the plastic an viscoplastic constitutive equations // ASME J. of Pres. Vessel Techn. – 1983. – Vol. 105. – Р. 153–164.
- Chaboche J.-L. A review of some plasticity and viscoplasticity constitutive theories // Int. J. of Plasticity. − 2008. – Vol. 24. − Р. 1642–1692.
- Нелинейная механика материалов / Ж. Бессон, Ж. Каето, Ж.-Л. Шабоши, Т.С. Форест. − СПб.: Изд-во Политехн. ун-та, 2010. − 397 с.
- Аверченков Е.А., Донченко А.С., Егоров В.И. О поведении материала поршня при термомеханическом нагружении // Повышение топливной экономичности и долговечности автомобильных двигателей. – М.: МАМИ, 1983. – Вып. 5. – С. 59–68.
- Дегтярев В.П. Пластичность и ползучность машиностроительных конструкций. – М.: Машиностроение, 1967. – 131 с.
- Охаси, Оно, Каваи. Оценка определяющих уравнений ползучести для нержавеющей стали 304 при повторяющемся многоосном нагружении // Теоретические основы инженерных расчетов: Труды ASME. – 1982. – Т. 104, № 3. – С. 1–8.
- Pugh C.A. Constitutive equations for creep analysis of LMFBR components // Advances in Design for Elevated Temperature Environment, ASME. – 1975. – P. 1–15.
- Малинин Н.Н., Хажинский Г.М. К построению теории ползучести с анизотропным упрочнением // Изв. АН СССР. МТТ. – 1969. – № 3. – С. 148–152.
- Миллер А. Математическая модель для монотонного и циклического изменения деформации и деформации ползучести // Теоретические основы инженерных расчетов – Труды ASME. – 1976. – № 2. – С. 1–20.
- Определяющие соотношения нестационарной ползучести при сложном напряженном состоянии / И.А. Волков, Л.А. Игумнов, Д.А. Казаков, Д.Н. Шишулин, И.В. Сметанин // Проблемы прочности и пластичности. – 2016. – Т. 78, № 4. – С. 436–451.
- Гусенков А.П. Прочность при изотермическом и неизотермическом малоцикловом нагружении. – М.: Наука, 1979. – 255 с.


