Неупругое поведение однонаправленных композитов с гексагональной структурой
Автор: А.Н. Аношкин, Макарова Е.Ю., Шардаков А.П.
Статья в выпуске: 6, 1998 года.
Бесплатный доступ
Представлена математическая модель для исследования процессов без разрушения в однонаправленных волокнистых композитах, поля напряжений и деформаций были рассчитаны методом локального приближения и FEM. Структурные диаграммы напряжений и деформаций были построены для материалов с гексагональной структурой.
Короткий адрес: https://sciup.org/146211791
IDR: 146211791 | УДК: 539.3
Текст научной статьи Неупругое поведение однонаправленных композитов с гексагональной структурой
При расчете многослойных конструкций из композиционных материалов в настоящее время широкое распространение получил подход, основанный на анализе совместной работы всего пакета разориентированных однородных трансверсально изотропных монослоев [1,2,3,4]. При этом предполагается, что необходимые характеристики монослоев могут быть получены экспериментально на основе испытания образцов из однонаправленных волокнистых композиционных материалов (ОВКМ). Поведение ОВКМ при растяжении и сжатии в направлении армирования, в поперечной плоскости, а также при сдвиге в плоскости слоя достаточно хорошо изучено экспериментально [3-8]. Однако в литературе практически отсутствуют сведения о поведении монослоя при объемном напряженном состоянии, характерном для реальных условий его работы в составе пакета. Это обстоятельство объясняется значительными трудностями при проведении подобных испытаний. Поэтому одновременно с совершенствованием экспериментальных методов активно развивается направление, связанное с разработкой математических моделей механики микронеоднородных сред, позволяющих рассчитывать эффективные свойства композитов [9,10].
При прогнозировании свойств монослоя, как правило, рассматриваются три независимые задачи: о продольном растяжении, продольном сдвиге и произвольном трансверсальном нагружении однонаправленного композита [9]. Из них задача о трансверсальном нагружении является наиболее сложной. Для её решения предложен ряд методов, при этом широкое распространение получили модели монослоя в виде среды с периодической укладкой волокон. В работах [8-12] исследуются нелинейные поля напряжений и деформаций, моделируются процессы разрушения в матрице и волокнах и рассчитываются эффективные характеристики однонаправленных композитов с тетрагональной укладкой волокон (рис. 1, а). Использование тетрагональной модели обусловлено тем обстоятельством , что в ней расстояния между волокнами при заданной объемной доле являются минимальными [9] Таким образом, можно ожидать, что прочностные свойства композита, прогнозируемые по данным моделям, являются нижними оценками реальных характеристик. Однако структура реального композита может сильно отличаться от модельных представлений. При создании конструкций из волокнистых пластиков имеет место тенденция повышения объемной доли волокон в материале. При этом геометрия структуры становится более близкой к гексагональной модели (рис. 1,6), которая обеспечивает наивысшую теоретически возможную степень укладки волокон одинакового радиуса в однонаправленном волокнистом композите. Поэтому исследование поведения композита с гексагональной структурой предел является не менее важным, чем с тетрагональной.
Рис.1. Тетрагональная (а) и гексагональная (б) модели однонаправленного волокнистого композита
Рассмотрим однонаправленный композит с периодической гексагональной укладкой цилиндрических волокон (рис. 1,6). Для расчета полей структурных напряжений и деформаций в композите используется метод локального приближения, подробно изложенный в работах [10,12,13]. В соответствии с ним для решения задачи микромеханики используется структурный фрагмент из семи ячеек, представленный на рис. 2,а.
Рис. 2 . Расчетная схема метода локального приближения для гексагональной модели ОВКМ (а) и конечноэлементная сетка фрагмента ячейки (б)

Математическая постановка задачи об обобщенной плоской деформации рассматриваемого фрагмента описывается следующей системой уравнений:
<Уи.;(г) = 0 ; £,/?) Д(и^г)ч ц./г)); Q^r) - Сйк1(?,Ф,® JJE^C?) »
С^Сеф»®Л) = С‘>,«Л)XOj(f) + C^(r); I, = пн + ст22+стзз’ (О где (у (г)и 8 СО - тензоры напряжений и деформаций. Q
(г)- тензор упругих модулей и индикаторная функция р-го структурного компонента КМ, оз (е,) - функция пластичности Ильюшина, Ф - критерий прочности для матрицы Волокна принимались упругими, изотропными и неразрушаемыми. Для описания нелинейного деформирования и разрушения матрицы использовались уравнения деформационной теории пластичности на участке активного нагружения и редуцирования жесткости в зонах разрушения,
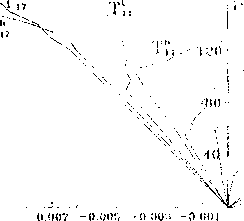
К'^.б^+С-'ф-ыСе,)^,^,,+5„6lk jS Ф > О, I, <0; (2) 0, Ф > 0, 1, > 0. Граничные условия на контуре фрагмента Q^ подбирались таким образом, чтобы напряжения, осредиенные по центральной ячейке периодичности, равнялись заданным макроскопическим S, S А (3) U .jmn V/ mn х / Начальные значения тензора А,„по можно определить из решения трех пробных задач с единичными граничными условиями, последующие значения определялись с помощью итераций [12]. Поставленная задача решалась с помощью МКЭ, на рис.2,6 приведен фрагмент используемой конечноэлементной сетки. В последующих расчётах в качестве однонаправленного волокнистого композита рассматривался эпоксидный стеклопластик. Упругие постоянные К1'* и G(i) равнялись 3236 и 1037 МПа соответственно [8] Критерий прочности эпоксидного связующего ЭД 1-10 описывался функцией Ф = р, А + р21, + pjA А + pA'I, + р512'13 + PsiAMs + p7i23 А -1, 1, = Oh , Ъ =Q„Q,j. !: П О.СУ, (4) Коэффициенты р;, рассчитанные по экспериментальным данным , приведены в работе [12] Упругие константы К121 и Сг” для стекловолокна равны 42529 и 30579 МПа соответственно [4], объемная доля волокон в композите составляла 0,58. Исследовалось 14 различных траекторий простого макроскопического нагружения в поперечной плоскости композита. Исходные значения компонент тензора макронапряжений Sy приведены в табл.1, последующие значения задавались по шагам в соответствии с условиями простого нагружения. На рис 3 представлены диаграммы /5ц/ - /£,./ и /S22/ - Е2^ для композитов с гексагональной (Ть) и тетрагональной (TJ) укладкой волокон при двухосных сжимающих нагрузках. Данные зависимости являются нелинейными, что обусловлено возникновением и развитием равновесных зон разрушения, сопротивляющихся гидростатической сжимающей нагрузке. Для траекторий ТА Т/., ТА А на диаграммах /S22/ - £22 существует точка перегиба, после которой увеличение сжимающей нагрузки S22 приводит к положительному приращению деформации Е что объясняется изменением характеристик материала матрицы в зонах разрушения и наличием большей сжимающей нагрузки Sn. Однако при гексагональной укладке волокон происходит резкое увеличение деформации, тогда как при тетрагональной -довольно плавное и с характерными ступенями. /ец*/ Рис. 3 Диаграммы деформирования однонаправленного стеклоплас гика при двухосных сжимающих нагрузках В случае гексагональной укладки волокон линейный участок на диаграммах больше, чем при тетрагональной укладке волокон, так как во втором случае разрушение начинается раньше, однако процесс разрушения в композите с гексагональной укладкой волокон происходит быстрее и завершается при более низких значениях напряжений. В табл. I, 2 приведены значения компонент тензора макронапряжений для исследованных траекторий, соответствующих началу (S^) и завершению (S^l равновесного процесса, разрушения в матрице композита с тетрагональной и гексагональной укладкой волокон. Характерные значения компонент тензора макронапряжений для композита с тетрагональной укладкой волокон, МПа Таблица 1 Траектория Исходные значения Начало разрушения Предельная нагрузка о 11 $22° С 0 012 8цМ n М 022 S12 8ИК с R 022 S,2K т2 0,0 0,0 5,0 0,0 0,0 35,0 Т4 5,0 5,0 0,0 - - 47,5 47,5 0,0 Т5 5,0 0,0 0,0 - - 37,5 0,0 о,о т7 -5,0 5,0 0,0 - -30,0 30,0 0,0 Т8 U 5,0 о,о 5,0 - 22,5 0,0 22,5 Т12 -20,0 0,0 0,0 -100,0 0,0 0,0 -105,0 0,0 0,0 т13 -40,0 -20,0 0,0 -120,0 -60,1 0,0 -210,0 -105,0 0,0 Тм -40,0 -30,0 0,0 -130,0 -97,6 0,0 -200,0 -150,0 0,0 Т15 -40,0 -10,0 0,0 -110,0 -27,5 0,0 -140,0 -35,3 0,0 {16 5,0 2,5 0,0 - - 42,5 18,7 0,0 Т17 J -40,0 -40,0 0,0 -130,0 -130,0 0,0 -160,0 -160,0 °’0 Т|8 -40,0 -5,0 0,0 -110,0 -13,8 0,0 -120,0 -15,0 0,0 1 Т19_______ 10,0 2,5 1,2 - - - 37,5 9,4 4,5 -40,0 -15,0 0,0 -110,0 -41,3 0,0 -180,0 -67,7 0,0 Таблица 2 Рис 4. Предельные кривые прочности однонаправленного стеклопластика при трансверсальных нагрузках, (а) - гексагональная модель, (б) - тетрагональная модель На рис.4 приведены предельные кривые прочности для композита с гексагональной и тетрагональной укладкой волокон. Данные кривые получены аппроксимацией расчетных точек по методу наименьших квадратов. Заштрихованная область соответствует нагрузкам, при которых в матрице возникают зоны равновесного разрушения. При расчете траекторий для оценки прочности композита принимались макроскопические напряжения, соответствующие возникновению сплошной зоны разрушения вдоль одной из сторон ячейки периодичности, либо но межфазной поверхности. При растяжении прогнозирование прочности по обеим моделям дает близкие оценки с отличием не более 5%. При сжатии в гексагональной структуре процессы разрушения начинаются при больших нагрузках, чем в тетрагональной, однако, вследствие большей однородности поля напряжений в матрице зона разрушения сразу распространяется по всей ячейке при незначительном увеличении нагрузки. Таким образом, предельная нагрузка, соответствующая исчерпанию несущей способности композита, для гексагональной модели оказывается меньше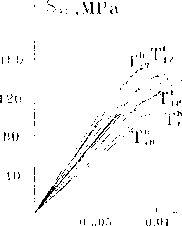
Траектория
Начало разрушения
Предельная нагрузка
с м
с М 022
S|2M
SnR
с R 022
с R 012
т2
-
о,о
0,0
32,5
т4
-
50,0
50,0
0,0
т5
0,0
0,0
0,0
40,0
0,0
о,о
т7
-
-
-37,5
37,5
0,0
т8
-
-
-
26,3
0,0
26,3
т12
-
-
-
-90,0
0,0
0,0
т13
-130,
-65,1
0,0
-149,7
-75,3
0,0
I 14
-150,0
-112,6
0,0
-169,8
-127,7
0,0
Т15
-
-
-109,9
-27,6
0,0
т16
-
-
46,3
23,1
0,0
Т17
-140,0
-140,0
0,0
-150,0
-150,0
0,0
т18
-
-100,0
-12,5
0,0
Т19
-
40,0
10,0
4,8
т23
-119,8
-45,2
0,0
-149,1
-57,2
0,2
а б


