Неупругое поведение однонаправленных композитов в условиях обобщенной плоской деформации

В настоящее время для расчета многослойных конструкций из композиционных материалов (КМ) широко используется подход, основанный на анализе совместной работы всего набора разноориентированых однородных и трансверсально изотропных монослоев, составляющих исследуемый объект[1.2,3.4]. Точность расчета напряженно-деформированного состояния и несущей способности композитных конструкций при этом во многом зависит от точности и полноты задаваемых деформативных и прочностных характеристик однонаправленных мснослоев. Предполагается, что необходимые характеристики монослоев могут быть получены при испытании образцов из однонаправленных волокнистых композиционных матер-и ал о в (ОВКМ). Экспериментальные оценки свойств ОВКМ при растяжении, сжатии в направлении армирования , в поперечной плоскости и при сдвиге в плоскости слоя приведены во многих работах, например [3-8]. Однако данные по экспериментальным исследованиям ОВКМ при различных видах плоского напряженного состояния весьма ограничены [5.7.8]. Практически полностью в литературе отсутствуют сведения о поведении монослоя при объемном напряженном состоянии, характерном для реальных условий его работы в составе композитной конструкции. Это объясняется тем, что проведение подобных испытаний сопряжено со значительными трудностями и требует уникального экспериментального оборудования. Одновременно с совершенствованием экспериментальных методов развивается направление, связанное с разработкой математических моделей механики композитов и прогнозированием на их основе эффективных свойств ОВКМ. Однако и в этом случае моделирование комбинированного нагружения монослоя приводит к значительным вычислительным трудностям, обусловленным необходимостью решения трехмерных задач МДТТ. Поэтому, как правило, для прогнозирования свойств монослоя рассматриваю гея гри независимые задачи: о продольном растяжении, продольном сдвиге и произвольном трансверсальном нагружении ОВКМ с модельной структурой [9]. Таким образом, проблема исследования поведения монослоя при комбинированных условиях продольного и поперечного нагружения по-прежнему остается актуальной.

В настоящей работе предложена нелинейная математическая модель ОВКМ. учитывающая совместное влияние различных условий трансверсального нагружения и постоянной продольной деформации. Рассматривается однонаправленный композит с периодической тетрагональной укладкой цилиндрических волокон. Для расчета полей напряжений и деформаций в компонентах композита используется метод локального приближения, подробно рассмотренный в работах [10,11,12]. В соответствии с ним для решения задачи микромеханики используется структурный фрагмент, представленный на рис. 1.

Рис.1 Расчетная схема метода локального приближения(а.Ь) и диаграмма деформирования связующего ЭДТ-10 (с)

Математическая постановка задачи об обобщенной плоской деформации рассматриваемого фрагмента описывается следующей системой уравнений /

Оу)(г)=0  б9(» )='"(км(г )+и1>!(г»; а9(г )=с9м(г,ф,«>,1, )см(г ) ;

СуыСг.Ф^,!! )= C^CMJ, ^'^^^^^^(г);

где a(r )w к (г ) - тензоры напряжений и деформаций, С^<р> и Х^<рЧг )- тензор упругих модулей и индикаторная функция р-го структурного компонента КМ.

«(в,)- функция пластичности Ильюшина, Ф - критерий прочности для матрицы.

Волокна принимались упругими, изотропными и неразрушаемыми. Для описания нелинейного деформирования и разрушения матрицы использовались уравнения деформационной теории пластичности на участке активного нагружения и редуцирования жесткости в зонах разрушения

к(,,8узы +^'41-

К(%8М,  Ф>0,

^(Ф^Л ) =

^m^ Ж_к8_у1 + ⁵il‘⁵jk ^-^⁵ij⁶kl А

О, Ф>0,  it>0.

Приведенные соотношения отражают два возможных механизма поведения матрицы в разрушенных зонах: полная потеря несущей способности при I, >0ч способность воспринимать только сжимающую нагрузку в области 1,<0.

Функцию пластичности Ильюшина «(eJ строили на основе кривой о.-е, .На межфазной поверхности задавали условия полной адгезии. Граничные условия на контуре фрагмента подбирали таким образом, чтобы напряжения, осредненные по центральней периодической ячейке, равнялись заданным макроскопическим Г [10.11,12]

В отличие от проведенных ранее исследований [11,12] в настоящей работе компонента деформации ^принимала заранее заданное ненулевое значение, что соответствующим образом учитывалось в определяющих соотношения (2) Поставленная задача решалась с помощью МКЭ. Известная схема метода [13]. используемая в случае плоского деформируемого состояния, модифицировалось следующим образом. Для связи напряжений и деформаций в конечном элементе использовалось уравнение

(а}= f DДг^ + ^d ^е,₃ , {оД = {<т_)г,а₂₂,<т₎₂ }, е = U_H,s₂2.^ei2} •            (-')

здесь [D]- матрица жесткости при ИДС. {d}- вектор дополнительных жесткостей, учитывающий влияние продольной деформации £„. Компоненты матрицы [D] и вектора {d} вычисляются через технические упругие константы с помощью соотношений, приведенных в общем случае для ортотропного материала в работе [14]. Второе слагаемое соотношений (4) эквивалентно действию фиктивных начальных напряжений taV =Ц<Цеи-                                              (4)

Дальнейший учет влияния продольной деформации осуществлялся посредством добавления к правой части глобальной системы уравнений слагаемого

^У^ЧВПоУ^,                         (5)

где t и А - толщина и площадь элемента. [В]т - транспонированная матрица градиентов функций формы.

В соответствии с постановкой задачи, соотношения (2) являются нелинейными. Линеаризация уравнений деформационной теории пластичности осуществлялась методом начальных деформаций, для учета редуцирования жесткости в разрушенных зонах использовался метод начальных напряжений [13].

В последующих расчётах в качестве ОВКМ рассматривался эпоксидный стеклоластик. Диаграмма деформирования эпоксидного связующего ЭДТ-10. полученная на основе обработки экспериментальных данных [15]. приведена на рис 1.с. Упругие постоянные К111 и G*1’равнялись 3236 и 1037 МПа соответственно [15]. Критерий прочности ЭДТ-10 описывался функцией ф = pjV2 +р2г. +рУ2'/2^2+рУ2‘^+рУ~2^2 + pjyni,i3 +р-123,2С " I

^!1=Ои • h = ".j^i, • h =O₁₅CTjk«ik-                                  (6)

Коэффициенты р,, рассчитанные по экспериментальным данным [15]. приведены в работе [11]. Упругие константы К^'и G<2' для стекловолокна были равны 42529 и 30579 МПа соответственно [4], объемная доля волокон в композите составляла 0.58.

Исследовалось 14 траекторий трансверсального нагружения при следующих значениях продольной деформации е33"0.600: 0.015: 0.020. Компоненты sh тензора макронапряжений задавались формулами s^1 = х^41 А-а к). к=0,1,2,..л..

s^s^fl+az+pfk-z)) , k=z+l,z+2,...Z.

От начального уровня s^* до некоторого значения s^¹, предшествующего первому акту разрушения, нагружение происходило с крупным шагом сс. далее до заключительной точки траектории s^^z> - с мелким шагом Р. Начальные значения компонент тензора макронапряжений приведены в табл.1.

Таблица 1

Параметры исследованых траекторий нагружения
Траектория	(Su"". S22"”. Si2<°>), Мпа	£зз|РА %	S33<R». МПа
Т;	( 0.0, 0.0, 5.0)	2.50	1604
Т4	( 5.0, 5.0, 0.0)	2.25	1447
Т5	( 5.0, 0.0, 0.0)	2.25	1447
Т7	( -5.0, 5.0, 0.0)	2.25	1447
т8	( 5.0, 0.0, 5.0)	2.25	1447
Т,2	(-20.0, 0.0, 0.0)	2.25	1450
Т,3	(-40.0,-20.0, 0.0)	2.70	1731
Т14	(-40.0,-30.0, 0.0)	2.70	1731
Т15	(-40.0.-10.0, 0.0)	2.70	1731
Т16	( 5.0, 2.5, 0.0)	2.25	1450
т17	(-40.0, -40.0, 0.0)	3.00	1917
Т,8	(-40.0, -5.0, 0.0)	2.70	1728
Т„	( 10.0, 2.5, 1.2)	2.25	1447
Т23	(-40.0,-15.0,0.0)	2.70	1730

На рис.2-4 приведены диаграммы s^ - е~ , полученные для различных е33*. а также фрагменты, иллюстрирующие развитие зон нелинейного деформирования и разрушения. В данной системе обозначений белыми полями отмечены зоны упругого деформирования, области одинарной и двойной штриховки соответствуют зонам нелинейного деформирования матрицы при 35 МПа<а,< 56 МПа и 56 МПа < а,, соответственно, зоны разрушения при I, > 0 отмечены точками, а при I, <0 -зачернены. Анализируя рис.2-4, можно отметить, что при растягивающих нагрузках зависимости $п-£^ линейны (см. рис.2,3.4. d). а при двухосных сжимающих нагрузках - нелинейны (см. рис.2.3.4, а.Ь). Это объясняется, главным образом, появлением и развитием равновесных зон разрушения, сопротивляющихся гидростатической сжимающей нагрузке. В последнем случае для траекторий Тц.Тзз ,Ты на диаграммах s22 - с^ наблюдается точка перегиба, после чего увеличению сжимающей нагрузки s22 соответствует уже положительное приращение деформации £22, что объясняется изменением характеристик материала матрицы в зонах разрушения и наличием большей сжимающей нагрузки s/;. При ненулевых значениях продольной деформации £33 диаграммы ’^-^ получают смещения по оси £g , обусловленные наличием соответствующей поперечной деформации от макронапряжений s33. По мере увеличения £33 зоны пластичности появляются раньше, однако это практически нс влияет на наклон диаграмм деформирования композита вследствие слабо выраженной нелинейности деформирования связующего ЭДТ-10 (см. рис.1 ,с).

Прочность композита при рассмотренных траекториях нагружения, как и в работе [12]. оценивалась по условию образования в ячейке непрерывного кластера разрушенных зон, пересекающих ячейку либо вдоль одной из сторон, либо по межфазной поверхности. Развитие зон разрушений, как правило, происходило лавинообразно при растягивающих нагрузках и равновесным образом при двухосных сжимающих нагрузках. Таким образом, для траекторий нагружения ТА. Ты, ТА. ТА. Тзз, Т>7 наблюдались стабильные процессы развития зон разрушения в матрице. С увеличением g равновесные зоны разрушения возникают при более ранних нагрузках. На рис.5 приведены предельные кривые, аппроксимирующие по методу наименьших квадратов расчетные точки, соответствующие потере прочности ОВКМ при трансверсальных нагрузках с различной продольной деформацией. Заштрихованная область соответствует нагрузкам, при которых в матрице возникают равновесные зоны разрушения. Видно, что наличие продольной деформации мало влияет на прочность композита при трансверсальном сжатии, однако существенно снижает прочность при трансверсальном растяжении. Для сравнения на рис.5 показаны интервалы экспериментальных оценок прочности однонаправленного стеклопластика при поперечном растяжении и сжатии [4-8]. В расчетах для каждой траектории нагружения удалось подобрать такое значение е*_и, при котором разрушение материала начинается, практически при любых начальных значениях тензора макронапряжений s# . Найденные таким образом предельные деформации е,,¹ и соответствующие им напряжения s™' приведены в табл.1, эти оценки соответствуют экспериментальным значениям прочности стеклопластика при продольном растяжении . приведенным в литературе: <г^ = 1195 МПа. сг*₃ =0.0239 [7]; <7^ = 1200 МПа [8]; <7.^ = 1600 МПа[4].

Заключение

Рассмотренная математическая модель позволяет исследовать процессы нелинейного деформирования и разрушения в структуре однонаправленных волокнистых композитов при совместном действии продольных и поперечных нагрузок. На основе данной модели возможно прогнозирование нелинейных деформационных и прочностных характеристик монослоя при произвольной комбинации таких нагрузок. Проведенные расчеты показали, что продольное растяжение значительно снижает прочность ОВКМ при трансверсальном растяжении и слабо влияет на прочностные характеристики при поперечных сжимающих нагрузках.

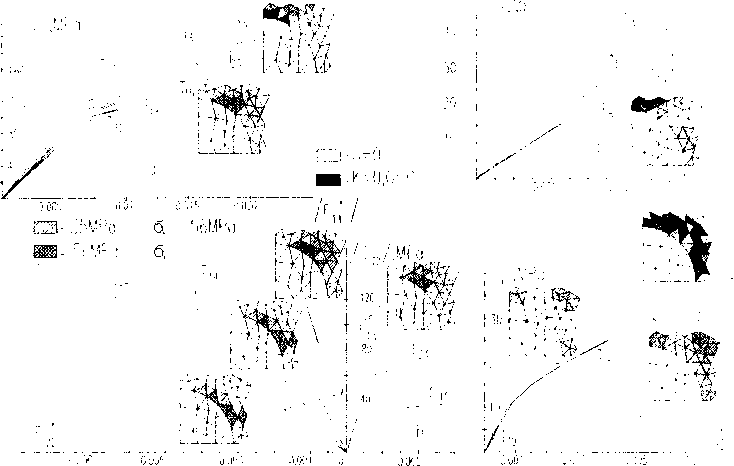
Рис.2 Диаграммы деформирования однонаправленного стеклопластика при трансверсальных траекториях нагружения. езз⁼0.000

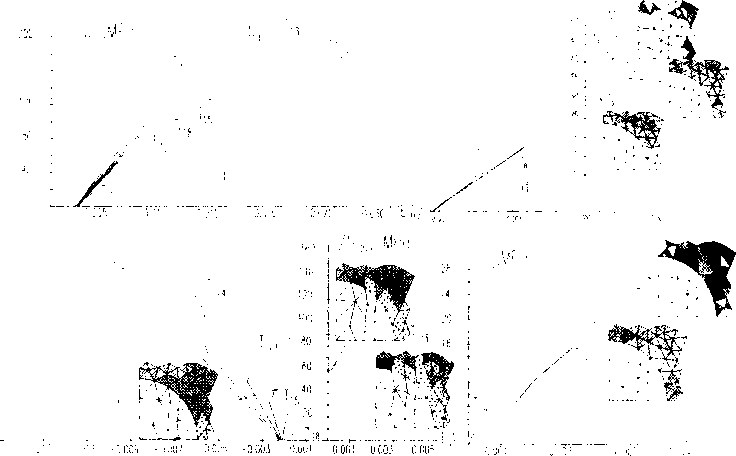
Рис.З Диаграммы деформирования однонаправленного стеклопластика при трансверсальных траекториях нагружения, кзз—0.015

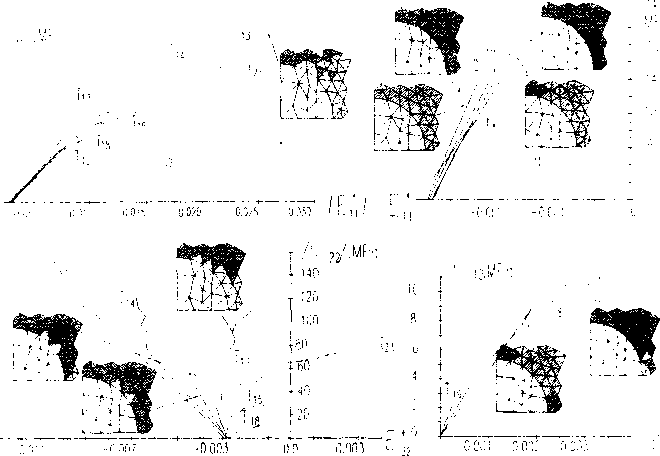
Рис.4 Диаграммы деформирования однонаправленного стеклопластика при трансверсальных траекториях нагружения, 8зз=0.020

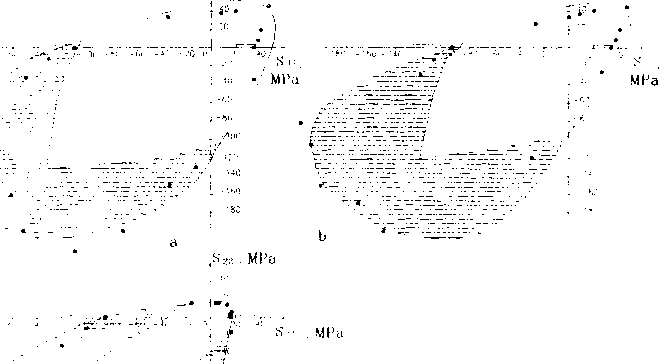
Рис.5. Предельные кривые прочности однонаправленного стеклопластика при трансверсальных нагрузках : езз-0.000 (а), Езз=0.015 (Ь), £зз⁼0.020 (с)