Неустойчивость скользящего контакта с покрытием на упругой подложке при наличии трения и разогрева от трения
Автор: Зеленцов Владимир Борисович, Митрин Борис Игоревич, Айзикович Сергей Михайлович
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Механика
Статья в выпуске: 4 (87) т.16, 2016 года.
Бесплатный доступ
Рассматривается нестационарная динамическая контактная задача термоупругости о скольжении с трением и разогревом от трения жёсткой полуплоскости по поверхности упругого покрытия, сцепленного с упругой подложкой из другого материала. Решение сформулированной начально-краевой задачи записывается в виде контурных интегралов обратного преобразования Лапласа. После изучения изолированных особых точек подынтегральных функций в комплексной плоскости переменной интегрирования решение задачи строится в виде бесконечных рядов по полюсам с добавлением интегралов по берегам разреза. Определяются границы областей устойчивых и неустойчивых решений задачи на множестве её безразмерных параметров. Изучается влияние упругости подложки на границу области неустойчивых решений задачи, а также на развитие температуры и напряжений на скользящем термофрикционном контакте.
Скольжение, контакт, трение, фрикционный разогрев, упругая подложка, динамика, термоупругая неустойчивость
Короткий адрес: https://sciup.org/14250248
IDR: 14250248 | УДК: 539.3 | DOI: 10.12737/22148
Текст научной статьи Неустойчивость скользящего контакта с покрытием на упругой подложке при наличии трения и разогрева от трения
Введение. Для защиты рабочих поверхностей деталей механизмов и машин широко применяются защитные покрытия — антифрикционные, антикоррозийные, противоизносные и другие. Замечено, что при увеличении скорости функционирования механизмов и машин на скользящем контакте их поверхностей достаточно часто возникает неконтролируемый рост температур и давлений, который может привести к возникновению нештатных ситуаций, предаварийному и аварийному состоянию оборудования. В связи с этим изучение скользящего контакта рабочих поверхностей при наличии покрытий представляет как теоретический, так и практический интерес. Математическому моделированию и решению задач о скользящем контакте с учетом сил трения и разогрева от трения уделялось достаточно много внимания [1–17]. Для определения области неустойчивых решений контактной задачи — области термоупругой неустойчивости (ТУН) скользящего контакта часто применяется метод малых возмущений [1– 8], а для определения решения задач — численные методы [9, 10]. Метод интегрального преобразования Лапласа оказался наиболее универсальным методом аналитического решения задач этого класса [11–17], который не только позволяет построить точное решение задачи, но и определить область устойчивых решений задачи, совпадающую с областью ТУН скользящего контакта. В [1–5, 11–13] исследовались области устойчивых решений квазистатических задач термоупругости о скользящем контакте, а в [6, 7, 14, 17] было показано, что область устойчивых решений динамических задач является подобластью области устойчивых решений квазистатических задач. В настоящем исследовании изучается влияние упругих свойств подложки покрытия на динамику контактных напряжений и температуры при скольжении жёсткой полуплоскости по поверхности покрытия.
Постановка задачи. Рассматривается динамическая задача термоупругости в рамках плоской деформации о скольжении с постоянной скоростью V жесткой полуплоскости I (h ≤ x < ∞) по поверхности x = h упругого покрытия (0 ≤ x ≤ h) , нижняя грань x = 0 которого сцеплена с подложкой (основанием) в виде упругой полуплоскости II (-∞ < x ≤ 0) из другого материала (рис. 1). Скольжение недеформируемой полуплоскости I по поверхности упругого покрытия происходит с учетом кулоновского трения и разогрева от трения. В начальный период времени полуплоскость I деформирует упругое покрытие, смещаясь вдоль вертикали в направлении, противоположном оси x, по закону ∆(t) . Движущаяся полуплоскость I теплоизолирована, а поток тепла, образующийся за счет трения, направлен в упругое покрытие. Кроме того, на границе покрытия и полуплоскости II выполняются условия идеального теплового контакта. Начальная температура полуплоскости II, как и покрытия, равна нулю. В начальный момент покрытие и полуплоскость II находятся в покое. На бесконечности (x → -∞) в полуплоскости II смещения и напряжения исчезают.
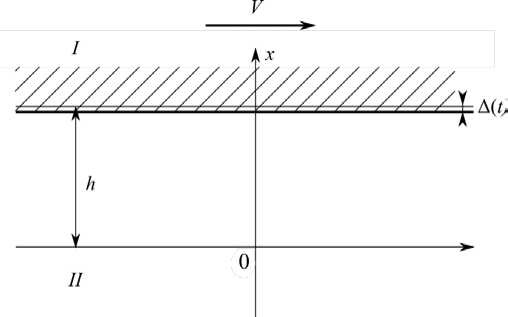
Рис. 1. К постановке задачи термоупругости о скользящем термофрикционном контакте
Представленная задача сводится к решению дифференциальных уравнений термоупругости для покрытия (0 < x < h ) и подложки ( -∞ < x < 0) совместно с уравнениями теплопроводности:
∂ 2 u 1 ∂ 2 u
-
∂ x a ∂ t
1 + ν ∂ T
= α ,0 < x < h , t > 0
1 - ν ∂ x
∂ 2 T 1 ∂ T
-
∂ x 2 κ ∂ t
= 0, 0 < x < h , t > 0
∂ 2 u 1 1 ∂ 2 u 1
-
∂ x a 1 ∂ t
1 + v ∂ T
1 α 1 1
1 - v 1 ∂ x
-∞ < x < 0 , t > 0
∂ 2 T 1 - 1 ∂ T 1 = 0 ∂ x 2 κ 1 ∂ t
-∞ < x < 0 , t > 0
2 µ (1 -ν ) ρ (1 - 2 ν ) ,
a 1 =
2 µ 1 (1 -ν 1 )
ρ 1 (1 - 2 ν 1 )
(0.1)
(0.2)
(0.3)
(0.4)
(0.5)
где µ — модуль сдвига, ρ — плотность, ν — коэффициент Пуассона, α — коэффициент линейного теплового расширения, κ — коэффициент температуропроводности, a — скорость продольной упругой волны, u ( x , t ) , T ( x , t ) — функции распределения смещений и температуры в покрытии (без индекса). Индексом 1 отмечены соответствующие параметры µ 1 , ρ 1 , v 1 , α 1 , κ 1 , a 1 , u 1( x , t ) , T 1( x , t ) подложки.
Граничные условия для дифференциальных уравнений (0.1), (0.2) на верхней поверхности покрытия x = h принимаются в форме:
механическое:
u ( h , t ) = -∆ ( t ) t > 0
(0.6)
температурное: K ^(^’ t ) =- fV с ( h , t ) t > 0 (0.7)
d x
Условие (0.7) означает, что величина потока тепла в покрытие пропорциональна работе сил трения на контакте V т , где т = f с ( h , t ) — касательные напряжения на поверхности покрытия, А ( t ) — закон внедрения, K — коэффициент теплопроводности материала упругого покрытия, f — коэффициент трения, с ( x , t ) — нормальные напряжения в покрытии.
На нижней поверхности x = 0 покрытия выполняются механические условия сцепления покрытия с упругой полуплоскостью II и температурные условия их идеального теплового контакта механические: и(0,t) = и1(0,t) c(0,t) = <^(0,t) t > 0(0.8)
температурные: T(0, t) = T1 (0, t) K ^(^ t) = K1 (^ t) t > 0(0.9)
dx где K1 — коэффициент теплопроводности материала полуплоскости II,
C ( x , t ) — нормальные напряжения в полуплоскости II .
На бесконечности в упругой полуплоскости II смещения и1 (x, t) и напряжения c1 (x, t) исчезают, также как и температура, то есть выполняются условия механические: и 1(-«, t) = 0, C1(-», t) = 0, t > 0 (0.10)
температурные: T1( -« , t ) = 0 t > 0 (0.11)
Связь между напряжениями, смещениями и температурой в покрытии и подложке определяется соотношениями Дюамеля-Неймана [18]
C x,t ) = М-Й. * - М+Й a T ( x , t ) (0.12)
1 - 2 v 8 x 1 - 2 v
d( x , t ) = Y1 " V 1) - Y1 + V 1) a T 1 ( x , t ) (0.13)
1 2 V 1 d x 1 2 V 1
Начальные условия задачи на смещения, их скорости и температура нулевые:
и ( x ,0) = ^I x 0. = и ( x ,0) = d u 1( x ,0) = T ( x ,0) = T ( x ,0) = 0, А (0) = 0 (0.14)
8 1 1 8 1 1
Закон внедрения полуплоскости I в поверхность покрытия А ( t ) имеет активную фазу внедрения на 0 < t < t £ и пассивную на t £ < t < « и принимается в виде
А ( t ) = А 0 [( - 1 + e s t ) H ( t ) H ( t £ - 1 ) + H ( t - 1 £ )] (0.15)
где А 0 , 0 < А 0 < h — глубина максимального внедрения жесткой полуплоскости I в упругое покрытие, t £ = s 1 ln2 ( s > 0) — время активной фазы внедрения, s — параметр закона внедрения, H ( t ) — функция Хэвисайда.
Таким образом, решение рассматриваемой нестационарной динамической контактной задачи термоупругости о скольжении с учетом трения и разогрева от трения жёсткой полуплоскости I по поверхности покрытия на упругой подложке в виде полуплоскости II сводится к совместному решению дифференциальных уравнений термоупругости (0.1), (0.3) совместно с уравнениями теплопроводности (0.2), (0.4) с граничными условиями (0.6) -(0.9), условиями на бесконечности (0.10) -(0.11) и начальными условиями (0.14).
Решение задачи в контурных квадратурах. Применив преобразование Лапласа к дифференциальным уравнениям (0.1) -(0.4) с учётом начальных условий (0.14), к формулам Дюамеля-Неймана (0.12) -(0.13) и граничным условиям (0.6) -(0.9), получим систему четырёх линейных обыкновенных дифференциальных уравнений второго порядка с постоянными коэффициентами относительно трансформант Лапласа искомых функций и ( x , t ), T ( x , t ). После решения системы дифференциальных уравнений относительно трансформант с учётом граничных (0.6) -(0.9) условий в трансформантах и условий на бесконечности (0.10) -(0.11) и применения к ним обратного преобразования Лапласа, получим решение задачи в виде контурных квадратур [19]
7 ~
T ( x , t ) =---- 1--L j o ( z ) NT ( x , z ) R -1 ( z ) ezt dz t > 0, 0 < x < h
1 + v a h 2 n i Г
N T ( x , z ) = V z to ( z ) to 1 ( z ) ( a * ch y z + Ц * sh y z ) x
х
R ( z ) = ( a * sh y z + Ц * ch y z ) to 1 ( z ) Q 1 ( z ) - Y V Q 2( z )
Q 2 ( z ) = —a*^*= ю ( z ) Ю 1 ( z ) + Ю 1 v * a * к *
I х
(0.1)
(0.2)
(0.3)
х
a
to ( z ) = 1 - Y 2 z ,
to 1 ( z ) = 1 -y j 2 к * z ,
a
a * = — , a * = — , к *
a i
a 1
к к
—, Y 1 = —г, Y = к /( ah ), V = a 1 h
к 1
fV a 2 ц (1 + v ) h K 1 - 2 v
_ 2ц (1 - v )/(1 - 2 v ) Ц * = 2 ^ 1 (1 - V 1 )/(1 - 2 V 1 )
, *
_ (1 + v )/(1 - v ) к
= , K = , I
(1 + v 1 )/(1 - v 1 ) K 1 к
h 2
~
t
—, t = —
к
t к
g ( x , t ) = -
2^М — ■ ( z ) (1 - 2 v ) h 2 n i Г ' '
N “ ( x ’ z ) ez7dz R ( z )
0 < x < h , t > 0
0 2 -
N a ( x , z ) = Y z ® 1 ( z ) Z G k ( x , z ) + to, ( z ) G 3 ( x , z )
(0.4)
(0.5)
G 1 ( x , z ) = -y 2 V^z ( a * ch G 2 ( x , z ) = ( a * ch ( y zxh - 1 )
+ Y 2 V 4z Цк*;
I + K * ch ( y[zxh 1 ))
l+
G з ( x , z ) = y V 7
aK
------;= to( z ) + ( YЦ * K * V z v * a *A /к*
—
где Г = { z : - i м + dt к , i м + dt к} — контур интегрирования в комплексной плоскости z, который представляет собой прямую линию, параллельную мнимой оси и отнесенную от нее вправо на величину dt к , в которой d подбирается таким образом, чтобы все полюсы подынтегральных функций в (0.1), (0.4) были бы левее dt к . Функция D ( z ) определяется через трансформанту Лапласа закона внедрения (0.15) и имеет вид
D ( z ) = А 0
2 e - z t вк - 1 1 - e - (z -е t к ) t Ек
--1-- z z -81
к
Re z > e t t к вк
t 8 t к
(0.6)
Исследование подынтегральных функций контурных квадратур в (2.1) и (2.4) показывает, что
D ( z ) N T ( x , z ) R -1( z ) = O ( z - 1/2) при | z | ^»
D ( z ) N a ( x , z ) R -1( z ) = O (1) при | z | ^ м (0.7)
Это означает, что интеграл в (0.4) понимается в обобщенном смысле [20, 21] и для получения его регулярной части необходима регуляризация подынтегральной функции на бесконечности при | z | ^ м . Регуляризация подынтегральной функции в (0.4) производится с помощью выражения
D ( z ) ( ch y zxh - 1 + ( ц * / a * ) sh y zxh 1 )( sh y z + ( ц * / a * ) ch y z ) 1 Y z (0.8)
после чего формула (0.4) для g ( x , t ) принимает вид
g ( x , t )
2 ц (1 - v ) (1 - 2 v ) h
Q ( x , t ) + 1— J D ( z ) 2 n i г
N а ( x , z ) R . ( z )
~ e z dz
0 < x < h , t > 0
(0.9)
Q ( % , t ) = A 0 - 1 t a [ “ z h ] qn [ a ( to - ( % , t ) ) + q A ( to + ( % , t ) ) ] (0.10)
n = 1
to ± ( % , t ) = a - 1 [ at - (2 n - 1) h ± % ]
N a ( % , z ) = N 0 ( % , z ) | sh y z + — ch у z l-y zR ( z ) | ch | у z — ] + — sh | у z — | l (0.11)
( a * J ( ( h J a * ( h ))
R o ( z ) = f sh y z + — ch y z J R ( z ), q = 1 Ц ** (0.12)
( a * J 1 + ц */ a *
Изолированные особые точки подынтегральных функций квадратур решения. Подынтегральные функции полученных квадратур (0.1), (0.9) удовлетворяют лемме Жордана-Гаусса [19], так как имеют алгебраическое убывание на бесконечности. Кроме того, подынтегральные функции в (0.1), (0.9) являются многозначными с точкой ветвления алгебраического типа z = 0. Для получения области однозначного представления подынтегральных функций в комплексной плоскости переменной интегрирования z = ^ + i n проводится разрез от точки z = 0 до точки z = -да вдоль отрицательной части действительной оси. Для вычисления квадратур методами теории функций комплексного переменного необходимо изучение всех изолированных особых точек в комплексной плоскости интегрирования. Полюсы и устранимые особые точки, если такие есть, определяются из трансцендентного уравнения
R ( z ) = 0 (0.1)
где R(z) определена в (0.3). При определении нулей R(z) численными методами в комплексной плоскости z = ^ + in необходимо хорошее нулевое приближение. Анализ уравнения (0.1) производится с помощью содержащихся в R(z) основных безразмерных параметров y и V . При произвольном y , положив V = 0, из (0.1) получим упрощенное уравнение to(z)to1(z)Q0(z)Q[ (z) = 0, (0.2)
где Q 0 ( z ) = a * sh y z + Ц * ch y z , Q [ ( z ) = д/к Т ch V z " + K * sh V z .
Нулями to ( z ) и to [ ( z ) в (0.2), а значит и в (0.1) при V = 0 являются z = Y 2 и z = Y - 2 к- 1 соответственно, которые, однако, не являются полюсами подынтегральных функций, а являются устранимыми особыми точками, так как являются нулями числителей — функций N T ( % , z ) (0.2), N a ( % , z ) (0.11).
Комплексные корни уравнения Q 0 ( z ) = 0 определяются формулой
± 1 1л n / Y q > 0 1 -ц* / a
(0.3)
z 0 n = nln q I ± i ) q = ——, n = 0,1,2, -
2 y [п ( n + 1)2 ) / y q < 0 1 + ц * / a *
и так как 0 < | q | < 1, то z ± n располагаются в комплексной плоскости слева от мнимой оси, а при q = 1 — на мнимой оси.
При решении уравнения Q[ (z) = 0 в комплексной плоскости z с разрезом вдоль отрицательной части действительной оси arg(z) на верхнем листе римановой поверхности изменяется от -п до п : -п < arg(z) < п. На промежуточном этапе решения получается равенство zk
= ^ ^| + i п
к Х> 0
к + 1)2 Х< 0
1 -^/К Т / K *
1 +VK 7 / к * ’
к = 0, ± 1, ± 2, _
(0.4)
при этом Rei
; (^ ) = "2 ln| Х| < 0 при д/К 7 / K * < 1, а Re (V z ) = ln| Х| > 0
ни при каких ^К 7 / K * . Таким образом, V z имеет
Re (V z ) < 0
и находится во 2-ом квадранте с
п /2 < arg
(V z )
< п
или в 3-ем квадранте с
—
п < arg
(v z )
<-п /2. При
возведении в квадрат Vz его arg(z) должен увеличиться в 2 раза, после чего z попадает на другой лист римановой поверхности с п< arg(z) < 2п или с -2п < arg(z) <-п . Ветвь Vz выбирается на верхнем листе выполнением равенства V1 = 1. Отсюда следует, что уравнение Q[ (z) = 0 на верхнем листе римановой поверхности корней не имеет.
Таким образом, z ± n являются нулевыми приближениями для определения множества нулей z n (V) V е [0, да )
при фиксированных значениях у при численном решении уравнения (0.1). При V > 0 на верхнем листе римановой поверхности присутствуют также множества нулей Z.(V) к = 0,1,2,... , V е [Vк, Vk“], где V^, V- — значения V , при котором Z.(V) выходят с нижнего листа римановой поверхности на верхний лист (+) и обратно (-) (при фиксированных остальных параметрах уравнения).
Исходя из физического смысла величин к, a, h, параметр у = к (ah)-1 может принимать только положительные действительные значения. Отношение к/а имеет размерность длины и для большинства материалов составляет величину порядка 1-30 нм. Поэтому практический интерес представляют значения 0 < у < 1.
Расположение нулей функции R(z) (0.3) при V е [0, да) и фиксированном у = 10 2 иллюстрирует рис. 2. Цвет траектории отражает значение ц*, которому соответствует траектория (значения приведены на рисунке). Множества z± (V) n = 1, 2, 3 представляются траекториями, похожими на незаконченные эллипсы (рис. 2). Начальные точки траектории z±n = z± (0) определяются формулой (0.3). Стрелки на траекториях показывают направление перемещения mzn (V) по траектории при изменении V от 0 до да и указывают на точку сгущения, к которой стремится z± (V) n = 1, 2, 3 при V ^да. При увеличении ц*, что соответствует уменьшению жесткости подложки относительно покрытия, z±n перемещаются влево, а вместе с ними смещаются и множества z± (V), что приводит к увеличению величины V, при которой zn (V) приобретает положительную действительную часть. Следует отметить, что множества z± начинаются слева от мнимой оси, а заканчиваются в точке сгущения ck. = lim z± (V) справа (ц* = 10-5) V ^да или слева (ц* = 1, 2,1, 2,3). Дальнейшее увеличение ц* приводит к тому, что траектории нулей z± (V) оказываются полностью в левой полуплоскости, и Re(z± (V^)) < 0 при любых значениях V е [0, да).
м!т(.-)
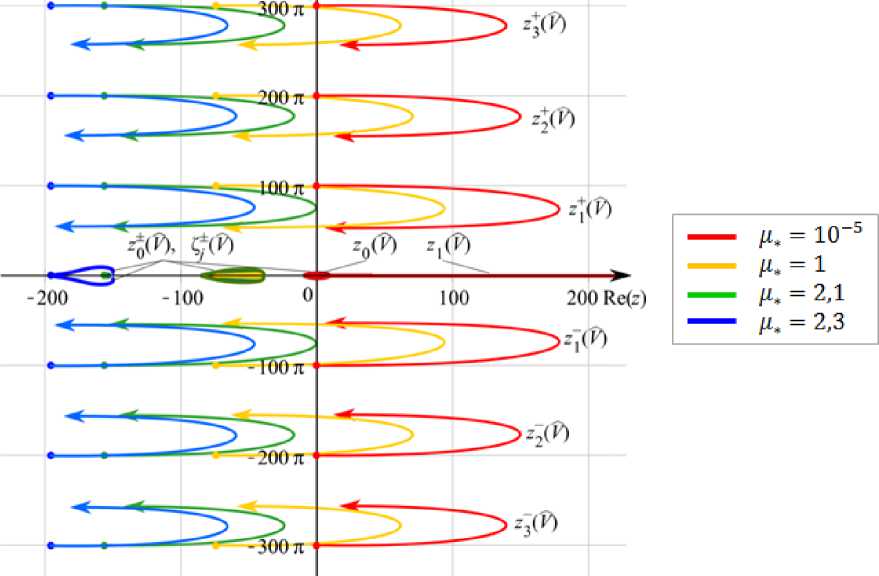
Рис. 2. Расположение нулей функции R ( z ) (0.3) в комплексной плоскости при V е [0, да ) и различных значениях ц * (обозначены цветом)
Пары нулей z + (V) = zq (V) располагаются вблизи действительной оси и при изменении V от 0 до 7 сначала отдаляются от нее, находясь слева от мнимой оси, затем пересекают мнимую ось, после чего вновь приближаются к действительной оси уже справа от мнимой оси и при некотором V переходят на действительную ось, превращаясь в нули zq (V) и z 1 (V). Первый из них при дальнейшем увеличении V устремляется по действительной оси в точку ветвления, располагающуюся в начале координат, и покидает верхний лист римановой поверхности, в то время как второй устремляется по действительной оси в положительном направлении. При этом, чем значение ц* ближе к 0, тем более «стянутой» к началу координат оказывается вся траектория zQ(V') . Таким образом, после того, как z±(V) в первый раз пересекает действительную ось, в правой полуплоскости всегда присутствует нуль, являющийся полюсом подынтегральных функций в (Q.1), (Q.9) для T(x, t), g(x, t).
Заметим, что для zn и Z ± выполняются соотношения сопряженности z„+= z„ , Z +=Zk n,k = Q,1,2,_ (Q.5)
Таким образом, нули характеристического уравнения или определителя системы (q.1), с одной стороны, являются собственными значениями начально-краевой задачи (Q.1) -(Q.14), а с другой — полюсами подынтегральных функций контурных квадратур решения задачи в (Q.1), (Q.9).
Решение задачи. Полученные сведения об изолированных особых точках подынтегральных функций в (Q.1), (Q.9) позволяют вычислить эти интегралы методами теории функций комплексного переменного [22] и представить решения задачи — температуру и напряжения в виде функциональных рядов по полюсам подынтегральных функций и несобственных интегралов по берегам разреза
Z 2
T ( x , t ) = 1--- ^V A Q I Sk ( x , ~ ) H ( ( - 1) k ( ~ - t EK ) ) Q < x < h , t > Q
(Q.1)
1 + v a h k = 1
c ( x , t ) = -
1^^ A Q Q ( x , t ) + I S k ( x ,~ ) H ( ( - 1) k ( ~ - t (1 - 2 v ) h L k = 1
k = 1
1Ек ) ) Q < x < h , t > Q
~ в которых t , Q(x, t) из (Q.3), (Q.1Q). Функции Sk (x, t) k = 1,2 вычисляются по формулам
S 1 ( x , t ) = G ( x , t ) + 5 1 ( x , t ), S 2 ( x , t ) = G ( x , t ) - 2 G ( x , t - 1 eK ) + 5 2 ( x , t )
G(x, t) = I [g- (z+ )K‘(z+, x, t)+ 0- (zk )K‘(zk, x, t)]+ k=Q
+ I [ g- ( z + ) k ‘ ( z + , x , t ) +g- ( z k ) K ‘ ( z - , x , t ) ]
k = Q
5 1( x , t ) = K ( e t K , x , t ) - K (Q, x ,Q) + J 1( x , t ), 5 2( x , t ) = K (Q, x ,Q) + J 2( x , t )
1 7 + N ( x , - i ^ , -9 N ( x , i V^ , -^ )
J ( x , t ) , 'g ©Q ( x , ^ ) d ^ , Q ( x , ^ ) = —T—/=— X— T1V —T
2 n i q R ( - i Д , -Z ) R ( i ТЁ , -Z )
(Q.2)
(Q.3)
(Q.4)
(Q.5)
N ( x , z ) / x
=-------- exp( zt )
R '( z )
e t к z ( z ±e t к )
K ( z , x , t ) = N ( x ’ z ) exp( zt ), K '( z , x , t ) = R ( z )
K (Q, x ,Q) = lim N ( x ’ z ) , G ± ( z ) = - z ^ Q R ( z ) :
В формулах (Q.5) введены обозначения
N ( x , z ) = N ( x , V z , z ) , R ( z ) = R (V z , z ) для отслеживания поведения этих функций на берегах разреза.
Области устойчивых и неустойчивых решений. Функция G ( x , t ) (Q.4) из Sk ( x , t ) (Q.3) содержит два бесконечных ряда — по z + и по Z +
G ( x , t ) = S + ( x , t ) + S - ( x , t )
(Q.1)
S + (x,t) = Ib(x,zk^ezt, S-(x,t) = Ib(x,Z +)eZ+t k =1 k =Q
N ( x , z ) ‘ ( x , z ) = 0 ( z ) —
Если все Re ( z +)< 0 и Re ( z + ) < 0 n , к = 0,1,2, . для 0 < V < V 0 , то есть все z + и Z + находятся левее мнимой оси рис. 2, а при V > V 0 хотя бы один из них - z + * или Z + * — находится справа - Re ( z + * ) > 0 или Re ( z + * ) > 0 , то область V S е [ 0, V 0 ] при фиксированных других параметрах ц * , у , a * , . называется областью устойчивых решений задачи, а V U е V 0 , да ) называется областью неустойчивых решений задачи. Если у одного из полюсов z + * (или Z + * ) Re ( z + * ) > 0 или Re ( z+ * ) > 0, то один из рядов в (0.1) становится расходящимся, а решение его содержащее — неустойчивым. Чтобы показать это, достаточно перестроить ряд S + ( x , t ) в (0.1) для z + * , у которого Re ( z + * ) > 0 , по формуле
S + ( x , t ) = b ( x , z + * J1 + £ Bn ( x , z k ) exp ( — ( z + V к = 1
—
z k ) ) ) exP ( z + * t ) , B n ( x , z ) =
b ( x , z ) b ( x , z n )
из которой видно, что ряд в скобках сходится, но за счет множителя explz+*t) lim S+ (x, t) = да и такое решение, t ^да содержащее z+*, неустойчиво.
При анализе траекторий полюсов z + и Z + n, к = 0,1,2, . , изображенных на рис. 2, при изменении V от 0 до да следует отметить, что полюса движутся по своим траекториям с разной скоростью: наибольшей скоростью среди них обладает z ( , z + или Z + ■ С увеличением V один из этих полюсов первым пересекает мнимую ось, пусть,
ˆˆ
ˆˆ
например, при V = V crit , после чего при V > V crit
Re ( z + ) > 0 и решение задачи неустойчиво, независимо от того,
пересекли или нет мнимую ось другие полюса. Вывод заключается в том, что область устойчивых решений задачи V e [ o, V crit ] , область неустойчивых решений задачи — V е ( V crit, да ) при фиксированных других параметрах задачи: Y , ц * , a * , . . Полюсы Z ± к = 1,2, . имеют Re ( z ± ( V )) < 0 при V е [ 0, да ) и не образуют неустойчивых решений.
На рис. 3 представлены графики изменения границы между областью устойчивых решений (ОУР) и неустойчивых решений (ОНР) в зависимости от параметров V =у V , ц * , у при K * = 6,5, к * = 5, V * = 1,2, а * = 2,2, р * = 0,4, a * = ^ ц * /р * . При ц * ^ 0 и ц * ^ да решения задачи II неустойчивы при сколь угодно малых V > 0 или V > 0.
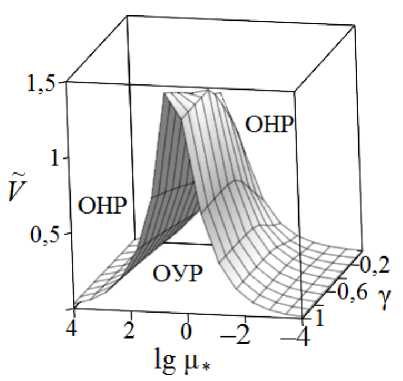
Рис. 3. Граница области устойчивых и неустойчивых решений задачи в пространстве (lg ц * , у , V )
Численный анализ решения задачи. Чтобы проиллюстрировать влияние упругих и теплопроводных свойств подложки на решение задачи, на рис. 4 а , б приведены графики температуры ( а ) и напряжений ( б ) на контакте. Графики получены при значениях параметров задачи, соответствующих покрытию из алюминия толщиной h = 2 мм. Принимались следующие значения параметров материала покрытия: μ = 25,5 ∙ 109 ГПа, ρ = 2,7 ∙ 103 кг/м3, a = 6,24 ∙ 103 м/с, ν = 0,34, K = 0,21 ∙ 103 Вт/(м ∙ К), α = 22,9 ∙ 10–6 1/К, κ = 87,4 ∙ 10–6 м/с2. Скольжение осуществляется со скоростью V = 0,15 м/с при коэффициенте трения f = 0,15. Параметры закона внедрения А( t ) (0.15): А0 = 0,01 h , v 0 =
0,05 мм/с, ε = 10 1/с, t ε = 6,93 ∙ 10–2 с. Безразмерные величины γ , V ˆ принимают следующие значения: γ = 7 ∙ 10-6, V ˆ = 1,052. При этом значения параметров подложки вычисляются через µ * , a * , K * , κ * , значения которых указаны в таблице 1. Значения остальных безразмерных параметров задачи принимаются следующими: ρ * = 0,346, ν * = 1,192, α * = 1,924 (что соответствует покрытию из алюминия на подложке из углеродистой стали).
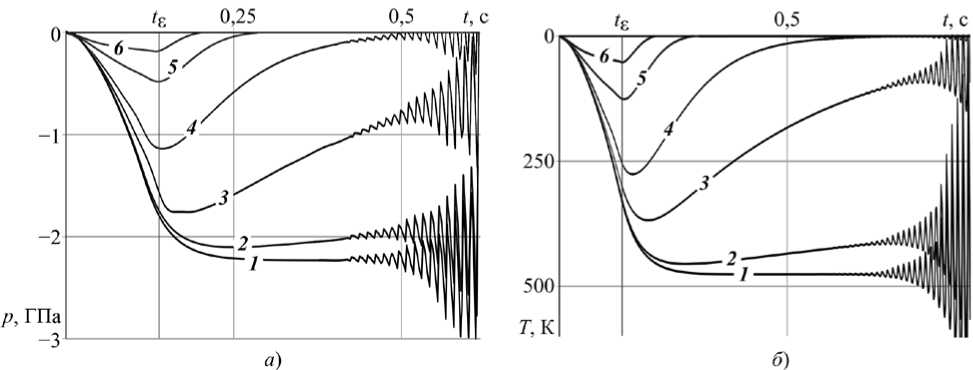
Рис. 4. Графики напряжений p(t) = -σ(h, t) и температуры T(h,t) на скользящем термофрикционном контакте при различных значениях параметров μ , a , K , κ
Таблица 1
Значения безразмерных параметров μ , a , K , κ , использовавшиеся для построения графиков на рис. 4
|
Номер графика |
μ* |
a * |
K * |
κ * |
|
1 |
4,264 ∙ 10-19 |
1,110 ∙ 10-9 |
4,610 ∙ 10-18 |
6,906 ∙ 10-18 |
|
2 |
4,264 ∙ 10-15 |
1,110 ∙ 10-7 |
4,610 ∙ 10-14 |
6,906 ∙ 10-14 |
|
3 |
4,264 ∙ 10-13 |
1,110 ∙ 10-6 |
4,610 ∙ 10-12 |
6,906 ∙ 10-12 |
|
4 |
4,264 ∙ 10-12 |
3,510 ∙ 10-6 |
4,610 ∙ 10-11 |
6,906 ∙ 10-11 |
|
5 |
8,529 ∙ 10-12 |
4,964 ∙ 10-6 |
9,220 ∙ 10-11 |
1,381 ∙ 10-11 |
|
6 |
4,264 ∙ 10-11 |
1,110 ∙ 10-5 |
4,610 ∙ 10-10 |
6,906 ∙ 10-10 |
|
* |
4,264 ∙ 10-1 |
1,110 ∙ 100 |
4,610 ∙ 100 |
6,906 ∙ 100 |
В последней строке таблицы приведены данные для основания из углеродистой стали (для сравнения).
Графики 1 решений динамической задачи, изображенные на рис. 4 а , б , совпадают с соответствующими графиками решений задачи для полосы на жестком основании [14]. С уменьшением жесткости основания (увеличением µ * ) величина напряжений и температуры на контакте стремительно падает, несмотря на ослабление теплопроводных качеств основания (увеличение K * ), что демонстрируют графики 2 – 6 рис. 4. Заметим, что на графиках 2 – 6 рост температуры и напряжений сменяется их убыванием сразу ( 5 , 6 ) или спустя некоторое время ( 2 , 3 , 4 ) после момента t ε окончания активной фазы внедрения жёсткой полуплоскости I в покрытие.
Графики 1 – 4 демонстрируют термоупругодинамически неустойчивое решение задачи, на графиках 5 – 6 изображено устойчивое решение. Заметим, что рост амплитуды напряжений σ( h , t ) несколько опережает рост температуры на контакте T ( h , t ).
Заключение. Исследование решения нестационарной динамической контактной задачи термоупругости о скользящем контакте с учётом трения и разогрева от трения жёсткой полуплоскости с поверхностью упругого покрытия на упругой подложке из другого материала показывает, что основное влияние на напряжения и температуру на контакте в первую очередь оказывают механические характеристики покрытия и подложки, и только во вторую очередь — температурные.Границы области устойчивости также наиболее существенным образом зависят от механических характеристик контакта и в первую очередь от отношения жёсткостей покрытия и подложки — параметра µ * . При приближении µ * к единице ( µ * → 1 ) ширина области устойчивых решений в плоскости µ *, V ˆ принимает наибольшее значение, тогда как при µ * → 0 или µ * → ∞ ширина области уменьшается до сколь угодно малой величины.
Правильный подбор материалов покрытия и подложки на этапе конструирования триботехнических устройств позволяет улучшить их эксплуатационные характеристики, практически исключить возможность возникновения термоупругодинамической неустойчивости и обеспечить безаварийную эксплуатацию триботехнических устройств.
Список литературы Неустойчивость скользящего контакта с покрытием на упругой подложке при наличии трения и разогрева от трения
- Dow, T. A. Thermoelastic instability of sliding contact in the absence of Wear/T. A. Dow, R. A. Burton//Wear. -1972. -Vol. 19, no. 3. -P. 315-328.
- Burton, R. A. Thermoelastic instability in a seal-like configuration/R. A. Burton, V. Nerlikar, S. R. Kilaparti//Wear. -1973. -Vol. 24, no. 2. -P. 177-188.
- Barber, J. R. Stability of Thermoelastic Contact for the Aldo Model/J. R. Barber//J. Appl. Mech. -1981. -Vol. 48, no. 3. -P. 555-558.
- Моров, В. А. Термоупругая неустойчивость фрикционного контакта штампов с полупространством/В. А. Моров, И. Н. Черский//Трение и износ. -1985. -Т. 6, № 1. -С. 27-38.
- Ciavarella, M. Interaction of thermal contact resistance and frictional heating in thermoelastic instability/M. Ciavarella //Int. J. Solids Struct. -2003. -Vol. 40, no. 21. -P. 5583-5597.
- Afferrante, L. Sliding thermoelastodynamic instability/L. Afferrante, M. Ciavarella, J. R. Barber//Proc. R. Soc. A Math. Phys. Eng. Sci. -2006. -Vol. 462, no. 2071. -P. 2161-2176.
- Afferrante, L. A note on thermoelastodynamic instability (TEDI) for a 1D elastic layer: Force control/L. Afferrante, M. Ciavarella//Int. J. Solids Struct. -2007. -Vol. 44, no. 5. -P. 1380-1390.
- Mao, J.-J. Thermoelastic contact instability of a functionally graded layer and a homogeneous half-plane/J.-J. Mao, L.-L. Ke, Y.-S. Wang//Int. J. Solids Struct. -2014. -Vol. 51, no. 23-24. -P. 3962-3972.
- Yi, Y.-B. Effect of convective cooling on frictionally excited thermoelastic instability/Y.-B. Yi, A. Bendawi//Wear. -2012. -Vol. 296, no. 1-2. -P. 583-589.
- Yi, Y.-B. Finite element analysis of thermoelastic instability in intermittent sliding contact/Y.-B. Yi //J. Therm. Stress. -2014. -Vol. 37, no. 7. -P. 870-883.
- Слоновский, Н. В. О термоупругой устойчивости при трении скольжения/Н. В. Слоновский//Прикладная математика и механика. -1969. -Т. 33, № 1. -С. 117-121.
- Пырьев, Ю. А. Анализ устойчивости термоупругого контакта в трибосистеме типа радиальных уплотнений цилиндра/Ю. А. Пырьев, Ю. И. Мандзик//Трение и износ. -1996. -Т. 17, № 5. -С. 621-628.
- Евтушенко, А. А. Влияние изнашивания на развитие термоупругой неустойчивости фрикционного контакта/А. А. Евтушенко, Ю. А. Пырьев//Известия РАН. Механика твердого тела. -1997. -№ 1. -С. 114-121.
- Зеленцов, В. Б. Термоупругодинамическая неустойчивость решения контактной задачи для покрытия с учетом тепловыделения от трения/В. Б. Зеленцов //Вестник ДГТУ. -2014. -Т. 14, № 4. -С. 17-29.
- Zelentsov, V. B. Instability of solution of the dynamic sliding frictional contact problem of coupled thermoelasticity/V. B. Zelentsov //Mater. Phys. Mech. -2015. -Vol. 23. -P. 14-19.
- Зеленцов, В. Б. Неустойчивость скользящего термофрикционного контакта жесткого тела с упругим покрытием, содержащим пьезокерамическую прослойку/В. Б. Зеленцов //Известия высших учебных заведений. Северо-Кавказский регион. Естественные науки. -2015. -№ 4. -С. 52-60.
- Зеленцов, В. Б. Динамическая и квазистатическая неустойчивость скользящего термофрикционного контакта/В. Б. Зеленцов, Б. И. Митрин, С. М. Айзикович//Трение и износ. -2016. -Т. 37, № 3. -С. 280-289.
- Новацкий, В. Вопросы термоупругости/В. Новацкий. -Москва: Изд-во АН СССР, 1962. -363 с.
- Диткин, В. А. Интегральные преобразования и операционные исчисления/В. А. Диткин, А. П. Прудников. -Москва: Физматлит, 1961. -524 с.
- Виленкин, Н. Я. Функциональный анализ/Н. Я. Виленкин ; под ред. С. Г. Крейна. -Москва: Наука, 1964. -425 с.
- Брычков, Ю. А. Интегральные преобразования обобщенных функций/Ю. А. Брычков, А. П. Прудников. -Москва: Наука, 1977. -288 с.
- Тихонов, А. Н. Уравнения математической физики/А. Н. Тихонов, А. А. Самарский. -Москва: Наука, 1977. -735 с.


