Невидимые гиперграни и порождающие многогранники

О порождении множества, многогранных конусов F многогранником P говорят в том случае, когда каждый конус из F является конической оболочкой некоторой гиперграни многогранника P. Понятие порождения исследовано (см., например, [1]) для полных множеств многогранных конусов, то есть множеств, объединение конусов из которых совпадает со всем пространством.

Интерес к понятию порождения обусловлен в большой степени тем, что существуют множества, многогранных конусов, которые вполне могли бы порождаться некоторым многогранником, по которые тем не менее никаким миогограиииком не порождаются. Множество многогранных конусов, которое могло бы порождаться многогранником, называется веером. Определение веера, выглядит следующим образом.

Определение 1. Конечное множество острых полномерных многогранных конусов называется веером, если пересечение любых двух конусов из этого множества, является их общей собственной гранью.

Конус является острым, если начало координат O является его гранью. Поскольку, кроме того, пересечением любых двух конусов веера, так же как и пересечением любых двух гиперграией многог ранника, является их общая собственная грань, то создается впечатление, что всегда, возможно представление веера, показанное на. рис. 1.

Конусы C и K веера, изображенного на рис. 1, являются коническими оболочками заштрихованных гиперграией многогранника P. Другие конусы этого веера, являются коническими оболочками других гиперграией P и вместе с конусами C и K заполняют все двухмерное пространство. Таким образом, рис. 1 представляет случай порождения полного веера, многогранником.

Однако уже в трехмерном пространстве далеко не каждый веер является порождаемым. Например, таким веером является веер G, изображенный на. рис. 2. Построения, приведенные на. рис. 2, заимствованы из [2]. Доказательство непорождае-мости веера G будет приведено в конце статьи.

Мы также покажем, что присутствие конусов C 1 и C 2 в веере G , изображенном на рис. 2, никак не влияет на. существование порождающего многогранника. Это означает, что оставшиеся три конуса веера G не могут входить ни в какой порождаемый веер. Таким образом, анализ структуры, которая не может порождаться многогранником, упрощается и сводится к анализу всего трех конусов.

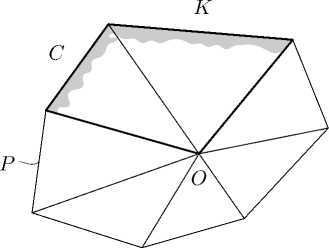
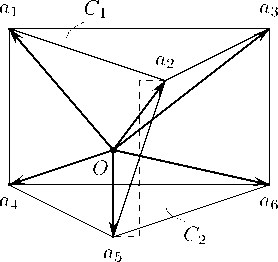
Рис. 2. Непорождаемый веер из пяти конусов в R³

Данная работа, описывает способ, с помощью которого исследование вееров па. порождаемость может проводится па. регулярной основе. Этот способ основан на. последовательном решении трех подзадач.

Во-первых, мы строим пригодное для аналитического исследования формальное определение порождения многогранником неполного веера, например. веера. G без ксшусов C 1 i1 C2. Принятая в настоящий момент в литературе трактовка, порождаемого неполного веера, как части порождаемого полного веера, (см., например, [1]) для регулярного исследования является недостаточной. Решение первой подзадачи опирается на. понятие невидимой гиперграпи многогранника [3].

Вторая подзадача, состоит в построении критерия существования многогранника, порождающего веер, который может быть в том числе и неполным. На настоящий момент все описанные в литературе критерии существования порождающих многогранников (см., например, [4-6]) построены для полных вееров. Решение второй подзадачи основано на. геометрическом методе Александрова. [7].

Наконец, мы иллюстрируем применение построенного критерия. Для этого используется веер G , уже представленный на рис. 2. Рассмотрение веера G интересно тем, что приводит к построению непорождаемого веера в пространстве R³, состоящего всего из трех конусов. В литературе подобный пример описан только для пространства R⁴ (см. [8] п [1]).

Определение порождения для полных вееров основано на. том, что конусы веера, являются коническими оболочками гиперграпей многогранника. Попытка непосредственно перенести это определение на неполные вееры оказывается неприемлемой. Проще всего объясняет ситуацию рис. 3. Здесь смежные конусы C и K , составляющие веер, являются коническими оболочками несмежных заштрихованных граней многогранника P.

Очевидно, что идея определения порождения имеет смысл лишь в том случае, если структура. пересечений конусов порождаемого веера, в точности соответствует структуре пересечений ги-перграпей порождающего многогранника. Поэтому, для того чтобы правильно трактовать ситуации, подобные той, что изображена, на рис. 3, в данной работе при определении порождения используется понятие невидимой гиперграпи многогранника, данное в [3].

Определение 2. Пусть F — гипергрань многогранника. P. Буном говорить, что F невидима из точки v, если одно из двух открытых полупространств, определяемых опорной гиперплоскостью к многограннику P , проходящей через грань F, содержит как точку v, так и многогранник P без грани F.

Геометрический смысл определения 2 очевиден. Предположим, наблюдатель, расположенный в начале координат, смотрит па. непрозрачный многогранник P, изображенный на рис. 3. Что он видит? Очевидно, заштрихованную грань, конической оболочкой которой является конус K, ио не заштрихованную грань, конической оболочкой которой является конус C.

Заметим, что любая гипергрань многогранника, порождающего полный веер, является невидимой из начала, координат (см. рис. 1). Обобщим понятие порождения на возможно неполные вееры следующим образом.

Определение 3. Пусть каждый конус веера. F является конической оболочкой некоторой гиперграпи многогранника P , невидимой из начала координат. В таком случае будем говорить, что веер F порождается зпюгограиинком P. а многогранник P является порож,дающим, для веера. F.

Заметим, что вместо невидимости граней в определении 3 можно потребовать, чтобы начало координат O принадлежало внутренности многогранника P. Преимущество использования невидимых граней состоит в том, что они позволяют выделить два. типа, порождающих многогранников: минимальные и все остальные. Минимальный порождающий многогранник — это многогранник, не содержащий с точки зрения порождения ничего лишнего.

Рассмотрим для примера, рис. 4. Здесь веер,

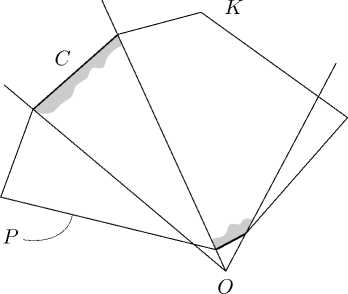
Рис. 3. Конусы C и K являются коническими оболочками граней P, но они не порождаются P

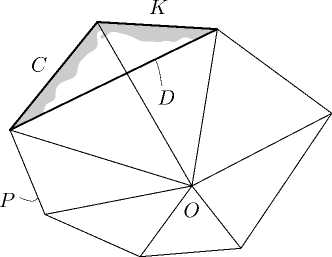
состоящий из конусов C и K , порождается многогранниками PhD. Очевидно, что многогранник Р является избыточным с точки зрения порождения конусов C и K. в то время как многогранник D — пет. Определим минимальный порождающий многогранник следующим образом.

Определение 4. Многогранник, порождающий веер, называется минимальным, если он представим как выпуклая оболочка, конечного числа, вершин, таких, что каждая вершина, лежит па. некотором экстремальном луче одного из конусов веера, и при этом каждый экстремальный луч содержит в точности одну вершину.

Выделение минимальных порождающих многогранников является оправданным благодаря тому, что их вершины находятся во взаимнооднозначном соответствии с экстремальными лучами конусов веера. Это делает рассмотрение порождения неполных вееров более структурным и удобным. Возможность применения минимальных многогранников устанавливается следующей леммой.

Лемма 1. Если веер имеет порождающий многогранник, то он имеет и минимальный порождающий многогранник. □

Доказательство. Пусть Р — порождающий многогранник веера F. Для произвольного конуса C вес>ра F обознач!ш через F c гргшь Р. конической оболочкой которой является C. По определению 3, F c является невидимой из начала координат. В частности, это подразумевает, что начало координат не лежит в аффинной оболочке Fc. Мы можем заключить, что начало координат есть вершина. C. Что означает, что конус C является острым.

Пусть теперь Vc обозначает множество всех вершин Fc. Так как C является острым, все вершины из Vc лежат на. экстре'мальных лучах C. по одной вершине на. каждом из лучей. Обозначим через Pm выпуклую оболочку вершин из объединения множеств Vc для всех конусов C вееpa F. По определению 3. Pm. так яее как Р. является порождающим многогранником для веера F. По построению любая вершина Pm лежит на некотором экстремальном луче F.

Предположим, что экстремальный луч F содержит две различные вершины Pm: v и w . Пусть v обозначает вершину, ближайшую к началу координат. По построению Pm существует конус K веера. F тако!i. что v принадлежит Vk. Поскольку две вершины V k не могут лежать на одном и том же экстремальном луче F, то w не принадлежит Vk.

Теперь рассмотрим произвольную гиперплоскость H, проходящую через v и не проходящую через начало координат О . Легко видеть, что w лежит в одном открытом полупространстве, определяемом H- а О — в другом. Так как w не принадлежит Vk- то это противоречит тому, что грань FK является невидимой из начала координат. Таким образом, никакой экстремальный луч F не содержит более одной вершины Pm. Мы доказали, что Pm является минимальным порождающим многогранником для веера F. ■

Предположим, что задан некоторый базис пространства. Тогда, аффинная оболочка, точек пространства, являющихся концами векторов базиса, есть аффинная гиперплоскость, не проходящая через начало координат. Следовательно, начало координат лежит в одном из открытых полупространств, определяемых данной гиперплоскостью.

Разложим произвольный вектор по векторам базиса. Очевидно, что сумма, коэффициентов разложения равна, единице, если конец вектора, лежит в гиперплоскости; меньше единицы, если конец вектора, лежит в открытом полупространстве, содержащем начало координат; и больше единицы, если конец вектора, лежит в противоположном полупространстве.

Рассматривая сумму коэффициентов разложения минус единица, как высоту над уровнем гиперплоскости, мы можем думать о нижнем полупространстве с точками, лежащими ниже гиперплоскости, и верхнем полупространстве с точками, лежащими выше гиперплоскости.

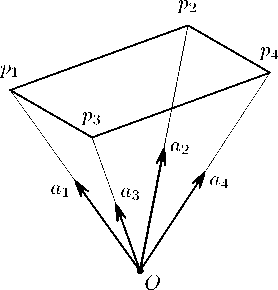
Рис. 5. Точка p4 лежит в аффинной гиперплоскости, задавае-

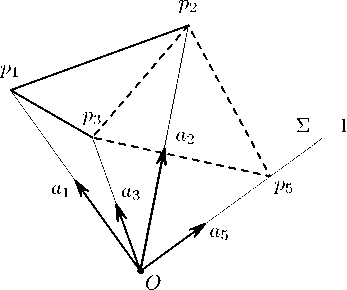
Рис. 6. Точка р₅5 лежит ниже аффинной гиперплоскости, задаваемой точ

ной точками p 1. p2. p з

ками p i. p 2. p з

В частности, если точка, принадлежит порождающему многограннику, а. гиперплоскость является опорной для невидимой из начала, координат гиперграпи этого многогранника, то точка, может лежать только в гиперплоскости, если опа. принадлежит гиперграпи, или ниже гиперплоскости в противном случае (см. рис. 5, 6).

Для того чтобы превратить приведенное геометрическое наблюдение в критерий существования порождающего многогранника, достаточно ввести подходящую систему обозначений и затем использовать технику Александрова. [7], разработанную для многогранников с вершинами па. заданных лучах.

Введем систему обозначений следующим образом. Предположим, что экстремальные лучи всех конусов веера. F задаются векторами a 1 am. Тогда любой конус C вееpa F является конической оболочкой некоторого набора векторов aj-, j Е Е J ( C ). г,те J ( C ) есть подмножество { 1 ,..., т}.

Подмножества S ( C ) множеств J ( C ) определим таким образом, чтобы векторы aj, j Е S ( C ), были линейно независимы и их количество совпадало с размерностью пространства. Векторы aj- j ^Е Е S ( C ). назовем базисом, с вязанным с конусом C. Заметим, что так как мы предполагаем, что все конусы веера, являются полномерными, то такой выбор множеств S ( C ) является заведомо возможным.

{i }us ( с ) Yjaj = 0. Обозначим через D = ( C ) множество векторов y = ( Y 1, • • •, Ym ) таких, что Yi = = 1 для пекоторого i Е J ( C ) \ S ( C ). Yj = 0 для всех j / S ( C ), j = i, a Yj Для j Е S ( C ) опять-таки определяются разложением 52 {i }_us ( с ) Yjaj = 0.

Пусть, наконец. D + ( F ) = Uc_e/D + ( C ) ii D =( F ) = U c _£ f D = ( C ). Тогда верна следующая теорема.

Теорема 1. Веер F является порождаемым тогда и только тогда, когда существует вектор x = = ( x 1 ,..., xm ) такой, что

( hY,xi >  0 V y Е D +( F ).

hY,xi = 0 V y Е D = ( F ).        □ (1)

• [ Xj >  0 ,     j = 1 , ... ,m.

Доказательство. Необходимость. Пусть P — порождающий многогранник веера F. Тогда для некоторых xj >  0, j = 1 ,... ,m, точки pj = = ajjXj являются вершинами P. Пусть x = = ( x 1 ,... ,x_m ). Рассмотрим произвольный вектор Y = ( Y i ,.. .,Ym ) Е D +( C ) U D = ( C ). г,ле C Е F n Yi = 1 для пекоторого i / S ( C ). Мы имеем

• ^x iPi = Y,_{3 eJ ( C} ) -Yj ^x jpj.

Обозначим через F выпуклую оболочку точек Pj, j Е J (C). По пос троению F является гранью многогранника P, невидимой из начала координат. Если y Е D +(C). то ве!ишипа. pi многого>ашшка. P не принадлежит грани F (см. рис. 6). Следовательно, pi лежит ниже гиперплоскости, задаваемой точками pj. j Е S(C). и мы получаем

• ^x i >  X _3E j ( с ) ^{- Y} j ^x j.

Таким образом, мы доказали, что hY,xi >  0.

Аналогично, если y Е D =( C ), то вершина pi миогогу>ап1шка P принадлежит грани F (см. рис. 5). Следовательно, pi принадлежит также гиперплоскости, задаваемой точками pj, j Е S ( C ), откуда, мы находим

• ^x i = X _3£ j ( с ) ^{- Y} j ^x j

и hY, xi = 0. Необходимость доказана.

Достаточность. Пусть вектор x = ( x 1, ..., xm ) удовлетворяет системе (1). Рассмотрим многогранник P, который является выпуклой оболочкой точек pj = aj jxj для всех j = 1 т. и многогранник F , который является выпуклой оболочкой точек pj, j Е J ( C ), для некоторого конуса C ЕF.

Обращая выкладки, которые использовались при доказательстве необходимости, легко видеть, что из условий hY, xi >  0. г,де y Е D +( C ). следует, что точки pi, i Е J ( C ), лежат ниже гиперплоскости, задаваемой точками pj, j Е S ( C ). Аналогично, из условий hY,xi = 0, г де y Е D =( C ), следует, что точки pi, i Е J ( C ) \ S ( C ), лежат в гиперплоскости, задаваемой точками pj, j Е S ( C ).

Таким образом, F является гипергранью P, невидимой из начала координат, а сам P является минимальным порождающим многогранником для веера F. Достаточность доказана. ■

Критерий существования порождающего многогранника. в виде теоремы 1 имеет простое, по важное применение. Для вееров F, состоящих из небольшого числа, конусов, часто удается подобрать такие векторы из множества D +( F ), положительная комбинация которых представима, в виде линейной комбинации векторов из множества. D =( F ). Очевидно, что в этом случае система (1) для веера F неразрешима и, как следствие, многогранник, порождающий веер F , отсутствует.

Продемонстрируем описанную технику на. примере веера G, изображенного на рис. 2. Все векторы, задающие экстремальные лучи этого веера, построены по вершинам правильной треугольной призмы, за исключением векторов a2 и a5, которые немного сдвинуты в направлениях ±(a3 — a 1). С учетом такого сдвига для некоторых а, в, 5 > 0, 5=1 справедливы уравнения a i — a з — a 4 + a 6 = 0, a 3 — 5a 6 — aa 2 + ea 5 = 0,          (2)

a 4 — 5a 1 — aa 5 + ea 2 = 0 .

Пусть K 1 обозначает конус, экстремальные лучи которого заданы векторами a 1 , a ₂ , a 4 , a 5; K ₂

обозначает конус, экстремальные лучи которого заданы векторами a 2 ,a 3 , a 5 , a 6: ii K 3 обозначает конус, экстремальные лучи которого заданы векторами a 1 , a 3 , a 4 , a 6. Пусть S ( K 1) = { 1 , 2 , 5 }. S ( K 2) = { 2 , 5 , 6 } 11 S ( K 3) = { 3 , 4 , 6 } . Тогда, уравнения (2) определяют векторы

( - 1 , - 0 , — 1 , — 1 , — 0 , — 1) G D =( K з) C D =( G ) ,

^{( — 0} , ^{— a} , - ¹ , - ⁰ , ^—Д -5 ) E D =⁽ К 2) ^C D =⁽ G ) , (3) ( -5, -в, — 0 , — 1 , —a, — 0) G D =( K i) C D =( G ) .

Просуммировав векторы (3) и поделив результат на 1 — 5, мы получим вектор

(1        ^, 0 , 0 a, 1) G D +( K 2) C D +( G ) .

1 —5      1 —5

В соответствии с теоремой 1 это означает, что веер G является непорождаемым.

Так как критерий теоремы 1 верен в том числе и для неполных вееров, то мы доказали па. самом деле больше, чем просто пепорождаемость веера. G. Веер G, естественно возникающий из треугольной призмы, является полным и состоит из пяти конусов K 1. K 2- K 3. C 1 11 C 2- г,де C 1 i1 C 2 обозначают конусы, экстремальные лучи которых заданы векторами a 1, a 2, a 3 и a4, a 5, a 6 соответственно.

Ничто ne мешает рассмотреть наряду с полным веером G неполный веер G' , состоящий всего из трех конусов K 1, K 2 и K 3. Поскольку множества D = ( K 1), D =( K 2) и D =( K 3) содержатся как во множество D =( G ). так и во зтожество D =( G0 ). а множество D +( K 2) содержится как во множестве D + ( G )- так и во множество D + ( G0 ). то доказательство пепорождаемости, проведенное для веера. G. доказывает также и пепорождаемость G0.

Интересно, что трехмерный веер G0 является минимальным непорождаемым веером, так как любой двухмерный веер и любой веер, состоящий из двух конусов, являются порождаемыми. Пример непорождаемого веера, состоящего всего из трех конусов, в литературе описан только для пространства. R4 (см. [8] ii [1]).