Неволновая математическая модель водного солитона

Изучение солитонов началось с известного наблюдения Рассела за появлением и движением водного солитона. С тех пор появилось много различных математических моделей солитона, а водный солитон превратился в незначительный частный случай большой группы физических явлений, соответствующих этим математическим моделям [2-5]. Однако, насколько известно автору, эти модели рассматривают волновые процессы, а в водных солитонах явным образом наблюдаются процессы переноса вещества. Морская волна переносит энергию, но оставляет на месте воду – вода только колеблется по вертикали. Солитон переносит воду – цунами, продолжающее движение по суше, должно быть доказательством этого. Кроме того, перенос воды по горизонтали 162

невозможно объяснить колебанием масс по вертикали и преобразованием кинетической энергии в потенциальную и обратно. Перенос воды по горизонтали должен быть связан с горизонтальным потоком кинетической энергии, который не может быть получен из потенциальной энергии. Можно вспомнить про ветер, но даже в первом наблюдении Рассела не было ветра. Посмотрим на фотографии цунами – см. рис. 1 и рис. 2. Кажется неубедительным представление о том, что причиной движения этой махины является ветер и нелинейность среды. Создается впечатление, что внутри этого "устройства" есть собственный двигатель, а сопротивление среды – лишь катализатор, сила, которая давит на педаль газа.

Поэтому ниже рассматривается неволновая математическая модель, рассматриваются потоки вещества и энергии внутри водного солитона, выявляется источник энергии.

Рассмотрим вначале солитон с цилиндрическим основанием. Его математическая модель аналогична математической модели песчаного вихря. Тело солитона пронизывают потоки гравитационной энергии, которые создается массовыми токами. Формульные зависимости между токами и потоками энергии рассмотрены в [1] для песчаного вихря. Этими же зависимостями можно воспользоваться в данном случае.

Рис. 1.

Рис. 2.

2.    Вертикальная устойчивость

Явное отличие, которое необходимо обосновать, -колоколообразная форма водяного солитона в отличие от цилиндрической формы песчаного вихря. Это отличие обусловлено тем, что верхние слои солитона давят на нижние слои силой тяжести. Рассмотрим, к чему это приводит.

В частности, в теле солитона существует поток энергии, направленный по вертикали, с плотностью

S z

2 ^α

-W 2, .

давления, действующую в каждом сечении на тело радиусом R ,

1 ^R             1 ^R ₃ j h πα R ⁴

Fn =-   5 2nr • dr = jh.яа\ r3 • dr = —^-^.

zo             z                  ϕ ϕ c0               c 0

солитона

Поскольку поток энергии (30) направлен вниз, то противоположно направленная ему сила (32) направлена вверх и поддерживает солитон в вертикальном положении. Ей противодействует и

уравновешивает ее сила тяжести.

Отсюда следует, что радиус солитона должен убывать при увеличении z . Оценим зависимость радиуса от z , обозначив ее как R ( z ) . Итак,

F zo

j h πα

ϕϕ

4 c

(R (z)1.

Сила тяжести части вихря расположенного выше уровня равна L

P ( z ) = - J p • n^R ( z ) ) dz .                               (34)

z где р – плотность воды. Силы (33, 34) уравновешиваются, т.е.

• j^'^ (R ⁽ z ^{) ) 4} = J p • ⁿ ( R ⁽ z ) ) dz .                   (35)

• 4    c

z

Дифференцируя это выражение, получаем:

jha d (R (z)) )=- pn(R ( z))

• 4    cdz

или

(R ( z)) d (R ( z )) = -n,(36)

dz где pc

П = —---.(36а)

^j ϕ ^h ϕ^α

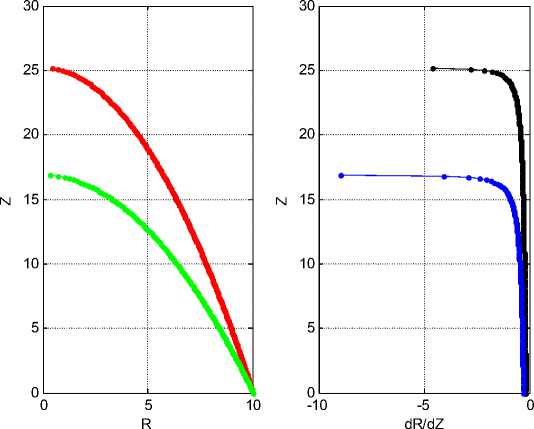
Рис. 3.

Функция R ( z ) определяется как решение этого уравнения. Для этого должны быть задано начальное условие R (0) . Для иллюстрации на рис. 3 показаны функции R ( z ) и R '( z ) при R (0) = 10 и п = 2 - верхние кривые,. п = 3 - нижние кривые.

При данном R ( z ) можно по (34) найти вес солитона

Po =-p • пJ (R(z))2 dz,(37)

o объем солитона

L

Vo = пJ(R(z)J^ dz(38)

o и высоту центра тяжести солитона

L

Lo = p.f J (R(z))2 z • dz .(39)

oo

Потенциальная энергия солитона

Wp = PL g(40)

где g - ускорение свободного падения. Объединяя (39, 40), находим L

Wp = p-^ J (r (z ))2 z •dz.(41)

go

Кинетическая энергия солитона W_k , в котором масса циркулирует "верх-вниз", равна потенциальной энергии (если пренебречь потерями на внутреннее трение), т.е.

W k » W p . (42)

Эта энергия является энергией массовых токов. Потери этой энергии на внутреннее трение пополняются энергией гравитационного поля.

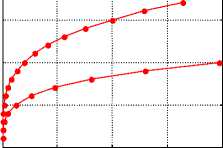
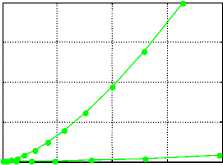
В момент образования солитона он получает энергию W o ~ W k ~ W p • Из (36, 41) следует, что энергия W o , начальный радиус R o = R (0) зависит от начальной энергии W o (при данных p , g , n )• В свою очередь, от R (0) зависят высота, форма, объем, вес солитона. Рассмотрим эти зависимости при p = 1, g = 10 , n = 2 - см. рис. 4, где верхние кривые относятся к значениям W_o , указанным на оси, а нижние к значениям W o /10 •

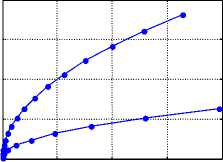
На рис. 5 показана зависимость высоты солитона от нижнего радиуса L_o = f ( R o ) . Вид этой функции зависит от коэффициента найти n . При известной из наблюдений функции L o = f ( R o ) можно найти значение коэффициента найти η . На рис. 5

коэффициент η = 2, 4, 7 (верхняя, средняя, нижняя кривые соответственно).

Wo x 104

x 106

Wo x 104

Wo x 104

x 106

Wo

x 104

Рис. 4.

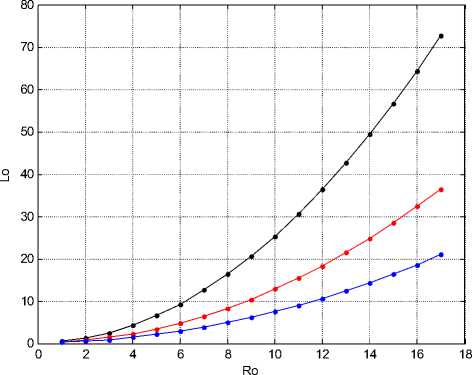
Рис. 5.

5 . Движение солитона

Траектория движения солитона плохо предсказуема. Для того чтобы показать, что движение солитона совершается за счет внутренней энергии (а не за счет силы ветра) нужно обратиться к рассмотрению внутреннего потока электромагнитной энергии, как это сделано в [6] для песчаного вихря. Там показано, что, кроме вертикального потока энергии существует еще поток энергии, направленный против скорости движения солитона. В соответствии с законом сохранения импульса, этот поток создает механический импульс солитона, направленный вдоль скорости . Таким образом, существует положительная обратная связь между скоростью солитона и его механическим импульсом: начав движение, солитон разгоняется .

Гравитационная энергия в солитоне преобразуется в кинетическую энергию внутренних струй воды, которая, в свою очередь, преобразуется в тепловую энергию трения и в кинетическую энергию движения солитона.