New method for assessing the degree of deterioration of a building into account a decrease in the heat-shielding properties of its enclosing structures

Цитирование: Шаумаров, С.С. О новой методике оценки степени износа зданий с учетом снижения теплозащитных свойств его ограждающих конструкций / С. С. Шаумаров, Е. В. Щипачева // Журн. Сиб. федер. ун-та. Техника и технологии, 2021, 14(5). С. 590–599. DOI: 10.17516/1999-494X-0336

the thermal regime of the building [11–13], as noted by the researchers themselves [14], when used in real design, it will not allow, in most cases, to implement energy efficient measures due to a number of restrictions associated with a specific construction situation, or factors that were not taken into account in the modeling. Some of these factors were the following:

• –    changes in the temperature of the air and internal surfaces in the room do not coincide in time and differ in magnitude;

• –    climatic characteristics change according to certain laws;

• –    physical processes of interaction of external fences with the surrounding air occur in a medium moving at an arbitrary speed.

In addition, certain difficulties are associated with taking into account in the proposed model [11, 12] building air conditioning systems.

Development of a mathematical model of the thermal regime of the building

In connection with the above, when constructing a mathematical model of the thermal regime of a building, we took into account these factors, and the effect of heat supply, heating and ventilation systems is not explicitly present.

In Making a through research mathematical modeling of interaction between external protections to climatic factors it was based on a number of assumptions.

One such assumption is that the room consists of three partitions, a floor, a ceiling and an outer wall with a window. It was assumed that the temperature in such a room would depend on the temperatures on the inner surfaces of the partitions, the outer wall and the window. At the same time, the structure of the inner partitions and the outer wall is taken into account. This makes it possible to calculate the temperature in rooms, both old panel buildings and modern ones, during the construction of which new technologies were used or a defect was allowed.

As one of the major physical parameters that influence the room climate in the model considering stream of solar radiation into the room through the window and its heating indoor air due to solar heat, and the temperature change of the partitions and the outer wall s due to radiation heat transfer. In addition, it was necessary to take into account the specifics of the participation of the radiant and convective components in the process of general heat exchange, which manifests itself in a different sequence of heat transfer to the air and the inner surfaces of the room. Indeed, convective heat enters the air and is transferred from it to the room. At the same time, the change in the temperature of the air and surfaces in the room does not coincide in time and differ in magnitude. Radiant heat goes directly to surfaces and changes their temperature. Air does not participate in radiant heat transfer. In this case, the air temperature follows the surface temperature fluctuations with some delay. At the same time, the developed model does not explicitly take into account the type of the building's heat supply system, the presence of a forced-type ventilation system, etc., that is, artificial sources of influence on the microclimate of the room.

The formation of the microclimate of the premises of the building, taking into account the accepted assumptions, occurs as a result of the processes of air exchange (mass exchange – variations in the infiltration of the outside air) and heat exchange. For consideration of these processes must take into account the requirements for the characteristics of the micro climate of premises and the factors affecting them, under the laws of interaction of barriers to the internal and external environments, heat and mass transfer processes in the heating and cooling surfaces. The phenomena occurring in structures and materials during the transfer of heat, moisture and air through them are also of great importance in the formation of the microclimate of a room. And, finally, it was necessary to take into account the external factor – the characteristics of the outdoor climate and the laws of their change.

The comfort of indoor conditions in buildings is defined as a function of variations in the above processes. In this case, the most comfortable conditions are met by the parameters of processes, the limit of variations of which tends to zero in time, that is, in the idealized case, remain constant for a long period. In real conditions, a change in the speed of movement of internal air, a decrease in the temperature of the internal surfaces of fences, a decrease in the air temperature inside the room leads to a violation of conditions that meet the requirement of comfort.

Thus, the task is reduced to finding a number of physical parameters of the internal environment that determine the formation of the microclimate in the room and the conditions for their slight change over time, taking into account the current regional climate change.

Consider a physical and mathematical model of heat and mass transfer.

The formation of a microclimate in a room, as a result of the interaction of the enclosing structures with external factors (climate characteristics), e g o dynamics obeys the laws of heat and mass transfer. Under the influence of the difference between outside and inside temperatures, solar radiation and wind, the room loses heat through fences in winter and heats up in summer. Gravitational forces, wind and ventilation create pressure drops, leading to air flow between communicating rooms (mass transfer) and to its filtration through the pores of the material and leaks in fences. Precipitation, moisture release in rooms, the difference in humidity between indoor and outdoor air lead to moisture exchange through fences, under the influence of which it is possible to moisten materials and deteriorate the protective properties and durability of external walls and coatings. Processes of forming the heat with the room, you need to burst out laughing – studied in detail in close connection with each other, for their mutual influence can be quite substantial. For example, air filtration and humidification of structures can increase the heat loss of a room in winter by several times. At the same time, the creation of a favorable air environment in a room requires the organization of its air exchange and moisture exchange with the outside environment.

In the process of heat exchange, the air of the main (not jet streams) volume of the room, the inner surfaces of the fences, the volumes of air jets and the external environment are involved. The following types of heat exchange occur between the listed elements:

• –    convective heat exchange occurs between the air and the surfaces of the enclosures;

• –    radiant heat exchange – between individual surfaces.

As a result of turbulent mixing of non-isothermal jets of air with the air of the main volume of the room, «jet» heat exchange occurs. The inner surfaces of external fences, mainly by heat conduction through the thickness of the structures and heat exchange, transfer heat to the outside air. An important component of the process that forms the thermal regime of a room is heat exchange on surfaces. The heat balance of any surface in the room (in stationary and non-stationary conditions) is represented on the basis of the law of conservation of energy by the equation [14]

Li + Ki + Ti = 0, where Li – radiant, Ki – convective and Ti – conductive (thermal conductivity) components of heat transfer on the i- th surface. In the presence of additional sources or sinks of heat, the corresponding components are added to the balance equation.

Radiant heat exchange in a room occurs under conditions of a limited range of temperature values, certain radiation properties of surfaces, the geometry of their location, and other factors.

To construct a mathematical model of heat and mass transfer processes, a system of equations of dynamics was considered in the form of a plane problem [15]:

ЭР d²U — = и--

Эх      dxdz

ЭР      d2V

— = и-- ду      дудг.

with the boundary condition: U| G = 0; V| Г = 0 and the continuity equation applied to plane jets [16]:

др = 9(р ■ U) д(р-У) d(p-W) дт дх ду dz

wherein R –pressure differential across the inner and outer surfaces of the enclosure; U, V, W – projections of the velocity of the medium on the x, y, z axes; ρ is the air density; τ is the time; M is the mass air flow rate per unit of time per unit of volume occupied by the crack; η – dynamic viscosity of air.

To solve the resulting system, consisting of (1) and (2), we used the Runge – Kutta and Galerkin methods [17].

For a mathematical model of the heat transfer process from the viewpoint of the effect of external factors on the climatic room climate, it was derived dependence of the temperature field barriers, as a function of I «free volume» – the integral value of the volume of space through which the outdoor air into the room. In this case, the characteristics of an elementary cell (area of space) «free volume» are designated by symbols δx , δy , δz . Then we used the differential equations of heat conduction and heat transfer. At the same time, it was necessary to take into account that these physical processes are carried out in air moving with a speed v . Therefore, the heat conduction equations were considered not in their classical form [18], but taking into account the moving medium. To derive this equation, we used the first law of thermodynamics and considered the case when the temperature T of the medium is determined by the relation

cpdtT =

where c p is the heat capacity at constant pressure; P is the pressure; T is the temperature; ρ is the density; ɛ is the density of internal energy.

Next, the temperature evolution equation was used, which was found from the internal energy balance equation [19]

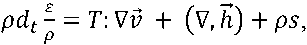
describing the rate of change of the internal energy of the body under the action of contact forces (T: ∇ , v .).

Taking a number of assumptions and approximations (no heat source inside the building), the final expression for the heat conduction equation of the moving medium was obtained, to which the heat transfer equation was added [20] and the system was considered:

at дт

+ vgradt = k^t

- = k^T, дт

where t is the air temperature of the free volume cell; τ is the time; k – coefficient of thermal diffusivity of air; – air flow speed, m/s.

The solution of system (5) based on the Fourier method gives the expression for the temperature T:

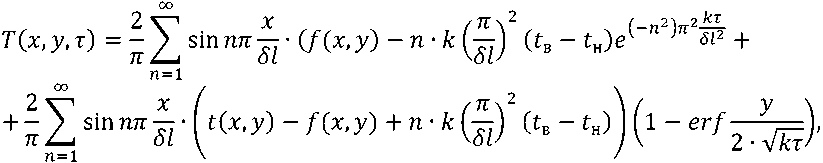
where T is the required temperature of the enclosure, t n is the temperature of the outside air; t в – internal air temperature; δ l the diameter of an elementary spatial cell of free volume; erf (·) is the integral of probabilities; f (x, y) – temperature distribution in the fence at the initial moment of time.

As follows from the presented mathematical model of the interaction of the enclosing structures with external factors, the model explicitly lacks terms that take into account convective and radiant heat exchanges, as well as the influence of various jets. However, these characteristics are taken into account indirectly by the function f ( x, y, τ ) as an integral result of the formation of the temperature field.

To identify the physical parameters of the enclosing structures responsible for the formation of comfortable conditions of the internal environment, based on the numerical solution of the initial system of equations of dynamics (1) and continuity (2) with respect to the initially sought value of the mass air flow rate per unit of time per unit of free volume, one can go to the volumetric air flow W [m ³ / s] entering the room per unit of time. This transition was carried out using the coefficient of dynamic viscosity of air η on the basis of the obtained semi-empirical dependence using the method of dimensions [19, 20]:

c * I] * 5x ■ Sy " D , where |∆P| – module of the pressure gradient on the inner and outer surfaces of the fence; с – empirical coefficient; D is the coefficient depending on the size of the regular grid, at the nodes i, j of which the solution of the system consisting of (1) and (2) is obtained:

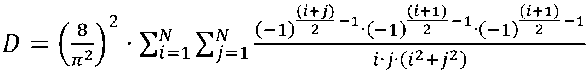
Taking the free volume of the unit cell for δ x = δ y = δ z = δ l, (7) presented whether in the form of

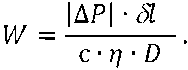
Determination of the dependence of the physical state of the premises on external climatic factors

Thus, the parameter W [m ³ / s] – the change in air flow through the cell of free volume, determines the dependence of the physical state of the room on external climatic factors. The values of this parameter are a function of the unit cell size of the free volume (the degree of porosity of the material, crevices, etc.) and the pressure drop on the inner and outer sides of the enclosing structure. Expression (6) describes the change in the temperature field of the fence in time depending on the value of δ l for a given physical state of external factors. The dependence of these two parameters is obvious: the larger the value of W, the lower the temperature gradient between indoor and outdoor air, all other factors being equal.

In Fig. (a) the surface of the air flow rate through the cell of free volume per unit time is presented as a function of the cell diameter and the modulus of the pressure gradient, calculated on the basis of Shepard's interpolation method [17–20]. The same figure under the letters (b) and (c) shows the dependence of this parameter on the pressure gradient at fixed values of the cell diameter and its dependence on the cell diameter at fixed values of the pressure gradient, respectively.

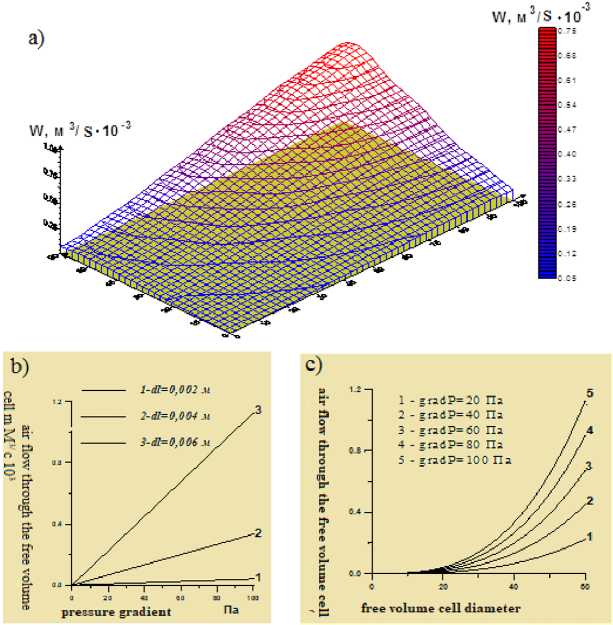
a) is the surface of the air flow rate through the cell of free volume per unit of time, as a function of the cell diameter and the modulus of the pressure gradient; b) – dependence of the air flow rate through the cell of free volume on the pressure gradient at a fixed value of the cell diameter; c) – dependence of the air flow rate through the cell of free volume on the diameter of the cell at a fixed value of the pressure gradient

Fig. Dependencies of air flow through the free volume cell

The analysis of the obtained dependencies showed the following. With a cell diameter within 1mm ≤ d ≤ 2mm ( for d ≤ 1 mm , the cells belong to natural pores) and a pressure gradient between the inner and outer sides of the enclosing structure is less than 34 Pa, the air flow through such a cell is similar to its passage through the pores of the enclosure. Thus, these parameters, all other factors being equal, determine the physical state of the environment in the room, providing normal comfortable conditions. When the specified values are exceeded, the air consumption increases sharply (exponentially – Fig., c), which in winter leads to a cooling of the room, and in summer – to its heating.

Conclusion

The practical application of the W parameter makes it possible to diagnose the quality of the material used for fencing by tabulating (based on the coefficients of thermal conductivity and thermal diffusivity) the time of complete transformation of temperature fields and further comparing this time with the time of transformation of the temperature fields of real enclosing structures by measurements. In other words, the stated theoretical approach is a scientific basis for the development of a methodology for diagnosing the quality of the material of the enclosing structure and can be used to assess the degree of deterioration of a building.

As a result of the research carried out, a mathematical model of the interaction of the building envelope with external climatic factors was developed, taking into account the regularities of changes in the characteristics of the outdoor climate, the specifics of the participation of the convective component in the process of general heat exchange and the features of the process of thermal conductivity in a moving medium, as a result of which it most fully reflects the specifics of the formation of the thermal regime buildings in areas of dry hot climate.

As a criterion that determines the physical state of the external enclosing structure during its interaction with the external environment, the theoretically established parameter W [m 3 / s] is proposed – the change in air flow through the cell of free volume, the value of which is a function of the size of the unit cell (degree of porosity of the material, defectiveness its structure) and the pressure gradient on the inner and outer sides of the fence, which makes it possible to assess the degree of wear in general using one parameter.