New Region Growing based on Thresholding Technique Applied to MRI Data

Published Online June 2015 in MECS

Medical imaging includes conventional projection radiography, computed topography (CT), magnetic resonance imaging (MRI), and ultrasound. MRI has several advantages over other imaging techniques enabling it to provide 3D data with high contrasts between soft tissues. However, the amount of data is far too much for manual analysis/interpretation, and this has been one of the biggest obstacles in the effective use of MRI. The segmentation of medical images is an important first step for most image related application and visualization tasks. It provides assistance for medical doctors to find out the diseases inside the body without the surgery procedure, to reduce the image reading time, to find the location of a lesion, and to determine an estimate of the probability of a disease.

There are many types of image segmentation techniques [1]. Among them, histogram-based [2-4], graph cuts [5-6], genetic algorithms [15], and region- based [7-14] techniques which are the most popular. The histogram techniques [2-4] had been tried to solve threshold problem in histogram- and region-based methods. The histogram-based segmentation technique produces a binary image based on the threshold value. The intensities of object and background pixels tend to cluster into two sets in the histogram with threshold between these two sets [4]. However, it is really difficult to find a general threshold for all cases to determine the threshold value for segmentation. For that, graph cut image segmentation techniques [5,6] used two kinds of seed pixels as “object” and “background”, providing hard constraints for segmentation. For the background seeds, it is needed to put seeds pixel in each tissue described as background, and each pixel in the image is described to belong to object or belong to background.

The region-based segmentation technique in [7-14] segments an image which has strong boundaries into several small regions, followed by merge procedure using specific threshold. In both histogram-based and regionbased segmentation techniques, if the threshold is not correct, the contour of object will be destroyed. Wu et al. [7] described a top down region-based image segmentation technique for medical images that contains three major regions: background and two tissues. This method can only segment 2D images and cannot segment 3D images or images which contain more than two tissues. The work carried by Yu et al. [8] segments the image using only region-boundary model to extract the organ from MRI image. They merged region and boundary model for cerebral cortical segmentation in MRI.

The region growing technique can work efficiently in medical imaging segmentation if one can guarantee optimal initial seeds [9], as well as the threshold criterion used to stop growing outside a region. In seeded region growing, seed selection is crucial but can be seen as an external task, often done by hand in medical image processing. Unseeded RG was also proposed. Hsieh et al. [10] used an algorithm integrating fuzzy c-means and RG techniques for automated tumor image segmentation from patients with menigioma. Only non-contrasted T1 and T2-weighted MRI are included in the analysis. The study’s aims were to correctly locate tumors in the images, and to detect those situated in the midline position of the brain. Mendoza et al. [11] proposed a selfassessed adaptive RG technique to segment bone CT image. They relied on a self-tuning approach to deal with a great variety of imaging conditions requiring limited user intervention (one seed). The detection of the optimal parameters was managed internally using a measure of the varying contrast of the growing region, and the stopping criterion was adapted to the noise level in the dataset thanks to the sampling strategy used for the assessment function. Moreover, they obtained similarity around 86% of segmentation results with the ground truth tissues. Kavitha et al. [12] proposed an effective modified RG technique for detection of brain tumor. Modified RG included an orientation constraint in addition to the normal intensity constrain. The performance of this technique was systematically evaluated using the MRI brain images received from the public sources. For appropriate thresholds, Ayman et al. [13] presented region growing (RG) technique for medical image segmentation and obtained good results for low noise level. But this method failed to extract the true tissue in the case of high noise levels and achieves similar results as Del-Fresno et al. [14], more discussions can be shown in [13]. Zanaty and Ghiduk [15] combined GA and region growing to produce accurate medical image segmentation, and to overcome the oversegmentation problem. Although the previous algorithms had suppressed the impact of noise and intensity inhomogeneity to some extent, these algorithms still produce misclassified small regions. In MRIs, the weak boundaries have very similar pixels values around the boundaries, so it is difficult to segment the tissues of WM and GM. Furthermore, region growing method cannot specifically segment the tissues because the growing of the region will not stop on the boundaries and will add outside pixels of the tissue to the organ. To solve this problem, this paper presents a probabilistic threshold for automatic region growing method. The automatic region growing technique is proposed to segment tissues with weak boundaries. It includes a threshold that can be varied over the image as a function of intensity probability to provide the better segmentation results. The efficiency of the proposed algorithm is demonstrated by extensive segmentation experiments using real MRIs, compared with other state of the art algorithms.

In this paper, the proposed algorithm hybridizes the seed selection, local search, and thresholding algorithms with the region growing technique for accurate segmentation of MRIs. The thresholding process works by iterative homogeneity criterion in the region growing algorithm. The proposed method was found to achieve better results than those using the most recent stand-alone GA approaches.

The rest of the paper is organized as follows. Related work is discussed in section II. In section III, the proposed approach is described. The results obtained with simulated brain MR data are presented in section IV. Our conclusion is presented in section V.

• II.    Related Work

The basic idea of image segmentation can be described as follows. Given a set of data x = { x , x₂ ,.., x_N } and uniformity predicates P, we desire to obtain a partition of the data into disjoint nonempty groups X = { v , v ₂,.., v_k } subject to the following conditions:

• ⁽¹⁾    U k = 1 V i = X

• (2)    v i П v j = Ф , i ^ ^j

• (3)    P ( v i ) = TRUE , i = 1,2,.., k

• ⁽⁴⁾    P ( v, и v ) = FALSE , i ^ ^j

The first condition ensures that every data value must be assigned to a group, while the second condition ensures that a data value can be assigned to only one group. The third and fourth conditions imply that every data value in one group must satisfy the uniformity predicate while data values from two different groups must fail the uniformity criterion. To obtain a 3D MR image, the positional information about the tissues must be recorded. This involves isolating the source of each component of the MR signal to a particular voxel using the technique of spatial encoding. MR image segmentation involves the separation of image pixels into regions comprising different tissue type. All MR images are affected by random noise. The noise comes from the stray current in the detector coil due to the fluctuating magnetic fields arising from random ionic currents in the body, or the thermal fluctuations in the detector coil itself [15-16]. When the level of noise is significant in an MR image, tissues that are similar in contrast could not be delineated effectively, causing error in tissue segmentation. In MRIs, intensity non-uniformity can affect computational analysis of the image due to the variance in signal intensity. It is manifested as smooth spatially varying signal intensity across the image and caused by several factors including inhomogeneous radio frequency (RF) fields (caused by distortion of the RF field by the object being scanned or non-uniformity of the transmission field). The boundaries among tissues become weak when RF and noise increase. Furthermore, inside each tissue the pixels of the region have very similar intensities and outside each tissue the pixels have different intensities from inside the region. Also, the pixels on the boundaries will have intensities between the intensities inside and outside. The boundaries become strong if there is big difference between the pixels inside and outside the tissues, and become weak if the difference is small [16]. In both cases, the pixels intensities on the boundaries have different values from inside and outside pixels intensities. Furthermore, the numbers of pixels which have the same intensity inside or outside the tissue(s) are much bigger than the number of pixels on the boundaries. So, probabilities of these pixels intensities in the tissue or in the other tissues have higher value than pixels intensities on the boundaries.

• III.    The Proposed Approach

In general, an image can be described by a twodimensional function f(x, y), where (x, y) denotes the spatial coordinates, and the intensity value at (x, y) is f (x, y) E [0,255]. The region growing technique uses only a few seed pixels as “object”, and describes each pixel in the object to belong to the edges of this object. The simple region growing (RG) technique merges neighboring pixels P to pixels P inside the region, xy according to | i(p ) - i(p )|< t , where T is a fixed threshold and I(•) is the pixel intensity value. The proposed RG algorithm can be described by iteratively merging similar pixels into sets or merging sub-regions into larger regions in 3 main steps:

a- Choice of the seed pixels;

b- Local search according to a similarity rule;

c- Thresholding algorithm for growing the seed regions by including adjacent pixels that satisfy the similarity rule.

The first two steps are repeated until there are no more adjacent pixels to be included in a seed region. The challenge that faces RG technique is to select a good seed and threshold capable to segment images containing weak boundaries. However, it is really difficult to find a general threshold for all cases. In addition, there is no universal algorithm for segmentation of every medical image, since each imaging system has its own specific limitations.

• A.    Procedure For Choosing The Seed Pixels

A proposed seed region growing algorithm is developed for these reasons to work automatically. The simplest region growing method consists in merging neighboring pixels p of the pixel inside the region p , according to |i ( p ) _ I ( p )| <  t , where T is a fixed threshold and I ( • ) is the gray level. This method has two problems: (1) it can lead to a chaining effect especially for images with low contrast shape boundaries or images with alighting shift, and (2) the choice of T . We solved the first problem by using the homogeneity test 1 1 ( P x ) - RA <  T , where RA is the seed pixel. The seed pixel is candidate from grey-level histogram. It assumes that the level is composed of regions with different gray level ranges; the histogram of the level can be separated into a number of peaks (modes), each corresponding to one region. The initial seed is chosen through histogram of each segment level by position of maximum amplitude.

• B.    Local Search

The partitioned histogram generates the initial seeds corresponding to the different segments in the image. The next step is to search for the best seed to avoid oversegmentation when region growing is applied. Local search is performed on the initial seed pixel by applying a mask on each initial seed. A seed is grown by merging neighboring pixels (on mask). Typically, the homogeneity criterion is defined as summation of the difference between the intensity of the initial seed and the neighbour intensities in the mask. If the homogeneity criterion § is satisfied, the initial seed will be a candidate seed. Else, another point in the mask should be selected.

• C.    Thresholding Algorithm

The thresholding algorithm can be described as follows: The Average of minimum and maximum gray levels (h max ,h min) of the image is obtained. The image is divided into two parts using initial threshold T old . The average gray level values for each part (mean 1 , mean 2) is computed. We update threshold value by T new =(mean 1 + mean ₂ )/2 and stop when the condition | t_w - T_a J< delta is satisfied.

Thresholding Algorithm

Let I(x,y) image, seed (x,y), hmax = maximum gray value in image, hmin = minimum gray value in image.

Told = ( hmax + hmin)/2

delta=0.1*(h max + h min )

Find mean₁ for cover region

Find mean₂ for non-cover region

T_new = (mean₁+mean₂)/2

Stop if |Tnew – Told| < delta

• D.    Automatic Seed Region Growing

The basis of the RG method is to segment an image of N pixels into regions with respect to a set of seeds [18] using only the initial seed pixels. The seed positions and the threshold T new are fed to seed region algorithm from local search and thresholding procedures. The seeds are grown by merging neighboring pixels whose properties are most similar to the premerged region. Typically, the homogeneity criterion is defined as the difference between the intensity of the candidate pixel and the average intensity of the premerged region. If the homogeneity criterion (threshold T new ) is satisfied, the candidate pixel will be merged to the premerged region. The procedure is iterative: at each step, a pixel is merged according to the homogeneity criterion (under threshold T _new ). This process is repeated until no more pixels are assigned to the region [19]. Since we only perform the seed growing on edge pixels, the amount of data needed to be processed is much reduced, resulting in increased speed.

• IV.    Experimental Results

The experiments were performed on images taken from the classical simulated brain database of McGill University (Brain Web [20]). Each original image has a slice thickness of 1mm, no intensity inhomogeneities, corrupted by 6% salt and pepper noise, with image size of 129 X 129 pixels, as shown in Fig.2. The comparison core

S for each algorithm as proposed in [36] is defined as follows:

A ^ A ref

A U A ref

where A represents the set of pixels belonging to a class as found by a particular method and A represents the reference cluster pixels.

• A.    Experiment With MR Image

In this section, we experiment the proposed technique on slice#72 at noise level 6% and spatial RF level 20% as shown in Fig.1. The seeds are selected from the histogram; Fig.2, as the maximum represented value in the image of Fig.1. The local search is applied to pick the best seed in the accumulator. To prove the efficiency of proposed algorithm, we evaluated the accuracy (score S ) of each output segment corresponding to threshold T new . After applying the proposed algorithm, six seeds and the corresponding segments are obtained. As shown in Table I, the spatial positions of the resulting seeds are P(49,33) for segment#1, P(99,68) for segment#2, P(55,62) for segment#3, P(95,35) for segment#4, P(56,103) for segment#5 and P(110,62) for segment#6. Table I describes the relation between the thresholds and the accuracy S for each resultant segment. Figs.(3-8) show the performance of thresholds in relation to the accuracy S for slice#72, as well as the optimal threshold for each segment. For example, the optimal threshold for segment#1 is 34.13, and the accuracy of this segment is 0.95 as shown in Fig.(3).

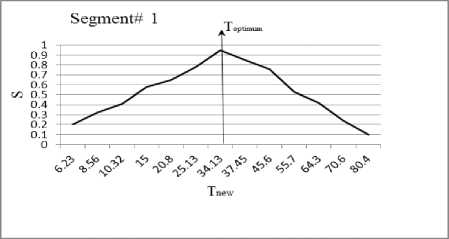
Fig. 3. The effect of threshold Tnew on the accuracy S for segment#1.

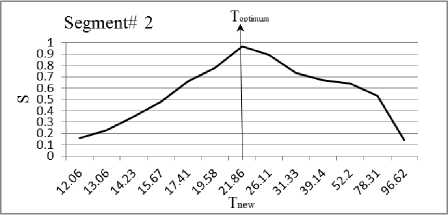
Fig. 4. The effect of threshold Tnew on the accuracy S for segment#2.

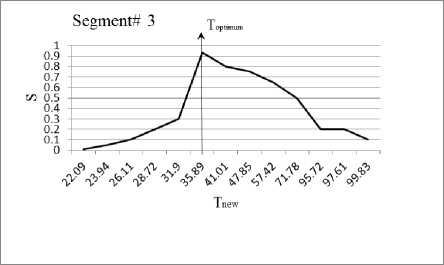
Fig. 5. The effect of threshold Tnew on the accuracy S for segment#3

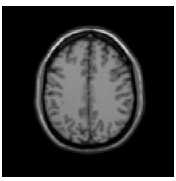
Fig. 1. Slice#72 with noise level 6% and spatial RF level 20%

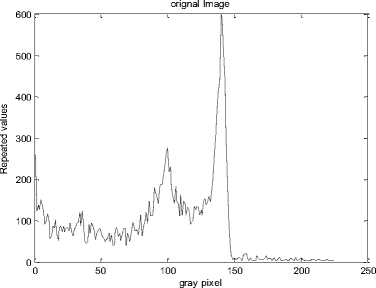
Fig. 2. Histogram of slice#72

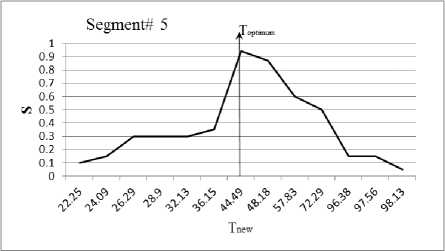
Fig. 7. The effect of threshold Tnew on the accuracy S for segment#5

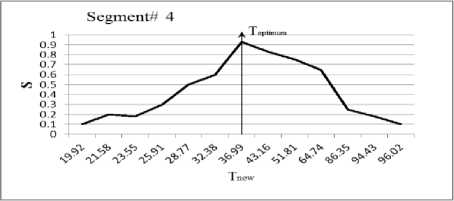
Fig. 6. The effect of threshold Tnew on the accuracy S for segment#4

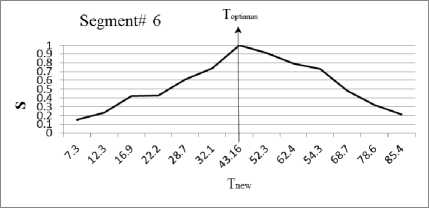
Fig. 8. The effect of threshold Tnew on the accuracy S for segment#6.

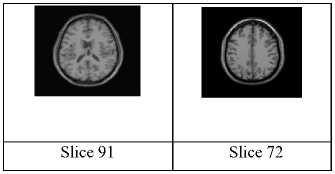
Fig.9. Test images: (a) Original slices from the 3D simulated data (slice 91 and slice 72)[20].

(e) P(88,81), T =30

(a) P(36,86),

T=25,

S =0.87

(b) P(12,63), T =   25,

S=0.13

(c) P(25,18), T = 20, S =1

(d) P(48,99),

T=25,

S =0.85

S = 0.80

(f) P(65,67), T = 25 S=0.40

(i) P(36,86), T optimum 20.5824

S =0.95

(j) P(108,64)	(k) P(25,18),	(l) P(48,99),	(m) P(88,81),	(n) P(65,67),
T optimum       =	T optimum =	T optimal =	T optimum =	T optimum =
34.43	8.3	64.6272	17.92	23.04
S =0.97	S = 1	S =0.86	S = 0.97	S = 0.98

Fig. 10. The output of the proposed method (from i to n) versus the Zanaty and Ghiduk [15] (from a to f) for slice 91.

LuiujLJLea
(a) P(49,35, T = 20 S=0.10	(b) P(99,6), T=25 S=0.40	(c) P(55,6), T=30 S =0.35	(d) (95,73), T=30 S =0.45	(e) P(56,103), T=30 S =0.30	(f) P(110,62), T=25 S=1
I о И фИрИ» ДоИ
(i) P(49,35, T optimum =32 S =0.95	(j) P(99,68), T optimum = 22.297 S =0.97	(k) P(55,62), T optimum = 33.38 S =0.93	(l) P(95,73), T optimum = 32.58 S =0.90	(m)   P(56,103), T optimum = 43.8 S =0.94	(n) P(110,62), T optimum = 43.16 S = 1

Fig. 11. The output of the proposed method (from i to n) versus Zanaty and Ghiduk [15] (from a to f) for slice 72.

Table 1. Relation between the thresholds T new and the segmentation accuracy of slice 72.

Segment# 1 P(49,33)		Segment# 2 P(99,68)		Segment# 3 P(55,62)		Segment# 4 P(95,73)		Segment# 5 P(56,103)			Segment# 6 P(110,62)
T New	S	T New	S	T New	S	T New	S	T New	S	T New	S
6.23	0.2	12.06	0.16	22.09	0.01	19.92	0.1	22.25	0.1	7.3	0.15
8.56	0.32	13.06	0.23	23.94	0.05	21.58	0.2	24.09	0.15	12.3	0.23
10.32	0.41	14.23	0.35	26.11	0.1	23.55	0.18	26.29	0.3	16.9	0.42
15	0.58	15.67	0.48	28.72	0.2	25.91	0.3	28.9	0.3	22.2	0.43
20.8	0.65	17.41	0.66	31.9	0.3	28.77	0.5	32.13	0.3	28.7	0.61
25.13	0.78	19.58	0.78	35.89	0.93	32.38	0.6	36.15	0.35	32.1	0.74
34.13	0.95	21.86	0.97	41.01	0.8	36.99	0.93	44.49	0.94	43.16	1
37.45	0.85	26.11	0.89	47.85	0.75	43.16	0.83	48.18	0.87	52.3	0.91
45.6	0.76	31.33	0.73	57.42	0.65	51.81	0.75	57.83	0.6	62.4	0.79
55.7	0.53	39.14	0.67	71.78	0.5	64.74	0.65	72.29	0.5	54.3	0.73
64.3	0.42	52.2	0.64	95.72	0.2	86.35	0.25	96.38	0.15	68.7	0.48
70.6	0.95	78.31	0.53	97.61	0.2	94.43	0.18	97.56	0.15	78.6	0.32
80.4	0.10	96.62	0.14	99.83	0.1	96.02	0.1	98.13	0.05	85.4	0.21

Table 2. Comparison between the results of the proposed method and GA in [15].

Image		Seg. #1	Seg. #2	Seg. #3	Seg. #4	Seg. #5	Seg. #6	Average
Slice 91	S old	0.87	0.13	1	0.85	0.8	0.40	0.675
	S ne	0.95	0.97	1	0.86	0.97	0.98	0.955
Slice 72	S old	0.10	0.40	0.35	0.45	0.30	1	0.4333
	S ne	0.95	0.97	0.93	0.90	0.94	1	0.943

• B.    Comparative Results

In this section, the proposed method is compared to that of Zanaty and Ghiduk [15] to prove its efficiency. Their method combined GA and region growing to select the seed positions automatically. In this experiment, two original slices from brain MR McGill database; slices 91 and 72; are used with slice thickness of 1mm, 6% noise and RF 20% as shown in Fig. (9). There are several parameters in GAs that have to be tuned by the user, among which are the population size, probabilities of performing crossover and mutation, maximum of generations, chromosome length, and the termination criteria. In these experiments, we set the population size to be 20; probabilities of performing crossover and mutation to be 0.6, 0.05; maximum of generations to be 50; chromosome length to be 20 and the termination criteria to be 0.001. Also, for local search procedure, we set δ to be 10.

Table 2 shows the accuracy for each slice when applying the proposed algorithm (with threshold T optimum and accuracy S new ) and GA algorithm of Zanaty and Ghiduk [10] (with threshold T and accuracy S_old ) to the above test data. As shown in Table II, we found that the mean segmentation accuracy of the proposed method increased by 28% and 41%, over Zanaty and Ghiduk [15] method for slices 91 and 72 , respectively. For example, Fig.(10 (a, b, c, d and f)) shows the result of the GA segmentation at seed positions: P(36,86), P(112,63), P(25,18), P(48,99) and P(65,67) respectively and at T=25, but for segment in Fig.(10e) at T=30 and P(88,81). These test images showed that segmentation results are good compared to GA algorithm, the average improvement reaches 41%. Overall, the proposed method is more stable and achieves much better performance than the others in all different classes even with misleading of true tissue.

• V.    Conclusion

This paper presents an approach that could improve the accuracy of medical images segmentation. The proposed method combines the process of choosing the seeds, local search procedure, and thresholded region growing to improve the accuracy of image segmentation and the time needed for the search process. Without any details or information about the target medical image, the proposed approach randomly selects an initial set throughout the image. The output of the initial seeds, are fed to local search procedure to find the best seed around initial seed.

The proposed algorithm has been implemented on PC i3, 3 GHZ. It has been tested on four MRI images with noise level 6%. The superiority of the proposed algorithm is demonstrated by comparing its performance with the recent GA algorithms carried by Zanaty and Ghadik [15]. We noted that the segmentation accuracy of the proposed method is improved by 28% (for first image) and 41% (for second image). Finally, the application of the proposed algorithm to other abnormal brain cases will be the topic for further research.