Низкочастотная (105) сдвиговая упругость обычных и полимерных жидкостей

Важнейшей структурной характеристикой жидкости является период релаксации τ — время перехода из неравновесного в равновесное состояние. В теории жидкости Френкеля [1] период релаксации оценивается по скорости самодиффу-зии приравниванием этого периода к времени оседлого существования отдельных молекул, и для маловязких жидкостей он равен 10-11-10-12 с. Оценка времени релаксации неравновесного состояния по реологической модели Максвелла также дает значение для τ порядка 10-10с. Следовательно, для таких жидкостей динамическая сдвиговая упругость может быть обнаружена именно при таких периодах сдвиговых колебаний и эта область недостижима для акустических методов исследования.

Однако в работах [2-4] впервые было показано, что все жидкости, независимо от их вязкости и полярности, обладают сдвиговой упругостью при частоте сдвиговых колебаний порядка 105 Гц.

Детальное исследование данного свойства для различных жидкостей в зависимости от толщины прослойки показало, что сдвиговая упругость является свойством жидкости в объеме. Наличие низкочастотной сдвиговой упругости говорит о том, что в жидкостях существует неизвестная ранее низкочастотная вязкоупругая релаксация, определяемая, по-видимому, коллективными взаимодействиями больших групп молекул — кластеров. Время релаксации больших групп молекул может намного порядков превышать время оседлого существования отдельных молекул.

Акустический резонансный метод

Акустический резонансный метод измерения сдвиговой упругости жидкостей основан на применении пьезокварцевого кристалла X-18.5 : среза, в виде прямоугольного бруска [5, 6]. Грань, колеблющаяся на основной резонансной частоте в собственной плоскости, соприкасается на одном конце с прослойкой исследуемой жидкости, накрытой кварцевой накладкой. При тангенциальных смещениях грани пьезокварца прослойка жидкости будет испытывать деформации сдвига и в ней должны установиться стоячие сдвиговые волны. Накладка при этом будет практически покоиться. В зависимости от толщины прослойки жидкости изменяются параметры резонансной кривой пьезокварца: собственная резонансная частота и ширина резонансной кривой. Если прослойка жидкости обладает сдвиговой упругостью, то резонансная частота будет возрастать по сравнению с частотой свободного пьезокварца. В случае, если бы в прослойке действовали только диссипативные вязкие силы, то резонансная частота должна уменьшаться. Метод отличается высокой чувствительностью, и применим в широком диапазоне измеряемых вязкостей.

Была решена общая задача взаимодействия колебательной системы пьезокварц — прослойка жидкости — накладка [5, 6].

Решение данной задачи дает следующее выражение для комплексного сдвига резонансной частоты пьезокварца:

∗∗

_{Δ f} ∗₌ S ⋅ χ ^∗ G ^∗ 4 π ² Mf 0

⋅

1 + cos(2 ⋅χ∗H -ϕ∗) sin(2 ⋅ χ∗ H -ϕ∗) ,

где S — площадь основания накладки, χ∗ = β - iα — комплексное волновое число жидкости, β — его действительная, α — мнимая части, Н — толщина жидкой прослойки, G* — комплексный модуль сдвига, ϕ*- комплексный сдвиг фазы при отражении волны от границы жидкость-накладка, М — масса пьезокварца, f0 — резонансная частота.

Разделение (1) на действительную Δ f ^' и мнимую Δ f ^"  части дает для сдвигов частот следующие выражения:

∆ f ^' =

S 4 π ² Mf 0

∆ f ^" =

S 4 π ² Mf 0

( G ^' β + G ^" α ) sin 2 β H + ( G ^' α - G ^" β ) sh 2 α H ch 2 α H - cos 2 β H

( G ^" β - G ^' α ) sin 2 β H + ( G ^" α - G ^' β ) sh 2 α H ch 2 α H - cos 2 β H

При малых толщинах жидкой прослойки, когда толщина много меньше длины сдвиговой волны, Н << λ и, в предположении, что накладка при колебаниях пьезокварца практически покоится ( ϕ^∗ =0), формулы (2) и (3) предельно упрощаются, и для действительной и мнимой частей комплексного модуля сдвига получаются следующие расчетные формулы:

'   4 π ² Mf 0 ∆ f ^' H "

G=           , G =

S

4 π ² Mf 0 ∆ f ^" H S

Для тангенса угла механических потерь будем иметь:

tg θ = ^{G "} _' G

∆ f ^"

. ∆ f ^'

Мнимый сдвиг резонансной частоты ∆ f́ˈ определяется изменением затухания колебательной системы, т.е. он равен половине изменения ширины резонансной кривой.

Другой способ определения G^' основан на измерении длины сдвиговых волн

λ по экспериментально найденным максимумам затухания. Приравнивая к нулю производную по толщине от мнимого сдвига частоты (3), получим положения λ экстремальных значений в виде H = n , где четные значения n относятся к максимальным, а нечетные значения — к минимальным значениям. Отсюда можно видеть, что в случае с накладкой первый максимум затухания будет наблюдаться при толщине прослойки, равной λ/2. Используя соотношение

( χ ^∗ ) ² = ^{ω 2} ∗ ^ρ

для G^' получим следующую расчетную формулу:

G ^' = λ ² f ² ρ cos θ ⋅ cos ²  ,

где f 0 — резонансная частота пьезокварца, ρ — плотность исследуемой жидкости, θ — угол механических потерь.

Экспериментальные результаты

Порядок проведения измерений был следующий. Сразу же после очистки на рабочую поверхность пьезокварца наносилась исследуемая жидкость. После определения толщины прослойки измерялись резонансная частота и ширина резонансной кривой при различных толщинах прослойки жидкости. Из выражения (4) можно видеть, что при наличии у жидкостей комплексного модуля сдвига зависимости действительного и мнимого сдвига резонансной частоты должны быть пропорциональны обратной величине толщины прослойки жидкости. Именно такие зависимости получаются со всеми исследованными жидкостями. На рис. 1 показаны зависимости действительного сдвига частоты пьезокварца от обратной толщины пленки для трех жидкостей: триэтиленгликоля, дибутилфталата и воды. Видно, что линейные зависимости сходятся к началу координат, что свидетельствует о наличии у этих жидкостей объемного модуля сдвига. На рис. 2 приводятся зависимости мнимого сдвига частоты от обратной толщины прослойки для тех же жидкостей. Зависимости также линейные, сходящиеся к началу координат [5, 6, 7].

Из рис. 1 и 2 можно определить значения действительного и мнимого сдвигов резонансной частоты и по выражениям (4) и (5) рассчитать значения действительного модуля сдвига G' и тангенса угла механических потерь tgθ. Так например для дибутилфталата G' = 0.82·105 Па, а tgθ = 0.21 [7]. Полученные ре- зультаты для других жидкостей приведены в табл. 1. В первом столбце указаны температуры эксперимента, во втором столбце приведены измеренные значения модуля сдвиговой упругости, в третьем — значения тангенса угла механических потерь. В следующем столбце даны значения табличной вязкости, а в последнем столбце приведены значения вязкости, рассчитанные по формуле реологической модели Максвелла 7^ =

С (1 + tg² У ) to tg #

Наличие сдвиговой упругости при низких частотах показывает, что в жидкостях существует неизвестный ранее низкочастотный вязкоупругий релаксационный процесс. Тот факт, что у большинства жидкостей тангенс угла механических потерь оказывается меньше единицы, говорит о том, что частота наблюдаемого вязкоупругого релаксационного процесса меньше частоты эксперимента, которая составляла 74 кГц.

Из табл. 1 видно, что для жидкостей рассчитанные вязкости оказываются намного больше известных табличных значений. Так, например, для дибутилфталата п т = 0.02 Пат, П м = 0.9 Пат. Простая механическая модель Максвелла с одним временем релаксации не может адекватно описывать поведения реальных жидкостей. Тем не менее, можно предположить, что при малых сдвиговых колебаниях структура жидкости остается неизменной, и это может соответствовать большим вязкостям, т.е. аномально большим периодам релаксации. Табличная же вязкость будет относиться к жидкости с разрушенной пространственной структурой, соответствующей ламинарному течению в обычных визкозиметрах, где сдвиговые деформации равны бесконечности.

Доказательство возможности распространения низкочастотных сдвиговых волн в жидкостях явилось бы важным подтверждением того, что наблюдаемая сдвиговая упругость является свойством жидкости в объеме. При дальнейшем увеличении толщины жидкой прослойки H будет наблюдаться осцилляция сдвигов частот. Когда толщина слоя жидкости будет равна половине длины сдвиговой волны, должен наблюдаться первый максимум затухания пьезокварца. Таким образом, можно реализовать ультразвуковой интерферометр на сдвиговых волнах в жидкости [5-8].

На рис. 3 показаны экспериментальные результаты для ПМС-52000 [5, 6]. Кривая 1 относится к зависимости действительного сдвига частоты от толщины прослойки, а кривая 2 — к мнимому сдвигу частоты. Из графика следует, что для этой жидкости X = 220 мкм. По расстоянию А Н между первым минимумом и максимумом действительного сдвига частоты для тангенса угла механических потерь получим значение, равное 0,5. По формуле (6) сдвиговая упругость для ПМС-52000 оказывается равной 2.4-10 5 Па. Это значение немного меньше значения, приведенного в табл. 1, полученного первым способом, когда H <<  X [5, 6].

На рис. 3 сплошными линиями нанесены теоретические кривые, построенные по формулам (2) и (3) для полученных значений упругости и угла механических потерь. Совпадение экспериментальных и теоритических кривых удовлетворительное. Результаты исследования других жидкостей приведены в табл. 2.

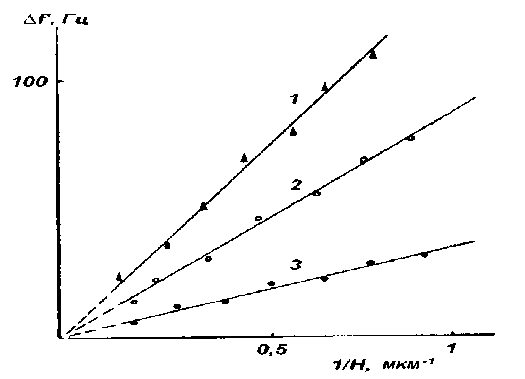
Рис. 1. Зависимости A f от 1/ Н для триэтиленгликоля (1), дибутилфталата (2) и воды (3).

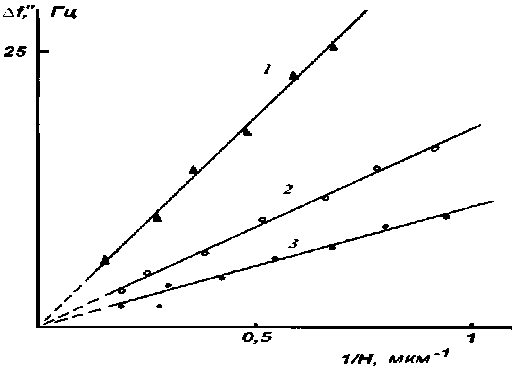
Рис. 2. Зависимости A f " от 1/ Н для триэтиленгликоля (1), дибутилфталата (2) и воды (3)

Таблица 1

Вязкоупругие характеристики различных жидкостей

№	Жидкости	t ° C	G - 10 -5 , Па	tg 0	П т , Па - с	П м , Па - с
1.	Вода	23	0,31	0,3	0,001	0,242
2.	Дибутилфталат	21	0,82	0,21	0,02	0,9
3.	Диметилфталат	23	0,97	0,11	0,016	1,91
4.	Этиленгликоль	23	0,91	0,24	0,019	0,861
5.	Триэтиленгликоль	24	1,28	0,27	0,032	1,101
6.	Диэтиленгликоль	23	1,46	0,31	0,034	1,07
7.	Вазелиновое масло	24	1,36	0,51	0,099	0,71

ВЕСТНИК БУРЯТСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА

8.	ПМС-100	23	0,6	0,5	0,1	0,322
9.	ПМС-400	21	1,24	0,75	0,4	0,555
10.	ПМС-900	22	1,35	0,8	0,9	0,595
11.	ПЭС-1	23	9,83	0,11	0,003	19,448
12.	ПЭС-2	24	4,81	0,63	0,012	2,32
13.	ПЭС-3	24	3,45	0,87	0,014	1,516
14.	ПМС-52000	24	2,6	0,5	52	1,391

АГ, Гц

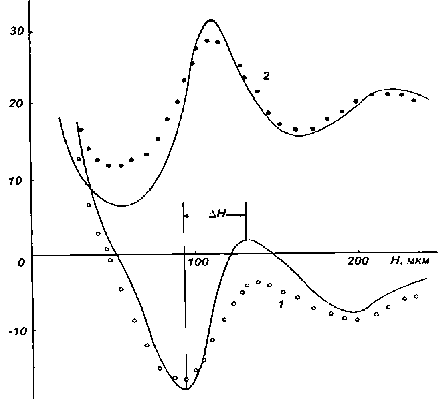
Рис. 3. Зависимости теоретических (сплошные линии) и экспериментальных (точки)

сдвигов частот от толщины жидкой прослойки для ПМС-52000: 1 — действительный, 2 — мнимый сдвиг частот

Таблица 2

Модули упругости жидкостей, рассчитанные по длине сдвиговых волн

Жидкости	t ° C	Р - 10 -3 , кг/м3	X , мкм	G - 10 -5 , Па	G - 10 -5 , Па При Н << X
ПМС-400	22	0.97	160	1.00	1.24
ПМС-900	23	0.98	170	1.08	1.35
ПМС-5384	23	0.98	200	1.80	2.12
ПМС-20000	24	0.98	210	1.93	2.36
ПМС-52000	23	0.98	220	2.40	2.60

Таким образом, измерение сдвиговой упругости жидкостей двумя способами акустического резонансного метода и их удовлетворительное согласие показывает, что низкочастотная сдвиговая упругость является объемным свойством жидкостей. Это доказывает, что в жидкостях существует низкочастотная вязкоупругая релаксация.

Для объяснения низкочастотного релаксационного процесса в жидкостях профессором Сандитовым Д.С. предложена кластерная модель строения жидко- сти [9-11]. Обсуждается модель Исаковича-Чабан [12], где сильновязкая жидкость рассматривается как микронеоднородная среда, состоящая из двух динамических компонентов: упорядоченных микрообластей — кластеров, расположенных в неупорядоченной рыхлоупакованной матрице. При внешних воздействиях кластеры испытывают перестройку, что выражается в диффузионном обмене “дырками” — возбужденными молекулами между этими двумя компонентами. Время жизни кластеров должно быть больше периода звуковых колебаний. По отношению к ним не делается других ограничений.

Профессор Сандитов Д.С. предполагает, что подобная динамическая структурная микронеоднородность характерна не только для сильновязких жидкостей, но и для простых жидкостей с малой вязкостью, т.е. является характерной чертой структуры всех жидкостей. Между сильновязкими и слабовязкими жидкостями нет принципиального качественного различия. Есть лишь количественное различие, а именно время жизни кластеров у простых жидкостей существенно меньше, чем у сильновязких жидкостей [7-11].

С этих позиций низкочастотная вязкоупругая релаксация жидкостей обусловлена распадом и восстановлением таких флуктуационных кластеров — динамических микронеоднородностей структуры, которые с течением времени образуются и распадаются. Предполагается, что распад кластера происходит путем перехода “связанная молекула — свободная молекула”, напоминающего распад капли жидкости за счет испарения отдельных молекул. Такой многоступенчатый процесс характеризуется большим временем релаксации т. Таким образом, время жизни кластера велико не из-за кинетических единиц крупных размеров, а вследствие большого числа связанных молекул z, входящих в кластер. В свою очередь, из-за достаточно большого времени жизни кластер не успевает реагировать на внешние низкочастотные воздействия, а это и означает, что жидкость при низких частотах (порядка 105 Гц) проявляет упругие свойства. Предварительная оценка, проведенная в рамках кластерной модели, приводит к сравнительно высокому значению среднего числа кинетических единиц, входящих в кластер, равному z ~ 102-104 [7-11].

Энтропийная трактовка предэкспоненциального множителя В в известном уравнении времени релаксации приводит к выводу о том, что величина Вл для низкочастотного релаксационного процесса в z раз больше, чем в случае высоко- частотного релаксационного перехода.

По приближенной формуле

U =

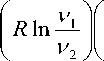
T 1

—

- 1

т

T ₂

где T 1 и T 2 — температуры максимумов на спектре внутреннего трения (tg # -T) соответственно при частотах V 1 = 40 кГц и V 2 = 74 кГц, для вазелинового масла получена следующая оценка энергии активации: U «21,6 кДж/моль (~5 ккал/моль). По-видимому, вязкоупругая релаксация в жидкостях относится к низкоэнергетическим физическим процессам [7-11]. Исследования низкочастотного неньютоновского поведения жидкости рассматриваются также в работах других исследователей [13-18].