Низкочастотная вязкоупругая релаксация в полимерных жидкостях

Сдвиговая упругость жидкостей при высоких частотах воздействия, порядка 1010 Гц, известна давно и объясняется характером диффузионной подвижности отдельных частиц [1, 2]. Частота перехода из жидкого в упруго-твердое состояние, в этом случае, сравнима с частотой колебаний молекулы. При таких высоких частотах молекулы жидкости не успевают реагировать на внешнее воздействие, и жидкость ведет себя как твердое упругое тело.

Однако в работах [3, 4], было установлено наличие сдвиговой упругости у различных жидкостей при частотах порядка 105 Гц. Это свидетельствует о том, что в жидкостях наряду с высокочастотным существует низкочастотная вязко- упругая релаксация и природа этого необычного явления — низкочастотной сдвиговой упругости жидкостей — остается во многом неясной [5-12].

Метод

В настоящей работе проведено исследование низкочастотной вязкоупругой релаксации в полимерных жидкостях и ее сравнение с ^-процессом релаксации в аморфных полимерах. В качестве объектов исследований использованы полиор-ганосилоксановые жидкости, широко применяющиеся в современной технике. Характерные свойства этих полимерных жидкостей — низкие температуры стеклования, повышенная термостойкость, хорошие диэлектрические, а также гидрофобные свойства, значительная сжимаемость, малая величина коэффициента поверхностного натяжения; вязкость их слабо зависит от температуры. Эти жидкости обладают специфическими механическими и реологическими свойствами, которые связаны со слабым межмолекулярным взаимодействием и с высокой гибкостью полимерной силоксановой цепи [13].

Для исследования вязкоупругих свойств полиорганосилоксановых жидкостей использован акустический резонансный метод, основанный на изучении влияния сил добавочной связи на резонансные характеристики колебательной системы. Резонатор, пьезокварцевый кристалл Х-18.5° среза, совершает тангенциальные смещения на основной резонансной частоте. Исследуемая жидкость помещается между поверхностями пьезокварца и покоящейся твердой накладки и испытывает чисто сдвиговые деформации, при этом в жидкости устанавливаются стоячие сдвиговые волны. Поскольку действие добавочной связи меняет как резонансную частоту пьезокварца, так и его затухание, то волновое число пьезокварца оказывается величиной комплексной. Решение задачи взаимодействия резонатора с прослойкой жидкости и твердой накладкой дает для ком- плексного сдвига резонансной частоты Af * = Af ‘ + iAf‘‘ следующее выражение [4, 11]:

_ SG * к * 1 + cos(2 k * H -ф *)                   ₍₁₎

f = 4п2Mfo '  sin(2к * H -ф*)  , где G* = G‘ + iG" — комплексный модуль сдвига жидкости, S — площадь основания накладки, H — толщина жидкой прослойки, M — масса резонатора, f — его резонансная частота, к * — комплексное волновое число; ф * — комплексный сдвиг фазы при отражении сдвиговой волны от границы жидкость — накладка.

Согласно теории метода, считая накладку практически покоящейся вследствие слабого воздействия на нее со стороны жидкости ( ф = 0) и толщину прослойки жидкости много меньшей длины сдвиговой волны, комплексный модуль сдвига и тангенс угла механических потерь будут определяться выражениями:

4п2 Mf0 Af * H           f =AT

S        ’           g G 'A f' ’

Из выражения (2) комплексный сдвиг резонансной частоты пьезокварца A f* должен быть пропорционален обратной величине толщины прослойки. В работе использован пьезокварц массой 6.24 г и основной резонансной частотой 73.2 кГц, площадь основания накладки 0.2 см². В эксперименте измеряются толщина прослойки жидкости H и сдвиги резонансной частоты. Мнимый сдвиг частоты A f "

ВЕСТНИК БУРЯТСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА.

равен половине изменения ширины резонансной кривой. По формулам (2) вычисляются основные вязкоупругие параметры жидкостей.

Экспериментальные результаты и обсуждение

Исследование вязкоупругих свойств гомологического ряда полиэтилсилоксановых жидкостей показало, что зависимость сдвига резонансной частоты от обратной величины толщины жидкой прослойки для всех исследованных ПЭС-жидкостей линейна, что свидетельствует о наличии у них объемного модуля сдвига. Линейные зависимости получены и для мнимого сдвига резонансной частоты. В табл. 1 приведены результаты исследования вязкоупругих параметров полиэтилсилоксановых жидкостей. В первом столбце указана температура эксперимента, во втором столбце приведены измеренные значения модуля сдвиговой упругости, в третьем — тангенс угла механических потерь. В следующем столбце даны значения табличной вязкости. В последнем столбце приведены значения эффективной вязкости. Полагая, что механизм наблюдаемой вязкоупругой релаксации описывается реологической моделью Максвелла, эффективная вязкость рассчитана по следующей формуле:

= G '(1 + tg 29) 2nfotg9

.

Можно видеть, что для маловязких жидкостей рассчитанные вязкости оказываются намного больше известных табличных значений. Необходимо учитывать, что простая механическая модель Максвелла с одним временем релаксации приближенно описывает поведение реальных жидкостей. Тем не менее, можно предположить, что при малых сдвиговых колебаниях структура маловязких ПЭС-жидкостей остается неизменной и это может соответствовать большим вязкостям, т.е. аномально большим временам релаксации.

Тангенс угла механических потерь tgθ для ПЭС-жидкостей возрастает. По модели Максвелла частота релаксационного процесса может быть определена выражением fрел = f0⋅tgθ , (4) тогда частота релаксации наблюдаемого процесса приближается к частоте сдвиговых колебаний, используемой в эксперименте, проходит через нее и в дальнейшем уходит в область более высоких частот.

Таблица 1

Экспериментальные результаты исследования вязкоупругих параметров полиэтилсилоксановых жидкостей

Жидкости	T, oC	G ′ ⋅ 10-5 Па	tg θ	η т , Па·с	η м , Па·с	Число атомов Si в цепи
ПЭС-1	23	9.83	0.11	0.003	19,45	2
ПЭС-2	24	4.81	0.63	0.012	2,32	3
ПЭС-3	24	3.45	0.87	0.014	1,52	4
ПЭС-4	23	2.96	2.00	0.046	1,61	5
ПЭС-5	24	5.90	6.60	0,388	8,67	15

Для проведения исследования температурной зависимости комплексного модуля сдвига акустическим резонансным методом система пьезокварц — про- слойка жидкости — накладка помещалась в термостатируемую ячейку [14]. На рис. 1 представлена экспериментальная зависимость тангенса угла механических потерь от температуры для жидкости ПЭС-2.

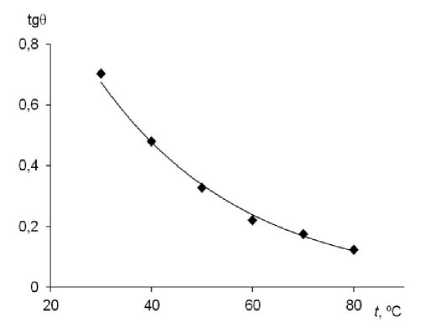
Рис. 1. Зависимость тангенса угла механических потерь tg θ от температуры для ПЭС-2

Поскольку значения тангенса угла механических потерь tgθ с увеличением температуры уменьшаются, то частота релаксации отдаляется от частоты сдвиговых колебаний. Для того чтобы приблизиться к f рел , необходимо проведение экспериментов при более низких температурах.

На основе сходства между акустическим поведением сильновязких жидкостей и микронеоднородных сред Исакович и Чабан [15] предложили релаксационную теорию, согласно которой сильновязкая жидкость является микронеодно-родной двухкомпонентной средой, состоящей из динамических упорядоченных и неупорядоченных областей. Эта теория успешно объясняет аномальное поглощение и дисперсию скорости звука в сильновязких жидкостях.

Исходя из этой и аналогичных моделей [16-19], полагаем, что динамическая структурная микронеоднородность характерна для всех жидкостей и аморфных сред. Между сильновязкими и маловязкими жидкостями существует лишь количественное различие, время жизни микронеоднородностей в маловязких простых жидкостях существенно меньше, чем у сильновязких [5]. Низкочастотную релаксацию в жидкостях можно сравнить с медленным процессом λ — релаксации в аморфных полимерах, который наблюдается выше температуры их стеклования и объясняется распадом физических микрообъемных узлов — ассоциатов молекулярной сетки [18, 19]. Низкочастотная вязкоупругая релаксация жидкостей обусловлена распадом и восстановлением кластеров, состоящих из большого числа связанных молекул, природа которых является флуктуационной. Распад кластера представляет собой многоступенчатый процесс перехода связанная молекула — свободная молекула и характеризуется большим временем релаксации τ .

Как и в случае λ-процесса релаксации в аморфных полимерах, можно полагать, что энергия активации низкочастотного релаксационного процесса U не зависит от температуры. Она характеризует энергию сцепления между кластером и возбужденной кинетической единицей, ответственной за элементарный акт релаксационного перехода с временем релаксации [5]:

τ = В λ exp(U/kT), (5) где B λ — предэкспоненциальный множитель для низкочастотного релаксационного процесса. В аморфных полимерах наблюдается большое разнообразие упорядоченных микрообластей, играющих роль микрообъемных физических λ -узлов, и в соответствии с этим в них возникает не один, а целая группа λ -переходов с одинаковыми энергиями активации, но с разными коэффициентами B λ [18, 19].

Рассматривая время релаксации τ как величину, обратную частоте релаксации τ = 1/ f рел , которой соответствует максимум механических потерь, определим значения τ ( Т ) при разных температурах. Величину f рел ( Т ) найдем по данным о температурной зависимости тангенса угла механических потерь tgτ с помощью соотношения (4).

Линейная зависимость lnτ от обратной величины температуры (1/ Т ) (рис. 2) подтверждает экспоненциальную температурную зависимость времени релаксации (5) для полиэтилсилоксановой жидкости ПЭС-2. Отсюда получаем следующую оценку энергии активации низкочастотного релаксационного процесса ( R — газовая постоянная)

и = /?[Д/пт/Д(1/Т)] ≈ 26 кДж/моль.

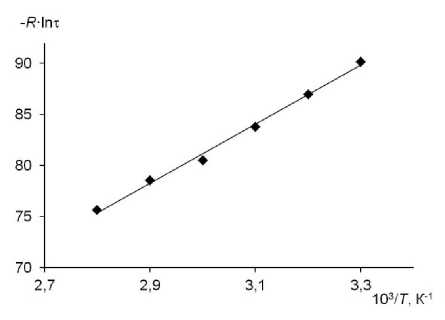
Рис. 2. Зависимость R ·lnτ от обратной величины температуры Т для ПЭС-2

Полученный результат свидетельствует о том, что низкочастотный процесс релаксации в полиэтилсилоксановых жидкостях относится к низкоактивационным процессам и согласуется с представлением, что полиорганосилоксаны обладают механическими и реологическими свойствами, которые связаны со слабым межмолекулярным взаимодействием и с высокой гибкостью полимерной силоксановой цепи [13]. В дальнейшем для более надежного определения энергии активации и коэффициента B λ необходимо провести измерения внутреннего трения жидкостей при разных частотах и температурах, как в физике полимеров [18, 19].

Физико-механические свойства некристаллических твердых тел определяются во многом структурой жидкости, которая фиксируется в области стеклования [20-24]. В модели делокализованных атомов [25-27] элементарным актом пластической деформации стекол служит молекулярный механизм вязкого тече- ния расплавов этих систем [26, 27]. Обращает внимание то обстоятельство, что энергия активации низкочастотного релаксационного процесса в полиорганоси-локсановых жидкостях совпадает с энергией делокализации атома Δε ≈ (20–25) кДж/моль в силикатных стеклах и их расплавах с силоксановыми связями [28, 29]. Процесс делокализации атома в них представляет собой предельное смещение «шарнирного» мостикового атома кислорода в мостике Si–O–Si, связанное с локальной низкоактивационной деформацией кремнекислородной сетки. Поэтому исследование природы вязкоупругих процессов, в частности, механизма вязкого течения жидкостей представляет интерес для решения проблемы эффекта пластичности стекол.

Заключение

Проведенные исследования полимерных жидкостей наряду с предыдущими работами [3, 5-12] подтверждают представление о том, что все жидкости независимо от их природы обладают низкочастотной сдвиговой упругостью. В соответствии с кластерной моделью она обусловлена распадом и восстановлением относительно долговечных динамических упорядоченных областей структуры, природа которых является флуктуационной: с течением времени они образуются и распадаются. Распад происходит путем перехода связанная молекула — свободная молекула и характеризуется большим временем релаксации и, следовательно, низкой частотой перехода. Считая время релаксации величиной, обратной частоте релаксации, которой соответствует максимум механических потерь, установлена экспоненциальная температурная зависимость времени релаксации τ( T ), откуда определена энергия активации низкочастотного релаксационного процесса для полиэтилсилоксановой полимерной жидкости: U ≈ 26 кДж/моль. Следовательно, низкочастотная вязкоупругая релаксация в полимерных (и, возможно, в других) жидкостях относится к низкоактивационным процессам.

Развивается представление о том, что низкочастотная вязкоупругая релаксация в жидкостях по природе аналогична λ -процессам релаксации в аморфных полимерах, которые наблюдаются выше их температур стеклования и связаны с распадом и восстановлением микрообъемных физических узлов молекулярной сетки.