Низкочастотные сдвиговые волны в жидкостях

В работах [1-2] акустическим резонансным методом с применением пьезокварцевого резонатора была обнаружена и в дальнейшем всесторонне исследована сдвиговая упругость из обычных жидкостей при частотах сдвиговых колебаний порядка 105 Гц [3-9]. Суть акустического резонансного метода заключалась в следующем. Боковая горизонтальная поверхность пьезокварца соприкасается на одном конце с прослойкой исследуемой жидкости, накрытой твердой накладкой (рис. 1).

Накладка механическими приспособлениями может перемещаться по вертикали, чем регулируется толщина жидкой прослойки в широких пределах. При тангенциальных смещениях грани пьезокварца прослойка жидкости испытывает деформации сдвига и в ней должны установиться стоячие сдвиговые волны. В зависимости от толщины жидкой прослойки изменяются параметры резонансной кривой пьезокварца: резонансная частота и ширина резонансной кривой. Максимум затухания сдвиговой волны будет наблюдаться при противофазе прямой и отраженной от накладки волны. Таким образом, можно осуществить ультразвуковой интерферометр на сдвиговых волнах в жидкостях.

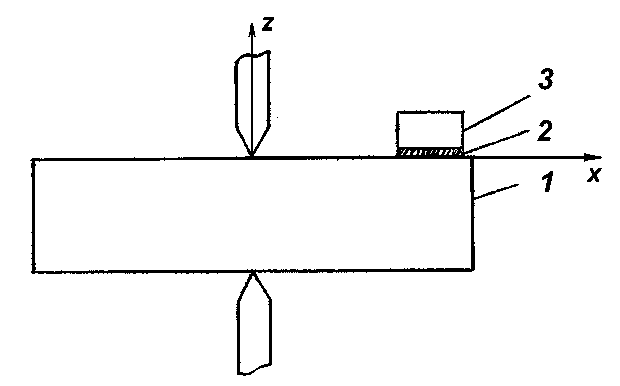
Рис. 1. Пьезокварц с добавочной связью: 1– пьезокварц, 2 — прослойка жидкости, 3 — накладка

Теория акустического резонансного метода [5] дает для комплексного сдвига резонансной частоты пьезокварца массы М следующее выражение:

Δ _{f *} = S χ G * ⋅ 1 + cos(2 χ * H -ϕ *) 4 π ² Mf ₀   sin(2 χ * H - ϕ *)

где G* = G'+iG''– комплексный модуль сдвига жидкостей, S — площадь основания накладки, χ* — комплексное волновое число, Н — толщина жидкой прослойки, f0 — резонансная частота, φ* — комплексный сдвиг фазы при отражении волны от границы жидкость-накладка. Учитывая, что накладка из-за малой величины связи, осуществляемой прослойкой жидкости, практически покоится (φ* = 0), для действительной Δf' и мнимой Δf '' частей (1) можно получить:

S ⋅ ( G ' β+ G '' α )sin2 β H + ( G ' α- G '' β )sh2 α H 4 π ² Mf ₀ ⋅            ch 2 α H - cos2 β H

S ⋅ ( G ' β+ G '' α )sin2 β H + ( G '' α+ G ' β )sh2 α H 4 π ² Mf ₀            ch 2 α H - cos 2 β H

Отсюда следует, что зависимость и действительного и мнимого сдвигов частот от толщины жидкой прослойки должны давать затухающие осцилляции. При этом первый максимум затухания будет располагаться на расстоянии равной половине длины сдвиговой волны в исследуемой жидкости. Используя соотношение (χ*)2 = ω2ρ/G*, из выражения (3) можно получить фор- мулу для расчета действительного модуля сдвига в виде:

G ' = λ ² f ₀ ² ρ cos θ cos² ( θ /2),

где f₀ — резонансная частота пьезокварца, р — плотность исследуемой жидкости, 9 — угол механических потерь. Значение tg 9 определяется измерением расстояния А Н между положениями первого минимума и максимума действительного сдвига частоты [5]. Из теории метода каждому значению А Н/ к соответствует определенное значение tg 9 . Таким образом, для определения G ' и tg 9 достаточно измерить длину сдвиговой волны к по положению максимумов затухания и расстояние А Н .

В эксперименте применялся пьезокварц Х-18.5 ° среза, у которого по литературным данным на рабочей поверхности коэффициент Пуассона равен нулю. Поэтому прослойка жидкости подвергалась чисто сдвиговым деформациям. Резонансная частота пьезокварца составляла 74 кГц. Были исследованы различные жидкости: спирты, гликоли, гомологические ряды углеводородов и полимерных жидкостей. Проведенные исследования показали, что особое значение для воспроизводимости результатов измерений имеет тщательная очистка рабочих поверхностей, обеспечивающая ее хорошее смачивание. Лишь «прочное сцепление» жидкости с рабочими поверхностями способно устранить явление проскальзывания между ними в процессе колебания пьезокварца. В противном случае из-за скольжения жидкости по поверхностям контакта отраженная от накладки волна приходит обратно на разные участки пьезокварца с различными фазами, и осцилляции сдвигов частот значительно сглаживаются.

Экспериментальные результаты и обсуждение

В данной работе приведены результаты исследования полиэтилсилоксановой жидкости, которая является поверхностно-активной. На рис. 2 показаны экспериментальные результаты для ПЭС-3. Кривая 1 относится к действительному сдвигу частоты, а кривая 2 — к мнимому. Из рисунка следует, что для ПЭС-3 длина сдвиговой волны λ = 298 мкм. По формуле (4) для ПЭС-3 G ‘ = 3,1 - 10 6 дин/см². По значению А Н / к определено значение tg 9 и оно равно 0,87. Для этих значений модуля сдвига и угла механических потерь по формулам (2) и (3) были рассчитаны теоретические зависимости А f ’ и А f "  от толщины прослойки жидкости (сплошные на рис. 2). Видно, что экспериментальные кривые достаточно хорошо соответствуют теоретическим.

В работе [6] приведены результаты измерения G' полиэтилсилоксановой жидкости (ПЭС-3) акустическим резонансным методом при условии, когда толщина жидкой прослойки H много меньше длины сдвиговой волны λ. В данном эксперименте накладка достаточно малой массы свободно накрывала тонкую прослойку исследуемой жидкости. При этом рассчитанное значение модуля сдвига G‘ для ПЭС-3 составила 3,45-106 дин/см2. Видно, что значение G', полученное данным методом, несколько больше значения, полученного на ультразвуковом интерферометре с жестко закрепленной накладкой. В реальных кристаллах, несмотря на выбор подходящего среза (Х-18,5°) всегда существуют нормальные колебания. Поэтому при колебаниях пьезокварца исследуемая прослойка жидкости испытывает, кроме сдвиговых, дополни- тельные деформации сжатия и растяжения. Этим объясняется некоторое различие полученных разными способами результатов.

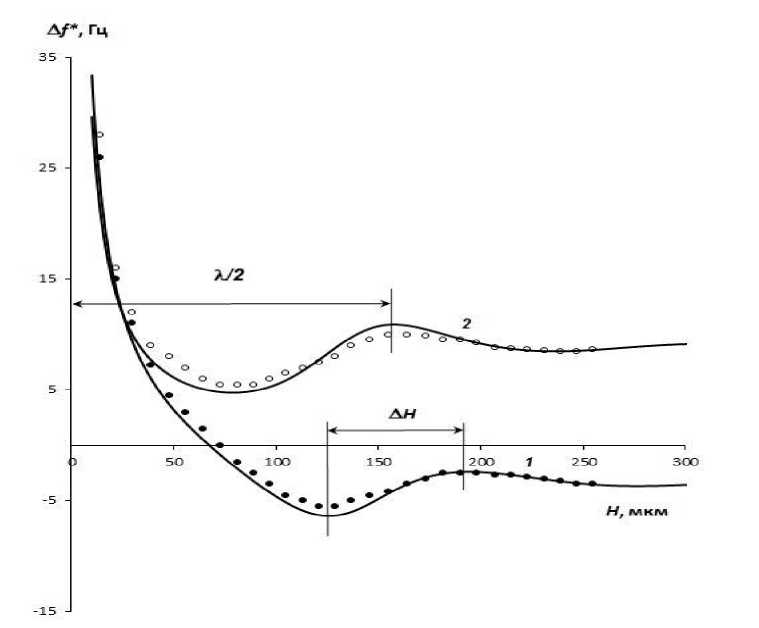
Рис. 2. Зависимости теоретических (сплошные линии) и экспериментальных (точки) сдвигов частот от толщины жидкой прослойки для ПЭС-3: 1 — действительный, 2 — мнимый сдвиги частот.

Работа выполнена в рамках государственного задания ИФМ СО РАН и частично поддержана грантами РФФИ (проект № 15-42-04319-р_сибирь_а, № 15-02-08204-а).