Noisy Image Decomposition Based On Texture Detecting Function

Published Online April 2012 in MECS DOI: 10.5815/ijigsp.2012.03.03

Image decomposition is only a class of image processing which is between the middle-level image processing with low-level image processing or image analysis, but also plays an important role in middle-level image analysis and high-level image understanding or computer vision. Given f (x), for simplicity, is denoted by f , where x = (x1, x2)T is a vector in domain Q . Let f be an observed image contained texture, such as f = u + v , where the first component u represents cartoon part, with some simple geometric description, the second component v is oscillating part included texture and/or noise, i.e. v = f - u . The main aim of image decomposition is to separate cartoon part u and texture, or noise part v from an observed image f . Recently, many researches have proposed many PDE- methods for noise-free image decomposition; see, such as AABC model[2], LJL model[10], ROF model[13], and other models[6,9,11,14-15]. In this paper, they will mainly offer an image decomposition method for partly noisy images. However, the noisy image decomposition task is still challenging and important.

In 1992, Rudin et al.[13] presented the ROF model to denoise. The model is

min E(u) = |nlDu + ^lu - f IlL2(q) .

where X is a positive constant, Q is a domain. As we know, this model performs very well for image denoising, and preserves some details, such as, edge, texture, etc. On the one hand, since the TV regularization term is isotropic diffusion, the ROF model will lead to block effect and over-smooth, for example, small details, such as texture, are destroyed if the parameter X is too small, the other is the function u , which is a function of bounded variation(BV), belonging to BV space. As we know, BV space ensures the regularity of solutions and non-continuity of some regional, it is an ideal space for image processing. The regularization term | | Du | can be defined as follows:

Ф п ) * C 0 ( Q ) N } .

Jq| Du| = sup {| udivpp = (ф1, Ф2,---, where ||ф|L,(Q) < 1. But it is difficult to find such a function ф when they take the numerical implementation. So, in the numerical implementation, they transfer the regularization term | |Du| into |q|Vudx , which is to say, u belongs to the Sobolev space, which causes the inconsistency between the theoretical model and numeri- -cal simulation.

In 2011, Liu et al.[10] proposed a new image decomposition model by using a dual method inspired by [3]. The model can be described as min E(u, w) = Jq IVwdx + 911w - u||L2 (Q) + " ||f - u||L2 (Q).

show the existence of minimal solutions of their proposed model. In section IV., they show some experimental results. In section V., they give some discussions and conclusions.

They call overcomes model and function w proved the

this model as LJL model. This model the inconsistency between the theoretical numerical simulation by introducing a new in Sobolev space. At the same time, Liu also existence of solutions of minimal functional

model, and show that the LJL model works very well for image decomposition of noise-free images. The results of their proposed model in this paper will be compared them with those of LJL model.

In 2009, Li et al.[9] designed a variational denoising model for partly textured images by introducing a texture detecting function in the ROF model. The model is to minimize the following energy functional min E (u) = JQ | V u|dx + у Jq(1 - g)(u - f )2 dx. where g is a texture detecting function according to the derivatives of the noisy image with texture. Li used the idea of total variation(TV) flow to remove the noise, that is,

5f      I Vf 1

= div .

dt      ^Vf\ J

And then, they offered to extend the structure tensor by using the first and second order derivatives to extract the texture feature in a noisy image. The six feature channels are as follows

II. Proposed Model and Algorithm

In this section, they develop a new model for noisy image decomposition. Based on the advantages of the texture detecting function[9], they are to minimize the following energy functional muin E(u,v )=fn g\Du\+" L(1 - g)v 2 dx

+Ц JQ(f - u - v )2 dx.

where "  and ц are two positive constants. u e BV ( Q ) is cartoon part of f , v e L ( Q ) is texture component, n = f - u - v e L ( Q ) is noise component.

Since there is the regularization term |_q | Du | in the above energy functional, as aforementioned, in order to overcome the inconsistence shortcoming of theoretical model and implement algorithm, they are more willing to propose the following model inspired by the dual method [3,10],

min E ( w , u , v )

w , u , v

=L g l^V w dx+2 5 J „ ( w - u ) ’ ^dx

(2.1)

u 1 = ^f2

u 2 = ^fx 2

u = f 2 , u = f 2 4 x ₁ x ₁ 5 x ₂

u₃ = f f , 3 x ₁ x ₂

^U 6 = ^fx 2 .

+"

2 Jq

Ц Jq(f - u -v )2 dx.

Since the noise in f is amplified by taking derivatives, they again used the TV flow to denoise each part u_i , i.e.

dut        Г Vut 1 .

—- = divh—4 , i = 1,^,6.

dt        (|V ui.|J and provided a texture detecting function as

g ( x 1 , x 2 ) =

1 + k Л ² ( x 1 , x ₂ )

where k is a positive constant and Л ( x 1 , x ₂ ) is the largest eigenvalue of the geometric matrix

1+К( u) x,,

К Ui) x1( Ui) x2

.

K ⁽ u i) x 1 ⁽ u^ x ₂ ,

1+K u)!

where " , 9 and ц are three positive constants, w e W ^1,1 ( Q ) , u e L ² ( Q ). The others are the same as the above. The first and the second terms are the test and approximation terms on cartoon part u , respectively. The third term is the test term on texture component v , and the fourth term is the data-fidelity component, or noise component. According to the definition of the texture detection function g e (0, 1), they can see that the first term plays more roles when g tends to one in the cartoon domain, and the third term takes more important part when g goes to zero in the texture or noise domain.

In order to solve the minimal solutions of their proposed model, they can first compute the Euler-Lagrange equations. And then, they use the steepest descent method to find the evolvement equations. There are as following

From the above construction, they can see that each component of u is near zero such that g goes to one in the homogeneous regions; at least one component of u is very large such that g goes to zero in the regions with texture or noise.

The rest of the paper is organized as follows. In section II., they construct a new noisy decomposition model and write out the execution algorithm. In section III., they

dw

— = div d t

(2.2)

w + 9ц( f - v) u =----------------,1 + 9ц

ц( f - u) v =----------—.

ц + " (1 - g)

(2.3)

(2.4)

In this paper, they follow the alternating iterative algorithm to implement the above evolution equations, the alternating minimization algorithm is running in the order of ( 2.2 ) ^ ( 2.3 ) ^ ( 2.4 ) ^ ( 2.2 ) ^ ( 2.3 ) ^ ( 2.4 ) ^ . They will employ pseudo-codes to write down the specific steps in the following.

Firstly, they compute the texture detecting function g .

• (1)    Denoising a noisy image f by TV flow

Initialize u ⁽⁰⁾ = f, т = т 0 (time step, Default 1).

For n (iterations, Default 20)

u ⁽ " ^{+ 1)}

End

They can get denoising result u_End ^ I . If the image is a noise-free image, they just take n = 3.

• (2)    Denoising the six channels using TV flow

Initialize т = т0 (time step, Default 1), u. = 12 , u-, = 12 , щ = I I ,

1 x ₁2 x ₂3 x ₁ x ₂

they relax the energy functional(2.1) into the following form:

i w i i n E ^{£ (} w , u , v ) = f _n g i^v wdx ⁺^i w - u L 2 _(n)

+X J^1 - g)v 2 dx+£\If- u - vl L и

+£ L(w 2+IV w2 )dx.          (3Л)

where v e L ² ( Q ) , u e L ² ( Q ) , w e W^1,2 ( Q ) .

Proposition 1 Fix £ >  0 , there is a minimal solution ( w ^£ , й ^£ , v ^£ ) of the problem (3.1), where ( w ^£ , й ^£ , v ^£ ) in W ¹¹² ( Q ) x L ² ( Q ) x L ² ( Q ) .

Proof: Fix £ >  0, it is clear that E ^£ ( w , u , v ) is coercive. Let ( w £ , u £ , v £ ) be a minimizing sequence for the problem(3.1), then they can obtain that there is a generalized positive constant M such that

E^£ (w ^£ , u ^£ , v ^£ ) = f g I V w ^£ dlx + — II w ^£ - u ^£ 1 1²,

V ^{n n} "' Jn⁶l ⁿ l 2 0 II ^{n n} I L ² ( q )

u, = 1 L , u^ = I , u₆ 4 x ₁ x ₁ 5 x ₂ x ₂ 6

For n (iterations, Default 2)

(   (

= 12

.

⁺ £ J q ^{( 1 -} g ^{) ( v}" ^{) 2 dx +} £\ I f ^{- u}-

v " I L ² ( Q )

( " + 1) , ( u ( ’ ^ u (

+ т div

V u’"’

| V u i" )|

.

⁺ £ J _Q ( ( ^w£ ) ²⁺ 1 ^{V w}" I² ) d ^x - M .

End

(3) Computing the detecting function g .

Secondly, they decompose the noisy image.

Initialize u ⁽⁰⁾ = z , v ⁽⁰⁾ = u ⁽⁰⁾ - 255 g , w = u ⁽⁰⁾ , т = т 0

Then,

I w £ - u£\\_{6 M}< M , I f - u .- ^- vr||L . ₍ „ , ^- M ,

L ² ( Q )

Hence, they have

^- M , ll^V » ^£ I L ._W1 ^- M .

(time step, Default 2), k = k 0 (positive constant, Default 5 x 10 - 4 ), X = X ₀, ц = ц ₀ (two positive parameters,

^{1L 2} ( ^Q )

L -m, ||w„£||      -m.

I L ² (Q)             II "  I W ¹¹²(Q)

Default 0.01), 0 = 0 ₀ >  0 (Default 0.1), £ = £ ₀ (Default 1 x 10 ^{- 5} ).

For n (iterations, Default 20)

That is to say, they get that w £ , u £ and v £ are bounded in W ^1,2 ( Q ) , L ² ( Q ) and L ² ( Q ) , respectively. So, there exist iw ^£ , й ^£ and v ^£ in W ^1,2 ( Q ) , L ² ( Q ) and L ² ( Q ) ,

w ⁽ " ^{+ 1)}

(   (

’⁽ " ’ + т div •

w ⁽ u ^{( n + 1)}

g V w ⁽ " ’ | V w ⁽ " )| + £ 0 ,

,( " ^{+ 1)} -A.- _

т 1 ( w ⁽ " ’ -

u ⁽ " ’ )'

,

1 + 0ц

_v ( n ■ ^ Ц ⁽ f - u ⁽ " ^{+ 1)} ) .

X(1 - g ) + Ц

,

and three subsequences such that w £ ^ iw ^£ in W ^1,2 -norm, u £ ^ й ^£ in L ² -norm and v £ ^ v ^£ in L ² -norm, respectively. According to the convexity, they gain that ( iw ^£ , 11 ^£ , v^{2 £} ) is a solution of problem (3.1).

Proposition 2 Fix £ >  0, if ( iw ^£ , u ^£ , v ^£ ) are minimal

End

After running, they can receive the results of image decomposition by their proposed model, which include cartoon part u ^ u_End , texture/noise part v ^ v_End , and residual part . ^ f - u - v .

solutions of problem(3.1), then they separately satisfy the Euler-Lagrange equations

- div

( g V iw ^£

JV , !■- I

+ — hr 0V

-11£ ) + £lw£ - £Alw£

= 0,

(3.2)

III. Existence of Minimal Solutions

In this section, they prove existence of minimal solutions of their proposed energy functional model. Now,

- 1(!w ^£ - 11 ^£ ) - ц ( f - й ^£ - v ^£ ) = 0,         (3.3)

X (1 - g ) v ^£ - ц ( f - u ^£ - v ^£ ) = 0.          (3.4)

dw with the Neumann boundary condition, —— = 0 . dN

Proposition 3 Fix e > 0, if f e L (Q) and (vE,U)E, vE) are minimal solutions of problem (3.1), there are two constants a, b such that k0 = ess inf f < vE < ess sup f = k1, Q               Q k0 = ess inf f < йE < ess sup f = k1, b < vE < a.

^Q               Q

Proof: Let k1 = ess sup f, G e C1 (Q) is a truncation Q function, G(t) = 0 on (-”,0] , and G(t) is strictly increasing on (0, +”) . Given z = G(vE - k1), and then Vz = G (vE - k1) ■ VvE. They multiply equation (3.2) by z and integrate in Q , then they can get

Jqg|vvE|■ G‘(vE -k1 ^с + 9 Jq(vE -йE)■ G(vE -k1 )dx +eJq vE ■ G(vE -k1 )dx + eJQvvE| ■ G‘(vE -k1 )dx = 0.

Since G >  0, g e (0,1) and G >  0, they must satisfy

-J( v ^E - й ^E )■ G( v ^e - k^x + E v ^E ■ G( v ^E - k^x <  0. (3.5) ⁹ Q^v                          Q

Theorem 1 Let f e L ” ( Q ) , then there is at least one minimal point ( iv, й,v ) in BV ( Q ) x L ( Q ) x L ( Q ) , such that E ( v , u , v ) of the functional(2.1) reaches its minimum at point ( i v , Ui, v ) .

Proof: Based on the above discussions, they have

E ^E ( » ^e . ^{u e} . v ^E ) = / „ g ^ -!■ ^e lx + 2 9 1 v ^e - ^{u e}| L _м

+ 2 j ( i - g ) ( v ^E ) 2 dx + ц| f - ^uE - v e i’,„,

+ 1 j = (⁽ ' i ^{e ) 2+}i^{v v e} i² ) d ^x

• < E ^E ( v , u , v )

• = J q g ^V ^Vx ⁺ 71 9 I к ^{- U} | I L 2 ( Q )

+ 2 Jq(1 - g) v2dx + Цlf -u - vlL2(Q)

+E Jq( w 2+iv v 2) dx.

i.e.

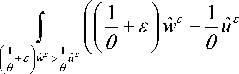
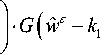
for all w e W ^1,2 ( Q ) , u e L ² ( Q ) , v e L ² ( Q ) . Especially,

they take v = 1, u = 1, v = 1, then

II^{v vE} l 1 1_Ю)

< " , l’^{!i E} lL1(„, < " ,

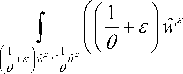
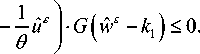
II ^uE lL._M)< " , HL._M)< " .

Thus, if and only if there is

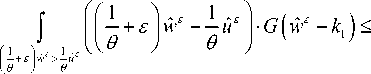
The inequality (3.5) is always set up. In fact, it is equal to zero since G >  0. Therefore,

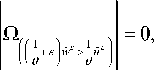
where (| is Lebesgue measure, then,

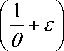
; e

EE v <  — u ,

.; E

and v ^E <  й ^E .

According to (3.3) and (3.4), they have

They can receive that i v ^E is uniformly bounded in W ^1,1 and BV space. Thus there exists a subsequence i v ^E n and i v in BV space such that i v ^E n ^ i v in BV- v * and i v ^E n ^ i v in L -norm. At the same time, й ^E and i)^E are uniformly bounded in L ² space, then there are also two subsequences й ^E n , v ^E n and z), v ⁵ in L ² space such that й ^E n ^ й in L -norm and v ^E n ^ v in L ² -norm, where E n ^ 0 , if n ^ ” . According to the convexity, they get E ( v , u , v )

< liminf E ^E ( i v ^E n , й ^E n , v) ^E n ) n ^”

= liminf < [ g Vi v ^E n lx + — lli v ^E n - й ^E n II, n ^” iJq⁶! I 2 9 II I L ² ( q )

1 + 9ц

v ^E + 9ц\ f -

ц(f - uE) ) Ц + 2(1 - g) J

Furthermore, they derive

e 2(1 - g) f + циЕ u <

Ц + 2(1 - g)

.

Therefore, they get й ^E <  k 1 . Similarly, they can get k ₀ = ess inf f <  U ^E , k ₀ = ess ii i f f <  v ^E .

According to (3.4), they get v = Ц( f - Ui e )

Ц + 2(1 - g)

Since k ₀ <  U ^E <  k 1 , they have b = - 2 k ₀ <  v ^E <  2 k 1 = a .

+2 Jq(1 - g)(v En )2 dx+^21 lf - u)En

-

E г / /        \2 I |2 \

+ I n "J _Q ((ⁱ v ^E n ) +|vⁱ v ^E n l )

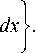
So, ( i v , Ui, v ) e BV ( Q ) x L ² ( Q ) x L ² ( Q ) is a minimal solution of the minimization functional (2.1).

• IV. Numerical Experiments

In this section, they show some numerical results by their proposed model in the following, and compare them with some results by LJL model[10]. In the following experiments, they take zero-mean Gaussian noisy images with variance ст2 = 0.01.

(c)

Figure 1. Decomposition of the noise-free Logo image. (a) Logo image, (b) Cartoon part of their proposed model, (c) Texture part of their proposed model, (d) Texture detecting function, (e) Cartoon part of LJL model[10], (f)Texture part of LJL model[10].

(a)

(c)

(d)

(a)

(e)

(f)

(e)

(f)

Figure 2. Decomposition of the noise-free Badge image. (a) Badge image, (b) Cartoon part of their proposed model, (c) Texture part of their proposed model, (d) Texture detecting function, (e) Cartoon part of LJL model[10], (f) Texture part of LJL model[10].

Figure 1-2. show the decomposition results of the Logo image and Badge image without noise. Texture detection functions in Figure 1-2.(d) work well for searching the border and texture of noise-free images. Comparing Figure 1-2.(b) with Figure 1-2.(e), respective -ly, you can see that the cartoon parts of their proposed model are less geometry and texture details than those of LJL model. However, it is regret that there is oversmooth in some parts of Figure 1-2.(b). Similarly, com-paring Figure 1-2.(c) with Figure 1-2.(f), respectively, they can get that the texture parts of their proposed model are richer than those of LJL model[10].

(e)

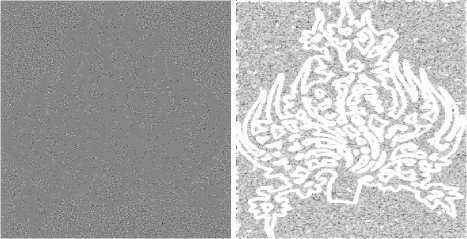
Figure 3. Decomposition of the noisy Logo image. (a) Noise-free Logo image, (b) Noisy Logo image, (c) Cartoon part of their proposed model, (d) Texture part of their proposed model, (e) Residual part or noise of their proposed model, (f) Texture detecting function.

№S

ЫЗУ • f > , ^fo’^ -4, #?*^‘^

(f)

(b)

(e)

(f)

Figure 5. Decomposition of the noisy Flower image. (a) Noise-free Flower image, (b) Noisy Flower image, (c)Cartoon component of their proposed model, (d) Texture part of their proposed model. (e) Residual part or noise of their proposed model, (f) Texture detecting function.

fWfiDO 3MT COM I

(e)

(f)

Figure 3-5. show the decomposition results of the Logo image, Badge image and Flower image with Gaussian noise. By observing the cartoon parts of Figure 3-5.(c), you can see that the cartoon parts are decompos--ed well for the noisy Logo, Badge and Flower images. In the same way, you can know that the texture parts are largely separated from the noisy Logo, Badge and Flower images by analyzing Figure 3-5.(d), but Figure 3-5.(d) contain a part of noise component. Texture detection functions in Figure 3-5.(f) basically identify the texture parts of noisy images, but also include a fraction of the edge of noise. Residue part in Figure 3-5.(e) don't involve texture or cartoon, that is, its are truly noise.

Figure 4. Decomposition of the noisy Badge image. (a) Noise-free Badge image, (b) Noisy Badge image, (c) Cartoon component of their proposed model, (d) Texture part of their proposed model. (e) Residual part or noise of their proposed model, (f) Texture detecting function.

(a)

V. Conclusion and Discussions

In this paper, they have proposed a new model for noisy image decomposition based on dual method and a texture detecting function. Simultaneously, they also prove the existence of solutions of the minimal functional (2.1). From the numerical simulations, you can see that their proposed model not only processes well for noise-free images, but also deals well with images with Gaussian noise. However, they can't entirely decompose texture and noise for noisy images, see Figure 3-5.(d). Additionally, their proposed model can only deal with Gaussian noise image with small variance. In the case of large variance, the decomposition result of their model is not satisfactory. Therefore, further study will focus on these problems, for example, How to completely separate texture and noise, noisy images with large variance, and so on.

Acknowledgements

This work is supported by National Science Founda--tion of China(10971239), Natural Science Foundation Project of CQ CSTC (CSTC2011JJA40033, CSTC2010--BB2310), CQUT foundation (2010ZQ13).

(c)

(d)