Номинальная программа управления сближением космического аппарата - сборщика мусора с электроракетным двигателем малой тяги на геостационарной орбите

В настоящее время на околоземных орбитах скопилось большое количество фрагментов космического мусора (ФКМ). Под ФКМ понимаются различные объекты техногенного происхождения в околоземном космическом пространстве – отработавшие свой ресурс космические аппараты, обломки ступеней ракет носителей, разгонных блоков. Все перечисленные объекты имеют достаточно большую массу, параметры их орбиты доподлинно неизвестны. Что в совокупности

перечисленных факторов представляет опасность для действующих и вновь выводимых космических аппаратов.

Орбиты ФКМ можно условно расклассифицировать по типу наиболее востребованных орбит. Однако особенно остро эта проблема стоит для уникальной геостационарной орбиты (ГСО). По некоторым оценкам, среднее расстояние между двумя соседними космическими аппаратами на ГСО составляет величину порядка 500 км, что представляет угрозу для маневрирования действующих космических аппаратов и прохождения радиосигналов на Землю с космических аппаратов, расположенных на ГСО.

Существуют активные и пассивные способы утилизации ФКМ. К активным способам относят создание специальных транспортных средств, так называемых космических аппаратов – сборщиков мусора (КАСМ) [4]. Наиболее рациональным будет оснащение КАСМ электроракетным двига- телем малой тяги (ЭРД). Такой тип двигательных установок обладает высокой скоростью истечения реактивной струи и позволяет совершать транспортные операции в течение длительного времени.

КАСМ может быть как одноразового, так и многоразового применения. КАСМ одноразового применения, после сбора одного ФКМ, затапливается в Мировом океане вместе с собранным ФКМ. Однако, с экономической точки зрения, наиболее рационально использовать КАСМ многоразового применения. Такой тип КАСМ работает по следующей схеме.

КАСМ многоразового применения выводится на низкую круговую орбиту ожидания. По мере поступления команд с Земли, КАСМ совершает перелёт на орбиту ФКМ. Как было отмечено выше, в статье рассматривается утилизация ФКМ с ГСО. Перелёт с низкой круговой орбиты на ГСО рассмотрен в статьях [5-7]. Затем следует этап сближения КАСМ с ФКМ. После того как КАСМ сблизился и зафиксировал ФКМ на своём борту, возможны два варианта дальнейших действий.

В первом случае КАСМ совершает перелёт на орбиту захоронения (круговая орбита выше ГСО). Параметры орбиты захоронения определяются согласно [10]. После чего КАСМ возвращается на ГСО, совершает сближение с другим ФКМ и уводит его с ГСО. Такой цикл повторяется и, по мере выработки топлива, КАСМ возвращается на орбиту ожидания.

Также существует второй вариант. В этом случае КАСМ совершает перелёт на эллиптическую спусковую орбиту с предельно малой высотой перигея. Там КАСМ отсоединяет от себя ФКМ и совершает перелёт на орбиту ожидания. ФКМ входит в плотные слои атмосферы Земли и затапливается в Мировом океане. Такой манёвр рассмотрен в статье [8].

Наиболее сложным является сближение КАСМ с ФКМ. Сближение двух космических аппаратов можно разделить на дальнее наведение, ближнее сближение, причаливание и стыковку.

В настоящей статье рассматривается задача выбора структуры управления сближением на этапе ближнего сближения. Задачей ближнего сближения является приведение КАСМ в некоторую окрестность ФКМ. Здесь важно не допустить столкновения КАСМ с ФКМ. Это означает, что траектория движения КАСМ должна лежать за пределами некоторой сферы безопасности и, кроме того, траектория сближения должна лежать на одной стороне относительно ФКМ.

С другой стороны, движение происходит на основании навигационной информации, поступающей с бортовой навигационной системы КАСМ. Точность этой информации напрямую зависит от расстояния между КАСМ и ФКМ. Поэтому необходимо предусмотреть последовательное приведение КАСМ к границам сферы безопасности.

Как известно, в относительном движении (сближении) можно выделить вековые и периодические составляющие. Задачу управления можно разделить на управление отдельно вековыми составляющими и отдельно периодическими (последовательное управление).

В [9] рассмотрен алгоритм последовательной коррекции вековых и периодических составляющих относительного движения. Сначала происходит коррекция вековых составляющих, затем периодических. В этой статье рассматривается алгоритм совместной коррекции вековых и периодических составляющих относительного движения.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СБЛИЖЕНИЯ

Движение КАСМ относительно ФКМ рассматривается в орбитальной цилиндрической системе координат [1]:

A r = A Vr,

A и = V2-

^^^^^^^^

r ₂

A V r = V ²

V u 1 ^, r ₁

² u 1

l Г ²

Ц

"У ⁺ a S , ^r 1 )

^^^^^^^в

r ₂ r ₁

A V_u = u

^^^^^^^в

r 2 u 2 r 1 u 1

--1⁺ Oy ,

r ₂

r ₁

3 = -^-- ( 1 + e cos 3 ) ². p ³

Здесь A r , A и , A V_r , A V_u — разность параметров движения КАСМ (индекс 2) и ФКМ (индекс 1), V_r 1, V_u 1, V_r 2, V_u 2 - скорость КАСМ и ФКМ в радиальном и трансверсальном направлении, r 1 , Г 2 - радиус орбиты КАСМ и ФКМ, а § и a т — проекции управляющего ускорения на оси орбитальной цилиндрической системы координат, p , e — фокальный параметр и эксцентриситет опорной орбиты, 3— угол истиной аномалии ПКА, Ц — гравитационный параметр Земли. Дифференцирование по времени обозначено точкой.

Смещение АКА относительно ПКА вдоль дуги орбиты ПКА A L через угол A и можно определить:

A L = r 1 - A и , (2)

ФКМ расположен на Кеплеровой орбите, параметры его движения определяются как:

p r1 =              ,

1 + e - cos 3

- e - sin 3 ,

V u 1 =^ p '(1 + e - cos 3 ).

Основываясь на близости орбит КАСМ и ФКМ, уравнения движения могут быть линеаризованы относительно опорной орбиты. Будем полагать,

^{A r} cp = ^^- a T , Х

что в силу малости отклонения по параметрам движения, разностные возмущающие ускорения пренебрежимо малы. В качестве ускорений будем рассматривать проекции управляющего ускорения КАСМ на оси орбитальной цилиндрической системы координат a _S и a _T .

В результате линеаризации и введении допущения о том, что опорная орбита является круговой, уравнения движения примут вид [1, 2]:

А r = A V_r ,

A L = Д V u — Х-Д r ,

₂                   (4)

A V r = 2-Х-A V u + Х - A r + a s , A V = —Х - A V r + a t .

■

A L cp =—1,5-Х-A r cp

—

Х

l = — - (as - sin Ф + 2 - aj - cos ф), Х

Здесь Х = л/ц-(1 - e ) - p

– средняя угло-

вая скорость движения по опорной орбите.

Для проекций управляющего ускорения в соответствии с постановкой задачи можно за-

писать:

a t = a - S, a s = 0.

ф = Х + —— -(as - cos ф — 2 - aT - sin ф).

Х- 1

Граничные условия для задачи сближения АКА с ПКА примут вид:

t = 0:    A r cp =A r cp ⁰,   A L cp =A L cp ⁰,   l = l ⁰,   ф = ф ⁰;

t = t к :   A r cp = 0,        A L cp = 0,        l = 0,    ф = ф к . (8)

Здесь индексы «0» и «к» обозначают, соответственно, начальное и конечное значение рассматриваемого параметра относительного движения.

Сформулируем задачу управления. Для системы уравнений (7) и граничных условий сближения (8), требуется определить зависимость функций включения тяги двигателей (5) от времени.

Здесь 5 — функция включения тяги двигателя в продольной плоскости, которая принимает значение { — 1,0,1 } , a — модуль ускорения от тяги.

Выделим в системе (4) в явном виде периоди-

АНАЛИТИЧЕСКОЕ РЕШЕНИЕ

ЗАДАЧИ СБЛИЖЕНИЯ С МАЛОЙ ТРАНСВЕРСАЛЬНОЙ ТЯГОЙ

ческие и вековые составляющие относительного движения ПКА и АКА. Введём переменные [9]:

Система (7) для управляющего ускорения (5) допускает решение [2]:

2      ⁶

A r (6) = A r 0 — l0-cos (б + ф0)+—-a - JS-(1 — cos(6 —v)) dv, x2    0

„ ( . A V

A г = 2 - A r +---cp l Я

A L ( 6 ) = A L _cp⁰ + 2 - l ⁰ - sin ( й+ф⁰ )

I —

1 e

1,5 -A r _Cp⁰ -й— х a - J s- ( 3 -X- ( 6 — v ) — 4 - sin ( 0 — v ) ) d v ,

,

a V_r ( 6 ) =x- 1 ⁰- cos ( e+ф⁰ ) +| - a

e

J s ■ sin ( e—v ) d v ,

A L cp =A L — 7 'A Vr, Я

e

A V_u ( 0 ) = Х-( l ⁰ - cos ( 0 + ф^o ) — 0,5 -A r _Cp⁰)— — a - J s- ( 1 - 2 - cos ( 0—v ) ) d v ,

l =

tan ф =

^L^ + (A r — A rcp )2, AVr

где 6 = Х - 1 — продолжительность сближения в угловой мере.

Я-A r + 2-A Vu

.

Здесь A r _cp - среднее смещение АКА вдоль радиуса орбиты ПКА, A L _ср - среднее смещение АКА вдоль орбиты ПКА, l – малая полуось эллипса относительного движения КА в плоскости орбиты, ф — угол, характеризующий положение АКА на эллипсе относительного движения в продольной плоскости.

Дифференциальные уравнения относительного движения в рассматриваемых переменных (6) для принятого управления (5) запишутся в виде:

Для переменных A r _cp , Д L с и l уравнения движения примут вид:

2 6

^Д r cp ( ⁶ ) = ^{Д r} cp0 ■ ₂^{- a -}J^S d v ,

^Х 2    0

^{A L} ср ⁽⁶⁾ = ^{A L} ср

^^^^^^в

1,5 - A r cp⁰ -6

—7- a -Х ²

Js-(6 — v) dv,

l2 (6)= 10-sin (6 + ф0 ) + Х2

Js-sin (6 —v) dv

А ²

+

+ 10-cos ^6 + ф )+—2

А ²

Js-cos(6 — v)dv , (10)

0                  J

Введём обозначения K = 2 • —=-, X ²

О

А = !§• sin (О-y) dy,

О

B = |5• cos (О-y) dy,

О

C = |з dy,

О

D = |б^(О-у) dy,(14)

После интегрирования (10), получим аналитическое решение системы (7):

А г ср ( О ) = А Г ср° + K • C,

A L ср ( О ) = А L ср ⁰-1,5•А Г ср ⁰.6-1,5• K• D,                     (15)

1 ² ( О ) = 1 ₀² + 2• K• 1 0 • 7 A² + B² • sin ( О + ф⁰ + ^ ) + K² • ( A² + B² ) .

Задача определения оптимального управления для данной системы является классической [3]. Продолжительности активных участков определятся как:

t ₂

^^^^^^^в

■^+

2        02

t п   ₊ ^Л -^А r cp

V 4      8 • a

+---- cp- • 8 ,

3 • a

t ₁

= t г

- Я •

A r cp

2 • a

• 8 ,

где t 1 и t 2 - продолжительность первого и второго участков соответственно, t _п - заданная продолжительность пассивного участка. Знак ускорения от тяги на первом участке определится как:

8 = sign	АХ 0     Аг 0- Аг 0 ^ А L cp  - я      cP 1 cP 1	. (18)
	3 • a               8 • a
	V                             /

на втором участке знак ускорения от тяги проти-

воположный [9].

B где tan ^ = —

A

Величина продолжительности пассивного участка ограничена. Если она будет слишком большой, то продолжительность первого участка t ₁ станет меньшей нуля, что невозможно. Предельную продолжительность пассивного участка определим из уравнения t ^ >  0, и после преобразований получим:

ФОРМИРОВАНИЕ ПРОГРАММЫ УПРАВЛЕНИЯ ОТНОСИТЕЛЬНЫМ ДВИЖЕНИЕМ

2 •А Lр° max              cp t п = о 1 Ж 0

³ • ^ЛА r cp

^^^^^^^в

А r ⁰

Я --cp- • 8 .

4 • a

Анализ уравнений (7) показывает, что параметры относительного движения А г _ср и A L _ср связаны с параметрами 1 и ф только через управляющее ускорение, что позволяет разделить продольное движение на вековое и периодическое. Вековыми составляющими движения будем считать параметры характеризующие положение центра эллипса относительного движения ( А г _ср и А L _ср ), а периодическими размер малой полуоси эллипса относительного движения и положение КА на нём ( 1 и ф ).

В основу рассматриваемого алгоритма управления положено управление вековыми составляющими относительного движения. Алгоритм управления состоит из двух активных участков ускорения от тяги разного знака и пассивного между ними.

Рассмотрим задачу управления вековыми составляющими относительного движения. Уравнения для А г _ср и А L _ср могут быть приведены к системе стандартного вида:

^ 1 = u ,

X 2 = Х р

Здесь x1 = -1,5• Л-Аrcp, x2 =АLcp, u = 3 • a • 8 , а – модуль ускорения от тяги, 8 = {-1,0, 1} функция включения тяги.

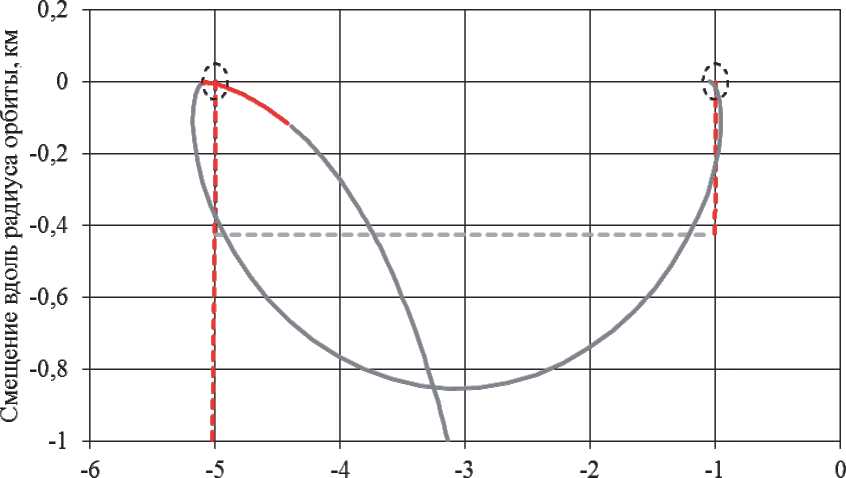
Программа управления (17) обеспечивает удовлетворение граничных условий (8) в части вековых составляющих относительного движения в любом их сочетании. Для удовлетворения граничного условия для малой полуоси эллипса относительного движения, необходимо подобрать такую продолжительность пассивного участка t _п и начальный фазовый угол ф , равные своим оптимальным значениям, которые обеспечивают выполнение условия

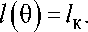
Для определения tп и ф0 воспользуемся аналитическим решением (15). Для программы управления с двумя активными участками зна-копостоянства ускорения от тяги и пассивным между ними (17), интегралы (11) – (14) примут вид:

A = cos ( О-О 1 ) - cos О + cos О 2 - 1, (20)

B = - sin ( 9 - 9 1 ) + sin 9 - sin 9 ₂ ,    (21)

С = О 1 -О 2 ,             (22)

D = ¹ ₂ ² +О _п •О ₁ +О ₂ •О ₁. (23) где 0 = 0 1 + 0 _П + 0 ₂ , 0 1 = Х- t i , 0 _П = Х- t _п и

0 2 = X • 1 2 — продолжительность первого, пассивного и второго участков в угловой мере.

Третье уравнение системы (15), с учётом (20)

и (21) перепишем в виде:

/ \ ²                                                            2

Ш = 1 + 2 • K • V A² + B² • sm 0 + ф ⁰ + ^ ) + K- • ( a ² + B² ) (24)

1 1 о J             l о                                       l о

Для l ( в ) = l к , оптимальная продолжительность пассивного участка t _п определится из нелинейного уравнения:

A ² + B ² = ⁽ l ⁰ ^2к ) . (25)

Для увеличения l ₀ начальный фазовый угол Ф о определится из уравнения:

ф ⁰ = — — 0 — ^ ,            ⁽²⁶⁾

для уменьшения:

ф ⁰ ₌ _|-0-^         (27)

Из уравнения (22) можно определить продолжительность пассивного участка, а из уравнения (23) или (24), для известной продолжительности пассивного участка, начальный фазовый угол, при котором необходимо начинать коррекцию.

АНАЛИЗ ПОЛУЧЕННОЙ ПРОГРАММЫ УПРАВЛЕНИЯ

Возникает вопрос при всех ли комбинациях граничных условий возможна коррекция пара- 00                              0

метров l о , А г ср и А L ср . Параметры А г ср и 0

А L ср могут быть скорректированы при любых граничных условиях и продолжительность коррекции не зависит от l ₀ .

С l ₀ дело обстоит несколько сложнее. Граничные условия по l ₀ ограничены как сверху, 0 так и снизу в зависимости от комбинации А г ср 0

и ^А L ср .

Рассмотрим вариант малых отклонений по А г ср^о и А L ср^о и малой l о . Определим приближённо границу снизу – l ₀^min . Малость l ₀ обуславливает необходимость вводить пассивный участок, по продолжительности близкий к 2 л . Это позволяет максимально уменьшить изменение l ₀ . Тогда можно записать:

0 = 2п + Е + 0 ! +0 ₂,       (28)

где 0 1 , 0 2 и £ — малые величины, так как А г ср ^о и А L ср^о - малы. Получим A = о, B = 0 j — 0 j. Тогда:

l ( 0 ) = l _о — K • B .          (29)

min

Для l ₀     можно записать:

l <7 = K - ( 0 ! —0 2 )

С другой стороны 0 1 и 0 ₂ определяются исходя из требований коррекции А г ср ^о и А L ср^о . Подставив (21) в (29), получим:

I^А Г - “I.

min l ₀

СТРАТЕГИЯ ПРИВЕДЕНИЯ КАСМ В ОКРЕСТНОСТЬ ФКМ

Так как ФКМ является неуправляемым объектом и параметры его орбиты точно неизвестны, то необходимо предусмотреть пошаговый алгоритм сближения. Таким образом, задача сближения КАСМ с ФКМ с малой тягой сводится к следующей стратегии.

Проверка выполнения условия:

l о >  l о™ (32)

Если условие (32) выполнено, то происходит уменьшение малой полуоси эллипса относительного движения. Если условие (32) не выполнено, то происходит увеличение малой полуоси эллипса относительного движения.

Независимо от выполнения условия (32), происходит уменьшение А г ср до нуля, с целью исключения смещения эллипса относительного движения с течением времени. Осуществляется уменьшение А L _ср .

Так как А г ср = о , то l о”^ш = о , следовательно условие (32) выполнено для любой начальной малой полуоси эллипса относительного движения. На втором шаге происходит уменьшение ^А L ср и ¹ .

На третьем шаге осуществляется сближение на расстояние безопасности.

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ

Ускорение от тяги примем равным a =10^-4м/ с². Примем, что КАСМ находится на орбите – большая полуось A = 42489 км, эксцентриситет e = 0,005. Орбиты КАСМ и ФКМ рассогласованы по аргументу широты на А и = 5° .

Переход от параметров орбиты в оскулирую-щих элементах к орбитальной цилиндрической системе координат осуществим по формулам:

А Гср = А A, l = e-А Гср,

А L = r - А и , ср

Ф = 9 ,

где 3 — угол истиной аномалии КАСМ (подбираемый параметр).

Запишем краевые условия сближения на стыковочных участках траектории сближения:

Шаг 1 :	А	r = 327 км, cр	А L ср	- 3680 км,	l = 1,6 км,
	А	Г ер = 0 км,	А L ср =	- 500 км,	l = 39 км,
шаг 2:	А	Г ер = 0 км,	А L ср =	- 500 км,	l = 39 км,
шаг 2.1 :	А А	Г ер = 0 км, Г ер = 0 км,	А L ср = А L ср =	- 100 км, - 100 км,	l = 1 км, (33) l = 1 км,
	А	Г ер = 0 км,	А L ср =	- 5 км,	l = 0,05 км,
шаг 3:	А	Г ер = 0 км,	А L ср =	- 5 км,	l = 0,05 км,
	А	Г ер = 0 км,	А L ср =	- 1 км,	l = 0,05 км.

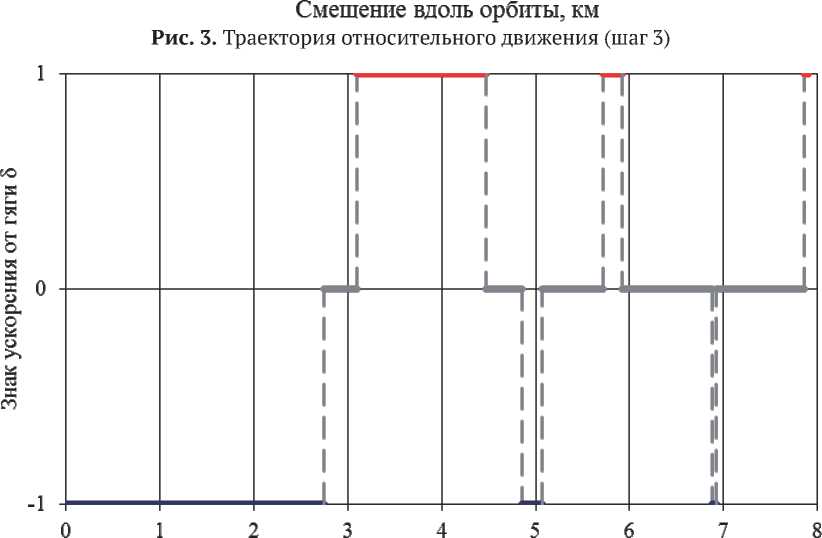
Траектория относительного движения показана на рис. 1, на рис. 2 – 3 покажем траекторию движения на втором и третьем шаге сближения. Расчёт параметров управления осуществлялся численно. Про- должительность пассивного участка определялась из (25) методом хорд и касательных. В качестве начального интервала локализации корня принимался интервал |^0, tnmax J. На рис. 4. покажем циклограмму включения двигателя. Начальный фазовый угол определялся по формулам (26) или (27).

Как видно из рис. 1 – 3, траектория сближения расположена строго левее ФКМ. Как видно из рис. 3, на заключительном этапе ближнего сближения возможная траектория КАСМ (эллипс справа) расположена на достаточном удалении от ФКМ.

Как видно из рис. 4, по мере приближения КАСМ к ФКМ, продолжительности активных

Смешение вдоль орбиты, км

Смешение вдоль орбиты, км

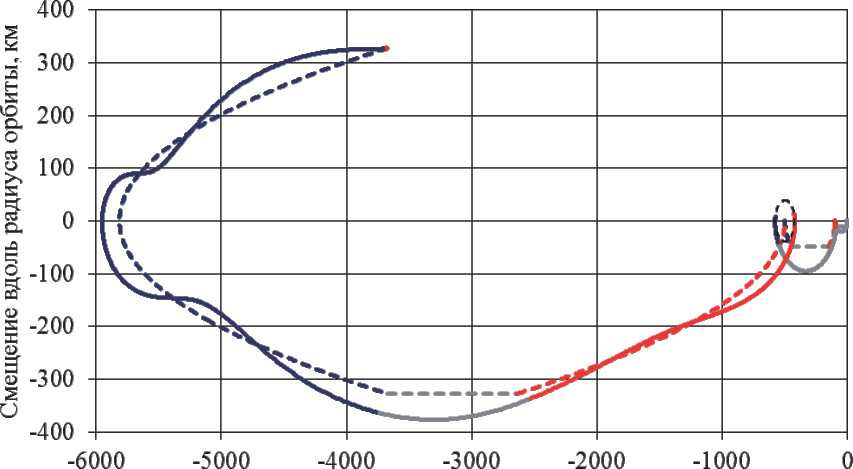
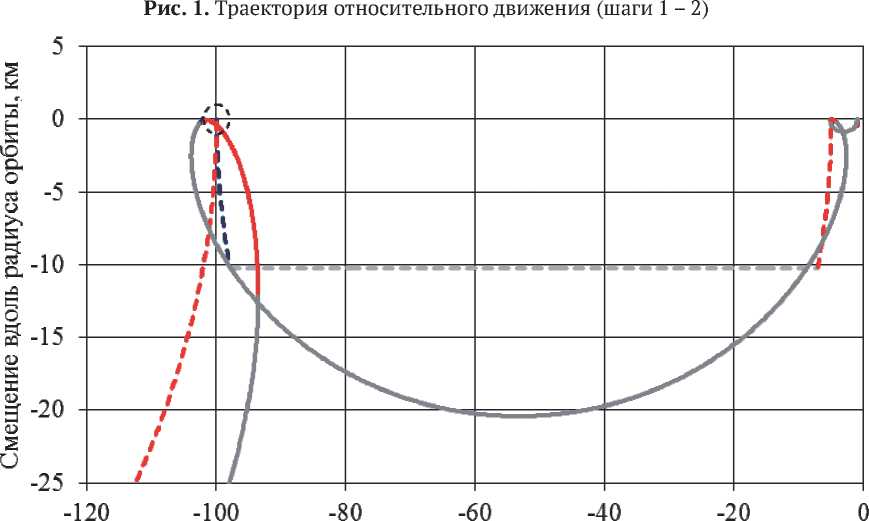
Рис. 2. Траектория относительного движения (шаги 2.1 – 3)

Продолжительность коррекции, сутки

участков уменьшаются, а пассивного увеличивается и стремится к 2·π.

ЗАКЛЮЧЕНИЕ

Рассмотрена задача ближнего сближения космического аппарата – сборщика мусора с фрагментом космического мусора. Относительное движение рассмотрено в орбитальной цилиндрической системе координат. На основании разделения движения на вековые и периодические составляющие, составлен алгоритм управления, состоящий из двух участков постоянства ускорения от тяги, разделённых пассивным. Продолжительности участков и момент подачи первого импульса определяются аналитически.

Для реализации программы управления составлена стратегия сближения. Стратегия предполагает последовательное приведение космического аппарата – сборщика мусора в окрестность фрагмента космического мусора.