Non-parametric multi-step algorithms for modeling and control of multi-dimensional inertia-free systems
Автор: D. I. Yareshchenko
Журнал: Siberian Aerospace Journal @vestnik-sibsau-en
Рубрика: Informatics, computer technology and management
Статья в выпуске: 2 vol.21, 2020 года.
Бесплатный доступ
The paper discusses new classes of models of multidimensional inertia-free systems with a delay in the condi-tions of a lack of a priori information. The subject is multidimensional discrete-continuous processes, the com-ponents of the vector of output variables of which are stochastically dependent in an unknown way. There are also processes, through some channels of which aprior information corresponds simultaneously to both the par-ametric and nonparametric type of source data about the studied process. The mathematical description of such processes leads to a system of implicit nonlinear equations, some of which will be unknown, while others will be known with accuracy to the parameter vector. The main purpose of a model of an object having stochastic de-pendencies of output variables is to find a forecast of output variables with known input variables. To find the predicted values of the output variables from known inputs, it is necessary to solve a system of im-plicit nonlinear equations. The problem is to solve a system that is actually unknown, when only equations for some channels of a multidimensional system are known. Thus, a rather nontrivial situation arises when solving a system of implicit nonlinear equations under conditions when, in one channel of a multidimensional system, the equations themselves are not in the usual sense, and in others they are known accurate to parameters. Therefore, an object model cannot be constructed using the methods of the existing identification theory because of a lack of aprior information. The purpose of this work is the solution of the identification problem in the presence of a partially-parameterized discrete-continuous process, and despite the fact that the parameterization stage cannot be overcome without additional priori information about the process under study. The control algorithm for multidimensional processes with dependencies of output variables is a sequential multi-step algorithmic chain that allows finding the control action and bring the object to the desired state. Computational experiments to study the proposed models and to control multidimensional discrete-continuous processes have shown quite satisfactory results. The article presents the results of computational experiments illustrating the effectiveness of the proposed technology for predicting the values of output varia-bles from known input variables, as well as for managing these processes.
Multidimensional discrete-continuous process, identification, control, T-models, KT-models.
Короткий адрес: https://sciup.org/148321740
IDR: 148321740 | УДК: 519.711.3 | DOI: 10.31772/2587-6066-2020-21-2-215-223
Текст научной статьи Non-parametric multi-step algorithms for modeling and control of multi-dimensional inertia-free systems
Introduction. Consideration and study of multidimensional inertial processes with a delay, which have a stochastic dependence of output variables, is a relatively urgent task. Since such processes are typical for many popular industries, such as metallurgy (steel melting), construction industry (cement production), energy (coal burning), oil refining (increasing the cold flow of diesel fuel) [1], as well as in active systems, such as the educational process (acquisition of knowledge by University students) [2]. Such processes are characterized by the lack of necessary aprior information. The researcher, in such circumstances, should model and manage such multidimensional discrete-continuous processes. These processes are dynamic in nature, but controlled at discrete time intervals, including various ones. Inertia-free systems are considered with known delays, for example, when the object's time constant is 5–10 minutes, and the control of the output variable is measured once every two hours. This leads to the dependence of output variables, for example, in the production of cement, the main output indicator – the activity of cement (compressive strength) depends on another output indicator – the fineness of grinding.
Processes with stochastic dependence of output variables refer to T-processes [3]. The main point here is that the identification of such objects should be carried out in a way that is not traditional for the existing identification theory [4]. There are also cases when aprior information corresponds simultaneously to both nonparametric and parametric types of source data about the studied. Such processes refer to KT-processes [3].
The main feature of T-processes and KT-processes is that the mathematical description of an object is represented as some analog of a system with partially parameterized functions Fj (u, x, a) = 0, j — 1, n and unknown functions Fj (u, x) = 0, j — 1, n . Thus, the identification problem is reduced to the problem of solving a system of nonlinear equations of a partially parameterized discrete-continuous process relative to the components of vector x = (x1,x2,...,xn) , with known values of input variables u = (u1,u2,...,um) . Specific identification tasks will differ in different volumes of aprior information through various channels of the multidimensional process, and in their specific flow.
Researchers have to deal with a system of different types of equations from the point of view of mathematics, the solution of which requires the development of special methods [5]. In this case, it is advisable to use the theory of nonparametric systems [6; 7].
Processes with the stochastic dependence of output variables. As noted earlier, T-processes are multidimensional inertia-free processes with stochastic dependence of output variables. In fig. 1, we consider a multidimensional system that implements the T-process.
In fig. 1 the following notation is used: u = (u1,...,um) -m-dimensional vector of input variables, x = (x1,...,xn) - n-dimensional vector of output variables, ^(t) - random interferences effecting the process. The vertical arrows on the output variables show their dependencies. Through various channels of the multidimensional process, the dependence of the j-th component of the vector can be represented as a certain dependence on certain components of the vector u : x
Such functions are determined basing on the available aprior information. Such correlations are called a composite vector. A composite vector is a vector composed of some components of input and output variables, in particular, it can be any set, for example x — ( u 2 , u 5 , u 7 , u 8 ) , x — ( u 3 , u 4 , u 7 , x 2 ) [8].
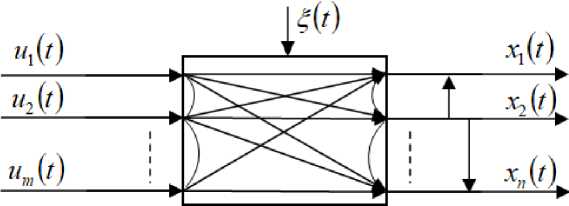
Fig. 1. The multidimensional system that implements the T -process
Рис. 1. Многомерная система, реализующая Т -процесс
The mathematical description of an object is represented as a system of implicit functions of the next form F j ( u ( t ) , x ( t ) ) = 0, j = 1, n . The identification problem is reduced to the problem of solving a system of nonlinear equations:
F j ( u ( t ) , x ( t ) ) = 0, j = 1, n (1)
relative to the vector components x , with known values of the input variables u .
Note that the type of equations F j ( ■ ) , j = 1, n remains unknown and cannot be interpreted as a model of the process under study. The task is to model such processes, i.e. T-processes.
Partially-parameterized multidimensional processes. Partially-parameterized multidimensional KT-processes differ from T-processes because their aprior information may correspond to a parametric type in some channels, and nonparametric in others.
A feature of identifying a multidimensional object is that the process under study is described by a system of implicit stochastic equations of the form:
F j ( u ( t ) , x ( t + т ) , ^ ( t ) ) = 0, j = 1, n , (2) where for some channels the functions F j ( ■ ) are not known, and for other channels they are known, т - a delay over various channels of a multidimensional system [3]. In the future, for reasons of simplicity, т will be omitted by shifting the values in the observation matrix by a value т .
In this case, the system of equations will take the form:
F ( u < j > , x < j > , a ) = 0, F 2 ( u < j > , x < j > , a ) = 0, _
« ... j = 1, n ,
F n —1 ( u < j > , x < j > ) = 0, F n ( u < j > , x < j > ) = 0.
where F j ( ■ ) are partially parameterized or unknown, a is the parameter vector.
Modeling of multidimensional inertia-free processes. Multidimensional KT-models combine T-models and K-models and represent a model in which there is a set of relationships between input and output variables, and they are known through some channels, for example, based on known laws of physics, and such dependencies are unknown through other channels. I. e., the presence of aprior information on various channels of a multidimensional object corresponds to both parametric and nonparametric types of source data. Therefore, we present the model system in the following form:
'F ( u < j > , x < j > , a ) = 0;
F ( u < j > , x < j > , a ) = 0;
« ... j = 1, n ,
F n _ , ( u < j > , x < j > , x s , u s ) = 0;
F , ( uj , x <J> , x s , u s ) = 0.
where xs , йs - the time vectors (the data set received by the s-th moment of time), and u < j > , x < j > - the composite vectors. However, even in this case, some functions F i ( ■ ) , j = 1, n remain unknown. Therefore, the problem of constructing KT-models is considered in conditions of nonparametric uncertainty, i.e. in conditions when the system (4) is known only through some channels and is not known to the accuracy of parameters through others.
The identification problem comes to the fact that for given values of the vector of input variables, it is necessary to solve system (4) with connection to the vector of output variables. For some channels of a multidimensional system, for which equations are known up to parameters, the coefficients are found, for example, by stochastic approximations or the least-squares method [9; 10]. For the other channels, where the equations with accuracy up to the parameter vector are unknown, the following two-step algorithmic chain [3] must be applied, which allows to find the predicted values of the vector of output variables from the known input ones. In the first step, the residuals are calculated using the following formula:
£ ij = F j ( u < j > , x < j > ( i ) , x s , г? s ) , j = 1, n , (5)
where F ( u < j > , x < j > ( i ) , x s , u s ) accepted in the form of a nonparametric estimate of the regression function Nada-raya-Watson [11]:
£J(i ) = Fj (u
= x j
( i ) -
s < m >
Z x j [ i ] П Ф i =1 k =1
' u k - U k [ i ] '
V csuk J
s < m >
Zn Ф
i =1 k =1
' u k - U k [ i ] '
V csuk J
Ф
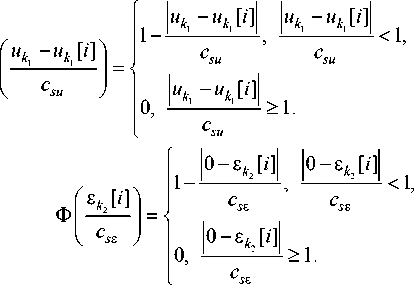
where j = 1, n , < m > - the dimension of the composite vector uk , then this notation is used for other variables. Moreover, the dimension of the composite vector may be different for different channels. Bell-shaped functions Ф ( ■ ) and the blur parameter c su k satisfy certain convergence conditions and have the following properties [12]:
Ф ( ■ ) <* ;lim s ^» c s = 0;
J Ф(c-k(uk-uk[i]))^u = 1;
П ( u )
lim s ^„ c - k Ф ( c - k ( u k - uk [ i ] ) ) = 8 ( u k - u k [ i ] ) ;
lims ^„ scs = *.
The second step is to evaluate the conditional mathematical expectation:
Xj = M {x | u
As a result the forecast for each component of the output variable vector will be as follows:
s < m >
Z j i ] ■ П Ф i =1 k 1 =1
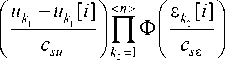
^
x j =
■ < m; f u - u , [ i ] ) < ” > f et [ i ] zn Ф I n Ф1-7- i =1 k 1 =1 V c su J k 2 =1 V c s £
j = 1, n, where the bell-shaped functions can be taken as a triangular core (11) and (12), and satisfy the conditions presented above.
The nonparametric algorithm (6), (10) is a two-step algorithmic chain that allows to find the predicted values of the components of the output vector for known components of input variables, in the case of stochastic dependence of output variables.
The relative standard deviation is taken as the error function:
Z ( x ' ( t ) - x j ( u < j > ( t ) ) ) 2
1 i =1___________________________________________ s2
у Z(xj(t)-Mx)
i =1
where x i ( t ) - observation on the object,
Xj ( u < j >( t ) ) -
forecast values of the object's output variables, Mx j – the average value for each component of the vector.
The problem of managing multidimensional discrete-continuous processes . Consider the scheme of a multi-dimensional object control system (fig. 2).
In fig. 2 the following notations are used: u (t) = (u1 (t),u2 (t),...,um (t)) - input controlled variables of the process; – input free, but controllable variables of the process; x(t) = (x1 (t),x2 (t),...,xn (t)) - output vari ables of the process; x * =( x1,..., xnj)eQ( x *)c Rn - setting action, ^(t) - random interferences affecting the process.
Control of T-objects is considered in conditions of nonparametric uncertainty, i. e. in conditions when the process model with accuracy up to the parameter vector is completely absent.
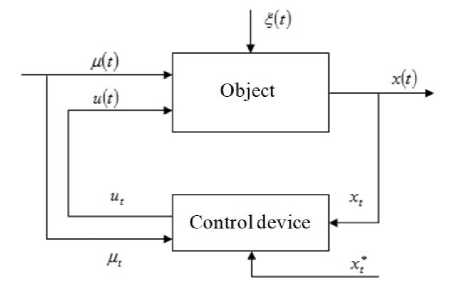
Fig. 2. Diagram of a nonparametric control system of an inertia-free object
Рис. 2. Схема непараметрической системы управления безынерционным объектом
In this case, the known techniques are not applicable and you should use other approaches to solve the problem.
In the problem of controlling a multidimensional process with stochastic dependence of output variables, the following multi-step algorithmic chain must be used: we take the input variable u * ( t ) arbitrarily from the area
Q ( u 1 ) . Any other input variable can be taken from the
specified area at any time. The next input variable u * ( t )
is found in accordance with the following algorithm:
s
Z u 2 Ф
i =1
< p >
*
u 2 =
u 1
c
*
u 1
< n >
П Ф
x
x
X
c
х П Ф
V=1
s
Z Ф
i =1
< P >
O v
Ц.
i "
' V
c
1V
u 1
c
u 1 i
< n >
П Ф
x
x
X
,
*
J j =1
c
х П Ф
O v
O v
V=1
c
V
where < n > , < p > - dimension of the corresponding composite vectors x and ц , < n > < n , < p > < p . Then we find the input variable u 3 ( t ) as follows:
s
Z u 3 Ф
i =1
< p >
*
u 3
u 1
u i "
cu 1
Ф
u 2
i " u 2
< n >
(
*
V
cu 2
П Ф
J j =1
x
x
X
cx
х П Ф
V=1
s
Z Ф
i =1
< p >
Ц v
u 1
х П Ф
V=1
c
ц V
A
1V
u 1
c u 1
Ц v
*
c
Ф
u 2
u l
< n >
, (15)
V
ц V
V
c u 2
П Ф
J
j =1
x
x
х
c xj
And then the control algorithm continues to find each
component of the object's input, and with each subsequent
step, the values of the input variables found in the previ-
ous step are added to the formula. The control algorithm
for a multidimensional system:
s
Z uk П Ф
uk
uk
< n >
i =1
c
П Ф
x
. *
x i j
X
< p >
*
c
* s
uk =
х П Ф
V=1
s k -1
Ц v
c
ц V
1V
ZП Ф
uk
uk
< n >
i =1 k =1
c
k
< p >
*
П Ф
x
*
c
xij
, k = 1, m . (16)
х
х П Ф
Ц v
ц V
A
V=1
c
V
In the control algorithm (16), the blurring parameters for input and output variables remain configurable c ,c and с , the following formulas can be used for uk xj ц them: cut = a uk - uk | + n , cxj =P|x *-xij + n and сц = y|hV_H3| + П , where a, P and у some parameters greater than 1, and the parameter 0 < n < 1 . Note that the selection of blur parameters cu, cx j and сц is performed at each control cycle. In this case, if cuk is defined first, then the definition c and с is carried out accord-xj ^V ing to this fact. The order in which the blurring parameters c ,c and с are defined is not important.
u k x j ^ V
Often in real process control tasks, the number of component vector u is greater than the number of component vector x . If the dimension of the vector u exceeds the dimension of the vector x , i. e. m > n , it is usually done as follows. To the number of component vector ц some (non-essential) components of the vector u are included, so that the dimension of the vector u and x to be equal.
Computational identification experiment. A multidimensional object with input variables u = ( u 1 , u 2, u 3 , u 4 ) and output variables x = ( x 1 , x 2, x 3 ) was used for the computational experiment. A training sample of input and output variables was formed for the object under consideration, based on a system of equations consisting of two parametric and one nonparametric channels. As a result, a training sample was obtained us , xs , where us , xs are the time vectors. In case we had a real object, the training sample would be obtained in the process of measurements performed by the available controls.
After receiving a sample of observations us , xs , you can start the task under study – finding the predicted values of output variables x based on known input variables u . The forecast for each component of the output variable vector is made according to the formula (10).
The configurable parameters are the blur parameters csu and cs E , which in this case are equal to 0.4 and 0.3, respectively (the values were determined as a result of numerous experiments to reduce the quadratic error between the output of the object and the model). Sample volume s = 1000, uniform interference that affects the components of the vector of output variables ^ = 0,07. Graphs for the outputs of the object x 1, x 2 and x 3 (fig. 3–5).
In fig. 3–5 “point” denotes the output value of the object, and “x” are values of the patterns found by the algorithm (5), (9). For clarity of the results in the figures, there are 20 sample points. The model describes the object fairly well with 7 % interference affecting the components of output variables.
Computational control experiment. The results of computational experiments for a multidimensional object with input variables u = ( u 1 , u 2, u 3, u 4 ) and output variables x = ( x 1 , x 2, x 3 ) using a multistep control algorithm
(13). For the object under consideration, the number of component vector u is greater than the number of component vector x . So replace u 4 ( t ) = ц ( t ) to make the dimension of the vector u equal to x . The input variable is free but controlled ц ( t ) e [0, 3] .
We underline that the researcher is not familiar with the type of system of equations that describes a controlled multidimensional object. Measurements of input and output variables are used as information about the object under study.
First, we present the results of the multistep control algorithm (16) with a variable step setting effect x * ( t ) (fig. 6).
As you can see from fig. 6, the output of the object x 1 ( t ) is quite close to the setting effect x * ( t ) . Here are the results of the algorithm with a soft changing setting effect x 2 ( t ) (fig. 7).
Here are the results of the algorithm when the task x * ( t ) is random (fig. 8).
Fig. 8 shows that the output of the object x 3 ( t ) is also quite close to the setting effect x * ( t ) . None of the known regulators can cope with such a task when the setting effect is random [14].
Still, this case is interesting from a theoretical point of view.
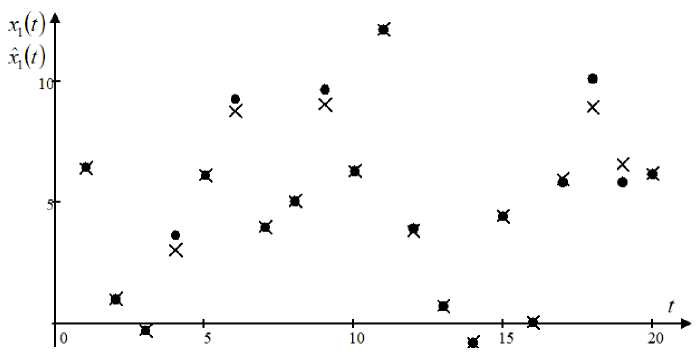
Fig. 3. The predicted values of the output variable x 1 with an interference of 7 %
Рис. 3. Прогнозные значения выходной переменной x 1 при помехе 7 %
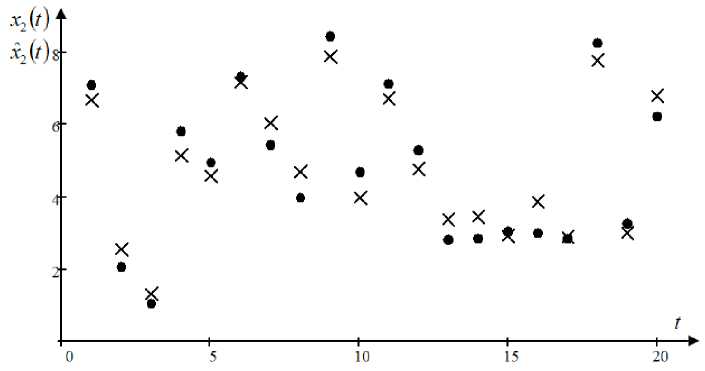
Fig. 4. The predicted values of the output variable x 2 with an interference of 7 %
Рис. 4. Прогнозные значения выходной переменной x 2 при помехе 7 %
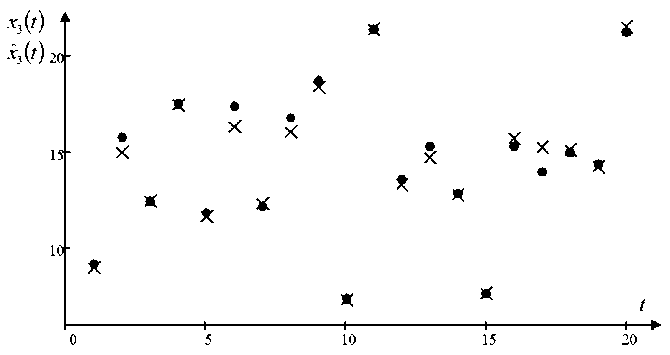
Fig. 5. The predicted values of the output variable x 3 with an interference of 7 %
Рис. 5. Прогнозные значения выходной переменной x 3 при помехе 7 %
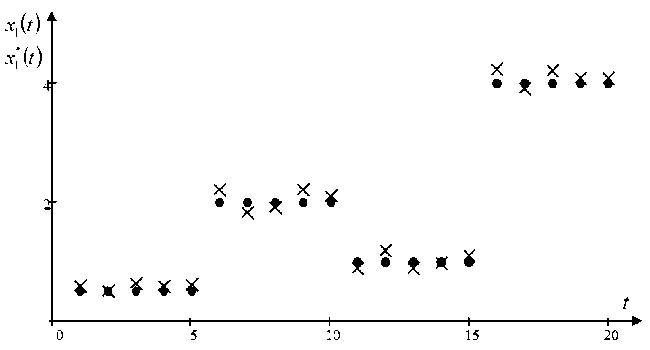
Fig. 6. Control under the setting action Л 1 ( t ) in the form of a step function
Рис. 6. Управление при задающем воздействии Л 1 ( t ) в виде ступенчатой функции
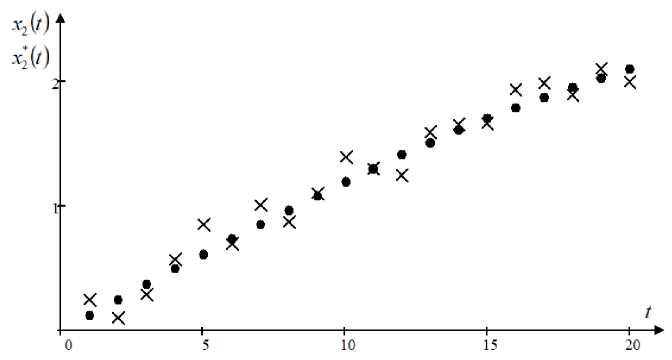
Fig. 7. Control under the set action л * ( t ) in the form of a soft changing function
Рис. 7. Управление при задающем воздействии л 2 ( t ) в виде плавно изменяющейся функции
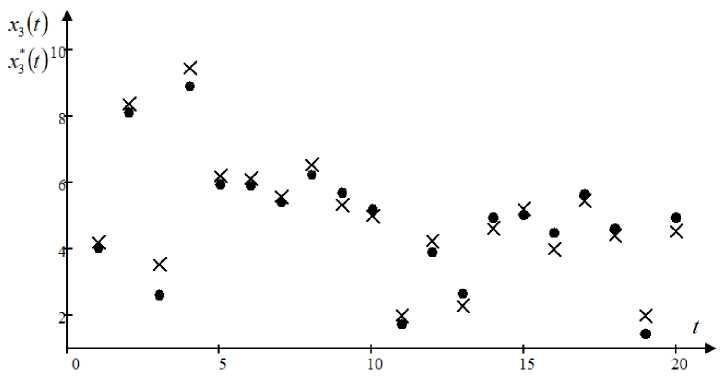
Fig. 8. The dependence of the output of the object x 3 ( t ) on the setting effect x 3 ( t ) , which is of random nature
Рис. 8. Зависимость выхода объекта x 3 ( t ) от задающего воздействия x 3 ( t ) , носящего случайный характер
Conclusion. In this paper, the problem of identification and control of multidimensional inertia-free systems with a delay in the conditions of a lack of aprior information considered. We note the fact that identification and control problems are considered under conditions of nonparametric uncertainty and, as a result, can not be presented with accuracy to a set of parameters. Well-configured modeling and control algorithms can be successfully applied in real control systems, diagnostics, decision-making, etc. [15].
These computational experiments on identification and control have shown satisfactory results of modeling multidimensional processes. At the same time, we investigated issues related to the introduction of various interference, different volumes of training samples, but also objects of different dimensions.
Список литературы Non-parametric multi-step algorithms for modeling and control of multi-dimensional inertia-free systems
- Sinyuta V. R., Yareshchenko D. I. [On nonparametric modeling of the process of catalytic hydrodeparaffinization]. Мaterialy XXII Mezhdunar. nauch. konf. “Reshetnevskie chteniya” [Materials XXII Intern. Scientific. Conf “Reshetnev reading”]. Krasnoyarsk, 2018, P. 160–162 (In Russ.).
- Yareshchenko D. I. [Some notes on the assessment of knowledge of university students]. Otkrytoe obrazovanie. 2017, No. 4, P. 66–72 (In Russ.).
- Medvedev A. V. Osnovy teorii neparametricheskikh sistem. Identifikatsiya, upravlenie, prinyatie resheniy [Fundamentals of the theory of nonparametric systems. Identification, management, decision making]. Krasnoyarsk, SibGU im. M. F. Reshetneva Publ., 2018, 732 p.
- Tereshina A. V., Yareshchenko D. I. [On nonparametric modeling of inertialess systems with delay]. Sibirskiy zhurnal nauki i tekhnologiy. 2018, Vol. 19, No. 1, P. 37–44 (In Russ.).
- Moiseev N. N. Matematika stavit eksperiment [Mathematics is an experiment]. Moscow, Nauka Publ., 1979, 224 p.
- Medvedev A. V. Neparametricheskie sistemy adaptacii [Nonparametric adaptation systems]. Novosibirsk, Nauka Publ., 1983. 174 p.
- Vasil'ev V. A., Dobrovidov A. V., Koshkin G. M. Neparametricheskoe ocenivanie funkcionalov ot raspredelenij stacionarnyh posledovatel'nostej [Nonparametric estimation of functionals of stationary sequences distributions]. Moscow, Nauka Publ., 2004, 508 p.
- Cypkin Ya. Z., Osnovy informacionnoj teorii identifikacii [Fundamentals of information theory of identification]. Moscow, Nauka Publ., 1984, 320 p.
- Zarubin, V. S. Matematicheskaya statistika [Mathematical statistics]. Moscow, MGTU im. Baumana Publ., 2008, 424 p.
- Linnik Yu. V. Metod naimen'shikh kvadratov i osnovy teorii obrabotki nablyudeniy [Least Squares Method and the Basics of Observation Processing Theory]. Moscow, FIZMATLIT Publ., 1958, 336 p.
- Nadaraya Eh. A. Neparametricheskoe ocenivanie plotnosti veroyatnostej i krivoj regressii [Nonparametric estimation of probability density and regression curve]. Tbilisi, Tbilisskiy universitet Publ., 1983, 194 p.
- Zhivoglyadov V. P., Medvedev A. V. Neparametricheskie algoritmy adaptatsii [Nonparametric adaptation algorithms]. Frunze, Ilim Publ., 1974, 135 p.
- EHjkhoff P. Osnovy identifikacii sistem upravleniya [Basics of identification of control systems]. Moscow, Mir Publ., 1975, 7 p.
- Fel'dbaum A.A. Elektricheskie sistemy avtomaticheskogo regulirovaniya [Electric automatic control systems]. Moscow, Gos. izd-vo oboronnoy promyshlennosti Publ., 1957, 808 p.
- Antomonov Yu. G., Harlamov V. I. Kibernetika i zhizn' [Cybernetics and life]. Moscow, Sov. Rossiya Publ., 1968, 327 p.


