Нормальная составляющая критической силы резания при подпорном и бесподпорном измельчении толстостебельных культур ножами дискового измельчителя

Введение. В настоящее время проблема нахождения критической силы резания при подпорном и бесподпорном измельчении толстостебельных культур в зависимости от конструктивных и кинематических параметров ротационно-дискового измельчителя изучена недостаточно. В данной статье сделана попытка приблизиться к решению вопроса о нахождении нормальной составляющей критической силы резания.

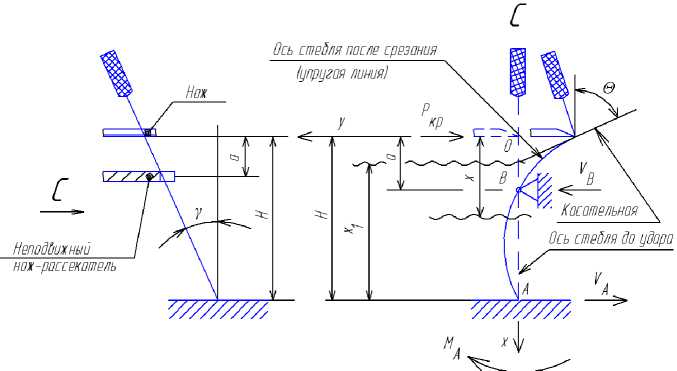
Нормальная составляющая критической силы резания стебля без учета защемления. Для проведения экспериментальных исследований по измельчению толстостебельных культур нами была сконструирована и изготовлена специальная экспериментальная установка, воспроизводящая работу измельчающего аппарата ротационно-дискового типа с применением трёх разных по форме сменных ножей в соответствии с рис. 1.

Из всех составляющих критической силы, действующей в зоне резания при подпорном измельчении, наибольшее значение имеет сопротивление резанию, нормальное к лезвию, составляющая которого определяется по формуле

NP p.₃ =5-A ^ -и р ,                                     (1)

где δ – толщина (острота) лезвия, м; ∆s – длина активной части лезвия, м; σ р – нормальные (контактные) разрушающие напряжения, возникающие в перерезаемом стебле, Н/м².

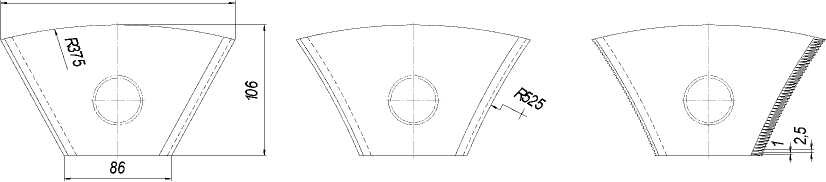
а)                                      б)                                        в)

Рис. 1. Экспериментальные ножи:

а – с прямым лезвием; б – с криволинейным лезвием; в – с насечкой

Исследованиями [1] установлено, что сила резания в среднем составляет 0,6Р кр (Р кр – критическое усилие резания). Следовательно, нормальная составляющая критической силы

δ⋅∆ s ⋅σ

N =         ^р =1,6⋅δ⋅∆ s ⋅σ .        (2)

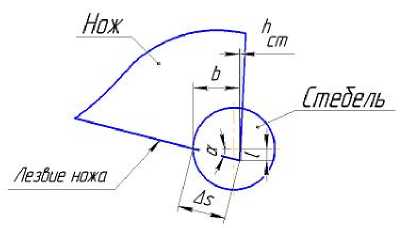
Рис. 2. Схема вхождения ножа с прямым лезвием в стебель

0,6                   ^р

Длину активной части прямого лезвия в соответствии с рис. 2 можно выразить через величину b, предполагая, что дуга l является прямым отрезком, так как значение h ст при данной конструкции ножей меньше 0,03 мм:

∆ s = ^b ,                  (3)

cos α где b – перемещение ножа в растительной массе в направлении подачи, мм; α – угол между кромкой лезвия ножа и направлением подачи стеб- лей при наиболее нагруженной позиции активной части лезвия, град. В свою очередь b можно выразить по формуле

60 s b =       ,

K⋅n и, как следствие, 1,(6)⋅δ⋅b⋅σ    60⋅1,6⋅δ⋅s⋅σ

N = ^{,             р} =      ^{,           р} ,                                     (5)

cosα         K⋅n⋅cosα где 60 – переводной коэффициент из секунд в минуты; s – подача, м/с; К – число ножей; n – число оборотов диска с ножами в минуту.

При криволинейном лезвии длина его активной части будет определяться как хорда радиусного участка ∆s. Величина радиусного участка ∆s в процессе резания будет постоянно изменяться в зависимости от варьирования подачи и числа оборотов.

Определим значение нормальной составляющей критической силы при резании ножом с насечкой криволинейного лезвия. Насечку лезвия можно рассмотреть как относительную зависимость от ненасечённого криволинейного лезвия, только нагрузка от срезаемого стебля будет располагаться не равномерно по лезвию, а иметь пиковый характер с наибольшими значениями на вершинах зубьев и наименьшими во впадинах между зубьями в соответствии с [1, с. 14] и эпюрой напряжений имитации работы зуба насечки в расчётном приложении Simulation проектной программы Solid Works Premium 2009.

Рассмотрим сплошную неравномерно распределённую нагрузку на участок лезвия с зубом от силы, приходящейся на зуб, в соответствии с рис. 3.

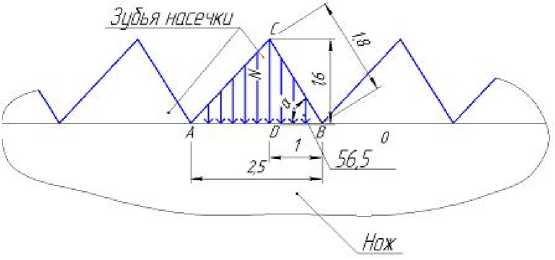
Рис. 3. Схема распределения нагрузки по основанию АВ зуба насечки

В схеме кривая АСВ является грузовой линией, а площадь треугольника АВС – грузовой площадью. Основание АВ зуба работает на нагрузку, распределённую по закону треугольника, так как наибольшее напряжение сосредоточено в точке С, а наименьшие напряжения – в контуре зуба во впадинах насечки. Наибольшая ордината расчётной нагрузки (высота СD треугольника)

N соответствует силе Nз = (где z – число зубьев на участке ∆s), так как в точке С стебель начи-z нает разделяться на части. Грузовая площадь, действующая на основание АВ, равна

• 1    • АВ • ВС • sin а . Величину АВ можно выразить через сторону CD, соответствующую N₃, то есть

  АВ = 2,5 = 1,5625·1,6 = 1,5625СD = 1,5625N з . Подставив данное отношение в формулу грузовой

площади, получим выражение

11,5625 N • 1,8• sin56,5 ° = 1,17 N .

2 ^з

Таким образом, при определении нормальной составляющей критической силы от ножа с насечкой длина активной части лезвия определяется аналогично криволинейному лезвию, а сама формула для ножа предложенной конструкции примет вид

1,(6) •§• b •„   60 • 1,(6) • 1,17 •§• 5 •а„

N = 1,17 • N₃ • z =              ^р- =                       ^- .                       (6)

cos а             K • n • cos а

Проведённый нами анализ печатных изданий выявил отсутствие изучения влияния на процесс энергоёмкости наличия или отсутствия контрножа (комплексного влияния параметров лезвия ножа, геометрических и механических свойств стеблей на энергоёмкость при подпорном и бесподпорном резании).

Нормальная составляющая критической силы резания стебля, защемленного в основании (бесподпорное резание). Приступая к определению опорных реакций стебля, возникающих при ударе стебля ножом, необходимо схематизировать опорные части, заменяя действительное растение приближающейся к ней схемой.

На схеме резания (рис. 4) свободно стоящий стебель без опоры под углом к вертикали Θ можно представить как консольную балку, защемлённую в основании и подвергающуюся действию силы Р кр на высоте резания Н от защемления.

Стрела прогиба в сечении ВВ 1 , мм [2, 3]:

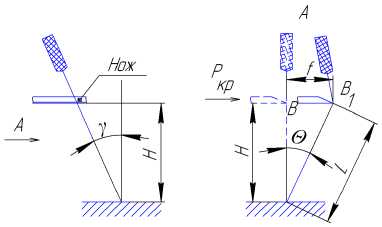
а)

Рис. 4. Схема стрелы

б) прогиба свободно стоящего стебля без опоры от воздействия критической силы: а – стебель наклонён навстречу направлению подачи измельчителя; б – вид слева

PK- •

H

f =

cos у J

64 • P k- •

h Y

cos у

3 E • Ix

3 E •n d⁴   '

где Н – высота резания, м; γ – угол отклонения от вертикали по направлению подачи, град.; Е – модуль упругости стебля

при растяжении, Н/м²; I x – осевой момент инерции сечения стебля, м⁴; d – диаметр стебля, м. Откуда

_n   0,04688 • f • E •n d ⁴

Р = —--------------, к-         f h Y3

( cosyJ а нормальная составляющая этой силы

N =

0,04688• f • E •n- d ⁴ • cosф

3 h Y cos y J

,

где φ – угол скользящего резания, град.

Стрела прогиба стебля вычисляется по формуле [4] f = V L - H² .

Так как силы в выражениях (5) и (9) теоретически одинаковы, то для прямого и криволинейного лезвия N можно выразить как:

60 -1,(6) -8- s -ст _р • Н ³ + 0,04688 f - E -п- d ⁴ - cos ф- cos³ y- K - n - cos a 2 К - n - cos a- Н ³

508- s -ст _р - Н ³ + 0,02344 f - E -п- d ⁴ - cos ф- cos³ у- K - n - cos a К - n - cos a- Н ³

Для лезвия с насечкой:

N =

.

60 - 1,(6) - 1,17 -8- s -ст _р • Н ³ + 0,04688 f - E -п- d ⁴ - cos ф- cos³ у - K - n - cos a

58,5 5- s -ст _р

2 К - n - cos a - Н ³

- Н ³ + 0,02344 f - E -п- d ⁴ - cos ф- cos³ y- K - n - cos a К - n - cos a - Н ³

.

Если разрешающей способности измерительного инструмента для определения отличия

величины стерни L от высоты среза Н на определённом этапе будет недостаточно, а это произойдёт, если прогиб стебля по сравнению с высотой резания будет очень мал (с углом поворота в плоскости среза меньше 0,5°), то расчёт критической силы будем производить через угол поворота сечения. Критическим условием будем считать пограничное определение, изложенное в работе [5], при котором разрушение пролёта (в нашем случае стебля) начнётся при превышении прогиба

• ¹    доли пролёта, то есть при f = H/1000. Для углов поворота сечения не больше 1° принято

считать [5], что тангенс угла равен углу, выраженному в радианах. Отсюда следует, что разрушение может произойти при

0 = tg 0 = -f = ——— = 0,001 рад , dH dH -1000

где Θ – угол поворота стебля в плоскости среза.

Угол поворота стебля в сечении ВВ 1 в соответствии с рис. 4 [6]: 2

P • кр

0 =---

Н

I cos yj =    ³² PKP • Н²

2 EIx       п - d ⁴ - Е - cos ² у

.

Откуда соответственно: для прямого и криволинейного лезвия:

N =

60 - 32 -1,(6) -8- s -ст _р - Н ² +0- E -п- d ⁴ - cos ф- cos² у- K - n - cos a

32 К - n - cos a- Н²

;

32008 - s -ст р - Н ² + 0 - E - п - d ⁴ - cos ф - cos² у - K - n - cos a

32 К - n - cos a- Н²

для лезвия с насечкой:

60 - 32 -1,(6) -1,17 - 8- s -ст _р - Н ² + 0- E - п - d ⁴ - cos ф- cos² у - K - n - cos a

32 К - n - cos a- Н²

3743,985028- s -ст _р - Н ² +0- E -п- d ⁴ - cos ф- cos² y- K - n - cos a

Нормальная составляющая критической силы резания стебля с опорными реакциями в основании и контрноже (подпорное резание). Теперь рассмотрим процесс подпорного резания. На схеме резания в соответствии с рис. 5 стебель с одной опорой, расположенный под углом к вертикали γ, можно представить как стержень, защемлённый в основании, а также опирающийся на нож-рассекатель и подвергающийся действию силы Ркр на высоте резания Н от ниж- него защемления.

Найдём зависимость между критической силой Р кр и углом поворота Θ в плоскости среза.

От заданной силы в ноже-рассекателе (в точке В) появится реакция V B , а в заделке появятся реактивный изгибающий момент М А и реакция V А .

Уравнения статики:

–Р кр +V B –V A = 0,                                       (17)

–М А +V B (Н–а)–Р кр ·Н=0.                                  (18)

Загружаем систему раздельно, сначала силой V B , затем силой Р кр . Суммарный прогиб в точке В должен быть равен нулю (f В = 0).

Прогиб в точке В от силы V B :

fBV B

Vb ( H-а 1

^ cos y )

3 EI_x

а)

Рис. 5. Схема угла поворота стебля в плоскости среза от воздействия критической силы при подпорном резании: а – стебель наклонён навстречу направлению подачи измельчителя; б – вид слева

Определим прогиб в точке В от силы Р кр . Для сечения, которое отстоит от заделки на расстоянии х 1 [4]:

Ркр • Н • x 2

y ~~£   3 "ITT

6cos y- E • I_x

x ₁

H

H - ^a

Подставим x1 =-----, тогда cos y

_ Р_Кр • Н ( Н - a )² f     Н - а )

f^P =I 3I.

^кр      6 cos ⁵ y- E • I_x (    Н • cos Y)

Суммарный прогиб

Jb = fl$VB_B + fBP_w = 0,

откуда

Далее

VB fB =-

H — a Y cos у J   Ркр ' Н(Н — a)2

3 EI_x

—

6 cos ⁵ у- E • Ix

V = Ркр (2 H + а ) B   2( H — а )

.

^{3 Р}кр ’ а

V, =------- и М. =

AА

3 — ^{H a} | = o, H •cos у )

Р • a кр

.

2 cos у

Начало координат помещаем на верхнем конце стебля в точке О. Для вычисления угла поворота Θ 0 воспользуемся универсальным уравнением по методу начальных параметров [5–7] и граничным условием заделки А: при х = Н y^/(H) = Θ A = 0:

EIx • 0 = EIx -0 0

H H Y Г H H Y VB ( H — a )²   PH ²

---- V ,--- П----

I A I                                            I                                                                          ^.

cos у cos у )    ^ cos у cos у )    2cos у 2cos у

EIx -0 o +

VB ( H — a )² 2 cos² у

P Н ² кр

2 cos2 у

= 0.

после чего получим уравнение

PH ²    P „(2 H + a )( H — a )²

EIx • 0 0 = -25_---кр—------^A

2 cos² у     4( H — a )cos² у

Р • a или, вынося за скобки ^кр , 2

4 cos у

EIx H

P • a

' 0 =         ( H + a ).

4cos2 у

Отсюда после деления обеих частей уравнения на жёсткость ЕI x окончательно находим n P 'а (и     ¹⁶ P "^{a (} Н ⁺ а )

0₀ =----"---( H + a ) =---- —2----,

4EIx • cos2 у           E • n • d4 • cos2 у или

E ’П’ d ⁴ ’0₀ • cos² у 16 a ( H + a )

Нормальная составляющая этой силы имеет вид

E ’П’ d ⁴ ’0₀ • cosф’cos²у 16 a ( H + a )

Так как силы в выражениях (5) и (27) теоретически одинаковы, то при подпорном резании для прямого и криволинейного лезвия N можно выразить как:

60 ’ 16 ’ 1,(6) ’S’ s ’Ст _р • a ( H + a ) + 0’ E ’П’ d ⁴ • cos ф’ cos² у’ K • n • cos a

16 К • n • cos a’ a ( H + a )

1600 5’ s ’Ст _р • a ( H + a ) + 0’ E ’П’ d ⁴ • cos ф’ cos² у’ K • n • cos a 16 К • n • cos a • a ( H + a )

.

Для лезвия с насечкой:

60 ’ 16 * 1,(6) * 1,17 ’5’ s ’Ст _р • a ( H + a ) + 0* E •n^ d ⁴ • cos ф^ cos² у* K • n • cos a

16 К • n • cos a • a ( H + a )

2720 5’ s ’Ст _р • a ( H + a ) + 0’ E •П’ d ⁴ • cos ф’ cos² у’ K • n • cos a 16 К • n • cos a • a ( H + a )

.

Заключение. В статье представлены развёрнутые формулы определения нормальной составляющей критической силы резания в зависимости не только от принципа среза, но и от основных параметров конструкции измельчителя и режимов измельчения. Опытные данные (значения мощности), полученные при испытании ножей на экспериментальной установке, хорошо согласуются с результатами теоретических вычислений по формулам, в которых основной составляющей являлась нормальная составляющая критической силы, действующей в зоне резания.