Нормативы потребности запасных частей для построения ресурсной модели

Социальная напряженность, связанная с качеством обслуживания пассажиров в больших городах Красноярского края, как правило, вызвана значительным количеством автобусов, находящихся в технически неисправном состоянии.

Это положение требует разработки новых методических подходов к определению затрат на запасные части (ЗЧ) для больших групп автомобилей при планировании нормативной потребности. Нижеприведенная методика оценки затрат автопредприятия базируется на нормативных методах, которые имеют ряд известных недостатков и не в полной мере учитывают затраты в себестоимости перевозок. Проведены исследования динамики затрат по фактическим данным и нормативным показателям, а также проанализированы особенности их статистического распределения. Статистические данные исследованы по средним расходам на запасные части по направлениям Красноярского края, а также по среднему годовому пробегу. Обработана выборка данных по 26 предприятиям, которые охватывают основные районы эксплуатации автобусного парка.

Предприятия сгруппированы и условно распределены по 5 направлениям, поскольку между этими группами есть различия в затратах ввиду возрастных характеристик, технического состояния, климатических, дорожных и других условий. Получены средние фактические затраты на ЗЧ одного автобуса по каждому автопредприятию. Средние величины по группам довольно близки друг к другу:

36,94

^Х красн ^— 39,24 Х ачинское — 31,74 X минусинское — X енисейское — 28,18Х канское — 21,75.

Обработка полученной выборки выполняется с использованием формулы Старджеса [1,2]. Длина интервала для группировки значений равна:

h    ^Xmax ^xmin

~ 1+3,322dgri где хтах - максимальное значение, хтаж=94,3;

x_min - минимальное значение выборки, x_min = 3,48.

В нашем случае объем выборки n = 26. Число интервалов при объеме выборки n = 26 получается равным 6. Длина интервала составляет:

_  94,3 - 3,48  _ h = 1 + 3,322 -1д26 = 15,14.

Для снижения погрешности при вычислениях примем число интервалов равным 10. В этом случае длина интервала составляет h = 9,08 и в некоторых интервалах есть пустоты. Эти пустоты не позволят определить функцию распределения. Для устранения пустот экспериментальным путем подбираем число интервалов, равных 5. При числе интервалов 5 длина интервала будет составлять h = 18,16.

Левый конец первого интервала примем 0, тогда левый конец второго интервала 18,16, второй интервал – 18,16; 36,32 и т.д. Для дальнейших расчетов производится подсчет частот попаданий элементов выборки в интервалы [х , , Х £ ₊₁) , где х , ₊₁ — х , + h. Для каждого интервала находятся относительные частоты и результаты заносятся в табл. 1.

Относительные частоты для каждого интервала

Таблица 1

Интервал	Относительные частоты п1/ /п	Плотность распределения w^ — п h
0; 18,16	0,423	0,61
18,16; 36,32	0,308	0,44
36,32; 54,48	0,115	0,17

54,48; 72,64	0,077	0,11
72,64; 90,8	0,038	0,06
90,8; 108,96	0,038	0,06

Находим для каждого интервала середину интервалов:

	Х 1 + Х i+1                                              (2)
Подставив значения, получаем:	0 + 18,16 2      = 9,08.

Для каждого интервала получены расчетные значения (табл. 2).

Таблица 2

Середина интервалов	Частоты ni	Относительные частоты Щ/п	Плотность распределения w^ = n4h.
9,08	11	0,423	0,61
27,24	8	0,308	0,44
45,4	3	0,115	0,17
63,56	2	0,077	0,11
81,72	1	0,038	0,06
99,88	1	0,038	0,06

Гистограмма плотности распределения частот (рис.1) строится согласно данным табл. 2.

Расчетные значения

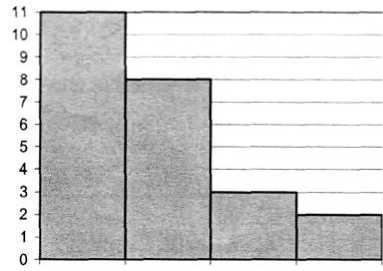
9,08      27,24      45,4      63,56

Рис. 1. Плотность распределения частот

Средняя величина затрат определяется как

Хсред = ^Si=i ni ' xi, где N — объем выборки (26); nt - относительная частота; xt - середина интервала.

Подставляя значения из табл. 2, получаем:

Х _сред = -6 (9,08 • 11 + 27,24 • 8 + ... + 99,88 • 1) = 29,34 .

Вычисление выборочной дисперсии выполняется по формуле:

£ в = J¹^^ Х i ^- Х сред ) • ⁿ t .

Подставляем значения в формулу (4):

D в = — ((9,08 - 29,34) 2 • 11 - (27,24 - 30,73) 2 • 8 + ••• 26

... + (99,88 - 30,73) 2 • 1) =367,87.

Выборочное среднее квадратичное отклонение (σ) вычисляется по формуле:

Получаем:

о = jD e .

о = V367,87 = 19,18 .

Далее вычисляется исправленная выборочная дисперсия:

„ 2   ^^i=1xi n'xсред) S =                      I n-1

Подставив значения, получаем:

₉   ((9,08 2 + 27,24 2 + ••• + 99,88 2 ) - 26 • 29,34 2 )

S2 =   ---------------2^---------------= 615,43.

Исправленное среднеквадратическое отклонение вычисляется по формуле:

S = VS 2 .

Подставив значения, получаем:

S = ^61543 = 24,81 .

Далее необходимо проверить гипотезу о экспоненциальном распределении. Функция распределения:

F(%) = 1 -e^-^*.                                (8)

Критерием оценки является критерий / 2 (хи квадрат), который вычисляется по формуле:

2         ■'

^{Z     L l} =1 Р-п

Вероятность попадания случайной величины X в интервал [Xi;Xi+l) вычисляется по формуле:

P i (X) = F(X ;₊J -F(X i ).                             (10)

Параметр Л вычисляется по формуле:

² = М(Х)

.

Подставив значения, получаем:

1          _

2 = 29134 = 0,034 .

В табл. 3 приведены результаты расчета.

Результаты расчетов двух интервалов

Результаты расчета

Таблица 3

Интервал	F(Xt )	m+i )	р	Pt • п
0; 18,16	0	0,461543	0,461543	12,00012
18,16; 36,32	0,461543	0,710064	0,248521	6,461548
36,32; 54,48	0,710064	0,843882	0,133818	3,479266
54,48; 72,64	0,843882	0,915937	0,072055	1,873435
72,64; 90,80	0,915937	0,954736	0,038799	1,008764
90,80; 108,96	0,954736	0,975627	0,020891	0,543176
108,96; + ∞	0,975627	1	0,024373	0,633694
Итого			1	26

Для дальнейших расчетов объединяем последние два интервала и их частоты (табл. 4).

Таблица 4

Интервал	P i	P i	P i • п
0; 18,16	12,00012	11	0,083352
18,16; 36,32	6,461548	8	0,366296
36,32; 54,48	3,479266	3	0,066018
54,48; 72,64	1,873435	2	0,00855
72,64; 90,80	1,008764	2	7,61Е-05
90,80; + ∞	1,17687	1	0,026582
Итого	26	26	0,55

По таблице 4 получили, что / Набл = 0,55. Смотрим таблицу критических точек распределений /² , при у = 0,95 и k =6-1-1=4 х Крит = 9,488 .

Так как х Н 2 _абл < х К рит , то гипотезу о экспоненциальном распределении принимаем.

Далее необходимо найти интервальную оценку параметра а=М(Х) математического ожидания случайной величины (СВ)X. Для этого определяется доверительный интервал отношением:

х сред -8 <  ^a <  ^х сред + ⁸ ,                              ⁽¹²⁾

где 8 =    . Число tv, где у = 1 - a = 0,95, находим по таблице. В нашем случае tv = 2,06. Тогда yN          ?                                                                   ?

δ = 10,02.

Х _сре_д -8 = 29,34 - 10,02 = 19,31;

X _сред + 8 = 29,34 + 10,02 = 39,36.

Таким образом, 19,31 < а < 39,36 – искомый доверительный интервал.

Интервальная оценка параметра о = о( Х ) находится по формуле:

S • (1 — q) < о(Х) <  S • (1 + q) при q <1 ,

0 < о(Х) < S • (1 + q) при q >  1, где q=0,3 находится по таблице, a S = 24,81 по формуле (7). Подставив эти значения, получаем

24,81 • (1 — 0,3) < о < 24,81 • (1 + 0,3) .

17,37 < о < 32,25 - искомый доверительный интервал.

Найденная средняя фактическая величина затрат на 1 автобус по каждому направлению показана на графике (рис. 2), и определена средняя величина по краю, которая составляет 29,34.

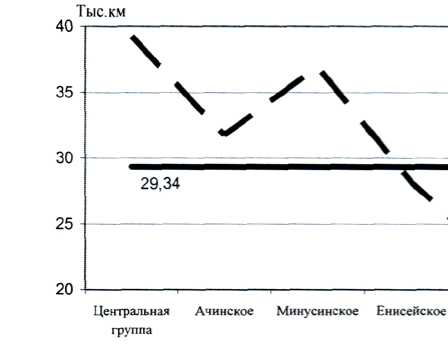
Рис. 2. График фактических средних расходов по направлениям

Аналогичные расчеты проведены по показателям годового пробега одного среднесписочного автобуса. Рассчитан общий пробег на 1 автобус в автопредприятиях соответствующих направлений и ниже на рис. 3 приведены данные плотности распределения частот, полученные путем аналитического расчета.

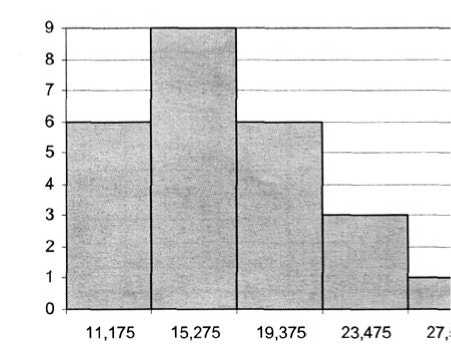
Рис. 3. Гистограмма плотности распределения частот

По результатам расчета построен график годового пробега на 1 автобус по каждому направлению (рис. 4) и его средняя величина по краю.

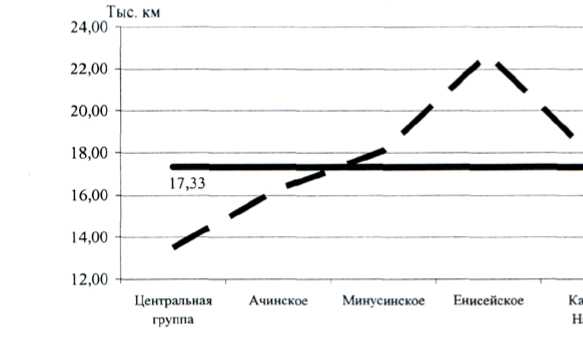
Рис. 4. График среднего годового пробега 1 автобуса

Для определения средних нормативных затрат на 1 автобус исследовались показатели по междугородним, пригородным и городским перевозкам по принятому объему выработки (n = 26).

нормативных затрат на ЗЧ по принятым направлениям со-

Рассчитанные средние величины ставляют:

^Х красн

= 28,88 X ачинск = 34,87 X минус = 38,66.

^ енисейск   48,59X канск = 43,50.

По формуле (1) находим длину интервала, где х_тах = 67,76, x_min = 23,92.

Подставляя значения, получаем h = 8,77.

Левый конец первого интервала примем x_min -^ 19,53, тогда правый конец первого интервала 28,30 (28,30; 37,07) и т.д. Для дальнейших расчетов производится подсчет частот попаданий элементов выборки в интервалы (x_i, x_i+1), где x_i+1 = x_i + h. Для каждого интервала находятся относительные частоты (табл. 5).

Таблица 5

Относительные частоты

Интервал	Относительные частоты ni/ /п	Плотность распределения W, = n4h
19,53; 28,30	0,231	0,026
28,30; 37,07	0,346	0,039
37,07; 45,8	0,231	0,026
45,84; 54,61	0,115	0,013
54,61; 63,38	0,038	0,004
53,38; 72,15	0,038	0,004

В таблице 6 приведены середины интервалов и их относительные частоты, по которым строится гистограмма плотности распределения относительных частот.

Середины интервалов

Таблица 6

Середины интервалов	Частоты ni	Относительные частоты ni/ In	Плотность распределения ^ i = n i /h
23,91	6	0,231	0,026
32,68	9	0,346	0,039
41,45	6	0,231	0,026
50,22	3	0,115	0,013
58,99	1	0,038	0,004

67,76

0,038

0,004

Плотность распределения частот изображается гистограммой на рис. 5.

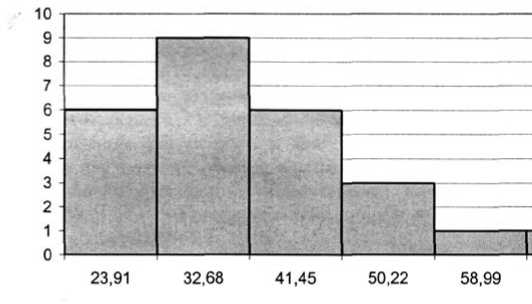
Рис. 5. Гистограмма плотности распределения относительных частот

По формулам (2)–(6) вычисляется выборочная средняя, выборочная дисперсия, среднеквадратическое отклонение. Результаты получены подстановкой данных:

Х _сред = 37,07 , D в = 69,52 , о = 8,34 , S² = 130,75 5 = 11,43.

По таблице критических точек распределений /² , при у = 0,95 и к =6 - 2 - 1=3 / К_рит = 7,815 .

Наблюдаемое значение составляет / н 2 а_бл = 2,55 .

Так как / Набл < / Крит , то гипотезу о нормальном распределении принимаем.

По формулам (12)–(13) найдем доверительный интервал для математического ожидания, среднеквадратическое отклонение СВ.

Для математического ожидания:

32,45< а < 41,68 – искомый доверительный интервал.

Интервальная оценка параметра о = о( Х ) .

8,00< а < 14,87 – искомый доверительный интервал.

Рассчитанные показатели средних нормативных затрат на 1 средний автобус по предприятиям определяемых направлений использованы при построении диаграммы на рис. 6.

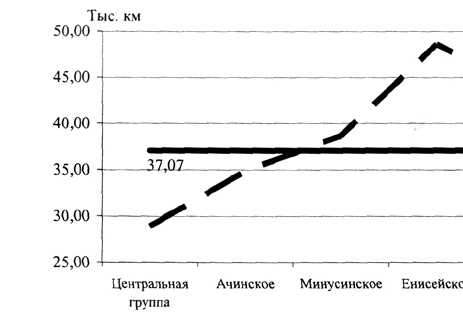
Рис. 6. График нормативных затрат на 1 автобус

При определении затрат на ЗЧ для каждого из основных направлений Красноярского края необходим логистический подход, использующий единую информационную базу данных по конкретным автобусным паркам соответствующих направлений. Учитывая реальное техническое состояние регионального парка [3], следует скорректировать расчетные данные определения затрат на запасные части в ранее разработанной методике [2]. Приняв утверждение некоторых авторов-практиков отечественного машиностроения [4], что затраты на запасные части изношенных автомобилей превышают стоимость нового автомобиля минимум в 2 раза, поэтому удваиваем ранее определенную норму по массе нетто. Статистические данные за последние 3 года по фактическим и нормативным показателям исследуемой выборки автомобилей подтверждают необходимость корректировки. В дальнейших расчетах норма расхода запасных частей на 1 приведенный автобус примем равной 240 кг, а цену 1 т массы можно принять 7 тыс. долл.

Нормативная потребность ЗЧ на 1 автобус вычисляем по формуле:

Р = Цг ПI, где P j – потребность в стоимостном выражении;

Ц I - цена единицы материальных ресурсов на 1 автомобиль;

П i - прогнозируемая потребность материальных ресурсов.

Согласно этому положению, обусловлено единство методического подхода при выделении необходимых средств по данной статье расходов в целях оперативности расчетов.

Климатические и географические условия эксплуатации на предприятиях енисейского и канского направлений влияют на расход ЗЧ, поэтому следует ввести поправочные коэффициенты. Значения коэффициентов (полученные экспертным путем и сопоставлением фактических и нормативных данных) соответственно составляют 1,3 и 1,2.

Анализ нормативных и расчетных данных расхода на ремонтный фонд на единицу автобусного парка по краю и его основным направлениям показал, что их средние значения довольно близки друг к другу (рис. 7).

Тыс. руб на I автобус 60,00 ? 50,00 40,00 30,00 20,00 10,00 0,00

Г Г Г I  ।

В   I   в _ I.   В

Центральная Ачинское Минусинсое Енисейское Каннское группа                                              Направление

• ■ Фактические затраты □ Нормативные затраты □ Расчетные данные |

Рис. 7. Гистограмма нормативных затрат на запасные части по основным направлениям региона

Подчеркнем, что значения фактических затрат по автопредприятиям не являются на один случайно выбранный автобус, а являются средними значениями по автопредприятию и именно распределение этих значений исследовалось.

Разница средних значений нормативных и расчетных показателей составляет около 3 %. Таким образом, предложенная методика расчета средних затрат на запасные части по предприятиям определенных направлений на единицу автобусного парка имеет реальную основу для применения.

Выполненные исследования являются этапом в решении комплексной задачи ресурсной обеспеченности автомобилей в рамках разработки проекта логистической системы материально-технического обеспечения технической эксплуатации автомобильного транспорта.