Нормированная корреляционная функция для анализа сигналов с разной частотой дискретизации

Постановка задачи

Корреляционный анализ применяется для широкого круга исследовательских и практических задач. Анализ взаимной корреляции между сигналами позволяет определять пространственное или временное смещение (задержку) между ними, может применяться для задач классификации, распознавания или для количественной оценки степени сходства между сигналами. Методики на основе корреляционного анализа позволяют достигать устойчивых практических результатов в радио- и эхолокации, информационных технологиях, медицинской диагностике, задачах локали- зации источника звука, задачах совмещения данных измерений и т.д.

Особый практический интерес представляет коэффициент корреляции Пирсона, который обладает свойствами инвариантности к усилению и математическому ожиданию сигналов, т.е. его применение позволяет оценивать сходство формы сигналов независимо от их постоянных составляющих и разницы в амплитудах.

В случае, когда возникает потребность оценить взаимную корреляцию сигналов, полученных с разной частотой дискретизации, стандартным приемом является передискретизация сигналов для приведения их к единой (как правило, меньшей) частоте дискретизации и последующее вычисление корреляционного коэффициента.

Задачей данной статьи является описание корреляционной функции, обладающей инвариантностью к разнице в усилениях и математических ожиданиях и позволяющей оценивать корреляционный коэффициент сигналов с разной частотой дискретизации непосредственно, без предварительной передискретизации. Кроме того, целью данной статьи является доказательство тождества между корреляционным коэффициентом и описываемой корреляционной функцией при равных частотах дискретизации для любых действительных сигналов.

Математическое обоснование

За основу корреляционной функции примем корреляционный коэффициент Пирсона

_ МУ-М^М^

^м Р |- ^ м2 Iм Wm ы1)

где х, У – анализируемые сигналы; ^м\} – оператор определения математического ожидания.

Примем, что .г и у – действительные дискретные периодические сигналы с периодом N отсчетов. Сигналы представлены в виде своих единственных реализаций, априорная информация об их функциях распределения отсутствует. Таким образом, справедливо выражение

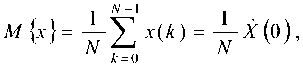
где хУ=^х(У '^N – спектр сигнала X , в нулевом аргументе является действительным числом для действительного сигнала X . Запишем корреляционный коэффициент с заменой математических ожиданий на средние значения и постоянные составляющие спектра

^x^y^v-x^yy также являются действительными. Примем также во внимание, что для действительных сигналов действительные компоненты спектров обладают четной симметрией, а мнимые нечетной (за центр симметрии можно принять половину частоты дискретизации). При этом произведение двух нечетных мнимых компонент спектров, очевидно, является также четной функцией. Итак, учтем, что сумма является действительной, выражение под знаком суммы имеет четную симметрию (особенности симметрии зависят от четности N), и вынесем слагаемое, соответствующее n = 0 , из-под знака суммы:

E x (A- )y(k ) = — ^ {Re (% (n Re (У (и ))+

+ Im У {n ))• Im (у (« ))}+

+ ^ ”^K -1^ Re (X (L^ J + 1 ))Re (У (L^ J + 1))+ + ^- (Re (^ (0 ))Re (У (O ))+ Im ^X (0 ))lm (у (0 ))), где /C = ^-l)/2. Если N четное, то присутствует предпоследнее слагаемое, а для нечетного N это слагаемое отсутствует, так как в этом случае ^-L^J=o. Введем функцию c(x,y) и учтем также, что (поскольку для нулевой гармоники мнимые компоненты равны нулю) А^(О)У(О)= Re(^(0))Re(y(0))+ Im(x(o))lm(y(o)) для любых действительных X и у , тогда

c(A',y)=^^^(A-)v(^)-2X(0)y(0) =

V^Kb Z X Z X

= ^ {Re У (n )) • Re (У (n )) +

+ Im У (/?))• Im (y («))} +

+ (C£z_L£JJ) R_e у (L^ J + 1 ))Re (у (L^ J + 1)) ■

Запишем корреляционный коэффициент в менее громоздком виде через функцию c^X,y\.

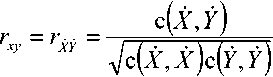
Таким образом, доказано, что корреляционный коэффициент дискретных действительных сигналов может быть рассчитан в спектральной области, то есть функция *XY ’ описываемая здесь, тождественна коэффициенту ’xy для действительных дискретных сигналов.

На практике удобно пользоваться формулой

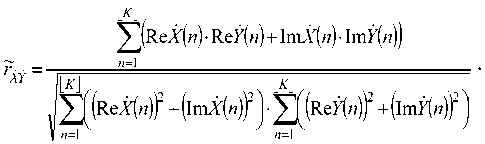
Функция ¹ at тождественна ^гхт ^{и Г}ху только для нечетных N , но при этом разница между ^rXY и F^y при больших четных N и сигналах с энергией, сосредоточенной в низкочастотной области, как правило, пренебрежительно мала. Кроме того, функция r^_Y обладает всеми свойствами корреляционного коэффициента, инвариантна к разнице в усилениях и математических ожиданиях сигналов и принимает значения из отрезка [–1; 1]. Расчет ^,-XY ^И * XY ведется в частотной области, что позволяет производить обработку сигналов в частотной области непосредственно в процессе корреляционного анализа для повышения его помехоустойчивости.

Анализ сигналов с разной частотой дискретизации

Рассмотрим ситуацию, при которой X И у имеют одинаковую форму, но разный масштаб по оси абсцисс, то есть разную частоту дискретизации (см. рис. 1).

Сигналы с разной частотой дискретизации без учета разницы

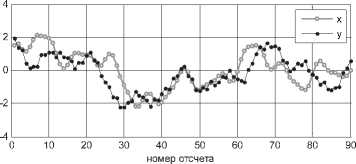
Рис. 1. Сигналы с разными масштабами

Используя информацию о разнице в частотах дискретизации (в данном примере разница 25%), выделим в сигнале с меньшей частотой дискретизации X участок сигнала, соответствующий сигналу у .

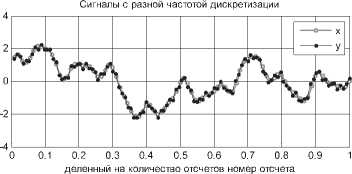
Рис. 2. Сигналы с разными масштабами, масштабированные по оси абсцисс

Таким образом, на рис. 2 число отсчетов век торов X и у приведены в соответствие с часто-

NT Fd..

тами дискретизации

Ny Fdy

Спектры исследуемых сигналов X и Y также имеют размеры ^x ^ ^у соответственно. Из формулы расчета спектра сигнала видно, что все гармоники спектра укладываются с целым числом периодов в отрезок длиной N, из чего следует, что сигналы на рис. 2 имеют совпадающие спектры от нулевой гармоники до половины наименьшей частоты дискретизации (см. рис. 3).

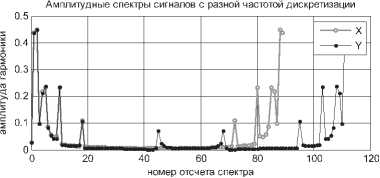
Рис. 3. Спектры сигналов с разными масштабами

Воспользуемся формулой ^XY , где величина K должна быть рассчитана по следующей формуле K = ^N_mm-\^2 , где ^min – длина наименьшего вектора из двух (в данном примере ^m=^-). Величина 'at для данной пары сигналов близка к единице (^,=0,9991), что является достоверным результатом, так как анализируемая пара сигналов получена из одного сигнала путем его передискретизации на разные частоты. Если в данном примере привести оба сигнала к наименьшей частоте дискретизации и рассчитать по полученным сигналам коэффициент корреляции Пирсона, то результат будет несколько хуже, чем при непосредственном анализе (/„= 0,9972).

Любая передискретизация, как правило, вносит в сигнал некоторую ошибку (см. рис. 4, где y приведен к шагу дискретизации сигнала), что связано с краевыми эффектами, явлением растекания спектра, несовершенством ФНЧ фильтров или погрешности интерполяции (в зависимости от способа передискретизации).

Сигналы, передискретизированные к одной частоте дискретизации

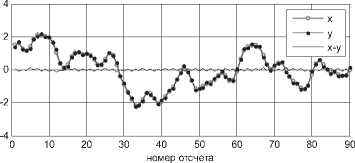
Рис. 4. Сигналы и ошибка передискретизации

Если проигнорировать разницу в частотах дискретизации и рассчитать коэффициент корреляции для рассматриваемой пары сигналов в том виде, как они изображены на рис. 1, то корреляция выражена очень слабо(rYV=0,66H).Важно отметить, что применение оконных функций в корреляционном анализе позволяет снизить погрешности, вызванные неточностями в определении частот дискретизации и локальными ухудшениями корреляционных признаков. Например, при значительной (порядка 25%) неучтенной разнице в частотах дискретизации (как на рис. 1) использование окон Хемминга для данной пары сигналов позволяет увеличить 7 ху с 0,6611 до 0,7769. Величина 1 лт при взвешенных .г и у с помощью окна Хемминга в данном примере увеличивается c 0,9991 до 0,9995 .

Оценим влияние разницы в частотах дискретизации на величины корреляционных функций с применением оконной функции Хемминга и без. Для данного эксперимента примем ^ =100, а частоту дискретизации y будем варьировать для достижения разницы в частотах дискретизации от 0% до 25% (Х„ варьируем в диапазоне 7V_y=1.257V_y).

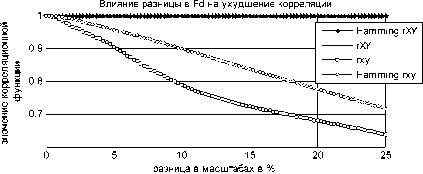
Рис. 5. Разница в масштабе и ухудшение корреляции

Следует учитывать, что характер спада XV с прямоугольным окном и с окном Хемминга (см. рис. 5) зависит от автокорреляционной функции и размера окна Nx ■> но при этом можно уверенно утверждать, что использование окна Хемминга (или другого окна со спадающими при отдалении от центра значениями) для расчета ^ ху значительно «смягчает» влияние разницы в частотах дискретизации. При этом значительного улучшения в параметре Г^у окно Хемминга не дает, однако в случае когда разница в масштабе будет зада- на для 'лт с погрешностью, преимущество окна Хемминга будет проявляться аналогично ситуации с ^ху • Графики рис. 5 также демонстрируют устойчивость функции ГХ¥ при работе с разными отношениями частот дискретизации. Аналогичные близкие к единице значения ГХУ получаются при отношении частот 200%, 300%, 400% и т.д.

Обобщение функции для многомерных сигналов

Обобщим формулу Г^ для случая многомерных действительных X и у одинакового размера. Перепишем c(Zr) для случая многомерных спектров X и Y. В таком случае N является век- тором и каждый i-ый элемент K рассчитывается отдельно (Ki =(W,-l)/2)

^c(^x’ ^r)=Z- •• Ei^Re№’---’^,7J)- ^Rwi ,...,«„,))+ Л]=() n_m=^                                        .

+ Im№„. ..,»,„))• 1т(у(и„.. .,«,„))}+

+£(k4^J)Re^^^

-Re(^(0,...,0))-Re(r(0,...,0)).

При подстановке обобщенного многомерного варианта ^с(Лу) в ^rX^’ получаем обобщенный многомерный корреляционный коэффициент, рассчитанный в частотной области. Многомерная функция ^rXY получается путем отбрасывания из ^c(x,y) слагаемых для гармоник с номером k-J+i и расчетом величины ^Ki как^=0v_min,.-l)/2.

Оригинальный сигнал 12x14

Сигнал 11x11 rXY=0.97761

Сигнал 18x15 rX/=0.96991

5        10        15

Рис. 6. Двумерная корреляция

Сигнал 10x14 rXY=-0.99433

2 4 6 8 10 12 14

Для демонстрации работоспособности многомерного обобщения ^ZAT синтезируем несколько двумерных (см. рис. 6) и трехмерных (см. рис. 7) градиентов. Для корреляционного анализа двумерных цветных изображений с сохранением информации по соотношению цветовых компонент можно выражение для двумерной ^с(Лу) заключить в сумму по отдельным цветовым компонентам.

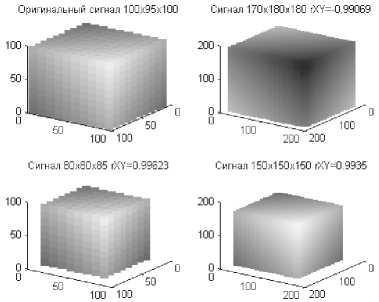
Рис. 7. Трехмерная корреляция

Выводы

Передискретизация сигналов к единой частоте дискретизации перед проведением взаимного корреляционного анализа вносит погрешность передискретизации. Применение корреляционной функции *Xt позволяет пропустить этот этап.

Функция г\т является корреляционным коэффициентом Пирсона, рассчитанным в частотной области и абсолютно ему тождественна для действительных сигналов. Обобщенная версия этой функции KXY применима для корреляционного анализа сигналов с разной частотой дискретизации, в том числе многомерных.

Тот факт, что расчет r^, ведется в частотной области, позволяет производить преобразования анализируемых сигналов в процессе расчета ^XY (линейная коррекция, фильтрация, применение окон PHAT или ML и т.д.).