Новая криптосистема на точках эллиптической кривой, основанная на проблеме упаковки рюкзака
Автор: Бабенко М.Г., Ляхов П.А., Червяков Н.И.
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 4 т.10, 2012 года.
Бесплатный доступ
В статье разрабатывается криптосистема на точках эллиптической кривой, основанная на задаче упаковки рюкзака. Для построения криптосистемы используется операция спаривания точек эллиптической кривой, заданной над конечным кольцом. Все арифметические операции выполняются в системе остаточных классов.
Криптосистема на точках эллиптической кривой, система остаточных классов, спаривание точек эллиптической кривой
Короткий адрес: https://sciup.org/140191587
IDR: 140191587 | УДК: 621.391
Текст научной статьи Новая криптосистема на точках эллиптической кривой, основанная на проблеме упаковки рюкзака
Современные информационные системы требуют особого подхода к сохранению секретной информации. Это обусловлено развитием технических возможностей потенциальных нарушителей, а также появлением новых алгоритмов криптографии и криптоанализа. Криптосистемы, основанные на использовании вычислительно сложной задачи упаковки рюкзака, обладают высокой скоростью шифрования информации, однако у них есть существенный недостаток. В большинстве случаев такие криптосистемы уязвимы для анализа с помощью алгоритма LLL, который аппроксимирует решение, являющееся кратчайшим вектором, содержащимся в решетке предполагаемых решений. Цель статьи – разработка криптосистемы упаковки рюкзака на точках эллиптической кривой над кольцом вычетов.
Для построения криптосистемы введем операцию спаривание на эллиптической кривой анало-гичнуюработе[1].Длялюбойточки PeE^CF^ выполняется следующие равенство (ni + iy = o, где о – точка в бесконечности. Обозначим за Е^ч) множество точек эллиптической кривой, которая задана уравнением v2 = x3 + ax + b , над расширенными полями GF^pk\ Для построения спаривания важно знать структуру группы точек эллиптической кривой. Ниже приведена теорема, описывающая структуру группы, когда эллиптическая кривая задана над полем GF^\ где Pi
– простое число, к > 1 и порядок группы точек эллиптичес ой кривой выражается формулой #E^GF^p^ = Р; ^\-t.
Теорема 1 [2]. Если P=p^p^p^ то группа циклическая. Если P=4PL то группа изоморфна ^^ pk — 1 (^ ^^p^ в случае t = z^ или изоморфна Z r- ®z в случае t = -^pi ■
Если / = 0, р, ^3(mod4), то группа циклическая. Если /-0, Pj = 3(mod4), то группа или циклическая, или изоморфна ^+1®^2-
Из теоремы 1 следует, что в случае, ког- да, r = 4р* иr – четное число, группа точек E^GF^ представляется в виде прямой сум- мы Z ®Z или Z ®z . Обоз-4Pl -1 4pi"v hi+x 4Fp\ начим эти группы ^ V^i 19 где /,-V^F-1 или i.=^+\.
Так как E ^/z j представляется в виде прямой суммы циклических групп, то можно зафиксировать некоторую образующую пару точек G; и H; таким образом, чтобы любую точку в ■^k] можно было представить с помощью них. Рассмотрим точки /’=a1,G,+Z>l,H,. и ^^i ^^, i ^^ i ~^" ^2, i ^^ i 9 принадлежавшие skL где ^.i^i.iKi^ e[0,/,-l]. Для некоторых зафиксированных целых аг,Де[0,/,-1] определим функцию следующим образом
^,,A ^k]x^k]^ La, ,Pi (Pi ’Q,) = (^Л, - a2.ib2,i Х«Ь, + PiHi) исключая тривиальный случай, когда «i и Pi одновременно равны нулю. Пусть Ga, C2 и G3 – три Абелевы группы. Билинейное спаривание является отображением e:GAxG2^G3 среди этих трех групп, и отображение должно удовлетворять свойству билинейности: для a,p eGx, у,д eG2, е(а + Д у) = е^а, у)+ е^Р, у), е(а,у + 5) = е(а,у)+е(а,5). Следующая теорема показывает, что функция ^«i,Pi задает билинейное спаривание. Теорема 2 [1]. Функция L«X обладает следующими свойствами. 1. Тождественность: 2. Билинейность: 3. Антисимметричность: 4. Невырожденность: для всех ИКМИ для всехр^л^А, Е^р, (^ + йЛА = Д„д кР,ЛУКР1 (QM и Д„А^Qi + Д) = Д„А (^й) + Д„А^ЛУ для любых Рцв^Е^], l^p^-l^AQ^- для всех 0^[',]. L^^.O^O, кроме того, если L^P’Q^0 для всех Й^М-тогдаP,=O. Lq p называется спариванием, поскольку оно отображает E[/,]x £[/,.] в £[/,] (аналогично традиционным спариваниям Вейля и Тейта). YP = Y mod р,, ZP = ZP mod p., XQiее XQ mod Pi, YQi ее Yg mod p;, Zg = Z0 modPj и z = 1 ..s Замечание. Значения XL, YL, zl представ- ляются в системе остаточных классов числами XLi,YLi, ZL по основаниям Pi • Приведем пример построения билинейного спаривания. Пример 1. Пусть задана эллиптическая кривая E(Fs ): y2 = x3 + 3x + 4 и Д, =F5 /(a2 +ar + l), тогда «df,J=27 имеет восемь торсионных точек третьего порядка: (-l,±(o'+ 3)), (2,±2), (a,+ct), (4tz + 4,±(a + l)). Билинейное спаривание можно задать с помощью следующих точек G = (2,2) и H = ^a,a\ 0G + 0H = 0; 1С + 0Я = (2,2); 2G + OH = (2,-2); 0G + 1H = (a,a) 1G + 1Я = (4 + 4tz,l + a) 2С + 1Я = (-1,-«-3) 0G + 2H = \G + 2H(-},a + 3); 2G + 2H = (4 + 4zz,4 + 4a), что изоморфно Z^ ^ z^. Из определения следует что e Процесс генерации ключей Пусть E , заданной уравнением в форме Вейерштрассе y3 = x3 + ax + b , над Zq, где a,beZq, q="Qpi, p, – различные простые числа и для всех i = !,...,» выполняется следую- щее условие: j < Pi < vv) и q> 1 . Числа Pi выбираются так, чтобы было большое простое число n в 160 бит или более в факторизации на простые числа порядка эллиптической кривой *Е\Е,У Далее, мы выбираем случайное число . Однако следующая супервозрастающая последовательность а/ = к-2 , выбирается так, чтобы удовлетворяла следующему ус- Рациональные точки OiP[i = 1,2,3,•■•,№') являются открытым публичным вектором рюкзака. Однако, как описано ниже, расшифровка эффективна, сообщаем каждому шифротексту и сумму r рациональных точек а;Р . Следовательно, количество ai равно ur. Здесь мы имеем ur > 100 , так что шифротексты могут иметь допуск достаточно грубой силы нападения. Затем рациональные точки avP, ... , uu,P, эллиптической кривой E(Fn), произвольная точка rY avP,...,atnPY EkFp\n^ и S = dR, где d^Zn случайно взятое публичное открытое. Затем для каждого Cj^i = l,...,zz), которое передается в качестве шифротекста, функция расшифровки задается следующим образом. Сначала вычисляется bu=e ь2, =Ы =^P,qY^ =^P,qY^ J , Ь^Л 44,2)4} =4ле)4У’ ь-А^ ’УлеГУ Процедура вычислений: сначала определяются bi\=bA,i 0" = 2,3,...,//), затем bU =Ь^з-Фп (z = 1,..., u,j = 2,3,..., 2' -1). В завершение мы находим многочлен как /У) = (л- - Ьл )• • ■ (% - Р2,._, \х -1) (/ = 1,...,и). Публичный ключ и секретный ключ задаются следующим образом. Публичный ключ: ахР,...,аигР,Е^,К,8,г Секретный ключ: d , /iM, е(Л5), а0, ..., аю., Q Алгоритм 1. Шифрования для криптосистемы упаковки рюкзака на эллиптической кривой Вход. Двоичный вектор М = ^тхлп2,...,ти(\ /77, е(0,1), (z = 1,2,...,///-), Публичный ключ oJ'.-.a.P.E^. R.S.r. Выход.Шифротекстс, с, схх, с]2,..., c,,,^ , У<-1,2 ■ 1. с = о 2. Для / = 1 до иг выполнять следующие действие: 2.1. С = С + т^РУ 3. Для / = О до и - 2 выполнять следующие действие: 3.1 с_=о. 3.2 . Для j = 1 до г выполнять следующие действия: См = С, + mr,+Yar.iP^- 4. Генерируются случайно числа tx,tn,...,tu_x. 5. Для i = 1 до // — 1 выполнять следующие действия: 5.1. CiV=t,R, 5.2. . 6. Вывод C, Cn, C12,...,C„_L1, CU_X2 Алгоритм 2. Дешифрование для криптосистемы упаковки рюкзака на эллиптической кривой. Вход. Шифротекст С, CH, C|2, ...,CM_u, ki-1,2 иd, fAxY e^P,Q\ a0,,ax,..., aur. Выход. Двоичный вектор M 1. Для i = 1 до // -1 выполнять следующие действия:с,=с^-ас1Л. 3. Для / = 1 до и -1 выполнять следующие действия: 3.1. x = e 3.2. y = y/x. 3.3. Для / = О до r -1 выполнять следующие действия: 4. Для j = 0 до r -1 выполнять следующие действия: 4.3.1.Е сли /^v/e^eh-^O, то 4.3.1.1 .^,„.-; =1 , 4.3.1.2 x = xle"”H , 5. Вывод M. иначе mlir-i = 0. Действие расшифровки Во-первых, объясним расшифровку C7] : пусть r = e(C1,5)/e(P,5k = = e^mx ka\p^+ ... + »/,.(a,.P\QYe^,.P,Q^ = €^(£11?) +... +m,. (p,P) -a,P,QA = = е^тАсц +... + mrar — ar ^P, Q) = = e(k(u71 +... + mr2'4 -2'~l^P,Q^ = ^(e(P,Qf'+-^^^ Если ml+... + mr2' *—2' *>0, мы называ- ем это положительное значение спариванием. В противном случае мы называем его отрицательным значением спаривания. В уравнении bv=^P,Q^ (v^l^^,...^-1) bXj все значения различны потому, что к • 2' <----< 77 , и значение спаривания определяется единственным образом. С вида 1,2,...,2' «супервозраста-ет», так как 1 + 2 + ... + 2' "2 <2' "1, следовательно, 2К — 1 — К — 1 , , _ 2 <2 . Если mr = 1, тогда 7 (У) = 0 , потому что спаривание имеет положительное значение, равное одному bM ■ В противном случае УУМ, потому что спаривание Y имеет отрицательное значение, не равное любому Ьм . Повторяя процесс, мы дешифруем С; от mr к mY. Аналогичным образом мы можем расшифровать C,. Пусть Y^C^QYe^QY' = = еЦ,-1)г+1 («(/-1 y+123)+... + mir ^airp\ Q)/e{airP, g) = = еЦм ),-+i ("(/-i),-+i ^)+• • • + mir ^irP^ - a,rP, Q) = -е(Ц;_1),.+!а(,-_1Н +- + 'Ч,-«л- -P, к’Й = е^Цм^У^1’^ ^..Am,2"-V -2"-1>,g) = 4(p,e)tHM2,'~" = ^ле)^,'ч1к(и),^---™РгЧ-2гЧ). Поскольку ^=^(леп J, то (7 = 1, 2,3,...,2'-1). Если mir =1 ’ то ZW=O, потому что Y является положительным значением спаривания и равно одному из Ьу . В противном случае *0, потому что Y есть отрицательное значение спаривания и не равно любому by ■ Повторяя этот процесс, дешифруем C; из mir c тИу+х. В итоге получим х,=е(с,ешс,,енс..„д))== e(C-C,-...-C._„g) = e(C,.Q), то есть мы расшифровываем C1( аналогичным образом с расшифровкой с, • Вычислительная сложность спаривания равна log 72. В шифровании вычислительная сложность сложения на эллиптической кривой тоже полиномиальная log p. В дешифровании сложность вычисления частного значения спаривания также имеет полиномиальное время, так как они вычисляются по mod p. Хотя мы судим о том, что значение спаривания положительно или отрицательно путем расшифровки функции, оно вычисляется за полиномиальное время, поскольку вычитание и умножение по mod p рассчитывается за константу. Исследования выполнены при поддержке гранта РФФИ 12-07-00482-а. Рюкзачная криптосистема на эллиптической кривой обладает следующими преимуществами относительно криптосистемы рюкзака над числами. Криптосистема не расшифровывается LLL-алгоритмом засчет использования эллиптической кривой. Шифротексты – это точки эллиптической кривой. Вычислительная сложность расшифровки – полиномиальное время с помощью функции расшифровки. Все арифметические операции с точками эллиптической кривой можно эффективно выполнять в системе остаточных классов с использованием приближенного метода [3]. 1. Lee H.-S. A self-pairing map and its applications to cryptography // Applied Mathematics and Computation. 151, 2004. – P. 671-678. 2. Болотов А.А., Гашков С.Б., Фролов А.Б., Часовских А.А. Элементарное введение в эллиптическую криптографию: Алгебраические и алгоритмические основы. М.: КомКнига, 2006. – 328 с. 3. Червяков Н.И., Бабенко М.Г., Ляхов П.А., Лавриненко И.Н. Приближенный метод ускоренного обнаружения и локализации неисправного вычислительного канала ЭВМ, функционирующей в системе остаточных классов // Нейрокомпьютеры: разработка, применение. №10, 2011. – С. 13-19. NEW CRYPTOSYSTEMS ON ELLIPTIC CURVE POINTS BASED ON THE PACKAGE KNAPSACKS DIFFICULTY Babenko M.G., Lyakhov P.A., Chervyakov N.I.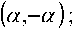
2. Y = 4C,qV
Список литературы Новая криптосистема на точках эллиптической кривой, основанная на проблеме упаковки рюкзака
- Lee H.-S. A self-pairing map and its applications to cryptography//Applied Mathematics and Computation. 151, 2004. -P. 671-678.
- Болотов А.А., Гашков С.Б., Фролов А.Б., Часовских А.А. Элементарное введение в эллиптическую криптографию: Алгебраические и алгоритмические основы. М.: КомКнига, 2006. -328 с.
- Червяков Н.И., Бабенко М.Г., Ляхов П.А., Лавриненко И.Н. Приближенный метод ускоренного обнаружения и локализации неисправного вычислительного канала ЭВМ, функционирующей в системе остаточных классов//Нейрокомпьютеры: разработка, применение. №10, 2011. -С. 13-19.


