Novel Approach to Solve Resource Constrained Project Scheduling Problem (RCPSP)

Published Online September 2016 in MECS

The Resource Constrained Project Scheduling Problem is a general name assigned to software development projects and which needs proper scheduling mechanism. To allocate resources in a software development environment, we have to consider many things like time, resources, cost and budget. The resource generally refers to as people, developers, skills, machines, tools, software, money, products and systems. The scheduling problem can be represented as set of activities or set of skills and resources spent in a simple way. The resources are analyzed, divided with respect to project size and budget. The skill set and developer allocation to a particular project needs to be carefully analyzed to complete the project on time.

In real time, which involves handling of multiple projects at the same time and one project should not get affected due to other project resource constrains. The resources will be hugely on demand while handling project simultaneously. The scheduling becomes an integral part of software development which needs more care and attention. A review about resource constrains scheduling problem is first given by Kelley. This project scheduling problem in resource constrain environment is considered as a NP hard problem. There are many optimization techniques to solve NP hard problem but most of them are complex and difficult to handle.

This paper gives solution to allocate resources efficient and schedule the project to complete the software development project within time. Here cost is not taken as the main entity but at the same case it focuses more on time and complexity. The resource constrained project scheduling algorithm is designed using genetic algorithm. The test cases are analyzed to provide flexibility and handle time complexity. This paper also aims to improve the iteration level to solve the problem of scheduling.

In software development field, deadline to complete the project will be given first priority. If a project is completed after the stipulated period of time, the client will not accept the project and its will be a huge loss to the software development team. The cost involved and the resources utilized will be of no use. So to avoid the problem of resource scheduling with minimal resource, this paper has given solution to allocate resources efficiently and complete the project within the stipulated time.

This paper is organized as follows, section II explains about background and related work, section III gives overall idea about problem description, section IV gives proposed solution of resource constrained problem, section V tell us how this paper validate and implement the solution and finally paper ends with section VI conclusion.

• II.    Background and Related Work

In the literature, there are several papers which tries to solve resource constrained project scheduling problem but not all proposed algorithms are can able to implement and solve the problem. This paper takes genetic algorithm to solve resource constrained project scheduling problem. There are some novel approaches and algorithms were studied to support this paper. The most of the previous work concentrate on scheduling the resources based on cost and it does not take time complexity of the project. Few parameters from the previously used algorithm were identified and taken into consideration to build a novel solution for resource constrained project scheduling problem. Some of the literature survey and background knowledge are explained in this section.

Chaleshtarti and Shadrokh [1] proposed branch and cut algorithm to solve resource-constrained project scheduling problem of non-renewable resources and renewable resources (RCPSP-NR). The algorithm structure is developed using many techniques and fathoming rules to minimize the solving process. The algorithm provides lower bounds for the problem in any middle stage of the solving process. The problem difficulty degree is based on some parameters such as number of activities, number of nonrenewable resources and number of procurement periods of nonrenewable resources. Some sample instance sets with different parameters are created and the experimental analysis is done by the proposed algorithm and also CPLEX solver to show the difficulty degree and the result is compared. The analyses result demonstrated that the performance of the Branch and cut algorithm is better for solving large instances compared to the performance of CPLEX solvers better in small instances [1].

Chaleshtarti and Shadrokh [2] have conducted a study using the same RCPSP-NR algorithm. In this work, study is focused on partially renewable resources as compared to completely non-renewable resources as a special case. The basic branch and four bound algorithms of RCPSP for RCPSP-NR are considered and these are the extension alternatives algorithm (EAA), precedence tree algorithm (PTA), minimal forbidden sets algorithm (MFSA) and minimal delaying alternative algorithm (MDAA). In addition, many customized method rules are introduced like bounding, dominance, branching and fathoming. Overall computational experience is done using previous four proposed algorithms. CPLEX solver is used in the comparisons and analyses. Different instances with various parameters are created. The analysis result displayed that some parameters has high relative effect in the algorithms and the CPLEX solver performance, specially numbers of procurement periods of nonrenewable resources, numbers of activities and numbers of nonrenewable resources. Each algorithm and the CPLEX solver had the best performance under different circumstances [2].

Karthikeyan et al. [3] worked in the key area of scheduling where they proposed a hybrid discrete firefly algorithm (HDFA) to solve the problem of complex scheduling which multi-objective job shop problem is considered and a number of resources in case are limited. The Main constraints of the scheduling problem are how to execute the operations sequentially and process them in which machine. The Study considered three key factors which are time maximization to complete job, workload across the critical system and across all the systems. The flexible job-shop scheduling problem (FJSP) structure is defined and the performance of the proposed algorithm is evaluated by Benchmark problems. Moreover, test computational results displayed that the HDFA is an efficient algorithm when considering the multi-objective or combinatorial scheduling problems because it reduced the computational time for scheduling the operations [3].

Zhangetal. [4] Introduced the hybrid of two algorithms, namely particle swarm optimization (PSO) and differential evolution (De) to try solving the problem of multimode resource constraint (MRCPSP). The algorithm uses two layers coding structure, where PSO is used for solving the scheduling problem in the upper level and DE is used for the project execution calculation in lower layer. The test function of project scheduling problem library (PSPLIB) is used to evaluate the effectiveness of the algorithm. The results demonstrated that the hybrid of PSO and DE algorithm is efficient for combinatorial problems [4].

As in [5], multi-mode resource availability cost problem (MMRACP) is solved by the model to reduce the cost of resource availability required to complete all activities at deadline of a project. The (MMRACP) is NP-hard problem which indicates that direct solution or exact one is nearly impossible; therefore, we need a model which can solve it. A heuristic based algorithm is proposed to improve the fitness of the solution. The model also assumes that deadline if fixed and the issue is revolving around cost. The algorithm is complex compared to RACP and test results displayed that Modified PSO increases the work efficiency, but overall provides the results which are comparatively better as it is based on heuristics [5].

Dalfard and Ranjbar [6] proposed a hybrid genetic algorithm to solve the multi-project scheduling problem specially assembly flow-shop scheduling problem with sequence-dependent setup and transportation times. The algorithm is the combinations of RCMPSP and simulated annealing which are based on heuristic and meta heuristic methods. The main objectives are, minimizing of weighted, make span, the sum of total weighted squared, total weighted squared earliness and finally, number of tardy jobs. The Lingo 8.0 software is used to evaluate the proposed algorithm. The test results yield showed that the working of this approach is better as compared to multipurpose rules of time scheduling because of prioritization factors [6].

Wulianget al. [7] proposed a model that uses a Bi-level of the Genetic Algorithm (GA) for solving the multimode critical chain project scheduling problem. The upper level contains the GA for execution measurement for activities and lower level handles the scheduling. The model focused on lower the project duration time in critical chain, calculation of project buffer and prioritization and calculation of non-critical chain operations. The algorithm was tested using instances of PSPLIB and showed the improvements over the previous approaches [7].

Lorterapong and Ussavadilokrit [8] worked on Construction scheduling approach for constraint satisfaction problem (CSP). The CSP is developed to provide a framework for systematic constraint modelling and effective schedule generation. The rationale of this research work is to provide a better approach as compared to CPM-based methods so that the drawbacks of these approaches can be eliminated. The new scheduling methods use the modifications in existing CSP approach as CSP itself portraits the best orientation of scheduling. The new methods use the human-machine in coordination to generate the schedule [8].

C.Chai [9] worked on modeling a new approach where the resource constraint projects scheduling problem can be resolved in better way using GA. The problem domain is NP-hard which indicates no exact solution and increased complexities therefore, traditional approach for calculating the solution is meaningless. The major focus is scheduling for resource-constrained projects. The paper further devised the mathematical model for representation of conceptual model using GA. The problem modelling assumes that a number of activities are definite, non-pre-emptive mode is applicable, resources need it determined. The overall goal is achieved the shortest possible execution time based on GA so that a time-cost can be reduced to its best. A practical problem is in case when project development required working faster and Research and development products are to be introduced in the market as soon as possible [9].

Jorge et al. [11], worked on project scheduling for Software development systems. The introduction of SDLC model is used to specifically focus on the software projects scheduling problem. The algorithm focused towards Software Development Library (PSPSWDLIB). The results showed that same approach can be adapted by any scheduling problem, but based on three factors scope, time and cost, the software project scheduling will somehow differ from others. The reasons of the specific scheduling primitives for covering SDLC are important [11].

Peixoto et al. [13] discussed the Staffing and scheduling problem in Software Development projects. The adoption and non-adoption of industrial settings are argued for finding the optimized solutions. The size and type of the project affect the delivery times. Therefore, in order to get better results and practice the finding solution for appropriate projects, the involvement of stakeholder is very important [13].

Peng and Huang [14] worked on resource constrained scheduling problem where the specific part of study was pre-emptive bound. A new approach of destructive lower bound for NP-hard problem is proposed. The approach is tested by performing the computations on whopping 2,040 benchmark instances of PSPLIB. The results gathered from these tests showed that the approach is more adaptive and provides the excellent scheduling results while outperforming many other algorithms. Performance improvement is reported using the 5 best lower bounds of instances [14].

Table 1. Limitations of Literature Review Papers

Paper Title	Limitation
A Branch and Cut Algorithm for Resource-Constrained Project Scheduling Problem Subject to Nonrenewable Resources with PreScheduled Procurement [1]	The comparison study was done with CPLEX solver. While there are other algorithms for constrained resource problem, which are not taken into account for performance results.
Branch and Bound Algorithms for Resource Constrained Project Scheduling Problem Subject to Nonrenewable Resources with Prescheduled Procurement [2]	The study of partially renewable resources, is done in an ambiguous way. As both CPLEX and new method show results falling in similar margins.
A hybrid discrete firefly algorithm for multi-objective flexible job shop scheduling problem with limited resource constraints [3]	The comparison made with other methods show the effectiveness of algorithm, but the real-world demonstration of results is not included.
Hybrid Particle Swarm and Differential Evolution Algorithm for Solving Multimode Resource-Constrained Project Scheduling Problem [4]	The study focused on specific types of instances of PSLIB.
Solving the Multi-Mode Resource Availability Cost Problem in Project Scheduling Based on Modified Particle Swarm Optimization [5]	The NP-hard problem solution is presented and modelled by the further work is yet to be done to demonstrate the more realistic results.
Multi-Projects Scheduling with Resource Constraints & Priority Rules by The Use of Simulated Annealing Algorithm [6]	Results in current testing showed advantage but the model is not fully mature, as other goals for costing factor are not addressed yet.
A Genetic Algorithm for Solving Multi-Mode Critical Chain Project Scheduling Problem [7]	Model is based upon the existing CPM model and doesn’t cover other costing measurement aspects other than time minimization.
Construction Scheduling Using the Constraint Satisfaction Problem Method [8]	The existing CSP method is only modified and a new way of calculation is used, while the idea remains same.
Modeling Resource-constrained Project Scheduling Problem and its Solution by Genetic Algorithm [9]	Genetics algorithm is the basic one and similar research work is already present in area.
An improved particle swarm optimization for the resource-constrained project scheduling problem [10]	Resource constrained scheduling implemented shows improved work. But still needs work done to make it mature enough.
Project Scheduling Problem for Software Development Library – PSPSWDLIB [11]	Paper does not cover all aspects of scheduling in SDLC.
Research    on    Project Scheduling Problem with Resource Constraint [12]	Work is more theoretical and argumentative.

Haouari et al. [15] studied critical chain scheduling method. The method uses a differential evolution algorithm as a framework to cover the results from two points. The performance of the algorithm was tested against the ILOG CPLEX and priority rules. The effectiveness of algorithm, to find the optimal solution, was tested on dataset of PSPLIB. The results displayed improvements when a single mutation strategy was used [15].

All the above mentioned approaches have some limitations in their teaching methods. These limitations are displayed in Table1.

• III.    Problem Definition

Software projects differ from other project like manufacturing, construction and building on many parameters. The most crucial factors are inclusion of skill-intensive tasks, task and skill mapping, availability human resources with required skills, skill-dependent cost and fluctuation in task completion durations due to skillintensive nature of its tasks. So, in a software project scheduling must be done with a multi-objective approach. In solving the classical problem of resource critical project scheduling problem in software projects we propose to apply the Genetic Algorithm due to its dependable scalability features with the heuristics method as demonstrated in the paper by [9]. The heuristics function to evaluate the fitness of the objective function will be a function dependent on the parameters required to complete a Software development project.

• A.    Description of Terms, Parameters, Assumptions and Functions

In a software project the developers are the set of resources to be allocated to various tasks described by [11]. The developers possess a specific skill or a set of skills. Each developer has an expertise in integer value associated with a skill that he needs to complete an allocated task. This can be represented like this:

• 1.  D is the set of developers each denoted by D_i,

• 2.  S is the set of Skills required to complete the

• 3.    T is the set of tasks done to complete the software project. Task T 0 represents the beginning of the project and T t represents the end of the project. Each task is identified with T i where i=1 to t.

• 4.  E ij is the expertise value in integer associated a

• 5.    DS is an ordered pair set (S j ,E_i j ) where E_i j is expertise possessed by D_i for skill S j where D_i ∈ D and S i ∈ S.

where i=1 to n.

project. Each skill is denoted by Si where i=1 to m.

task T i that requires skill S j to accomplish the task. T i ∈ T and Si ∈ S.

• B.    Assumptions

• •    The tasks are to be executed in a specific sequence and a successor and predecessor of a task cannot be violated.

• •    The cost of the task is not considered in current problem, only criticality of completion of project is considered here.

• •    A relationship exists between the task duration, skill required and expertise level of the developer. It can be defined as function of Skill required for

task T_i and expertise value processed by developer D j.

Where S_ik is the skill i required for accomplishing task k and R_k j is the skill expertise possessed by the Developer j for with respect to skill k. Duration of completion of task k is computed by this function that evaluates on the skill acquired by the developer to accomplish task.

• C.    Objective Function

Problem is to minimize the duration of the complete project. The constraints on the resources are defined as:

f ( x )=∑   Dur(Ti)           (2)

• •    Minimize function f(x) for all the tasks T_i in the project.

• •    One task is undertaken by one developer at a time depending on the skill required.

• •    All the skills needed for a specific task must be predefined.

Each skill associated with a task must be quantified by the expertise required in number. Only a developer with equal of higher degree of expertise can be allocated the task of the number of skills measures the degree of specialization of the knowledge.

• IV.    The Proposed Solution

After understanding of the elements of the problem, the next step is defining the solution space elements. The solution of the resource constrained scheduling for a software project is defined by a matrix M=mij where mij is the duration to be taken by developer di to complete the task Tj. This matrix is updated with the input of developer skills and the task-skill mapping:

	T1	T2	T3	T4	T5	T6
D1	m11	m12	m13	m14	m15	m16
D2	m21	m22	m23	m24	m25	m26
D3	m31	m32	m33	m34	m35	m36
D4	m41	m42	m43	m44	m45	m46
D5	m51	m52	m53	m54	m55	m56
Mij= <	Value in hours for the developer Di possessing the expertise of skill required for the task for task T j

0 otherwise

Each task in this matrix is initially set to zero. The task relationship is defined by a directed acyclic graph. Each node is defined as task, the arc joining the nodes show the predecessor and successor relationship. By defining this relationship between the tasks the start time and end time of each task is calculated. This calculated duration is used to evaluate the total time it will take to complete the project. The solution is defined by the sequence of tasks undertaken by the developers with required skills so that the total time of the project is minimum.

Fig. 1 shows the tasks for a dummy project P with tasks T1 to T6. T0 and TF are the start task and the end tasks. Each task is specified along with the skill expertise required for the task. The task can only be assigned to a developer with expertise value equal to or greater than the required expertise as mentioned in the job requirement.

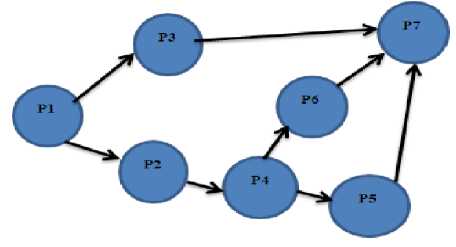
Fig.1. Relationship and precedence of the tasks.

Table 2. Task parameters for scheduling of dummy project P based on the fictitious values of the skill parameter

1	2	3	4	5	6
Task	Skill require d	Expertise Level Needed for skill (0-5)	Duration (in man hours) Function of (column 2,3)	Start Time	End Time
T1	S1	2	240	ST1=0	ET1=ST1+240=240
T2	S2	4	110	ST2= 240	ET2=240+110=350
T3	S3	3	20	ST3=0	ET3=ST3+20=20
T4	S4	3	300	ST4=ET3=20	ET4=ST4+20=320
T5	S5	2	60	ST5=ET3=20	ET5=ST5+60=80
T6	S6	3	400	ST5=max(ET2,ET5, ET6)=max(350,320, 80)=350	ET5=ST5+400=750

Table 3. Developers, Skills possessed and Expertise Level for Dummy Project P

Developer	Skills	Expertise
D1	S1,S3,S5,S6	3,3,3,3
D2	S2,S4,S6	5,4,2
D2	S3,S4,S5	5,5,5

A. Proposed Genetic Algorithm-based solution to schedule a resource constrained software project

Genetic Algorithms are complex problem solving algorithms that represent the real world problems as biological evolution processes as used in [9]. At the very first stage of GA a solution or population is formulated by a defined technique like greedy method, backtracking method or branch and bound technique. The GA algorithm is then applied on this population to generate more population with the target of achieving better populations that evaluate better on the objective function of the problem in hand. The main techniques used in this evolution are combining of solutions, with the help of genetic operators for selection, crossover and mutation.

The Genetic Algorithm is a widely used is a population-based optimization technique which is used in solving numerous complex problems of NP-hard nature like travelling salesman, Hamiltonian graphs, n-graph color etc. The algorithm is based on the process of natural selection as demonstrated by animals to find best survival chances in the current circumstances. Designed on the GA algorithm, the solution to the resource constrained project scheduling problem for software projects, each possible schedule is defined as one solution. Before the execution of the GA on the current solutions the total solution counts, the probability values associated with crossover and mutation to compute new genetic operator and generation count are defined.

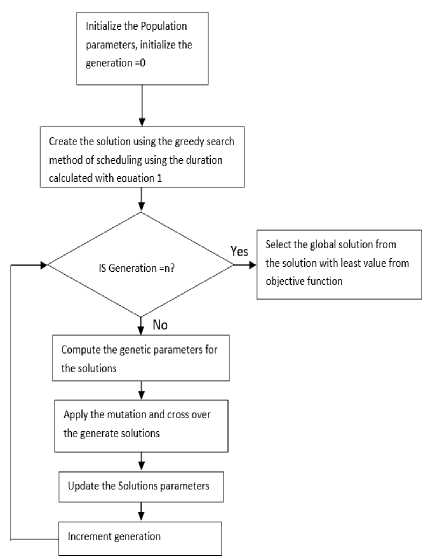
Fig.2. Flowchart for GA based solution to the RCPSP in Software projects

The proposed solution to the Resource constrained Project Scheduling Problem of software projects is defined with the following flowchart in Fig. 2. Each solution is a schedule which consists of sequence of activities. The solutions are evaluated on a fitness function that defines its fitness to the final solution space which is an objective function. After each iteration, each updated solution is evaluated to compute the fitness values. On the basis of previous generation, the genetic operators are defined.

• V.    Validation and Implementation

In this section validation and implementation, the resource constrained project scheduling problem RCPSP has been implemented using genetic algorithm and validated using test cases and data. The algorithms are tested and validated using MATLAB tool in terms of performance, time complexity and flexibility. The results of the algorithm are compared with the previous algorithms like NP hard problem and graph coloring problem and it clearly indicated our genetic algorithm are far better in terms of number of iteration taken to solve the RCPSP. The performance and time complexity is also better and suited for software development model.

• A.    Performance Analysis

The resource constrained project scheduling algorithm has been developed in to a MATLAB code and performance tested was conducted to check the efficiency of the RCPSP. The algorithm was designed by considering all the points in genetic algorithm. The main idea which was considered while testing the code was mutation and crossover solutions. By applying mutation and cross over in resources constrained project scheduling problem in software development projects gave very good performance in terms of time and resource allocation. After testing the code using genetic algorithm concepts, we gathered the data in the process of iteration. The iteration of Matrix i,j provide optimal time to process the data and give optimal solution.

• B.    Design of Coding and Analysis

The main concepts of proposed solution are directly converted into MATLAB code. The idea here is to allocate the less available resources to produce maximum results. The maximum results are in terms of completing the project successfully on time. In software development projects where there will be set of people to complete the project with limit amount of resources like system, skill sets, time, budget etc. so everything is converted into individual data sets to test and validate the scenario.

Here to complete a software development project the things that were considered are list below. They are developers, skills set, expertise level and start time of the project, end time of the project and resources available at current time. Here, D is the set of developers and they are denoted by Di. Then S is the skill set required to complete the project on time and each skill set is denoted by Si. T is the number of task which needs to be completed. Then the next parameter is expertise level and it is directly associated in integer values. The expertise values are starting from 0 and end at level 5.

Table 4. Shows the parameters and values needed to test the code

Parameters	Values
Developers	D1, D2,D3,D4,…
Skill Set	S1,S2,S3,S4,S5,…
Expertise	Level 1to Level 5
Project start time	0 (can be integer number if started late)
Project Duration	Project start time + Project duration
Resources	All the parameters are resources

• C.    Results and Comparison of Algorithms

The result shows the objective function taken to solve the NP hard problem is success and verified successfully. The number of iteration to solve the NP hard problem relies on the task level, and time duration of the project with minimal resources. The genetic algorithm for RCPSP has been compared with other standard algorithm like graph coloring problem and minimum search tree algorithm. While comparing the results the RCPSP shows greater performance in terms of time and scheduling resources. The lesser the time taken to schedule the resources the lesser the time taken to complete the software project.

Improving the genetic algorithm for RCPSP, we use the standard replacement mechanism of genetic algorithm. This means there is a possibility of replacing previous algorithm with best fit algorithm for software development problem. In the results fitness scaling method is used to maximize numerical function of genetic algorithm in this project, we like to include the corresponding fitness function f. This fitness function needs to be positive so that we can use fitness proportionate selection scheme.

We define the fitness function as f(x) = F(x) – Fmin. The f(x) function guarantees that our fitness function is always positive. If in some case fmin value is unknown in some cases before hand, we have to define f(x) = F(x) – Fmin, where x min is the individual with lowest fitness function evaluated so far.

In our case of RCRSP, we have to define the effects of making good value of x, so that it is not hard to distinguish fmin. After running the genetic algorithm for some number of iteration, the fim value reduces the scheduling problem towards better individuals. From the results, the value of fmin reduces after each iteration. This reduces the time to allocate resources in a time efficient way. The result of iteration shown above is the part of iteration process. The iteration can go up to more numbers depend on the number of available resources and project time. Because of the parallel genetic algorithm; we have two mechanisms called centralized and distributed reproduction. The evaluation of fitness function is distributed over available resources.

The numbers in the iteration results are not really a large number; we will take one set as an example and explain the main context in the results as shown in fig. 3 and fig. 4.

Table 5. Shows Number of Iteration taken to Schedule the resources to developers

Iteration: 0

xmin: [462.548187631096 f(xmin): 8442.0384	101.343106775156	118.575085241854	66.0189178029721	56.8098630355186	79.9880556590845] --
Iteration: 1 xmin: [462.548187631096 f(xmin): 8442.0384	101.343106775156	118.575085241854	66.0189178029721	56.8098630355186	79.9880556590845] --
Iteration: 2 xmin: [462.548187631096	101.343106775156	118.575085241854	66.0189178029721	56.8098630355186	79.9880556590845] --

f(xmin): 8442.0384

Iteration: 3

xmin: [500 96.3172869560601 119.702750725974 63.7046804210173 50 73.8519231107654] -- f(xmin): 8419.0346

Iteration: 4

xmin: [500 92.3066156069603 131.195247298687 50 50 76.3447551548309] -- f(xmin): 8405.6388

Iteration: 5

xmin: [500 91.2623027505271 141.861376951594 50 50 74.6598268669698] -- f(xmin): 8399.5777

Iteration: 6

xmin: [500 90.4603852129967 143.484836965913 50 50 74.6924583433636] -- f(xmin): 8399.1581

Iteration: 7

xmin: [500 87.956566637512 138.697855604933 50 50 74.0144441612375] -- f(xmin): 8397.0156

Iteration: 8

xmin: [500 82.7214775839979 137.810046574346 50 50 69.655350328315] -- f(xmin): 8387.6474

Iteration: 9

xmin: [500 73.3608314756612 139.452713730243 50 50 66.6964885461541] -- f(xmin): 8382.0973

Iteration: 10

xmin: [500 68.98835792185 143.550055383791 50 50 63.1934680688945] -- f(xmin): 8376.0069

Iteration: 11

xmin: [500 68.98835792185 143.550055383791 50 50 63.1934680688945] -- f(xmin): 8376.0069

Iteration: 12

xmin: [498.243199595057 65.6454119217775 147.885832230003 50 50.9652467525378 62.1477419229188] -- f(xmin): 8373.7495

Iteration: 13

xmin: [498.243199595057 65.6454119217775 147.885832230003 50 50.9652467525378 62.1477419229188] -- f(xmin): 8373.7495

Table 6. Data given into the MATLAB code

1	2	3	4	5	6
Task	Probabilit y	Expertise Level Needed for skill (0-5)	Duration (in man hours) Function of (column 2,3)	Start Time	End Time
T1	0.07	2	240	ST1=0	ET1=ST1+240=240
T2	0.0095	4	200	ST2= 240	ET2=240+110=350
T3	0.009	3	220	ST3=0	ET3=ST3+20=20
T4	0.009	3	220	ST4=ET3=20	ET4=ST4+20=320
T5	0.008	2	220	ST5=ET3=20	ET5=ST5+60=80
T6	0.0075	3	120	ST5=max(ET2,ET5, ET6)=max(350,320, 80)=350	ET5=ST5+400=750

Iteration: 1

xmin:     [462.548187631096     101.343106775156

118.575085241854                66.0189178029721

56.8098630355186  79.9880556590845]  -- f(xmin):

8442.0384

In this xmin matrix, [462, 101, 118, 66, 56, 79] – fxmin. The values are considered without decimal points. The value of fxmin reduces after each iteration and it would reduce to larger extent after 220 iterations. This iteration process does not take much time but it reduces the fxmin value. This indicates that time required to schedule the resources is effectively decreased after each iteration.

data=	[0.007	2	240	0	240
	0.0095	4	110	240	350
	0.009	3	20	0	20
	0.009	3	300	20	320
	0.008	2	60	20	80
	0.0075	3	400	350	750] ;

###### RESULT #########

Objective function for xmin: 8352.6109

xmin:        [463.348719683679        76.685693692945

158.435866567688   50.0000000000004   51.9765335546934

50.0000000000006]

F = 8.3526e+003

P1 =   323.6373   76.6857  158.4359   50.0000   51.9765

50.0000

Lam = 1.342

• Fig.3.    Fxmin value and number of iterations

The value of fxmin reduces and stabilizes after particular iteration. Our genetic algorithm is compared with graph coloring problem and spanning tree problem.

###### RESULT #########

Objective function for xmin: 19392.65 xmin: [55.0058483897374 240 0 20 20 350]

F = 1.9393e+004

P1 =  100.0000 240.0000     0 20.0000 20.0000 350.0000

lam = 8.9199

• Fig.4.    Comparison of different data set and values

It is concluded, after comparing the different data sets for our RCPSP (genetic algorithm), that the fxmin value gives the total numbers of seconds to complete a project. Time to schedule is directly proportional to the time to complete a project. The project completion depends on the team member involvement and the time to complete a project.

• A.    Crossover

In our genetic algorithm for RCPSP, an operator (crossover) constructs 2 offspring. Each offspring is formed by two parents. One-point crossover is the simplest form of crossover. The one-point crossover has an integer position called k, which is chosen randomly. The strings are created by swapping the characters from position K + 1 and length l. In our project, crossover has been applied with probability greater than 0.5. Mostly the strings are derived from the parents, in few cases it is directly derived from one parent.

• B.    Mutation

The crossover and the mutation are the two main things need to be taken in the proposed genetic algorithm. Mutation is applied to random strings and individual strings. Mutation does consider the position of the strings which are changed.

• C.    Case Study

A case study is taken to solve the software development project using RCPSP algorithm. To develop software in TCS Company, project head has the responsibility to allocate various projects to the team lead. The team lead has to consider the amount of time to develop the software, number of developer with proper skill level, expertise level in each team. Here, the main problem is the time that will be consumed to schedule the resources to team members. Our proposed genetic algorithm solves the RCPSP problem to schedule resources to team members. To make this happen, team lead should have the proper idea and knowledge of team member skill sets, expertise level and time to complete the project. Team lead runs the code and allocates necessary resources to the team member to complete the project on time successfully. Our proposed algorithm will consider all the parameters to schedule resources to the team members to complete a project successfully on time.

• VI. Conclusions

In this paper, resource constrained project scheduling solution has been given and solved using genetic algorithm. The algorithm is designed and tested using MATLAB. The results give a clear indication that run time complexity of scheduling is reduced to great extent. The assumptions and data sets are implemented and tested to prove that the algorithm works well and it addresses the resource constrained project scheduling problem of software industry. Due to resource constraint environment, the complexity of algorithm increases exponentially. But the proposed algorithm is a better solution as compared to the traditional methods. The Genetic Algorithm also solves the problem of multiple resource constrains project scheduling. This typical NP hard problem is solved via mathematical model using genetic algorithm. The data sets of software development projects are considered to check the efficiency of proposed algorithm.