Novel Reversible DS Gate for Reversible Logic Synthesis

Автор: Shaveta Thakral, Dipali Bansal

Журнал: International Journal of Modern Education and Computer Science (IJMECS) @ijmecs

Статья в выпуске: 6 vol.8, 2016 года.

Бесплатный доступ

Reversible logic has various applications in fields of computer graphics, optical information processing, quantum computing, DNA computing, ultra low power CMOS design and communication. As our day to day life is demanding more and more portable electronic devices, challenging focus on technology is demanding great system performance without any compromise in power consumption. It is obvious to find tradeoff between processing power and heat generation. As decreased processing speed leads to reduced power consumption but obviously compromise in performance is not acceptable for sophisticated applications. Thus power consumption is a prime target now days. Needless to say, researchers will now look at reversible logic in this vein. Primitive component of reversible logic synthesis are reversible logic gates .Thus it is very important for a new researcher to look into extensive literature survey of reversible logic gates. Many papers have been reported with review of reversible logic gates. This paper aims on updates in reversible logic gates and propose a novel reversible DS gate which will be stepping stone in design and synthesis of any complex reversible logic based synthesis.

Еще

Reversible, Power consumption, Primitive component, Optimization metrics, Reversible DS gate

Короткий адрес: https://sciup.org/15014872

IDR: 15014872

Текст научной статьи Novel Reversible DS Gate for Reversible Logic Synthesis

Published Online June 2016 in MECS

I. Introduction

In 1961, R. Landauer [1] stated that “amount of energy dissipated for every bit erasure during an irreversible operation is given by KTln2 joules where K is Boltzmann’s constant and T is the operating temperature. In 1973 C.H.Bennett [2] proposed the solution to R. Landauer statement and showed that KTln2 energy dissipation would not occur, if computation is done in a reversible manner since amount of energy dissipated in a system depends directly on numbers of bits erased during computation. Classical gates like two input AND, OR,

NAND, NOR, XOR and XNOR are irreversible as we can’t uniquely reconstruct input states from output states. Here two bit input state is mapped to one bit output state leads to erasure of one bit and consequently loss of energy. We can avoid this energy loss by mapping n bit input states to n bit output states so that input states can be uniquely recovered from output states and under such circumstances, a gate is said to be reversible. Quantum gates or reversible gates differ from Classical gates in a way that a) quantum gates work on qubits rather than bits b) feedbacks are not permitted in reversible logic circuits made with reversible logic gates so called acyclic and c) there is no fan out allowed means several copies of qubit are not allowed. It is very important to know that out of four 1*1 one qubit gates; only two are reversible i.e. trivial gate and not gate. Similarly out of 256 possible 2*2 two qubit gates; only 24 are reversible as proposed in table 1.

A. NCV Gate Library

NCV gate library contains following set of quantum gates i.e. NOT gate, CNOT gate and controlled V and controlled V ⁺ gates. Controlled V and controlled V ⁺ gates are basically types of controlled square root of NOT gates. In both of these gates, when control input is 0 then second input is propagated as it is to output, Two V gates in series operation becomes CNOT gate or inverter. Similarly two V ⁺ gates activated in series operation becomes CNOT or inverter gate and one V and another V ⁺ gate in series operation become an Identity gate or buffer. Here block diagram of a 2*2 reversible gate is presented in Fig.1 with A and B as input and P and Q as output. Here quantum implementation of NOT gate, CNOT gate and Controlled V and controlled V ⁺ gates is given in Fig.2, Fig.3, Fig.4 and Fig.5 respectively .Quantum implementation of integrated qubit gates can be implemented by cascading quantum implementation of CNOT gate with controlled V gate or with controlled V ⁺ gate.

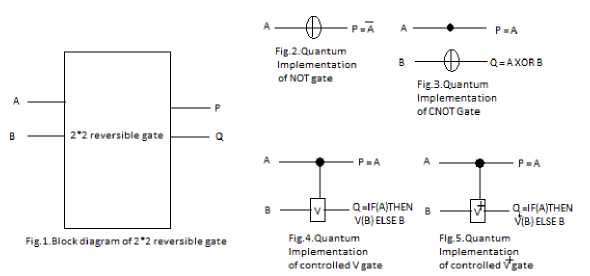
Table 1. Representation of all possible existing 24 2*2 reversible logic gates

Revers ible gate	P	Q	Reversi ble gate	P	Q	Reversi ble gate	P	Q	Reversi ble gate	P	Q
1	A	B	7	»ф В	B	13(Feyn man Gate)	A	Аф В	18	Аф В	"в
2(Swa p Gate)	B	A	8	B	а	14	B	Аф В	20	Аф В	д
3	Аф В	B	9	а	Аф В	15	А© В	A	21	а	B
4	A	Аф В	10	"в	А	16	в	Аф В	22	а	"в
5	Аф В	A	11	Аф В	li	17	A	"в	23	дф в	д’

Table 2. Fundamental 3*3 reversible logic gates

Reversible Logic Gate	Specifi cation	Expression	Quantu m Cost	Feature	Quantum Implementation
Toffoli/CCNOT Gate[3]	3*3	Р Z А QZ В П = АВфС	5	Universal Reversible Logic Gate	С------ ^v ---- ^v ---- ^v+ ----- ^R Quantum Implementation of Toff oil Gate
Fredkin Gate/CSWAP Gate[4]	3*3	Р = А Q=AB® АС R = АСфАВ	5	Universal Reversible Logic Gate, Parity Preserving Reversible Logic Gate	В--!—I _v+--1 V I1 v -----•— Q с Ф A ---1---jf------------J-----ф В Quantum Implementation of Fredkin Gate
Peres Gate/NTG[5]	3*3	Р=А а = Афв R=AB$C	4	Lowest Quantum Cost	=---------*—Ф—•---° c Q-Q—0—„ Quantum Implementation of Peres Gate
Double Feynman Gate[6]	3*3	Р = А q = a®b Н = АфС	2	Parity Preserving Reversible Logic Gate	A --------------------P в -------Q c -------------i-------R Quantum Implementation of double Feynman Gate

Table 3. Other popular 3*3 reversible logic gates

Reversible Logic Gate	Specification	Expression	Quantum Cost	Feature
BJN/MTG Gate[7]	3*3	Р =А Q = В R = \|A4 В)@С	5	Universal Logic Gate, Used for FAN OUT	А--------------•---•------- ---- Р в---*----—ф—♦— --Q Quantum Implementation of BJN Gate
YAG/UPG Gate[8]	3*3	Р -А а = (АфВ)ф(АВфС) Я = АВфС	4	AND,NAND,OR,NOR	Quantum Implementation of UPG Gate
RC-I Gate[9]	3*3	Р = А Q = АВ ф С R = АВ ф С	4	1 bit comparator	^a---------т—--------^p В------ф—» Ф 0 с—Q Q ЕМ ^R Quantum Implementation of RC-I Gate
RMUX 1 Gate[10]	3*3	Р = А Q = АВ+АС R = АС + АВ	4	Multiplexer	A ---------------■---- ------------ P В-- — ^V -- ^V--^VM--f^{- Q} C —Ф--^--------ф--1---Ф— R Quantum Implementation of RMUX1 Gate
RMUX2 Gate[10]	3*3	Р =А Q = АВ+АС Н = (Афв)фС	4	Multiplexer	В----*—I _v+\|--1 V ------1 V ----------Q c —®—J—e—1---------к Quantum Implementation of RMUX2
TR Gate(TRG)[11]	3*3	Р =А а = Дфв R=AB0C	4	Subtractor	В—1-----®—1--- a ^c4ZbQ—Q—« Quantum Implementation of TR Gate
MFRG Gate[12]	3*3	Р =А_ Q = АВ ф АС В=АСф АВ	4	Universal Logic Gate with reduced quantum cost	A ------------------------- ^P E —®---- Ф--•-Ф-- Q c —•- v - V v⁺ —•--- ^R Quantum Implementation of MFRG Gate

B. Multi Qubit Logic Gates

Here fundamental 3*3 Reversible logic gates and other popular 3*3 reversible logic gates are described in Table 2 and Table 3 respectively with their logic expression, quantum cost, and special feature respectively. To justify quantum cost; Quantum implementation of logic gates is

also given. Table 4 describes all popular 4*4 reversible logic gates and to justify quantum cost, quantum implementation is also given. Table 5 describes 5*5 reversible logic gates and to justify quantum cost, quantum implementation is also given.

Table 4. Popular 4*4 reversible logic gates

Reversible Logic Gate	Specification	Expression	Quantu m Cost	Feature
Double Peres/MTSG Gate/DPG/PFAG[13]	4*4	Р = А Q=A®B " = АфВ®С 5 = (АфВ)СфАВфО	6	Reversib le Full Adder Gate	⁶ ] м ° Quantum Implementation of HNG Gate
HNG Gate[14]	4*4	P = A Q=B П = (АфВ\|фС 5 = Йв)СфАВфО	6	Reversib le Adder	Quantum Implementation of HNG Gate
MRG Gate[15]	4*4	P = A Q=A$B "=АфвфС 5 = (АВфо)ф((АфВ)фС)	6	OR,NO R,XOR, XNOR	o--Q--Q--Q---о—s Quantum Implementation of MRG Gate
PAOG Gate[15]	4*4	P = A а=Афв Н = АВфС 5 = (АВфс)ф((АфВ)фО)	6	OR,NO R,AND, NAND	A------ ------------- --------------- ^P в--*—-- 1----- а с------ 1 v I------1 v I------- _v+--e- R D----------------------Ф—A- S Quantum Implementation of PAOG Gate
RC-II Gate[9]	4*4	Р =А а=двфо К=АфвфС S = АВ ф D	5	Reversib le sign bit compara tor	Quantum Implementation of RC-II Gate
RC Gate[15]	4*4	Р = А Q = \|A® В)ф(Вф АВ) К = В фСфм $=АфВ® □	5	Compar ator	A -------------•--•------------P в —О ^4^HH)-q C --ф- V — V--V"¹" "•— ^R 0 --------------- Ф--------s Quantum Implementation of RC Gate

Table 5. 5*5 Reversible Logic Gate

Reversible Logic Gate

Specification

Expression

Quantu m Cost

Feature

Morrison Gate[15]

5*5

Р -А

Q=A ф В

R = (А® В)$С

S = АВ фО

Т = |(АфВ) фЕ)ф(АВфО)

OR,AND

В--•-------•--- Q

Е--------------------9-------jv_T

Quantum Implementation of Morrison Gate

II. Proposed Reversible Ds Gate

There exist 16777216 different 3*3 three qubit gates however number of reversible 3*3 gates is much smaller i.e.40320.Many 3*3 reversible gates have been proposed in literature with their unique applications and quantum cost. This paper proposed 3*3 reversible gate called as DS reversible gate with its unique application for sequence generation. Fig.6 represents the block diagram of 3*3 DS reversible gate. The truth table of this reversible gate is shown in table 6. By analyzing the truth table of DS reversible gate it is identified that obtained output pattern have unique image of input pattern i.e any input pattern is uniquely determined by its corresponding output.

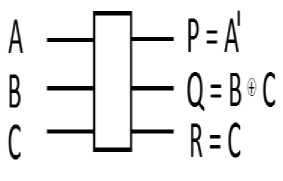
Fig.6. Proposed reversible DS Gate

Proposed reversible DS gate can be used in counters. Counter is a sequential device fabricated with flip-flop. Counter as its name indicate is a counting device which count either in increasing, decreasing and in any specific order proposed by designer.

Table 6. Truth table of 3*3 Proposed Reversible DS Gate

A	B	C	P	Q	R
0	0	0	1	0	0
0	0	1	1	1	1
0	1	0	1	1	0
0	1	1	1	0	1
1	0	0	0	0	0
1	0	1	0	1	1
1	1	0	0	1	0
1	1	1	0	0	1

Whenever any input clock pulse trigger counter then output obtains is a binary number of specified counting sequence. At every rising edge of clock pulse output of counter is the next number in sequence. There are different applications of counter for example in our daily life appliances such as microwave, washing machine where synchronous counter is used which enable timer option, in digital clocks, time interval measurement and others. Along with above discussed application this sequential device may also be used to obtain the waveform of different frequencies and pattern.

III. Comparison and Results

For obtaining result and to compare them with preexisting technique reversible ’Fredkin’ gate is used. Table 7 represents the performance of the proposed logic (reversible DS gate) over the existing method (Fredkin) using MATLAB/Simulink model shown in Fig. 7. In reversible Fredkin, reversible gate is used to obtain desired function of counter, because of its ability to consume less power .For every sequence state proposed DS gate consumed less power as shown in Fig.8.The quantum cost of proposed DS gate is 2 yet Fredkin gate has quantum cost of 5.Proposed DS gate can be realized using one NOT and one CNOT gate yet Fredkin gate is realized using 2CNOT and 1 Toffoli gate

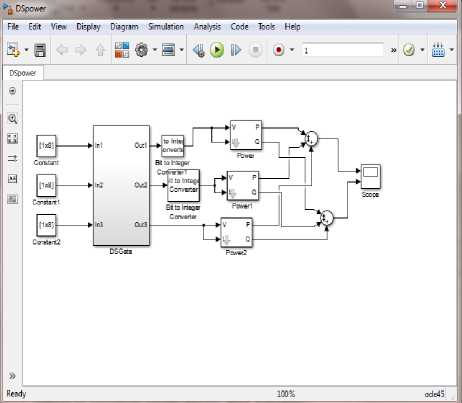
Fig.7. DS Gate Power model

Table 7. Sequence generator with their respective energy requirements

Input			DS Gate	FredkinGate
A	B	C	DS Gate	FredkinGate
0	0	0	0.000334905	0.00321154
0	0	1	0.000502357	0.06423081
0	1	0	0.000502357	0.006423081
0	1	1	0.000334905	0.009634621
1	0	0	0.000167452	0.00321154
1	0	1	0.000334905	0.006423081
1	1	0	0.000334905	0.006423081
1	1	1	0.000167452	0.009634621

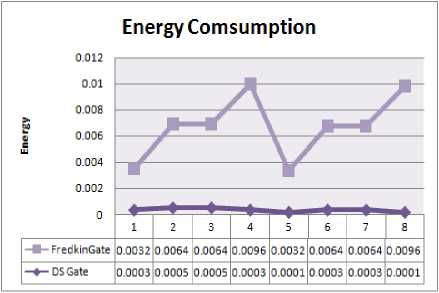
Fig.8. Sequence Generator with Their Respective Energy Requirement

IV. Conclusions

The major idea present in this paper is to propose 3*3 reversible DS gate. This proposed DS gate is useful to optimize the design of counters or sequence generator. Also by presenting the comparison result it is a clear indication that the proposed DS gate logic is better than the existing logic of counter in terms of energy consumption and garbage output. Energy efficient reversible logic is important concept and have application in various domain for example low power CMOS, quantum computing, nanotechnology, and optical computing and proposed DS gate. This proposed logic can also be used to design large reversible system. Thus, in a brief manner it concludes that the reversible logic has its benefaction in reducing the energy consumption to a great extent.

This paper is doorsill to design intricate systems that execute different complex operations. At last, we conclude by presenting comparison result of existing method (Fredkin) and proposed method (DS gate). Thus, this proposed logic is applicable in designing of the complex system used in nanotechnology. This paper aims not only on updates in reversible logic gates with their expressions, special features and quantum cost but also on their quantum implementation to justify quantum cost which are stepping stones in design and synthesis of any complex reversible logic based synthesis. A new researcher may begin with basics of reversible logic gates and implement optimum reversible logic circuit based on various optimization metrics like ancillary inputs, garbage outputs, quantum cost

Список литературы Novel Reversible DS Gate for Reversible Logic Synthesis

R. Landauer, "Irreversibility and Heat Generation in the Computational Process," IBM Journal of Research and Development, vol. 5, pp. 183-91, 1961.
C. Bennett, "Logical Reversibility of Computation," IBM Journal of Research and Development, vol. 17, pp. 525-532,1973.
Toffoli, Tommaso," Reversible computing". Springer Berlin Heidelberg, 1980
E. Fredkin and T. Toffoli, "Conservative Logic," International Journal of Theoretical Physics, vol. 21, pp. 219-53, 1980.
A. Peres, "Reversible Logic and Quantum Computers," Physical Review, vol. 32, iss. 6, 1985, pp 3266-3276
Parhami, Behrooz. "Fault-tolerant reversible circuits." Signals, Systems and Computers, 2006. ACSSC'06. Fortieth Asilomar Conference on. IEEE, 2006.
Thapliyal, Himanshu, and A. Prasad Vinod. "Design of reversible sequential elements with feasibility of transistor implementation." Circuits and Systems, 2007. ISCAS 2007. IEEE International Symposium on. IEEE, 2007.
Moallem, Payman, et al. "Optimized reversible arithmetic logic units." Journal of Electronics (China) 31.5,pp. 394-405,2014.
F. Sharmin, R. K. Mitra, R. Hasan, and A. Rahman, "Low cost reversible signed comparator," International Journal, 2013.
Morrison, Matthew, Matthew Lewandowski, and Nagarajan Ranganathan. "Design of a tree-based comparator and memory unit based on a novel reversible logic structure." VLSI (ISVLSI), 2012 IEEE Computer Society Annual Symposium on. IEEE, 2012.
Thapliyal, Himanshu, and Nagarajan Ranganathan. "Design of efficient reversible binary subtractors based on a new reversible gate." VLSI, 2009. ISVLSI'09. IEEE Computer Society Annual Symposium on. IEEE, 2009.
Nagamani, A. N., H. V. Jayashree, and H. R. Bhagyalakshmi. "Novel low power comparator design using reversible logic gates." Indian J. Comput. Sci. Eng 2.4 pp. 566-574.,2011.
Moraga, Claudio, and Fatima Z. Hadjam. "On double gates for reversible computing circuits." Proc. Intl. Workshop on Boolean Problems. 2012.
Haghparast, Majid, et al. "Design of a novel reversible multiplier circuit using HNG gate in nanotechnology." World Appl. Sci. J. 2008.
Morrison, Matthew, and Nagarajan Ranganathan. "Design of a reversible ALU based on novel programmable reversible logic gate structures." VLSI (ISVLSI), 2011 IEEE Computer Society Annual Symposium on. IEEE, 2011.

Еще

Статья научная