Novelty in Image Reconstruction using DWT and CLAHE

Published Online May 2017 in MECS DOI: 10.5815/ijigsp.2017.05.04

An image is simply what we perceive, when the rays of light fall on an object and reflection or refraction occurs. The demand of digital imaging is growing rapidly due to its applications in large number of fields where digital images may be used for detection of cancers, tumors, detection of objects under water, medical diagnosis, aeronautical imaging etc. In such cases, the quality of the information contained in the image is of utter importance so that better results can be produced. In this context, various wavelet transforms and several interpolation techniques are present which include:

• >    Wavelet Zero Padding (WZP):   It involves

appending a zero matrix at the end of the image by overlooking the sub-bands of higher frequency and then the inverse of WZP is applied to attain a higher frequency image.

• >    Wavelet Zero padding and Cycle Spinning (WZP-CS): In this, first of all, WZP is applied to attain an intermediary higher frequency image which is then decomposed into N lower resolution images by spatial shifting, after that WZP is applied on these N lower resolution images to attain N higher resolution images and finally, these are averaged and realigned to achieve the final output image.

• >    Discrete wavelet Transform (DWT):   DWT

disintegrates the given image into four sub images named as: low-low (LL), low-high (LH), high-low (HL) and high-high (HH) images. Of these, the lower frequency components are accounted to interpolation and finally inverse DWT is applied to attain the final higher frequency images.

• >    Stationery Wavelet Transform (SWT): In this, the input image is first of all directed to WZP followed by SWT to attain two sub-bands namely: estimated and approximated coefficients and finally, inverse of SWT is applied to obtain a higher frequency image.

• >    Dual Tree Complex Wavelet Transform (DT-CWT): It deals with directional sensitivity. First, the image is disintegrated into distinct sub-bands of lower and higher frequency, then, the higher frequency sub-bands are filtered followed by interpolation with lower frequency components and finally the inverse is applied to attain a higher frequency output image.

• >    SWT-DWT: It is the combination of SWT and DWT, the input image is subjected to DWT and SWT simultaneously, the higher frequency components attained from both are interpolated and finally inverse is applied to attain the output image.

• >    Interpolation: It is a technique that is used to approximate the unknown pixel data for a given image to enhance the size of the given image. The new points are determined with respect to some known points. There are various interpolation methodologies used for zooming an image. These are

• i.    Linear Interpolation:    It is the most

straightforward form of interjection that determines the neighborhood pixel points one by one linearly.

• ii.    Bilinear Interpolation: It is the advancement of linear interpolation that deals with the 2x2 neighborhood of the known data point.

• iii.    Bi-cubic Interpolation: It deals with 4x4 neighborhood but is time consuming in contrast to others.

• iv.    Nearest Neighbor: It deals with the nearest neighbors one by one and takes the least time for processing.

• v.    Higher order spline: It take into consideration, a larger domain of pixels in order to produce better interpolation results.

> Contrast Equalization: Contrast Limited Adaptive Histogram Equalization (CLAHE) method is used for the improvement of the image glare after the image enhancement. This adds to the quality of the final image produced.

• II.    Related Works

  The methodology to change digital interpolated images at higher resolution is available today. As this field was growing more and more important, advancements in wavelet domain were made by Birare et al. (2010) that lead to the introduction of a new wavelet based super resolution algorithm which used various wavelet transforms such as db-4, db-7, db-9, db-7,9, db9,7 and Haar. These methods were then analyzed by Anbarjafari & Demirel (2010) to produce a combination of a wavelet transform and an interpolation technique. The combination was applied to well-known images and results were found to be better. These methods that were applied after image rotation, now were considered for image reconstruction in frequency and spatial domains to reduce the artifacts on zooming an image by Babu and Dr. Murthy (2011). Chadda et al. (2012); Olivier & Hanqiang (2012); Abirami et al. (2013), practiced the combination of the wavelet transforms and various interpolation algorithms with different approaches that included still objects or moving objects. Sharma & Swami (2013) then introduced a new wavelet RWT and used it in combination with bi-cubic interpolation to yield better outcomes. These researches were extended for shearlet based representation along with sparsity priors by Lakshman et al. (2013). On the basis of these researches, Saranya et al. (2014), Sinha et al (2014), Tripathi et al. (2014), studied and compared various image enhancement techniques introduced till now based on their experimental values. A new approach to image enhancement was analyzed by Gayakwad & Ravishankar (2014) that took into account the glare and contrast of the image apart from its size. Further, Kekre et al (2015) introduced a hybrid watermarking technique using SVD which proved to be better and finally, Suresha et al (2016) implemented a super resolution technique using bilinear

interpolation in spatial domain. The deduced methods till date has outperformed well in producing better quality images; but cannot be used in the long run for getting a sharper, super-resolution images in medical science. Therefore, keeping all this state of information in mind, it is observed that there is an urgency to design a novel image enhancement strategy that produces best quality image on zooming and also deals with the contrast of an image after zooming apart from just the details contained in it.

• III.    Discrete Wavelet Transform

The DWT takes discrete sets of wavelets on an image and translates it in a defined format on the basis of described rules. It divides the image into 4 sub-bands which can be evaluated individually using different set of values applied on each band. The sub-bands are usually low and high filters, i.e. , LL , LH , HL and HH , where ‘L’ , ‘H’ denotes low and high filters, respectively. The low pass tells averaging group of pixels, whereas high pass stores error of low passes. DWT is calculated using a sequence of filters. Therefore, the samples are made to pass through low pass resulting into –

q [n] = ⁽p xf)[n] = ^ T- t p p[ff[n-i ]   (1)

This signal is decomposed simultaneously by high pass giving out the detailed coefficients (of high pass) and approximate coefficients (of low pass). But since, half of the sample values are discarded due to the removal of half signal frequencies (Nyquist rule); the filter is subdivided into 2 – qi о w И=Е T - t p[i]i[2n-i]        (2)

q _hig_h [n]=Z T t P [i]f[2n-i]        (3)

This has resulted into decomposing signal in half time with characterizing signal producing double frequency resolution. The wavelet is constructed with a scaling function for resizing images. Thus, the output image of DWT is –

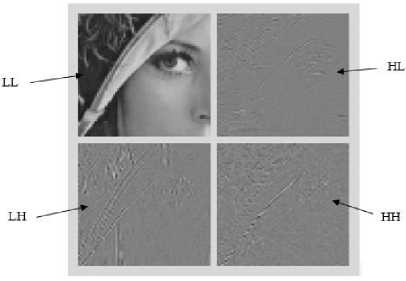
Fig.1. Output Image of DWT

The inverse DWT is applied to reconstruct original wavelet. It is considered that for applying the inverse of the same wavelet; is used for better image restoration.

• IV.    Image Quality Parameters

Peak Signal to Noise Ratio (PSNR) describes the ratio between the maximum possible power and power of corrupted noise (affecting fidelity of representation). It is usually represented on the decibel scale. In general, higher the PSNR value, the analyzed zooming quality will be higher. The PSNR is calculated using Mean Squared Error (MSE) . The mathematical representation is given by

=  ∑   ∑  ‖( , )- ( , )‖

=20 log  (√   )

This can also be represented in a text based format as:

=(  )×    (   (( - )))

×

=20×log (   (   ()))

(() where ‘e’ represents original image’s matrix data, ‘f’ is degraded image’s matrix data, ‘k’ denotes number of rows, ‘l’ is number of columns of image and ‘MAXe’ is the maximum pixel value.

• V.    Proposed Algorithm and Experimental Results

The image zooming algorithm emphasizes finding unique values of an image on the basis of PSNR. The application of DWT is applied using a discrete set of wavelet scales and is translated with predefined rules. The resultant values are compared with original images to check the algorithm’s efficiency. They rely on the objective of being with the fact that more the PSNR value; the quality resolution and property of the image increases. The algorithm is the combined method of DWT and interpolations like linear, bilinear, bi-cubic, nearest neighbor, spline; and is as follows:

start

A ^ image

Decompose ‘A’ into four sub-bands say (a1, a2, a3, a4) using DWT with ‘haar’ wavelet for i = 1,..,3 // differentiating R, G, B colors of each of 4 sub-bands

b[i] ^ a1(:,:,i)

c[i] ^ a2(:,:,i)

d[i] ^ a3(:,:,i) e[i] ^ a4(:,:,i)

end for for i =1,..,3 // interpolation applied on each sub-band w1[i] = interpolate(b,i) //using spline, cubic, bicubic, nearest, linear or bilinear w2[i] = interpolate(c,i)

w3[i] = interpolate(d,i)

w4[i] = interpolate(e,i)

end for for i =1,..,3

Combine the updated sub-bands into single image using inverse DWT end for calculate PSNR (A, X) //finding PSNR for zooming factor apply CLAHE (A) // applying contrast equalization on original and output images apply CLAHE (X)

end

The proposed methodology is tested upon several renowned benchmark images and their PSNR values have been recorded. For this purpose, six different images have been considered as input which are as shown in Fig. 2.

(I)

(III)

(V)

Fig.2. Original images (I) Airplane (II) Baboon (III) Football (IV) Lena (V) Peppers (VI) Trees

These input images are accounted to DWT along with spline interpolation and the final output images are attained whose PSNR values are recorded. The implementation results are described in Table 1. Here, the table describes the PSNR values which are calculated among original and output zoomed images.

Table 1. Calculated PSNR measures for DWT in combination with different Interpolation Techniques.

Images	Techniques in combination with DWT
	Linear	Bilinear	Nearest	Cubic	Bi-cubic	Spline
Airplane	74.8232	72.9779	72.8927	72.8927	70.9929	76.4764
Baboon	69.999	68.9269	68.6571	68.7394	67.8010	70.5864
Football	76.8462	71.6977	74.8436	75.5388	74.2762	77.2824
Lena	75.9232	74.4171	74.2504	74.2795	73.0169	77.0054
Peppers	78.1372	76.2292	75.6108	76.1788	74.2370	79.8384
Trees	72.3439	70.0172	70.265	69.9119	67.9952	74.4552

The results presented in Table 1 clearly depict the dominance of DWT with spline interpolation over other types of interpolations. Thus, being the best combination of DWT with spline interpolation plays the major role in the proposed technique, therefore the output zoomed images of DWT with spline are shown in Fig. 3.

(I)

(III)

(IV)

(V)

(VI)

Fig.3. Output Images of the proposed technique (I) Airplane (II) Baboon (III) Football (IV) Lena (V) Peppers (VI) Trees

• VI.    Contrast Equalization

The observed consequences clearly depict the dominance of DWT with spline interpolation over other combinations. Further, with a view to up-grade the glare and contrast of the given image, contrast equalization (CLAHE) is adopted and final PSNR values are calculated. To achieve a comparison analysis, the algorithm is practiced on the input images and then on the enhanced images (images shown in Figs. 2, 3). The PSNR values of the contrast enhanced images are compared with those of the original input images and a tabular comparison is made in Table 2. On the basis of these values the percentage improvement for each image is also calculated which justifies the performance of the proposed algorithm.

(III)

(IV)

(V)

(VI)

Fig.4. Output Images after Contrast Equalization (I) Airplane (II) Baboon (III) Football (IV) Lena (V) Peppers (VI) Trees

Table 2. PSNR values of enhanced and original images on Contrast Equalization

Image	PSNR for original image	PSNR for enhanced image	Percentage Improvement in Contrast
Airplane	9.9561	11.8787	19.3%
Baboon	18.7311	19.9413	6.4%
Football	10.7570	11.4460	6.4%
Lena	10.7067	12.6959	18.5%
Peppers	19.8613	10.9123	10.6%
Trees	19.8515	19.8823	0.15%

(I)

(II)

Table 3. Comparison of Proposed Technique with Existing Algorithms

Technique	Image C>	Peppers	Lena	Baboon	Football
Temizel et al (2005)		34.5012	35.0945	24.3773	33.661
Gupta et al. (2007)		30.9871	31.5587	24.6343	30.5541
Mueller et al (2007)		29.3916	25.1129	30.2908	30.8861
Birare et al. (2010)		35.2241	37.1285	36.221	37.2296
Anbarjafan et al. (2010)		23.8014	26.6743	18.0222	28.7712
Olivier et al. (2012)		34.2996	33 7806	35.944	34.7829
Lakshman et al. (2013)		34.1198	31.9761	31.2981	33.8765
Shanna et al (2013)		32.8012	33.0854	29.3333	32.6443
Saranva et al (2014)		27.0154	26.8633	27.4431	25.4421
Sinha et al. (2014)		27.4432	298781	254431	25.6651
Proposed Algorithm		79.8384	77.0054	70.5864	77.2824

The observed values in Table 2 and Fig. 4 clearly show the improvements in corresponding PSNR measures which prove the dominance of the postulated methodology over the currently existing strategies. According to the values in Table 2, the maximum percentage improvement is 27.2% and the average percentage improvement is 13.26% that can be achieved using the proposed methodology. Thus the overall result analysis depicts the improvement in quality and nature of the output images.

• VII.    Comparison With Existing Algorithms

The results shown in the previous sections have clearly highlighted the dominance of the proposed strategy. On mathematical basis, it is necessary to compare and contrast the proposed methodology with the existing techniques developed and implemented by various researchers.

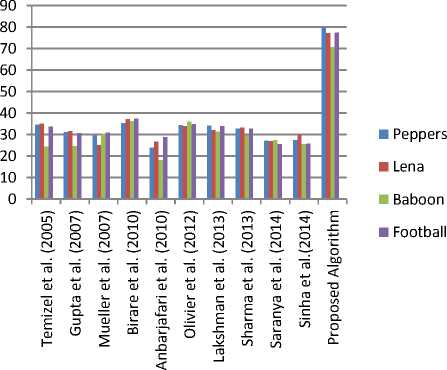
Fig.5. Graphical analysis for comparison of proposed technique with existing algorithms

Hence, the graphical analysis clearly proves the proficiency of the postulated strategy over the currently existing methodologies. It is identified that the proposed technique excels in all respects as it achieves the highest PSNR values for all the four considered images.

• VIII.    Conclusion and Future Scope

In this paper, a novel technique is postulated for image zooming, which combines the methods of DWT with interpolation techniques like spline, linear, bilinear, cubic, bi-cubic and nearest neighbor and pixel replication. Out of these, Spline interpolation with DWT comes out to be the better zooming method. The observed values of PSNR are appropriate and transformations have a positive impact on visual quality of zoomed images. At initial, only interpolation techniques were used for enhancement but are not practised widely due to its poor performance because they produce images with addition to noise or distortion. As far as DWT is concerned, it divides images into four sub-bands to reduce blurriness by applying enhancement for each of the four sub-bands. The DWT fails often to provide a good quality image as it distorts images at fewer points, generally at the corners. Therefore, in order to remove blurriness or noise related issues, interpolation techniques are combined with DWT ; by virtue of which the image is improved to a greater extent. Also, the zoomed images are free from blurriness or noise. In addition to the enhancement, the proposed technique also improves the contrast of the final images which further adds to the image quality. The results may vary precisely when used upon different versions and images. When the methods are compared with existing techniques, then to astonishment; it gives better results in terms of PSNR ( d B) values. The approach can be further used to enhance Mammography based imaging to improve upon the existing system for detecting diseases as it may necessary to get the minutest details present in the images at the time of operative measures.