Новые аналитические решения для задач колебания толстых пластин

ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2019PNRPU MECHANICS BULLETIN

Пластины широко используются как структурные элементы в дизайне конструкций. Исследованию их статических и динамических характеристик посвящено большое количество публикаций, начиная с ранних работ С.П. Тимошенко [1] и заканчивая современными исследованиями. При этом точные решения задач о колебаниях и устойчивости в механике твердого тела встречаются достаточно редко. Практически большинство известных решений были получены еще на этапе становления теории упругости и выполняют на сегодняшний день роль эталона, с которым сверяются численные и аналитико-численные методы.

В теории толстых пластин Тимошенко, в частности в теории Рейснера–Миндлина [2], даже в случае простейшей прямоугольной области точное аналитическое решение возможно лишь для пластин с двумя противоположными шарнирно-опертыми краями [3–5]. Как правило, приближенное решение для иных граничных условий строится в аналитической форме на основе вариационного подхода [6]. Заметим, что при возрастании частоты колебаний приходится увеличивать и число базисных функций, вовлекаемых в решение, в итоге порядок системы линейных уравнений относительно неопределенных коэффициентов достаточно быстро возрастает. При анализе отдельной пластины данная трудность легко преодолима, однако использование подобных решений для описания структурного элемен- та в рамках таких методов, как Continuous Element Method [7], Spectral Element Method [8], Dynamic Stiffness Method [9–15], оказывается неэффективным. В связи с этим возникает потребность в получении новых аналитических решений, которые смогли бы обеспечить требуемый компромисс между точностью решения для элемента и эффективностью численной реализации при расчете ансамбля пластин. Преодоление данного ограничения связано с новыми аналитическими решениями для динамических элементов, то есть с разработкой подхода к решению задач колебания и устойчивости теории толстых пластин, позволяющего описать поведение динамического элемента в любом требуемом диапазоне частот. В этом контексте новые решения для структурных элементов дают возможность более эффективного анализа практически значимых задач, в том числе и на основе метода спектральной динамической жесткости.

Вопросам построения эффективных аналитических решений для пластин, которые не имеют заделки в виде шарнирного опирания, посвящено большое количество исследований. Дискуссия о возможности построения точных решений продолжается до сих пор. Так, например, в недавних работах Y. Xing и B. Liu [16, 17] предлагается спорный метод «dual separation of variables», посредством которого авторы строят замкнутое аналитическое решение задачи о колебаниях полностью защемленной толстой прямоугольной пластины.

В относительно недавних работах для анализа свободных колебаний прямоугольных пластин Миндлина используются как аналитические, так и численные подходы. Среди этих работ можно отметить работы D.J. Gorman [18, 19], в которых на основе метода суперпозиции строятся аналитические решения для пластин Миндлина с различными граничными условиями, в том числе для пластин с упругой заделкой. В работе Liew и др. [6] получены собственные частоты колебаний на основе pb-2-метода Релея–Ритца; Cheung и Zhou [20] использовали в качестве базиса метода Релея–Ритца статические балочные функции, Saha и др. [21] представили новый класс базисных функций метода Релея– Ритца для пластины со свободными сторонами. В работе [22] для анализа свободных колебаний толстых пластин был предложен DSC-element Method. В работах [23–25] представлена модификация Dynamic Stiffness Method для изотропных толстых пластин, развитая на основе аналитических решений [18].

В данной статье предлагается использовать в качестве базисных функций метода суперпозиции модифицированные тригонометрические функции [26, 27], дающие возможность получить аналитическое решение задачи, описывающее все четыре типа симметрии напряженно-деформированного состояния пластины. Указанный подход впервые позволяет свести исследование задачи о собственных колебаниях толстой ортотропной пластины для случаев полностью защемленных и свободных краев к бесконечным системам линейных алгебраических уравнений и построить эффективный алгоритм определения собственных частот и форм колебаний пластины.

правлений координатных осей x и y , модулей сдвига G ₁₂ и G 13 , G 23 и коэффициентов Пуассона v ₁₂ и v ₂₁. Рассмотрим частный случай ортотропии материала, когда G 12 = G 13 = G ₂₃. Согласно принципу Бетти

E 2 ^V 12 = E 1 ^V 21

материал пластины описывается четырьмя упругими постоянными.

Следуя теории толстых пластин Рейснера–Минд-лина [1, 4], компоненты вектора смещений можно записать в виде

U ( x , y , z , t ) = u 0 ( x , y , t ) + z Ф x ( x , y , t ), V ( x , y , z , t ) = v 0 ( x , y , t ) + z ф У ( x , y , t ),

W ( x , y , z , t ) = w ⁰ ( x , y , t )

Теория Миндлина предполагает, что элемент пластины смещается в прямолинейном направлении относительно срединной поверхности пластины, но, в отличие от классической теории пластин, это направление не является обязательно перпендикулярным к срединной поверхности. Данное предположение приводит к двум дополнительным степеням свободы относительно углов поворота, в силу чего углы поворота ф x и ф У могут рассматриваться как независимые функции.

Как известно, силовые характеристики (моменты, сдвиговые силы) могут быть выражены в форме

Mx = Dx — + Dn x 1                12

д x

дф У _; д у ’

дф0     дф“ фx         y

M y D 12 ,   ⁺ D 2 ,   ;

д x       д у

1. Основные уравнения и общее решение задачи

На рис. 1 представлена прямоугольная пластина {( x,y ) е [ - a ; a ] x [ - b ; b ]} толщиной h . Упругие свойства материала можно описать при помощи технических упругих констант: модулей Юнга E ₁ и E ₂ вдоль на-

M xy

= D^

дф 0 дф 0

_+L. + i д y дx

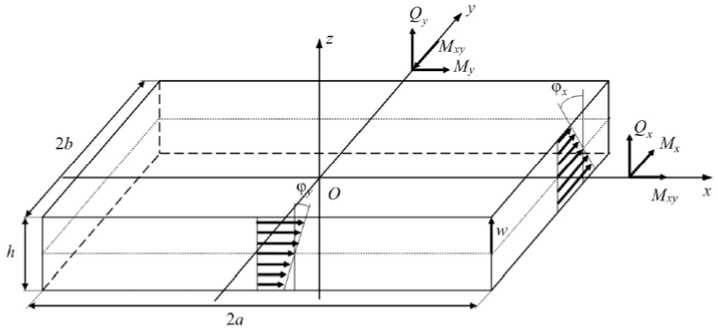
Рис. 1. Координатная система и обозначения для смещений и сил

Fig. 1. Coordinate system, forces and displacements of a plate element

где κ – коэффициент сдвига; D ₁, D ₂, D ₁₂, D ₆₆, A ₄₄ и A ₅₅ – упругие константы, связанные с техническими константами следующим образом:

D 1 =--- h E , ---. d 2 =--- hE ---; D 2 = h v 1 E 2   ;

12(1 -v 1 v ₂) ^;        12(1 -v 1 v ₂)         12(1 -v 1 v ₂)

h ³ G ₁₂

D 66 = 12 ; ^A 44 = ^K hG 13 ; A 55 = ^K hG 23 .

Уравнения свободных колебаний пластины dMx  'Mxy - Q = ph ф

8x dy L 12 dt2 ’ dMxy + dMy - Q = ph3 d2фУ

8x     dy     y 12 dt2 , d Q  dQy     22 w0

x^^ +    = p h

8 x    d y       dt²

в случае гармонических колебаний ф0 (x, y, t) = = Фx (x, y)ei™t, фУ (x, y, t) = фy (x, y)e1 mt и w0(x, y, t) = = W(x, y)e1 “t принимают вид циентами. Действительно, пусть члены первого ряда (тригонометрического по координате x) имеют вид

Wk2' = A Н- (py) Tk (ax), фX1>J = B Hj (py )T> x), (6) фУХ = CHJ( РУ )Tk(ax), где a - некоторая константа разделения, обеспечивающая полноту решения на границе пластины, а тригонометрические и гиперболические функции в зависимости от четности имеют вид

Н ₀ = ch ( z ), Н 1 = sh ( z ), T ₀ = cos( z ), T 1 = sin( z ).

Подстановка (6) в систему (4) приводит к системе линейных алгебраических уравнений относительно A , B и С :

a k ₄ A - ( k ₆ p ² - a ² - k ₄ + Q h ) B - a pkC = 0,

< pk ₅ A + a pkB - ( k ₂ p ² - k ₆ a ² - k ₅ +Q 4 ) C = 0,    (7)

( k ₅ p ² - k ₄ a ² +Q ⁴ ) A -a k ₄ B + pk ₅ C = 0.

Для существования ненулевого решения (7) необходимо, чтобы определитель данной системы был равен нулю:

k ₂

Ф+k6      +■ dx2      dy2     dxdy

^{- k} 4

8 W     1     4 n

—— + ^ф x l. ^Q h ^Ф x = 0,

8 x     J

det y k 5 p p

^{a k} 4 pk ₅

- k ₄ a ² +Q ⁴

k ₆ p ² -a ² - k ₄ +Q 4

-apk ak 4

k ₂ p ²

a pk

- k 6 a - k 5 + Q h

^- pk 5

= 0, ⁽⁸⁾

^d 2 Ф y dy²

^{+ k} 6

^{d 2 ф} y ~ d ² ф _x (d W 1    4   _

"TT ^{+ k} "^T^- ^k 5 Н^ ^{+ ф} y l ^{+ Q} h ^ф y = ⁰ , ⁽⁴⁾

8 x 6 x d y yd y J

что дает характеристическое уравнение для определения коэффициентов p :

, ( 8 ² W дф_х) .

^k 4 I          '         l ^{+ k} 5

У 8 x

8 x

.5 ' W . ^Ф    .q- W = 0,

У 8y    8y J

c 0 P⁶ + C 1 p ⁴ + c 2 p ² + c 3 = 0,              (9)

ρ h ω²

где Q ⁴ = ---- D 1

,

Q 4 = — Q ⁴ h 12

– частотные параметры;

_k = D _k = ’ ■■ _k = A k = D _k = D 66 + D 12

²     D ₁ , ⁴     D ₁ , ⁵     D ₁ ,    ⁶     D ₁ ,            D ₁     .

Общее решение уравнения колебаний строится в виде ряда частных решений с неопределенными коэффициентами согласно методу суперпозиции.Здесь предлагается следовать подходу, который был развит в теории тонких пластин [26–28]. В частности, для толстой пластины общее решение уравнений (4) может быть представлено в виде суммы четных и нечетных составляющих по каждой из координат:

( ^W 1

Ф x уф y J

= z

k , J" =0

( W l

^Ф x , Уф y , k -J

где W ₀₀ является четной по обеим координатам; W ₀₁ – четная по х и нечетная по y и т.п.

Используя стандартную технику разделения переменных, общее решение уравнений колебаний (4) для каждого случая симметрии можно записать в форме суммы двух рядов Фурье с неопределенными коэффи-

где c0 = k 2k5k6,

c 1 = a ² ( k ₅ ( k ² - k ₆ ² ) - k ₂ ( k ₅ + k ₄ k ₆ ) ) + + Q 4 k ₅ ( k ₂ + k ₆ ) + Q ⁴ k ₂ k ₆ - k ₂ k ₄ k ₅,

c ₂ = a ⁴ ( k ₄ ( k ₂ + k ₆ ² - k ² ) + k ₅ k ₆ ) +

+ a ² ( Q ⁴ ( k ² - k ₆ ² ) - k ₅ Q h ( 1 + k ₆ ) - k ₂ ( Q ⁴ + k ₄ Q h ) +

+ k ₄ ( 2 k ₅ ( k ₆ + k ) - k ₆ Q 4 ) ) + Q ⁴ ( Q h ( k ₂ + k ₆ ) - k ₂ k ₄ ) + + k 5 ( Q h ( Q h - k 4 ) - k 6 Q ⁴ ) ,

c ₃ = -a ⁶ k ₄ k ₆ + a ⁴ ( - k ₄ k ₅ + k ₆ Q ⁴ + k ₄ Q h ( 1 + k ₆ ) ) + + a ² ( q⁴ ( k 5 + k 4 k 6 - Q h ) +

+ q 4 ( k 4 k 5 - k 6 Q ⁴ - k 4 q 4 ) ) + q⁴ ( q 4 - k 4 )( q 4 - k 5 ) .

Характеристическое уравнение (9) является бикубическим и допускает точное решение по формулам Кордано [29]:

p , ( a ) = X⁺+^

c ₁

3 c 0^;

Р 23 ( a ) = -    2 ^: - 3C; ¹ 23 ^-^,    (10)

где

^ ± = "yjri^irf + s p ;

r = C ^ _ c _; _ ; s = c 2 _ c 2        (11)

^p 6 c ₀²2 c ₀27 c ₀ ^{3 p} 3 c ₀9 c ₀².

Тогда нетривиальное решение системы (7) можно найти для каждой ветви l = 1, 2, 3 корней уравнения (9) в форме

A ^{( a )} =

kk 5 p l - k 4 ( k ₂ p 2 - k 6 a ² - k 5 + Q 4 ) p , ( kk ₅ p l - kk 4 a ² + k ₄ k ₅ + k Q ⁴ )

Bt ^{( a )} =

k 52 p l + ( k ₂ p l - k 6 a ² - k 5 + Q 4 )( k 5 p l - k ₄ a ² + Q ⁴ ) a p , ( kk 5 p l - kk ₄ a ² + k 4 k ₅ + k Q ⁴ )

, (12)

C l ( a ) = 1.

d ₀ q ⁶ + d 1 q ⁴ + d ₂ q ² + d ₃ = 0,             (18)

где d 0 = k4 k6, d 1 = в 2 (k4 (k 2 - k62 - k 2) - k5 k6) +

+ Q 4 k ₄ ( 1 + k ₆ ) + Q ⁴ k ₆ - k ₄ k 5 , d ₂ = в ⁴ ( k 5 ( k ₂ + k ₆ ² - k ² ) + k ₂ k ₄ k ₆ ) + + в ² ( 2 k ₄ k 5 ( k ₆ + k ) -Q ⁴ ( k ₂ + k ₆ ² - k ² ) -- Q ⁴ ( k ₂ k ₄ + k ₅ + k ₄ k ₆ + k ₅ k ₆ ) ) + + Q ⁴ ( Q 4 ( 1 + k ₆ ) - k ₅ - k ₄ k ₆ ) + k ₄ Q 4 ( Q h - k 5 ) , d ₃ = - в 6 k ₂ k ₅ k ₆ + в 4 ( - k ₂ k ₄ k ₅ + k ₂ k ₆ Q ⁴ + k ₅ Q hh ( k ₂ + k ₆ ) ) + + в 2 ( Q ⁴ ( k ₂ k ₄ + k ₅ k ₆ - k ₂ Q h ) + + Q 4 ( k 4 k 5 - k 6 Q ⁴ - k 5 Q 4 ) ) + Q ⁴ ( Q h - k 4 )( q 4 - k 5 ) .

В частном случае, когда a = 0, частное решение (6) будет зависеть лишь от координаты y :

W k = AH - ⁽ p о у ); ф^ = 0; ф У Х = H ‘ ⁽ p о у ),

Полагая F = 1 в системе (17), неопределенные коэффициенты (16) находятся в форме

E , (в) =

что приводит к характеристическому уравнению вида k2k5p04 + (k2Q4 + k5Qh) pl + Q4 (Q4 - k5) = 0,   (13)

^kk 4 ^q 2 ^{- k} 5 ( ^q 2 ^{- k} 6^в2 ^{- k} 4 ^+Q h ) q , ( kk ₄ q l ² - kk ₅в 2 + k ₄ k ₅ + kQ⁴ )

корни которого имеют вид

p l ,0

- ( Q ⁴ k ₂ +Q h k ₅ ) ± ^ ( Q ⁴ k ₂ +Q h k ₅ ) ² + 4 k ₂ k ₅ ² Q ⁴

2 k ₂ k ₅

где l = 0 соответствует знаку «+» и l = 1 соответствует

знаку «–».

При этом

k 5 p l ,0

k 5 p lo +Q 4

Аналогичным образом строится часть решения в форме тригонометрического ряда по координате y . Действительно, решение в форме

W / = EH ( qx )T (вy ), ф Х 2 j = FH k ( qx — y ),           (16)

ф У 2 - = GH k ( qx T ' (в y )

приводит после подстановки в систему дифференциальных уравнений (4) к равенствам

'qk 4 E + ( q ² - k б в² - k 4 +Q 4 ) F + q в kG = 0,

< в k ₅ E + q в kF - ( k 6 q ² - k ₂в 2 - k ₅ + Q 4 ) G = 0,   (17)

( k ₄ q ² - k ₅в² + Q ⁴ ) E - qk ₄ F - в k ₅ G = 0.

Определитель системы (17) дает характеристическое уравнение для определения q следующего вида:

G , ( a ) =

^k 42 'll ⁺ ( 'll ^{- k} 6^в2 ^{- k} 4 ^{+ Q} 4 ) ( ^k 4 'll ^{- k} 5^в2 ^{+ Q} 4 ) q , в ( Hk ₄ q , ² - Hk ₅в 2 + k ₄ k ₅ + k ^ Q⁴ )

Аналогично (13)–(15) строится частное решение для случая в = 0.

Как уже было отмечено ранее, константы разделения a и в могут быть выбраны произвольным образом, главное условие данного выбора заключается в полноте тригонометрических рядов по системе функций { T k ^{( a} x } и { Т ^(в у ) } соответственно на границах пластины x = ± а и y = ± b . Например, данные константы

можно выбрать в виде, соответствующем классическим рядам Фурье для четной составляющей:

п a n, k = -

, a

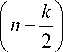
nn a,

п (2 n - 1)

2 a

k = 0, k = 1;

β

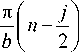
nn b,

п (2 n - 1)

2 b

j = 0, j = 1,

или, наоборот, чтобы нечетная составляющая имела вид классического ряда Фурье:

^a n -1/2, k

п( k + 1)

— I n--I a I 2 J

п (2 n - 1) -4 0- •^k = ⁰

^ n ,       k = 1

I a

^e n -1/2,

П

b

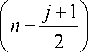
n (2 n - 1)

2 b = < nn

. b ’ j = 0, j = 1.

Очевидно, что для полноты представления решения по системе функций { T _k ( a _n,_k x } и { T (в _n , j y ) } необходимо учитывать для четной составляющей общего решения частные решения, соответствующие a = 0 и P = 0. В то же время для представления по системе { ^Tk ^{( a} n - 1/2 ,k x } и { T j ⁽P n - 1/2, j- У ) } этого делать ^не нужно.

Суммируя построенные частные решения с некоторыми неопределенными коэффициентами X _1n и Y n , получаем общее решение (4) по системе { T _k ( a _n,_k x } и jn.У ) } :

^Wkj = ⁸ k 0 ^{( X} 10 ^A1,0k^Hj ⁽ p 1,0 k y ) + ^X 20 A 2,0 k^Hj ^{( P} 2,0 k y ) ^{) +}

+ 8j0 (Y10E1,0jHk (Q1,0 jx) + Y20E2,0jHk (q2,0jx)) + да 3

+ 22 XinAi,nkHj (Pl,nky)Tk (ankx) + n=1 1=1

да 3

+ 22 Y ln E l , nj H k ( Q l , nj X ) T j ( P n y );          (22)

n =1 1 =1

^ф x , kj = ^ j 0 ⁽ Y 10 ^H j ^{( Q} 1,0 j x ) ⁺ Y 20 ^H j ⁽ q 2,0 j x ) ) ⁺ да 3

+ 22 XnBf, nkHj( Pl,  ) T/(a nkX) + n=1 1=1

да 3

+ 22 Y n H k ( Qi , nj X ) T ( P пУ ),          (23)

n =1 1 =1

фy,kj = 8k0 (X10Hj (p1,0ky) + X20HJ (p2,0ky)) + да 3

+22 XH'i(Pl, nky) T(a nkx)+ n=1 1=1

да 3

+ 22 Y n G l , nj H k ( Q l , nj x )T J ( P nj y ),          (24)

n =1 1 =1

где 8 mn - символ Кронекера.

И по системе функций {Tk (an-1/2,kx} и {Tj(en-1/2,j-y)} да 3

W k = 22 X n A , nk H j ( p l , У)T ( a n -1/2, k X ) + n =1 l =1

да 3

+ 22 Y ln E l , nj H k ( Q 1 , nj x T ( P n - 1/2,j y ),        (25)

n =1 l =1

да3

ф x , kj = 22 X n B, , n_k HA p l , У ) T j ( a n -1/2, k X ) + n =1 l =1

да 3

+ 22 Y n H k ( Q l , n- x ) T ( в n -1/2, j- y ),          (26)

n =1 l =1

да 3

Ф y, kj =22 XlnHJ (P l, nky ) Tk (a n-1/2, kx ) + n=1 l=1

да 3

+ 22 Y n G l , nj H k ( Q l , nj x )T j ( e n -1/2, j- y ),         (27)

n =1 l =1

где P_{l nk} и <7 _{1 nJ} — корни характеристических уравнений (9) и (18), соответствующие константам разделения (21).

• 2.    Решение в случае защемленной пластины

Условия полного защемления сторон пластины x = ±а : W = фx = фy = 0 и y = ±b: W = фx = фy = 0 (28)

можно выполнить, опираясь на любое из представленных выше решений. Однако форма решения (25)-(27) позволяет выполнить четыре условия из (28) точно, в то время как решение (22)-(24) - только два. Действительно, для (25)-(27) можно увидеть, что любого типа симметрии

Tk (an-1/2, ka) = Tj-(pn-1/2,jb) = 0, тогда, если неизвестные коэффициенты

XlnHj(Pl,nkb) = xn и YlnHk((/1,nja) = Ут связаны соотно шениями

Д R 3, nk -°1, nk - A R ^1, nk B3, nk —------- A R A2, nkB 3, nk -A R    1 n, A3, nkB 2, nk x 3 n A R = ^1, nk B2, nk - A2,nkB1,nk x„,             (29) AB ^2., nk 3, nk -AR  1 n 3, nk B2, nk E-, - G, 3, nj 1, nj — E, -G-. -1,nj 3,nj y 2 n E^ - G-. - 2,nj 3,nj _ г        y 1 n, E 3, njG2, nj EG 1, nj 2, nj - E,  G, . 2,nj 1,nj У 3 n E, G. . 2,nj 3,nj — F F   y 1 n, E 3, njG 2, nj формулы (25)-(27) дают

W ( ± a , y ) = W ( x , ± b ) = ф _y ( ± a , y ) = ф _x ( x , ± b ) = 0.

Оставшиеся два краевых условия приводят к двум функциональным уравнениям:

/I \       X-1 D    Hj (Pl,nky) z i\n фx,у(±a,y) = 22xlnBl,nk u(-1) + n=1 l=1           Hj (Pl, nkb)

да 3

+ 22 У1п ^Cth k ( Q l , nj a ) Tj ( P n - 1/2,j y ) = 0,       (30)

n =1 l =1

да 3

ф y , kj ^{( x ,} ± ^b ) = 22 x ln ^Cth j ^{( P}l , nk b^{) T}k ^{( a} n -1/2, k x ) ⁺ n =1 l =1

да3

+ 22 ya , n n =1 l =1

H k ^{( Q l , nj} x ) ( - 1) ⁿ = 0.

H k (<7 1 , nj a )

H ' ( z )

где Cth . ( z ) = —----.

j       H j ( z )

Используя разложение гиперболических функций по тригонометрической системе [30]

H k ( qx ) = ² у ⁽ 1)    ^am -1/2, k^Tk ^(а m -1/2, k x )

H k ⁽ qa )    a m _i          a m -1/2, k + q ²         ’

H j( РУ ) = I у ( — I) m +1 P m -1/2 j T j ( P m -1/2 , У ) h ( рь )   ь ^j       e m - 1/_У + p²

и тождество, возникающее из теоремы Виета для корней характеристических уравнений k5k2(am-1/2,k + q1,nj )(am-1/2,k + q2,nj )(am-1/2,k + q3,nj ) =

_ k4 (вП-1/2j + P12mk )(Pn-1/2j + PXmk )(Pn-1/2j + PXmk ), получаем из равенств (30) бесконечную систему линейных алгебраических уравнений вида

2a c         m-1/2,k x = m Ac

1m to a m-1/2, k

xx

^ n      I n

хУ    .           .       .           .        ..

2     4- n2  YR2     4- n2 YR2     4- n21

^{n _1 ( p} n -1/2 j ⁺ p 1, mk ^{)( p} n -1/2 j ⁺ P 2, mk ^{)( p} n -1/2 j ⁺ P 3, mk )

y^

vc ym

2 P m - 1/2j ------- х

to

P m -1/2 j"

AC

2m yy

^ n      I n

хУ    .           .       .           .       ..

2     4-Л2 W/,2     4-Л2  Y/72     4-Л2 1

n =1 ^{( a}n -1/2, k ⁺ q 1, mj ^{)( a}n -1/2, k ⁺ q 2, mj ^{)( a}n -1/2, k ⁺ q 3, mj )

x C ,

( m = 1,2,_)

где xc

( - 1) m k 2 k 5

AB z, mk 3, mk

-

AB 3, mk 2, mk

^X 1 m ^,

y^c m

( - 1) m k 4

E, G- .

2, mj 3, mj

-

E 3, mj G 2

t y 1 m ^, 2, mj

Ex = G, E„ G. Aqk2 - -q2 ) + С, -E, G, Aq2 .-q2 ) + n        1,nj 2,nj 3,nj Vq 3,nj    q1,nj A       1,nj 3,nj 2,n/Vq 1,nj     q 2,nj 7

+ G 2, nj E 1, nj G 3, nj ( q 2 nj - q 3, nj ),

П X = G 1, nj E 2, A ,j< ^ X nj (q 3, nj - q nj ) + G 1, nj E 3, nj G 2, nj q k, nj X

X (q12 nj - q2, nj)+G 2, njE1, njG3, njq1, nj (q22, nj - q2, nj), ey=B. л в, Ap2. -p2 л + в. -4 в, Ap21 -p2 J + n 1,nj 21_nnj 3,njVr 3,nk    p1,nk /      1,nj 3,nj 2,njVr 1,nk    p 2,nk A

+                    — py /

2, nj 1, nj 3, nj vr 2, nk     p 3, nk

П У = B 1, nj A 2, nj B 3, nj P 2², nk ( P 3², nk - P 2nk ) + B 1, nj- A 3, nj B 2, njP3,nk X

^{X (} p 1, nk - p 2, nk ) ^{+ B} 2, nj ^A 1, nj^B 3, nj^p1,nk ⁽ p 2, nk - p 3, nk ),

A C /а = (Л ,-A. jeth fp, +

1 m        \ ^, mk 3, mk     3, mk 2, mk )     jX^p\, nk A

^{+ ( A} 3, mk^B1,mk - ^A 1, mk^B 3, mk ) Cth j ( p 2, nk b ) +

^{+ ( A} 1, mk^B 2, mk    A - 2, mk^B1, mk ) Cth j ( P 3, nk b ),

A C !Ь = 2е, G. --E-      )cth.( q, a) +

2 m         \ 2, mj 3, mj 3, mj 2, mj J      kvq1,nj A

+ {e,                          a) +

\ 3, mj 1, mj      1, mj 3, mj J kvq 2, nj A

+ {e, G, --E, Лаь,(4 aY

\ 1, mj 2, mj       2, mj 1, mj J      kvq 3, nj A

• 3.    Решение в случае свободных краев пластины

Как известно, в случае полностью свободных краев толстой пластины краевые условия принимают следующий вид:

x = ± a : M_x = M xy = Q x = 0

и                                                      (32)

y = ± b : M y = M xy = Q y = 0.

Вычисляя по формулам (2) силовые характеристики пластины на основе общего решения (22)-(24), можно получить

• - MD j = k *5 k о ( X 10 P 1,o k^Hj ⁽ P 1,o k y ) ⁺ X 20 P 2,0 k^Hj ⁽ P 2,0 k y ) ) ⁺

• ^{+ 5} j 0 ⁽ 1 ^0 ^q 1,0 j^Hk ^{( q} 1,0 j x ) ⁺ Y 20 q 1,0 j^Hk ⁽ q 2,0 j x ) ) ⁺

⁺ ЁЕ ^Xm ( ^k * Pl , nk ^-a nk^Bl , nk ) ^Hj ⁽ Pl , nk y ) T k ^{( a} nk x ) ⁺ n =1 l =1

+j^]E Y n ( q i , nj - k * P nj G i , nj ) H k ( q i , nj x ) T j ( P nj y );   (33)

n =1 l =1

D“— — k 2 ⁵ k 0 ^{( X} 10 ^P 1,0 k^Hj ^{( P} 1,0 k y ) ^{+ X} 20 ^P 2,0 k^Hj ^{( P} 2,0 k y ^{) ) +}

^{+ 5} j 0 ^{k (} Y 10 q 1,0 j^Hk ⁽ q 1,0 j x ) ^{+ Y} 20 q 1,0 j^Hk ⁽ q 2,0 j x ) ) ⁺

⁺ SS ^Xln ( ^k 2 P l , nk - ^k ‘^a nk^Bl , nk ) ^Hj ⁽ P l , nk y ^{) T}k ^{( a} nk x ) ⁺ n =1 l =1

+ ]Y]E Y n ( k * q l , nj - k 2 P nj G l , nj ) H k ( q l , nj x ) T j ( P nj y ); (34) n =1 l =1

- M xy ^{, k L} = k 6 :Ё]Е X ln ( a nk + P l , nk B l , nk ) H ‘ ( P l , nkY ) X D 1           n =1 l = 1

X T k ( a n_k x ) + k 6 jT jH Y n ( p nj + q l , nj G l , nj ) x

X H k ( q l , nj x ) T j ( P nj y );                   (35)

QD kj = k 4 5 j 0 ( 1 10 ( q 1,0j E 1,0j - 1 ) H k ( q 1,0 j x ) +

^{+ Y} 20 ( q 2,0 j^E 2,0 j ^- 1 ) ^H k ⁽ q 2,0 j x ) ) ⁺

+ ^k4 ЁЕ X ln ( a nk A l , nk - B l , nk ) H j ( Pl , nk y )T ‘ ( a nk x ) + n =1 l =1

+ k 4 ]Y]E Y n ( q l , nj E l , nj - 1 ) H k ( q, , nj x ) T j ( p ^ y );    (36)

n =1 l =1

QD j = k 5 5 k 0 ( X 10 ( P 1,0 k A 1,0 k - 1 ) H j .( P 1,0 k y ) +

+X20 (P2,0kA2,0k !)Hk ( P 2,0 ky)) + co    3

+ ^k 5 EE X in ( Pi , nk A l , nk ^- 1 ) H j (P l , nk y T ^{( a} nk x ) + n =1 l =1

co 3

+ k 5 EE Y ln ( в nj E l , nj - G l , nj ) H k ( qi,nj X ) T /( P n y ),   (37)

n =1 l =1

где k * = k - k ₆..

Учитывая, что для используемой тригонометрической системы функций верно тождество

Tk(« n, ka) = Tj(e n j) = 0, можно увидеть, что из шести краевых условий (32) четыре условия выполняются точно, если неизвестные коэффициенты связаны соотношениями

Y 0 H k ( q j ) = - Y 20 H k ( q 2,o j a ) = -kq j^ ay OF , (38) ^k 4 ⁽ q 1,0 j q 2,0 j )

X 10 H ' ( P 1,0 k b ) = - X 20 H j (p 2,0 k b ) =   k ^{5 P} 2^{1,0 k  П}   bx F , (39)

^k 5 ( P 1,0 k ^- P 2,0 k )

YH ( q l , nj a ) = a ( — 1) n ^{+ j} T n 1 Z ,           (40)

—

n »  3

> EE

A 2 m n =1 l =1

^Pl , nk ( k ^Pl , nk   « nk

P m, - ^{+ P} 2 nk

b,„ a „ xF, (m = 1,2,_),   (42)

где ^Th . ( = ) = HyZ). , ^H k ^{( z} )

kb

Al0 =---TA—2— x k5(P10 k - P20 k )

^X ( P 10 k ( k 5 P w k ^{+ Q4} ) Th j K k ^b ) ^-

^- P 00k ( k 5 P 220 k ^{+ Q4} ) Th j (P 20 k ^b ),

^A20 =, ₍ 2      2 x( q 10 j ⁽ k 4 q 10 j ⁺ ^ ) ^Th k ⁽ q 10 j a )

k 4⁽ q™ j ^- q 20 j г

• ^- q 20 j ^{( k} 4 q 20 j ⁺ ^ ) ^Th k ⁽ q 20 j a ) ) ,

ЛF =bV(k„р, ,—к*а .B, ,)S ,,Th kbY 1 m              2 Pl, mk         mk l, mk ) m 11 j ^l, mk 7, l=1

A F =аУ--к‘й _tG, )T        a\

• 2 m       / j \ q l , mj       mmk^l , mj / m 1 1 k^ q l , mj .

l =1

X ln H j ( P l , nk b ) = b ( - 1) ^{n + k} S n 1 X ( l = 1,2,3; n = 1,2,...), (41)

где T n 1 ₁ и S _n 1 ₁ - алгебраические дополнения к элементам (1, l ) матриц

<7. E. - -1 q„ -E, - -1 q. E, - -1 q 1, nj 1, nj               q 2, nj 2, nj               q 3, nj 3, nj

^H nj q 1, nj ^1, nj     nuj q 2, nj   2,nj n^nj q 3, nj ^3,nj J

P 1, nk A 1,nk ^{- 1}       P 2, nk A 2 , nk ^{- 1}       P 3, nk A 3, nk

. « nk ^{+ P} 1, nk ^B 1,nk   « nk ^{+ P} 2, nk ^B 2, nk   « nk ^{+ P} 3, nk ^B 3, nk у

Оставшиеся два краевых условия на моменты M x и M y выполняются из решения бесконечной системы относительно неизвестных x F , y F :

F u k 0 x 0

5 j 0 у F

5 k 0 k a

5 k

"   A F

o

5 j 0 y F + EE 1 -

k 2 ₽ nj G l

co 3 I

5 k 0 xF + EE | 1 -

k * ql, nj a , B, , nk   l,nk

y _n

к * n I n k Pl, nk J

x m ^F

2 5 j ₀ k ^a mk ( ^k 4 ( ^q 10 j ⁺ q 20 j ) ⁺ "  ) ⁺ k 4 ^q 10 j q 20 j  F

Ck 4         ( « mk + qFj^ ( ^a mk ⁺ q 2²0 j )        у ⁰

^F y _m

2_ у у q l , nz ( k ‘ q l , nj ^- k 2 ^в nj G l , nj ) F

A ^F                  ГУ ² 4- Л ²           n, ’

A 1 m n =1 ^l =1           « mk ⁺ q l , nj

2 5 k ₀ k ^в mj ( k 5 ^{( P} 10 k ^{+ P} 20 k ^{) +} ^ ) ⁺ k 5 ^P 10 k ^P 20 k

^ Fm k 5          ( ^e mj ⁺ P 20 k )( p mj ⁺ P 220 k )

4. Численные результаты

Нетривиальные решения однородных бесконечных систем линейных алгебраических уравнений (31) и (42) позволяют выполнить условия полного защемления (28) и свободных краев пластины (32). Наиболее часто используемым методом для отыскания приближенного решения и собственных частот является метод редукции, когда в бесконечной системе удерживают первые N уравнений и неизвестных, отбрасывая остальные. При этом определитель редуцированной системы служит дисперсионным уравнением для определения собственных частот.

В табл. 1 представлена сходимость метода при отыскании собственной частоты для удлиненной толстой изотропной пластины в случае свободных краев. Можно заметить, что удержание в расчетах N = 16 первых слагаемых в представлении решения (22)-(24) позволяет достичь сходимости метода. При этом полученные результаты находятся в отличном соответствии с известными в литературе [18] значениями собственных частот. Аналогичная картина наблюдается и для других комбинаций параметров задачи, в том числе и для ортотропного материала.

Заметим, что согласно представленному подходу уравнения свободных колебаний (3) выполняются по построению. Качество полученного приближенного решения определяется точностью выполнения однородных граничных условий. При этом из трех граничных условий на каждой из сторон пластины два условия оказываются выполненными по построению. В частности, для защемленной пластины на сторонах x = ± a форма решения (25)-(27), такова, что W = ф _y = 0, а на

сторонах y = ± b получаем W = φ _x = 0. Аналогично для пластины со свободными краями: на сторонах x = ± a форма решения (22)-(24) приводит к тому, что M_xy = Q_x = 0, на сторонах y = ± b получаем M_xy = Q_y = 0. Таким образом, на каждой стороне пластины выполняется лишь по одному краевому условию из решения бесконечной системы, соответственно, в угловой точке будут выполнены точно все краевые условия, кроме двух условий, выполнение которых обеспечивает решение соответствующей бесконечной системы. В табл. 2 представлено выполнение однородных краевых условий для пластины со свободными краями M x ( a , y ) = 0 при увеличении порядка редуцированной системы N (для второго условия M y ( x , b ) = 0 - ситуация схожая). Можно увидеть, что с увеличением N качество выполнения однородных условий улучшается, в том числе и в угловой точке. Конечно, точно выполнить условие в угловой точке без исследования асимптотики неизвестных в бесконечной системе не представляется возможным, тем не менее численный анализ показывает, что все поставленные краевые условия выполняются с удовлетворительной точностью.

Таблица 1

Сходимость метода редукции при отыскании собственных частот толстой пластины v = 0,333,к = 0,8601, hIa = 0,1, bIa = 3 со свободными краями

Table 1

Convergence of the reduction method for the fundamental natural frequency of a rectangular completely free isotropic

Mindlin plate with v = 0,333, к = 0,8601, h I a = 0,1, b I a = 3

Метод	Q j
	1	2	3	4	5
N = 4	0,7673	1,0252	1,2781	1,4904	1,8021
N = 8	0,7670	1,0248	1,2778	1,4902	1,7910
N = 16	0,7670	1,0248	1,2776	1,4902	1,7909
[18]	0,7657	1,0140	1,2715	1,4715	1,7741

Таблица 2

Сходимость в выполнении однородных краевых условий для первой собственной частоты Q = 0,7657

при v = 0,333, к = 0,8601, h I a = 0,1, b I a = 3

Table 2

Convergence test of fulfilling FFFF boundary conditions for first natural frequency Q = 0,7657 with v = 0,333, к = 0,8601, h I a = 0,1, b I a = 3

y	M x	( a , y ) /Mmax
b	N = 8	N = 16	N = 32
0,0	0,0457	0,0028	0,0003
0,2	–0,0217	0,0004	–0,0002
0,4	0,0119	–0,0006	0,0001
0,6	–0,0894	–0,0015	–0,0005
0,8	–0,1119	0,0112	–0,0008
1,0	0,1243	–0,0226	–0,0012

В табл. 3 представлена сходимость метода для пластины с защемленными краями в сравнении с результатами [22]. Так же как и для пластины со свободными краями, удержание в бесконечной системе первых N = 8 уравнений и неизвестных позволяет получить удовлетворительную точность решения. Полученные решения практически совпадают с данными [22].

Таблица 3

Сходимость метода редукции при отыскании собственных частот толстой квадратной пластины v = 0,3, к = 5/6, h I a = 0,1 с защемленными краями

Table 3

Convergence of the reduction method for the fundamental natural frequency of a square clamped isotropic Mindlin plate with v = 0,3, к = 5/6, h I a = 0,1

Метод	Q j
	1	2	3	4	5
N = 4	0,9086	1,2546	1,2546	1,4850	1,6112
N = 8	0,9084	1,2543	1,2543	1,4847	1,6109
N = 16	0,9083	1,2542	1,2542	1,4847	1,6108
[22]	0,9077	1,2537	1,2537	1,4843	1,6108

Разработанный в статье подход дает возможность построить собственные формы колебаний пластины. На рис. 2 представлены собственные формы толстой квадратной пластины h I a = 0,1 со следующими параметрами: к = 0,8601, E 1 = 60,7 ГПа, G 12 = G ₁₃ = G ₂₃ = 12 ГПа, v ₁₂ = 0,23, v ₂₁ = 0,094 в случае защемленных и свободных краев пластины.

Заключение

Полученные асимптотические точные решения задач теории упругости для колебаний толстых пластин имеют самостоятельное теоретическое значение, так как впервые удается получить эффективное аналитическое решение поставленных задач. Практическое значение представленных задач состоит в том, что высокочастотные колебания перечисленных выше объектов встречаются в различных прикладных задачах технического характера. В частности, пластинки прямоугольной формы представляют особый интерес в микро- и наноэлектронике, в задачах строительной механики, при моделировании технических систем, в геофизике и др. Данные решения могут быть использованы для параметрической оптимизации, анализа устойчивости к вибрации технических систем.

В частности, данные решения могут служить основой для развития Dynamic Stiffness Method применительно к ансамблям толстых ортотропных пластин и найти свое коммерческое применение при разработке программных комплексов на основе DSM для моделирования сложных технических систем в таких отраслях, как судостроение, авиастроение, автомобилестроение.

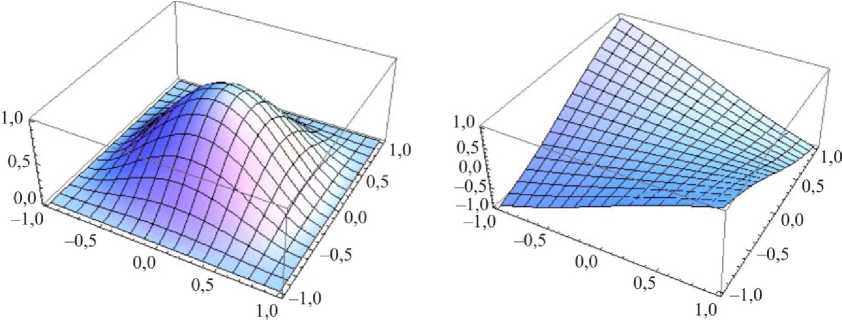
fi С = 2,6527

fi f = 1,5643

а                                                б

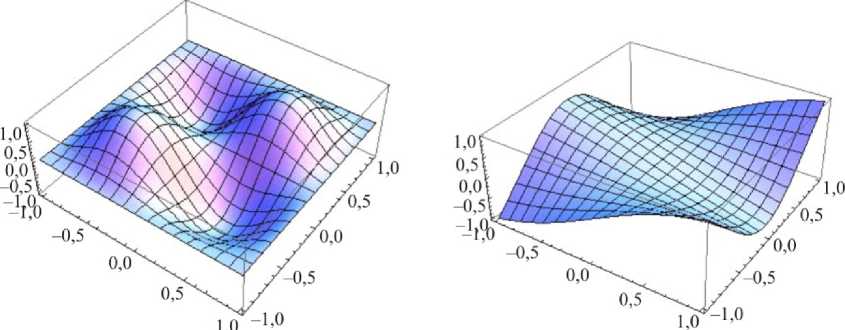
fi 4 = 4,4539                                   fi F = 2,4490

в

г

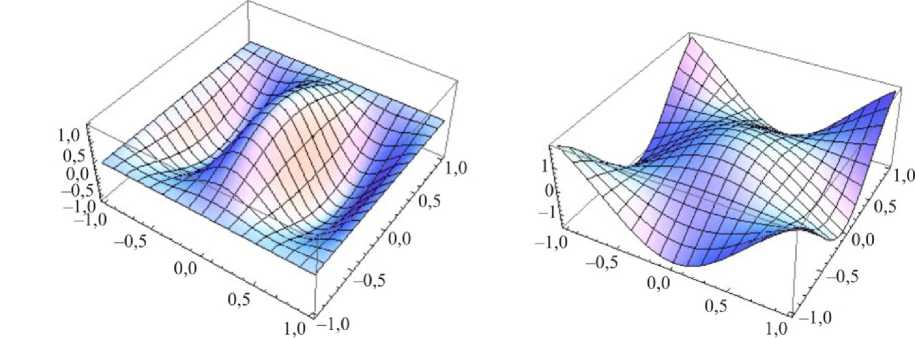
fi C = 5,3035

fi f = 3,4095

д

е

Рис. 2. Собственные формы колебаний толстой ортотропной пластины: а , в , д – полностью защемленная пластина; б , г , е – пластина со свободными краями

Fig. 2. The natural modes of a thick orthotropic plate: a , c , e – fully clamped plate; b , d , f – completely free plate

Исследование выполнено при финансовой поддержке РФФИ и города Севастополя в рамках научного проекта № 18-41-920001\18.