Новые двусторонние оценки полных эллиптических интегралов первого и второго рода
Автор: Алексеева Е.С., Рассадин А.Э.
Журнал: Огарёв-online @ogarev-online
Статья в выпуске: 12 т.9, 2021 года.
Бесплатный доступ
В работе доказаны две теоремы, в которых установлены оценки снизу и сверху для полных эллиптических интегралов первого и второго рода, выражающиеся через элементарные функции. Эти теоремы применены к модельному геометрическому примеру. Кроме того, в статье представлены графики зависимостей от модуля этих интегралов как полученных оценок, так и их относительных погрешностей. Применимость найденных аппроксимаций для технических приложений также обсуждена.
Гипергеометрическая функция, инженерная точность, круговой цилиндр, неравенство гёльдера, объём
Короткий адрес: https://sciup.org/147249997
IDR: 147249997 | УДК: 517.583,
Текст научной статьи Новые двусторонние оценки полных эллиптических интегралов первого и второго рода
Необходимость в вычислении значений полных эллиптических интегралов первого:
П 2
К (k) = J '.(1)
о 1 - - k 2 sin2 '
и второго рода:
E(k) = J 71 - k2sin2' • d'(2)
о часто возникает в самых разнообразных задачах (см., например, [1, 2]).
При фиксированном k e (0,1) существует целый ряд алгоритмов для определения величин интегралов (1) и (2). Например, полный эллиптический интеграл первого рода можно вычислять методом арифметико-геометрического среднего, который предложил ещё К.Ф. Гаусс [3, с. 160], а полный эллиптический интеграл второго рода можно найти способом, описанным в [4]. Однако для теоретического исследований выражений, содержащих функции (1) и (2), эти методы неудобны. Более эффективными в такой ситуации являются двусторонние оценки интегралов (1) и (2). Примеры таких оценок дают следующие теоремы.
Теорема 1. При k е [0,1] полный эллиптический интеграл второго рода удовлетворяет неравенствам:
где
и
Е - ( к ) <Е ( k ) <Е + ( k ) ,
ππ
Е ( к ) =----
2 2
1 - (1 - к 2у
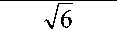
Е + ( к ) = П . J1 -
4 ■ к2
Доказательство. При к е [0,1) производная от функции (2) по модулю к имеет вид:
d Е ( к ) П 2 sin2 ф ■ d ^
= - k ⋅ ∫ .
dк о д/1 - к 2 sin2 ф
Представим подинтегральное выражение в правой части формулы (6) как произведение двух функций: f (ф) = sin2 ф и g(ф) = (1 - к2 sin2 ф) 1/2, и применим к этому интегралу как прямое, так и обратное неравенство Гёльдера [5, с. 11].
Сначала выберем следующие значения показателей Гёльдера: p = q = 2 , тогда прямое неравенство Гёльдера есть не что иное, как неравенство Коши-Буняковского, а равенство (6) при к е (0,1) даёт:
1 dE(к) П2 sin2 ф. dф П2 . 4 П2
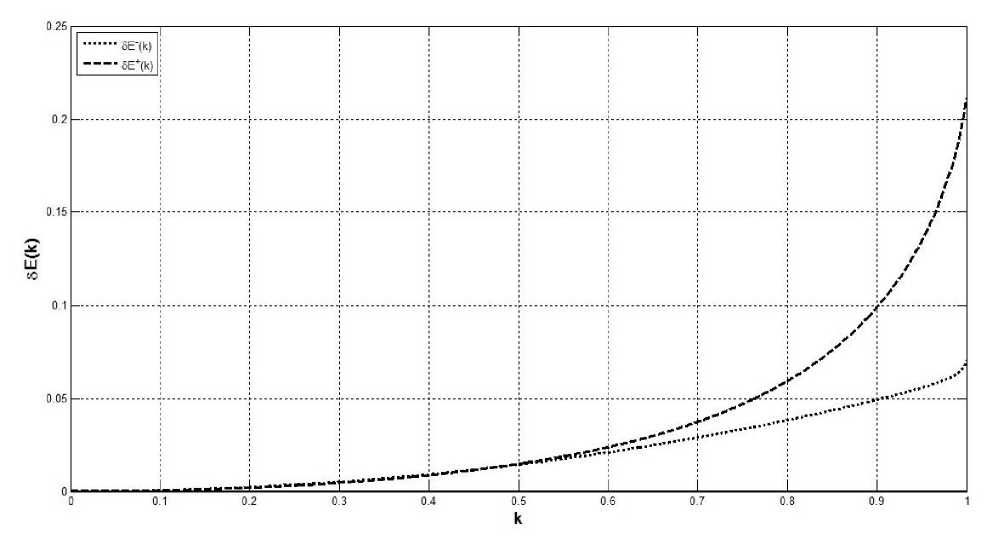
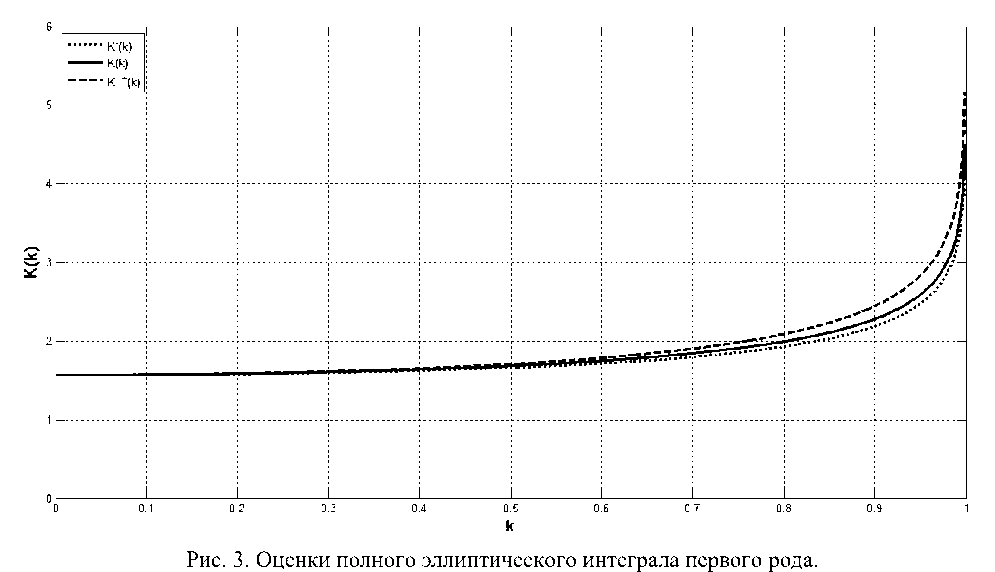
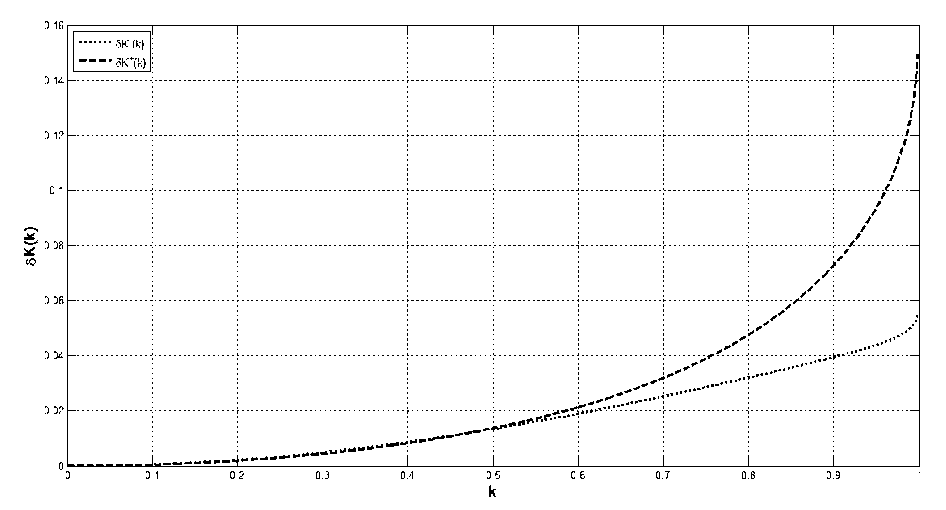
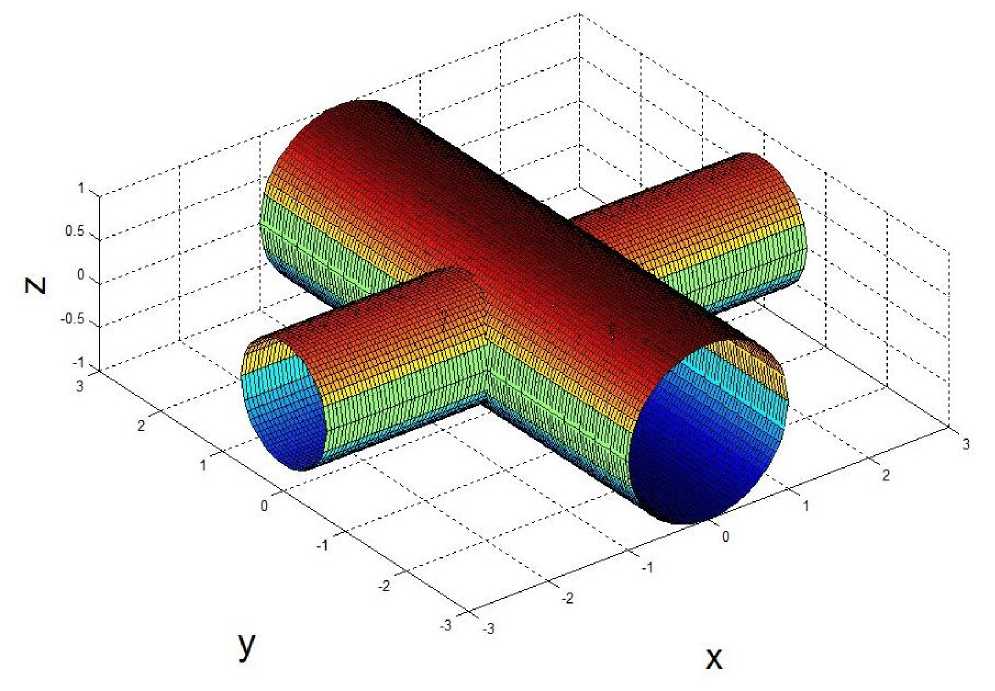
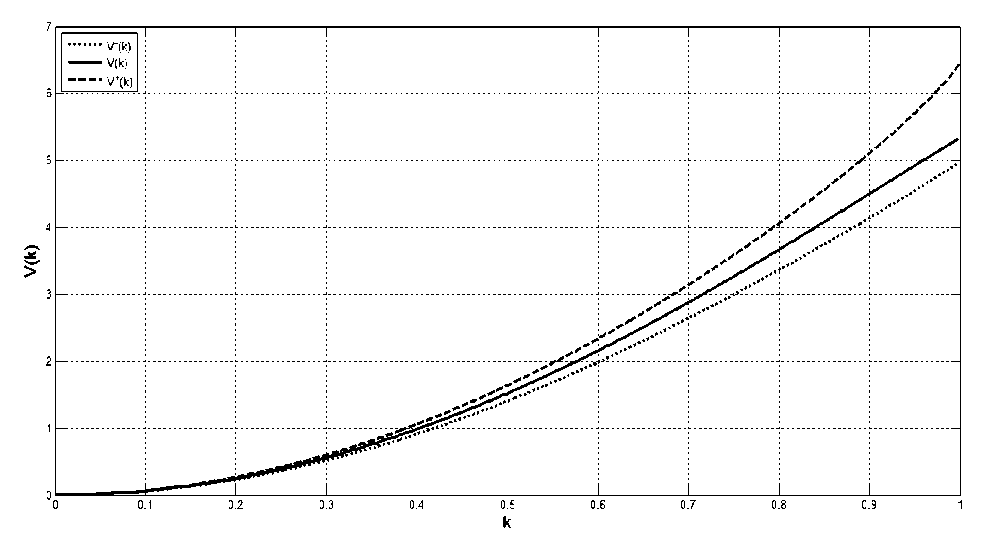
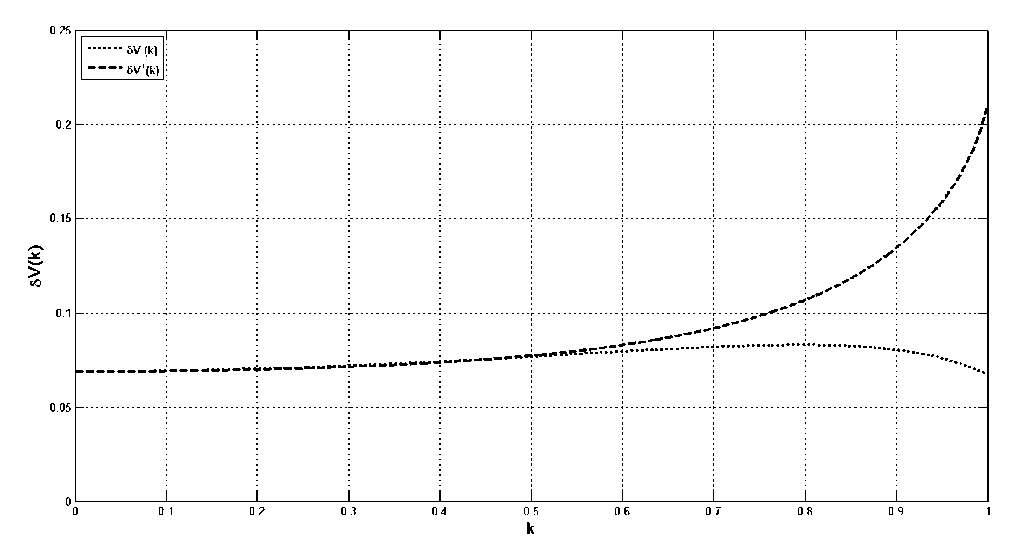
--— = I = к ак J0 1 - к2 sin2ф V о V о 1 - к sin ф Интегралы в правой части этого неравенства вычисляются элементарно. Таким образом, неравенство (7) сводится к следующей оценке для производной от функции (2): dE(к) <п Гз к е (0,1) . ак “4 \ 2 ' ,\ к, Интегрируя неравенство (8) по модулю эллиптического интеграла от 0 до к, используя свойства интеграла Римана и учитывая, что Е(0) = П2 , получим, что при к е (0,1) Е (к) < Е(к) с функцией (4) в левой части этого неравенства. Справедливость неравенства при к = 0 и к = 1 проверяется непосредственно. Далее, применим к выражению (6) обратное неравенство Гёльдера [5, с. 16] с показателями Гёльдера p = 1/2 (для функции f (p)) и q = -1 (для функции g (p)): 1 dE(k) _П2 sin2p ■ dp > k dk0 1 - k2 sin2p П 2 П 2 j(sin2p)12dp ■ J 71 - k2 sin2p ■ dp 0 0 Неравенство (9) даёт для производной функции (2) следующую оценку: dE(k) > k dk ’Ek ’ k e (0,1). Обращаясь с неравенством (10) так же, как и в предыдущем случае, для k e (0,1) получим неравенство E(k) Теорема 1 иллюстрируется рис. 1, на котором представлены графики двусторонней оценки (3). Они демонстрируют, что при k e (0,1) функции (4) и (5) приближают функцию (2) весьма неплохо. Рис. 1. Оценки полного эллиптического интеграла второго рода. Для того, чтобы выразить количественно, насколько хорошо приближают полный эллиптический интеграл второго рода его оценки снизу (4) и сверху (5), введём относительные погрешности: 3E ( k ) = E( k ) -E-( k ) E( k ) Ж+ (k) = E+( k ) -E( k ) E( k ) Графики функций (11) в зависимости от модуля k полного эллиптического интеграла приведены на рис. 2. Из этого рисунка видно, что Ж-(k) < 0,05 при k е[0, 0,9], а Ж+(k) < 0,05 при k е [0, 0,76], следовательно, при k е[0, 0,76] функции (4) и (5) можно применять при решении прикладных задач для оценки полного эллиптического интеграла второго рода с инженерной точностью. Рис. 2. Относительная погрешность оценок полного эллиптического интеграла второго рода. Аналогичная теорема может быть доказана и для функции (1). Теорема 2. При k е [0,1) полный эллиптический интеграл первого рода удовлетворяет неравенствам: К-(k) <К(k) <К+(k),(12) где 3 К-(k) = - - П •1 ~(1 -k )4 - П-|1 |-ln(1 - k2)(13) 26 Тб 4 ^ Тб) и п п Г 4 п L 4" , J1 -4k21п2 + J1 - 4/ п2 К+ (k) = -- • 1--у ln(1 - k2) + -• 1--у In^-------' '---.(14) 2 4 V п2 2 V п2 1 + 4 - 4/ п2 Доказательство. В работе [6] выведена следующая нелокальная связь между функциями (1) и (2), справедливая при k е [0,1): К (k) = Е( k) + Г q 'Е(q)' dq 0 1- q . Комбинируя соотношение (15) с двусторонней оценкой (3) с функциями (4) и (5) и выполняя элементарное интегрирование, придём к двусторонней оценке (12) с функциями (13) и (14). Теорема доказана. На рис. 3, который иллюстрирует утверждение теоремы 2, приведены графики двусторонней оценки (12). Из этого рисунка видно, что при к е [0,1) функции (13) и (14) приближают функцию (1) довольно хорошо. Для того, чтобы выразить количественно, насколько хорошо приближают полный эллиптический интеграл первого рода его оценки снизу (13) и сверху (14), введём относительные погрешности: - К ( к ) -К-( к ) дК (к) =--------------, К ( к ) ж. ( к ) = К+(к )-К( к ) К ( к) . Графики зависимостей функций (16) от модуля k полного эллиптического интеграла приведены на рис. 4. По нему можно заметить, что дК (к) < 0,05 при к е [0, 0,99], а дК+(к) < 0,05 при к е [0, 0,81], значит, при к е [0, 0,81] функции (13) и (14) можно применять при решении прикладных задач для оценки полного эллиптического интеграла первого рода с инженерной точностью. Рис. 4. Относительная погрешность оценок полного эллиптического интеграла первого рода. Продемонстрируем применение доказанных теорем на следующем примере. Рассмотрим два круговых цилиндра радиусов 1 и k ( 0 < k< 1 ), оси которых пересекаются под прямым углом (см. рис. 5). Рис. 5. Круговые цилиндры разных радиусов с осями, пересекающимися под прямым углом. Объём тела, ограниченного ими, равен [7, с. 214]: V(k) = - • [(1 + к2) • Е(к) - (1 - к2) • К(к)].(17) Комбинируя неравенства (3) и (12), для величины (17) легко получить следующую двустороннюю оценку: V- (к) < V(к) < V+(к),(18) где V-(к) = - • [(1 + к2) • Е-(к) - (1 - к2) • К+(к)](19) и V+(к) = - • [(1 + к2) • Е+ (к) - (1 - к2) • К-(к)].(20) Графики функций (17), (19) и (20) в зависимости от модуля k полного эллиптического интеграла приведены на рис. 6. Рис. 6. Оценки объёма пересечения двух круговых цилиндров разных радиусов с осями, пересекающимися под прямым углом. Для количественной характеризации качества приближения объёма (17) величинами (19) и (20), построенными с помощью функций (4), (5), (13), (14), как и ранее, введём относительные погрешности: 3V - (к) = V(к) - V- (к), V ( к ) .V+ (к) = V + ( к) - V(к > V ( к ) Графики зависимостей функций (21) от модуля k полного эллиптического интеграла приведены на рис. 7. Рис. 7. Относительная погрешность оценок объёма пересечения двух круговых цилиндров разных радиусов с осями, пересекающимися под прямым углом. Из этого графика видно, что SV± (к) > 0,05 при всех к е (0,1), при этом кривая SV+(к) уходит вверх до заметных значений. Однако кривая SV (к) остаётся ограниченной и снизу, и сверху: 0,068 < SV (к) < 0,084 , следовательно, формула (19) вполне пригодна для определения по заданному k значения объёма (17) с инженерной точностью. Таким образом, теоремы 1 и 2, доказанные в этой работе, применимы для оценки величин как полных эллиптических интегралов первого и второго рода, так и их линейных комбинаций, с инженерной точностью. В заключение отметим следующее обстоятельство: как хорошо известно, полные эллиптические интегралы первого и второго рода выражаются через гипергеометрические функции [3, c. 151]: Е(к) = - • F| - 1,1,1, к2 2 ^ 2,2, , К(к) = -• FI -,-,1,к2I, (22) следовательно, утверждения теорем 1 и 2 означают, что специальные функции (22), являющиеся решениями линейных дифференциальных уравнений второго порядка с переменными коэффициентами, могут быть эффективно приближены с помощью элементарных функций.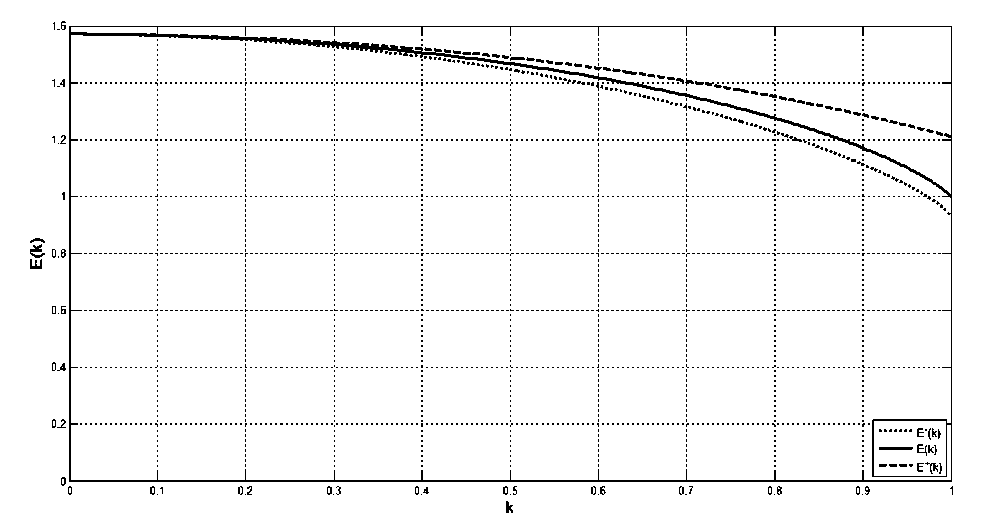
Список литературы Новые двусторонние оценки полных эллиптических интегралов первого и второго рода
- Карпухин М. А. Немаксимальность экстремальных метрик на торе и бутылке Клейна // Математический сборник. - 2013. - Т. 204, № 2. - С. 31-48. EDN: RXPTGJ
- Rassadin A. E., Agalarov A. M.-Z. The modified Whitham modulation theory for transmission line with ferroelectric capacitors // Ferroelectrics. - 2021. - vol. 576, No. 1. - pp. 40-49. EDN: UFREWK
- Ахиезер Н. И. Элементы теории эллиптических функций. - М.: Наука, 1970. - 304 с.
- Алексеева Е. С., Рассадин А. Э. Новый метод вычисления полного эллиптического интеграла второго рода // Алгебра, теория чисел и дискретная геометрия: современные проблемы, приложения и проблемы истории: Материалы XVIII Международной конференции, посвящённой столетию со дня рождения профессоров Б. М. Бредихина, В. И. Нечаева и С. Б. Стечкина. - Тула: Тул. гос. пед. ун-т им. Л. Н. Толстого, 2020. С. 249-251. EDN: VKTBEX
- Соболев С. Л. Некоторые применения функционального анализа в математической физике. - М.: Наука, 1988. - 336 с.
- Алексеева Е. С. Двусторонняя оценка полного эллиптического интеграла первого рода // Международный научно-практический журнал "Глобальная наука и инновация 2020: Центральная Азия". Серия "Физико-математические науки". - 2020. - № 5 (10). - С. 63-66.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. Том II. - М.: Наука, 1966. - 800 с.


