Новые подходы к теории риска

сельском хозяйстве, предложена следующая математическая концепция риска. Состояние системы Человек-Машина-Среда (ЧМС) рассматривается как свойство свободного изменения ее производственных факторов, вызванного любыми причинами [1,2,3]. Изменения могут быть представлены в нелинейном виде:

dy

— = Fi ( у 1 , у ₂,..., У п ), i = 1,2,..., n (1) dt

Примем за безопасное состояние некоторый установившийся процесс работы системы, описываемый функцией y_i ^x ( t ) . Отклонения от этого состояния и переход в опасное представим изменениями y_i ( t ) (рис. 1). Отклонения, определяемые уравнением 1 при определенных начальных условиях y_i ( t_o ) обозначим через y_i ( t ) :

x i ( t ) = y i ( t ) - y x ( t ), i = 1 , 2 , ... , n ,   (2)

тогда можно написать уравнение возможного изменения в отклонениях в виде:

dx

— =Ф , ( x 1 , X 2

,...,

, X n ), i = 1,2,..., n ,        (3)

при этом состояние системы, соответствующее безопасному, будет при

x_i ( t ) =0. Переменные

факторы   Xi (x1, x 2,..., xn), i = 1,2,..., n являются координатами состояния системы в отклонениях.

В общем случае конкретный вид уравнений (3) зависит от вида процесса y_i ( t ) , так как эти уравнения получаются из 1 подстановкой 2.

Состояние системы при X_i ^x ( t ) = 0 называется

безопасным, если приняв "трубку" сколь угодно малого n-мерного сечения ε (рис.2), система в

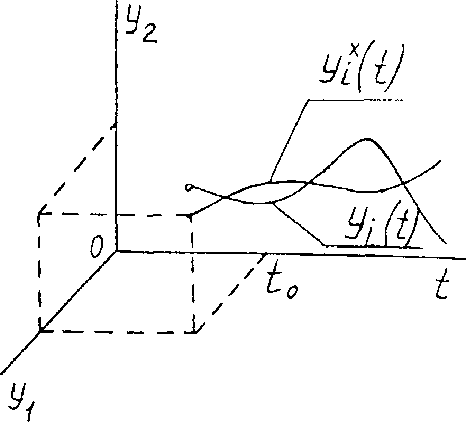
Рис. 1. Изменения параметров системы : Y ^x (t) - функция безопасного состояния системы, Y_i(t) - функция опасного состояния системы.

начальный момент t _о принимает область начальных

условий õ , зависящую от

ε

, что с увеличением

t

функция отклонений X_i(t) не выйдет из заданной "трубки" ε . Математическое понятия безопасности формулируется следующим образом: состояние

системы при X _i^x ( t ) =0 называется безопасным, если

при заданном (нормированном) ε > 0 сколько бы оно мало ни было, существует еще более малое õ>0 ,

зависящее от

ε

, что при начальных условиях:

| X i (t o ) | <  õ, i= 1,2, ..., n,              (4)

в дальнейшем изменении to < t < ∞ выполняется условие безопасности:

| X i (t no ) | <  ε , i= 1,2 ..., n, (5)

Геометрически это означает, что все решения,

которые при t = t о начинаются в õ - окрестности точки

Геометрически безопасное состояние системы n-го порядка можно представить условно в виде некоторой интегральной кривой в n-мерном пространстве с добавленной осью времени t (рис. 1.) Опасное состояние y_i(t ), вызванное начальным отклонением при t=t _о , изобразится другой интегральной кривой y_i^x ( t ) . В качестве начального отклонения могут быть конструктивные несовершенства рабочих мест, машин и технологий, выраженные через отклонения факторов (параметров).

В отклонениях Xi(t) , т.е. в пространстве координат, опасное состояния системы будет выглядеть так, как показано на рисунке 2.

(X₁₀, ..., X_n) никогда не покинут ε трубку решения

Х i (t) (рис.2).

Состояние системы будет опасным, если указанное условие не выполняется, хотя бы для одного отклонения Xi . Если условия, указанные в 4,5 выполнимы и имеем Xi ^{( t )} → 0 при t → ∞ , то безопасность системы при X _i ^x = 0 будет устойчивой. Если же Xi ^{( n )} → 0 при t → ∞ после любых начальных отклонений, то система будет безопасной всегда (абсолютно безопасной). Однако это не означает, что будут безопасны и все процессы в системе, так как свойства составляющих системы

меняются с изменением времени. Примером может

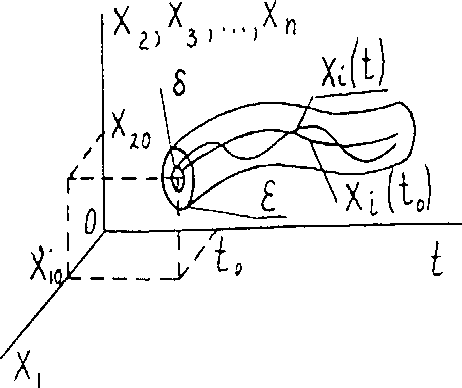
Рис. 2. Изменения параметров системы в отклонениях:

служить наличие в системе уравнений второго порядка, неустойчивых предельных нормированных значений. В этом случае состояние системы оказывается опасной при больших начальных

отклонениях, выходящих за границу

ε

т.е. система

безопасна в "малом" и опасна в "большом".

Проведенные теоретические исследования

позволяют выявить следующее состояние системы ЧМС и предложить классы опасности.

1. Класс 1. Система абсолютно безопасна, когда

параметры системы не превышают опасных

(вредных) уровней, все решения X _i^x ( t ) не выходят

X_i(t_o) - функция отклонений в начальный момент времени,

X i (t) - функция отклонений параметра при увеличении времени,

ε , õ - условия безопасного состояния системы.

Если X _i ^x ( t ) = 0 , то функция X _i^x ( t ) изобразится прямой линией и совпадет с осью t .

из "трубки" õ (ПДК, ПДУ, система технически исправна). Вероятность появления опасности равна 0.

2. Класс 2. Система условно безопасна, когда параметры системы выходят из "трубки" õ , но не

покидают "трубку"

ε

. Появляется риск в работе.

Вероятность становится больше ноля, но меньше 0,5. Параметры системы в отклонениях становятся опасными (превышают ПДК, ПДУ, система требует отдельных регулировок). Для предупреждения

несчастного случая достаточно применить защитные

средства или выполнить профилактические мероприятия (выполнить регулировки, затянуть резьбовые соединения, установить защитные кожухи и другое).

3. Класс 3. Система находится в опасном

восстанавливает первоначальные функции собственными силами, без внешней помощи.

Класс 3в. Производственные факторы в абсолютных значениях или в отклонениях покидают

состоянии, когда параметры покидают

трубку" ε .

"трубку"

ε

и превышают безвредные значения на

Вероятность появления опасности равна или больше 0,5, но меньше 1. Несчастный случай может произойти в любой момент времени. Защитные средства, профилактические мероприятия не устраняют опасности. Требуется прекращение эксплуатации системы, чтобы устранить опасность.

4. Класс 4. Система находится в аварийном

такую величину, при которой, после прекращения действия фактора, организм восстанавливает первоначальные функции после лечения или после применения внешней помощи.

Класс 4в. Производственные факторы в абсолютных значениях или в отклонениях покидают

"трубку"

ε

и превышают безвредные значения на

состоянии, когда параметры системы достигли предельных значений, тогда вероятность появления опасности равняется 1. Это означает, что при включении системы в работу она перейдет в аварийное состояние и произойдет несчастный случай, если человек будет находиться в зоне действия опасности. Система или её опасный элемент должны быть заменены безопасными.

Теоретические исследования состояния системы позволяют предложить четыре класса вредностей.

Класс   1в.   Производственные факторы в абсолютных значениях или в отклонениях не

такую величину, при которой после прекращения действия фактора, организм не восстанавливает первоначальных функций даже после лечения.

Развивается профессиональное заболевание.

Предложенные теоретические подходы могут послужить научной основой в разработке классов риска при проведении аттестации рабочих мест по

условиям и охране труда в отраслях агропромышленного производства.

покидают "трубки" õ и не превышают безвредных уровней (ПДК, ПДУ). Система безвредна.

Класс 2в. Производственные факторы в отклонениях или абсолютных значениях выходят из

"трубки" õ , но не покидают "трубку"

ε

и

превышают безвредные значения (ПДК, ПДУ) на

такую величину, при которой после прекращения

действия

фактора,     организм человека