Новые технологии при решении задач гравиметрии и их применение при поиске полезных ископаемых

Рассматриваемое в статье направление исследований связано с использованием современных подходов при решении задачи выделения возмущающих объектов посредством продолжения гравитационного поля в нижнее полупространство на основе составления и решения систем линейных алгебраических уравнений (СЛАУ) больших порядков. Выдающиеся достижения в области вычислительной техники в последние 30 лет, значительное увеличение вычислительных ресурсов (быстродействия и объема оперативной памяти компьютеров) позволяют исследователю решать разнообразные задачи чис- ленными методами за приемлемое время, в том числе и СЛАУ больших порядков.

Методологическую основу выделения перспективных объектов (в т.ч. залежей рудных полезных ископаемых) составляет метод дискретных аппроксимаций физических полей, предложенный академиком В.Н. Страховым[12]. Суть этого метода заключается в замене трехмерного (или двумерного) непрерывного пространства дискретным (сеточным) пространством. Уравнение Лапласа, описывающее физические поля вне возмущающих тел, заменяется на его дискретный аналог путем представления вторых частных производных в виде вторых разделенных разно-

стей. Краевые условия, представленные в виде непрерывных функций, заменяются сеточными функциями. Таким образом, задачу аналитического продолжения заданных на поверхности Земли физических полей в нижнее полупространство, которая используется для выделения возмущающих объектов, дискретный метод редуцирует её к задаче составления и решения СЛАУ.

Следует отметить, что попытка непосредственного применения дискретного метода к задаче аналитического продолжения приводит к проблемам постановочного характера. Дело в том, что в классической постановке задача по восстановлению значений гравитационного поля по заданным дискретным измерениям («задача Дирихле для уравнения Лапласа в квадрате» - двумерный случай) решается неустойчиво, т. к. на практике исходные данные (результаты гравиметрической съемки) бывают заданными не на всем прямоугольном контуре, охватывающем аномалиеобразующие объекты, а лишь на его части (как правило, на дневной поверхности). Была разработана методика, которая позволила, во-первых, добиться устойчивого решения возникающей здесь СЛАУ; во-вторых, оценить точность восстанавливаемых значений поля [14,15,3,10,11]. Ниже приводится модельный пример, иллюстрирующий применение дискретного метода, в котором в качестве возмущающего объекта принимается прямоугольная призма.

Решением прямой задачи для прямоугольной призмы сечения 2.4x2.1 км в плоскости Oxz и бесконечного простирания в направлении оси у (двумерный случай) находятся «входные» значения поля вертикальных градиентов гравитационно-дУ го потенциала ---, расположенные на dz уровнях z = 0 и z -h ( ось z направлена вниз). Аналитическое продолжение осуществляется в нижнее полупространство в заданный горизонтальный слой (прямоугольник), нижняя отметка которого находится на глубине 4 км. Длина профиля заданных значений поля на уровнях z = 0 и z -h равна 32 км; шаг сетки hi = h2 = 0.2 км, так что число точек наблюдений (заданий) равно 161(на одном уровне). Расстояние от z = 0 до верхней кромки призмы 4 км. Таким образом, число уровней, на которых определяются искомые значения аналитически продолженного в

„               дУ дискретной постановке поля --- и значе- dz ния поля, полученные решением прямой задачи, будет равно 20. Следовательно, число искомых неизвестных здесь равно 161x20 = 3220, а число уравнений, очевидно, будет равно 159x20x2 = 6360, т. к. дискретное уравнение Лапласа Qi-ц + CluMk + C1ujk_1 +Clujk+l = 0 (1)

рассматривается совместно на 2 шаблонах «прямой крест» и «косой крест» во всех внутренних точках профилей на уровне z = 0 и во всех внутренних точках x_s е Intlls заданного горизонтального слоя.

Коэффициенты в уравнении (1) Ci=l, Со=-4 для обоих шаблонов.

При проведении расчетов удобны следующие обозначения:

^(л?)- У .к ’ us(xs +hel) = ui+bk^

^us (.^xs ^— ^^el) ^— У-I,к ’        (2)

(us(xs+he2) = uhk+l-, us(xs-he2} = ukk-y где xs -узлы сетки ^ e Intils); h - шаг сетки; q в2 - единичные векторы в направлении осей x,z соответственно.

Таким образом, возникает переопределенная система линейных алгебраических уравнений

Au = fs, (3)

где размерность матрицы А= 6360x3220, а размерность вектора fg= 6360xl (из которых ненулевых, очевидно, всего 636 компонент). Обозначение вектора правой части в виде f_s означает, что в общем случае заданные значения поля могут быть осложнены помехой.

Для решения прямой задачи, т. е. нахо-„ ЗЕ ждения точных значении поля --- в уз- dz лах заданной области Щ и заданных значений поля на уровнях г = 0иг=-йс помощью формулы (4), была составлена компьютерная программа prGdAN

Ag = А

xln( х2 + z2) + 2zarctg—

Z

Решения прямой задачи [ 1 ] на уровнях z = 0 и z = -h используются в качестве «измеренных» значений в модельных условиях, решения прямой задачи в узлах заданной области Щ используются для оценки точности восстанавливаемых зна чений поля. Избыточная плотность ст принималась равной 0,1 г/см3, гравитационная постоянная f= 66,7х10'9 см3хг'1хс'2, размерность значений гравитационного поля

dV

= см/с'2.

Для формирования матрицы А и вектора fs в правой части уравнения (3) были составлены программы (соответственно рг 606 и рг 607) при рассмотрении дискретного уравнения Лапласа на составном шаблоне «прямой крест» и «косой крест». Матрица А в СЛАУ (3) очень сильно разрежена. Фактически при проведении различных вычислительных экспериментов с использованием различных аппроксимаций уравнения Лапласа было выяснено, что в строках матрицы А операторного уравнения Au = f8 могут находиться от 1 до 25 ненулевых элементов, тогда как общее число элементов в строке может составлять несколько тысяч. СЛАУ (3) решалась с использованием пакета программ SPM, разработанного на основе метода итерационного типа [13]. Время решения СЛАУ с матрицей А = 6360x3220 и вектором правой части f8= 63 60 х 1 составило 00:19:25 (ноутбук DELL, процессор AMD Turion, тактовая частота 2 Ггц). Результаты расчета по восстановлению значений поля приведены в табл. 1.

Как видно из табл. 1, на глубине, равной шагу сетки (200 м) от уровня z=0, относительная погрешность равна 2,293888 10'5, т.е. восстановленные значения поля отличаются от точных в среднем на 0.002 %, а на глубине, расположенной выше отметки верхней кромки пласта на 1 шаг сетки (т.е. на глубине 3.8 км), это отличие составляет порядка 3%.

Эти же результаты расчетов в графической форме приведены на рис.1. Аномальные кривые, построенные для восстановленных значений поля, также свидетельствуют о высокой точности, с которой получены значения поля при аналитическом продолжении в нижнее полупространство, а их форма ничем не отличается от формы кривых, полученных в результате решения прямой задачи гравиразведки

Таким образом, результаты расчетов показывают, что при аналитическом продолжении с использованием дискретного уравнения Лапласа поле восстанавливается в нижнем полупространстве вплоть до верхней кромки возмущающего объекта практически с любой априорно заданной точностью. Для этого достаточно взять подходящие (оптимальные) длину шага сетки и длину профиля (но, очевидно, точное решение не принадлежит области получаемых приближений) . Позже, используя методы функционального анализа, была теоретически доказана сходимость используемых здесь дискретных схем к точному решению при неограниченном уменьшении шага сети [6].

Далее модельные исследования проводились в условиях, когда аналитическое продолжение заданных значений поля в нижнее полупространство происходит до отметок ниже верхней кромки возмущающего объекта, т.е. когда значения поля восстанавливаются в многосвязных сеточных областях или всюду в заданной области в нижнем полупространстве за вычетом областей, занятых возмущающими массами.

Таблица 1. Относительные погрешности восстанавливаемых значений поля при аналитическом продолжении

№	Глубина, км	Относительная погрешность
		хточ	Е
		Шаблон “прямой кресч	”+”косой крест”
1	0,2	2,293888 Е-005
2	0,4	6,358421 Е-005
3	0,6	1,213529 Е-004
4	0,8	1,990522 Е-004
5	1,0	3,024380 Е-004
6	1,2	4,395415 Е-004
7	1,4	6,225612 Е-004
8	1,6	8,703333 Е-004
9	1,8	1,210503 Е-003
10	2,0	1,681312 Е-003
11	2,2	2,334194 Е-003
12	2,4	3,239488 Е-003
13	2,6	4,494939 Е-003
14	2,8	6,239593 Е-003
15	з,о	8,673592 Е-003
16	3,2	1,208882 Е-002
17	3,4	1,691917 Е-002
18	3,6	2,383403 Е-002
19	3,8	3,394990 Е-002

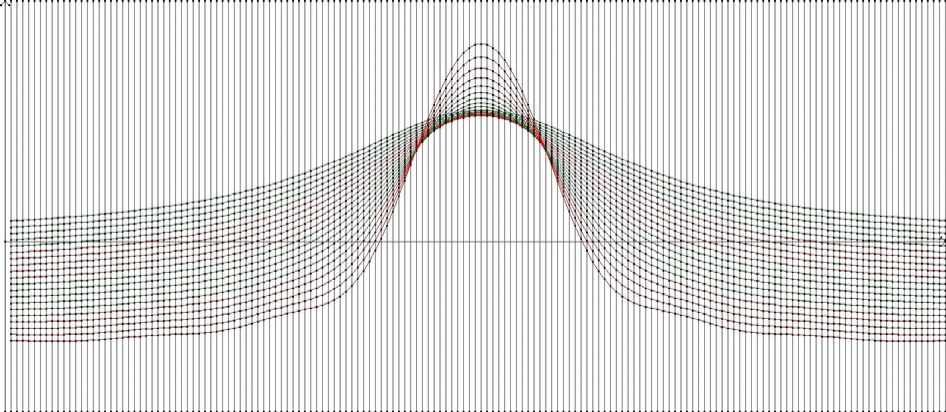
Рис. 1. Кривые восстановленных значений аномального гравитационного поля (в 161 точке на каждом уровне) при шаге сетки, равном 200м на 20 уровнях: от 0.2 км до отметки, отвечающей положению верхней кромки 4км (всего 20 кривых) (для удобства чтения каждые 5 аномальных кривых окрашены в два различных цвета)

В результате проведенных вычислительных экспериментов установлено, что на отметках ниже верхней кромки аномалиеобразующего тела начинается распад поля. Полученный результат при аналитическом продолжении поля ниже верхней кромки тем не менее содержит в себе полезный вывод: начало распада поля можно связать с прохождением отметки верхней кромки и таким образом получить правило для определения положения верхней кромки гравитирующего объекта. Этот результат вместе с другими послужил предпосылкой к созданию технологии определения контура аномалиеобразующего объекта, имеющей уже практические приложения. Отметим здесь же, что положение верхних особенностей гравитирующего объекта по оси х можно определить построением функции, подобной функции Березкина[9].

Как уже было сказано, изложенные результаты пересчета поля в нижнее полупространство были использованы при разработке технологии выделения и оконтуривания в разрезе локальных гравитирующих объектов. Для решения задачи оконтуривания из программных модулей был собран пакет программ «GrAnM». Программная часть: каждая задача разбивается на подзадачи, которые решаются отдельно при помощи исполняемых модулей. Модули написаны на языке С. Общая схема решения подзадачи: на вход исполняемому модулю подаются текстовые файлы с некоторой информацией, используя которую формируется выходной файл с результатами работы модуля. Общие входные параметры: шаг сетки, длина профиля, гравиметрические данные (а также размеры гравитирующего объекта, глубина его залегания и избыточная плотность в модельных примерах) расположены в текстовом файле.

Приведем теперь описание технологических этапов определения особых точек и контура аномалиеобразующего тела в режиме реального времени с использованием пакета «GrAnM» :

• 1.    Исходные данные - результаты гравиметрической съемки, взятые по профилю, как правило, с неравномерным шагом измерений - пересчитываются в узлы равномерной сетки и по необходимости -в узлы сетки с меньшим шагом с использованием сплайн-интерполяции. Полученные значения гравитационного поля в узлах равномерной сетки пересчитываются в верхнее полупространство в узлы сетки с тем же шагом с использованием интеграла Пуассона.

• 2.    Выбираются отметки z в нижнем полупространстве (в долях от заданной длины профиля) и осуществляется аналитическое продолжение заданных значений поля до этих отметок с составлением и решением соответствующих систем линейных алгебраических уравнений. Вектор решения СЛАУ разбивается на подвекторы, отвечающие уровням глубин в нижнем полупространстве, каждый из которых расположен на расстоянии шага сетки от соседнего. По значениям поля на каждом уровне строятся аномальные кривые и графики функции, подобной функции Березкина (начиная со 2-го уровня от поверхности Земли).

• 3.    Определяется с высокой точностью (которую можно увеличить, переходя к более мелкой сетке) положение верхней кромки гравитирующего объекта. При этом учитывается, что при переходе через отметку, соответствующую верхней кромке аномалиеобразующего объекта, в аномальных кривых по периферии начинают зарождаться дополнительные колебании (осцилляции).

• 4.    После определения положения верхней кромки возмущающего объекта находятся координаты верхних особенностей построением функции, подобной функции Березкина.

• 5.    Определяется положение центра тяжести гравитирующего объекта как отметки, до прохождения которой при аналитическом продолжении вторичные колебания в аномальных кривых пока еще не достигают значительных амплитуд.

• 6.    Положение нижней кромки аномалиеобразующего тела определяется приближенно по положениям верхней кромки, верхних особенностей и центра тяжести тела с привлечением имеющейся априорной информации.

Модельный пример, рассмотренный выше, в ряде других многочисленных модельных исследований [2,3,4,5] относится к случаю одиночных возмущающих тел однородной плотности. С практической точки зрения гораздо больший интерес, очевидно, представляет выделение неоднородных по плотности распределений. В недавних модельных экспериментах, проведенных для таких распределений [7,8] ,было установлено, что закономерности, отмеченные при восстановлении значений поля для одиночных тел однородной плотности, аналогичны для неоднородных по плотности распределений. Таким образом, технология оконтуривания (пи. 1-6) применима и здесь за исключением и. 6,

Рис. 2. Расчетная схема модельного примера кусочно-однородного разреза(сечение 16x2км) в двумерном случае

где для установления положения верхней кромки, помимо условий указанных в соответствующем пункте, потребуется учет априорной информации и опыт интерпретатора.

В ходе модельных исследований для неоднородных распределений плотности было также установлено, что указанная технология позволяет определять положение верхних особенностей отдельных тел (однородных по плотности), слагающих данный кусочно-однородный разрез. В связи с этим был поставлен вычислительный эксперимент, целью которого было нахождение плотностных характеристик для уже выделенных границ в разрезе с использованием данной технологии (с той или иной степенью приближения). Пред положим, что нам известен априори заданный конечный набор плотностей (из 8 значений) для данного района исследований, что вполне возможно в реальных физико-геологических условиях. Априори заданный набор увеличивающихся с глубиной плотностей представляет собой значения: 2.1, 2.17, 2.24, 2.31, 2.38, 2.45, 2.52, 2.59 г/см3.

На рис. 2 представлен двумерный кусочно-однородный разрез, состоящий из набора прямоугольных призм, характеризующий 5 слоев однородной плотности от 2.11 до 2.25 г/см3. Геометрические размеры разреза (призматического фрагмента геологической среды) указаны на рисунке, шаг сетки h\= hi = 0.4 км, расстояние от z = 0 до верхней кромки аномалиеобра- зующего пласта 4 км. Для этого разреза с набором плотностей от 2.11 до 2.25 г/см3 решалась прямая задача по формуле (4) „ dV по нахождению значении поля -- в dz точках, расположенных на уровне z=0. Найденные значения гравитационного поля принимаются в модельном примере в качестве «наблюденных».

Постановка задачи выглядит следующим образом: получить значимые решения для интерпретационных моделей раз резов кусочно-однородной структуры путем прямого перебора всех возможных вариантов моделей, состоящих из 5 слоев и 8 наборов плотностей. Количество в 5 слоев выбирается исходя из необходимости оптимизации времени расчета: если разрез состоит из 5 слоев , то следует решить 85= 3 2 7 68 прямых задач, а если разрез состоит, например, из 8 слоев, надо решать уже 88 (что примерно равно 16x106) прямых задач гравиразведки, что резко увеличивает время счета.

Таблица 2. Относительные погрешности в среднеквадратичной метрике между «наблюденными» значениями и решениями прямой задачи для интерпретационных моделей из 4 класса эквивалентности

№	Плотностной состав интерпретационных моделей, принадлежащих к 4-му классу	Относительная погрешность
1	2.1 2.1 2.31 2.52 2.52	4.35146556278964Е-08
2	2.1 2.1 2.31 2.59 2.45	5.1909576865242Е-08
3	2.1 2.1 2.38 2.38 2.59	4.1920575544551Е-08
4	2.1 2.1 2.38 2.45 2.52	5.46288653639013Е-08
5	2.1 2.1 2.45 2.31 2.59	5.76107322622971Е-08
6	2.1 2.17 2.17 2.59 2.52	4.19182790455427Е-08
7	2.1 2.17 2.24 2.45 2.59	4.19182790455427Е-08
8	2.1 2.17 2.24 2.52 2.52	5.80024670173613Е-08
9	2.1 2.17 2.31 2.38 2.59	6.1271546025346Е-08
10	2.1 2.24 2.1 2.52 2.59	3.96172506033659Е-08
11	2.1 2.24 2.1 2.59 2.52	6.16910726751234Е-08
12	2.1 2.24 2.17 2.45 2.59	6.52473637927171Е-08
13	2.17 2.1 2.1 2.59 2.59	8.99337695792759Е-08
14	2.17 2.1 2.17 2.59 2.52	3.90798825656027Е-08
15	2.17 2.1 2.17 2.59 2.52	6.62538179169598Е-08
16	2.17 2.1 2.24 2.45 2.59	7.01255728258207Е-08
17	2.17 2.17 2.1 2.52 2.59	7.47634783576381Е-08

Множество всех получаемых интерпретационных моделей распределяется по 4 классам эквивалентности. В качестве критерия, классифицирующего полученное множество решений, принимается относительная погрешность в среднеквадратичной метрике между «наблюденными» значениями и решениями прямой задачи для данного плотностного состава разреза (1-й класс, если относительная погреш ность А > 10'3 ; 2-й класс - 10'5 < Д< 10'3 ; 3-й класс - 10'5 < Д< 10'3; 4-й класс -Д<10'7). Расчеты показали, что интерпретационные модели расположились по классам эквивалентности следующим образом: 1-й - 13243 моделей, 2-й - 17321 моделей, 3-й - 2179 моделей, 4-й - 17 моделей.

Очевидно, что в качестве значимых решений следует рассматривать интер- претационные модели из 4-го класса эквивалентности с минимальной относительной погрешностью порядка 10'8. Здесь нет неприемлемых результатов, когда все 5 слоев имеют одинаковую плотность и т.п. (они попадают в другие классы эквивалентности).

Наиболее близок к искомому разрез, расположенный в 5-й строке табл. 2 (напомним, что искомый разрез с набором плотностей слагающих его горизонтальных слоев 2.11,2.18, 2.46, 2.53, 2.25 не входит в априори заданный набор плот