Новые точные решения, описывающие двумерное поле скоростей для решения Прандтля

Уравнения плоской задачи идеальной пластичности в стационарном случае имеют вид

5c ^f56do

2kI —cos26 + — sin26 I = 0, dx 15xd dc     (56 .       56]

2kI —sin26cos26 I = 0, dy     (5x dyJ

(dv   d v_v)       (6v d v_v )

I — x - + -^- I tg2 6 + I — x---y I = 0,

( dy   dx J       ( dx   dy J dVx d vy n

+    = 0

5x dy где c- гидростатическое давление; 6- угол между осью

Ox и первым главным направлением тензора напряже- ний; к - постоянная пластичности; vx, vy - компоненты вектора скорости деформаций.

Одним из практически важных и часто используемых в различных расчетах является решение Прандтля, которое описывает, в частности, сжатие тонкого пластического слоя материала жесткими плитами. Это решение имеет вид ax = -Р - к (x - 241- У2), ay = -p - kx, т = ky,                (3)

где p – произвольная постоянная.

Известно, что для полного описания пластического состояния тела необходимо знать поле скоростей.

Подставим уравнения (2) в систему (1):

-

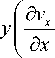
d vx5

x ^+

5y5

d v   ^d vy   _n

—- + —- = 0 d x   d y

Из системы (4) следует, что, в силу ее линейности, она имеет бесконечное число решений, которые могут быть полезны для анализа напряженно-деформированного состояния пластической среды.

В настоящее время известно два класса решений этой системы: решение Надаи [1] и решение Ивлева–Сенашо-ва [2], которые имеют вид vx = (cos 9- sin 9) exp-2 (4 + n), vy =( cos 9 + sin 9) exp-2 (4 + n).

Из решения Прандтля (3) получим

p

4 + n = -T-x - sin29, k(8)

cos 2 9 = y .

Окончательно находим новое поле скоростей:

Г1Г p ■ ,„il/„ .

v„ = exp —---x - sin29 (cos 9-sin 9), x       (2( к             JJV’

Г1Г p ■ ™!lz v = exp —---x - sin29 (cos 9 + sin 9).

y       1 2 1 к            JJ

Аналогично определяются и другие поля скоростей.

Для уравнений (7) решения указаны в [3]. Далее будет построено пять классов новых решений уравнений (5) с учетом решений [3].

Первый класс :

L 4+n । _л Г 4-nVn ■ Г 4-ni u = cos X A cos u+ B sin u ,

I 2 J I 2 J I 2 J где A, B, p, X - произвольные постоянные; p2 - X2 = 1.

Тогда vx = -axy + в x - a arcsin y

-

-a y41-4" - 2 в 4^

d u dn

x • h

— sin X

2 I

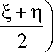
X

x ²

y ²

v = a — + — y I 2 2

-

в y + C 2 ,

, Г 4-n i _n ■ Г 4-n x A cos u-—¹ + B sin u-—^L

(    2 J Г 2

где a , в , C ] , C ₂ — произвольные постоянные (при a = 0 получаем решение Надаи).

Приведем другие решения системы (4). Для этого заметим, что в переменных 4 , n , где a = к ( 4 + n ) , 2 9 = 4 - n , уравнения (2) запишутся в виде

+— cos | X

2 I

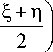
, . Г 4-n i „ Г 4-n A sin u  - B cos u

Г 2 J Г 2

d v_x x "54

-

d v„ tg 9 "£ = 0, 54,

Из уравнений (7) имеем

. Г-, 4+nl v = -X sin X——¹ x

I 2 J

d v       d v

—- + ctg 9 —- = 0.

dn       dn

. Г 4-n i n • Г 4-n x A cos u-—¹ + B sin u-—^L

Г 2 J г 2

+

Если ввести в (5) новые переменные по формулам

v x vy то получим систему

= u cos 9- v sin 9 ,

= u sin 9 + v cos 9 ,

Г. 4+n +u cos X----

I 2

л ■ Г 4-n

A sin u----

Г 2

-

Г 4-ni

B cos u----- .

Г 2 J

d v 1 ---u = 0, 54 2

d u 1 ---v = 0. dn 2

Далее поступаем по следующей методике: решаем систему (7), в ней вместо 4 и П подставляем выражения из решения Прандтля, совершаем замену (6) и находим поле скоростей, соответствующее решению (3).

Проделаем это на наиболее простом решении системы (7). Нетрудно видеть, что v = u = exp2 (4 + n)

есть решение системы уравнений (7). Подставим его в (6):

Подставим u , v в уравнения (6) и с учетом равенств

4-n

(8) и 9 = —2— получим

Г x v_T = cos — x I 2

- p - x - sin 2 9 J J [ A cos ( u9 ) - B sin ( p9 ) ] cos 9 -

у ■ Гх

-X sin I —

(X( p

+u cos —-- 1 2 1 к

ГХ v„ = cos — y 1 2

p - x - sin 2 9 J J [ A cos ( ц9 ) - B sin ( ц9 ) ] +

- x - sin 2 9 I l[- A sin ( u9 ) - B cos ( p9 ) ] I sin 9 ,

- p - x - sin29  [ A cos (p9)-B sin (p9)] sin 9 + к            JA-

Г     ГхГ p       -„IV

+ I -X sin I — I - к- - x - sin 2 9 I l[ A cos ( p9 ) - B sin ( p9 ) ] +

I X I P                    II

+ц cos I -2 1 - — - x - sin 2 9 I J[- A sin ( ц9 ) - B cos ( ц9 ) ] J cos 9.

где A , B , ц , X - произвольные постоянные; X ² - ц ² = 1. Тогда

Второй класс :

■ Ii 4 + 5 u = sin X----

I 2

, I 4-5 1 „ • I 4-5

A cos ц---- + B sin ----

I 2 J I 2

где A , B , ц , X - произвольные постоянные; ц ² - X ² = 1. Тогда

1     114+5

v = -X cos X----

I 2

. I 4-51 _n • I 4-5

A cos ц---- + B sin ц----

I 2 J I 2

■ L4+5 +ц sin X----

I 2

■ (X v = sin — x I 2

л ■ I 4-5 A sin ц----

I 2

_

I 4-5)

B cos ц----- ,

I 2 J

- k - x - sin 20J J [ A cos ( ц9 ) - B sin ( ц9 ) ] cos 9 -

I I XI P          _„1

-I -X cos I — I - k - x - sin 29 11[ A cos ( ц9 ) - B sin ( ц9 ) ] +

+ц sin IXI- p - x - sin 29Ц [- A sin ( ц9 ) - B cos ( ц9 ) ]^ sin 9,

v y = sin IX I- p - x - sin 2 9 J J [ A cos ( ц9 ) - B sin ( ц9 ) ] sin 9 +

+I X cos 1 2 1- p - x - sin2 9J J[ A cos ( ц9 ) - B sin ( ц9 ) ] +

+ц sin| 2 J - ^p - x - sin2 9 1 |[- A sin ( ц9 ) - B cos ( ц9 ) ] cos 9. I 2 1 k            )У                      -I

Третий класс :

2 4+5 u = exp X----

I 2

, I 4-5 I „ • I 4-5

A cos ц---- + B sin ----

Г 2 J I 2

где A , B , ц , X - произвольные постоянные; ц ² + X ² = 1. Тогда

i Ii4+5

v = X exp X----

I 2

I, 4+5

+ц exp IX 2

. I   4-51 n • I 4-5

A cos ц---- + B sin ц----

I 2 J I 2

, . I 4-5 I ,x I 4-5 A sin ц---- - B cos ц----

I 2 J Г 2

,

I X I P                  I vx = exp I 21 - — ~ x - sin 29 I J[A cos (ц9)- B sin (ц9)] cos 9-

I IXI P __1V

-I -X exp I — I - k - x - sin 2 9 I J[ A cos ( ц9 ) - B sin ( ц9 ) ] +

IJ P x 1/1 - У

+ц exp l XI----+------

I I    2 k 2       2

I [- A sin ( ц9 ) - B cos ( ц9 ) ] sin 9 , J

( X vy = exP I 2

- ^P - x - sin 2 9 J J [ A cos ( ц9 ) - B sin ( ц9 ) ] sin 9 +

IIXI P       __!V

+I X exp I 2 1 - k - x - sin2 9 J J[ A cos ( ц9 ) - B sin ( цб ) ] +

+ц expl —|

cos 9.

Четвертый класс :

Ii 4+5 u = exp X----

I 2

, I 4-5 I I 4-5

A exp ц-—+ B exp -—^L

Г 2 J I 2

,

i Ii4+5

v = X exp X----

I 2

[„ 4 + 5

+ ц exp IX 2

I X v_y = exp — x I2

_

. I 4-5 I _n I 4-5

A exp I ц 2 I + B exp I ц 2

. I 4-5 I I 4-5

- A exp I ц 2 I + B exp I ц 2

+

,

1 p ( -ц9 ) ] cos 9-

-I -X exp| 2J - ^p - x - sin 29 | T A exp ( -ц9 ) + B exp ( -ц9 ) ^ I I 21 k jy

(X

+цexpI 2|

- p - x - sin 29 J J [- A exp ( -ц9 ) + B exp ( -g9 ) ]J sin 9,

v y = exp 12I- p - x - sin29|J[ A exp ( -ц9 ) + B exp ( -ц9 ) ^ sin 9 +

I      IxI p        _„1V

+ X exp — -k- x - sin2 9 [ A exp ( -ц9 ) + B exp ( -ц9 ) ]

I         I 2 1 k                 J

+ц exp I 2| - p - x - sin 29 W- A exp ( -ц9 ) + B exp ( -ц9 ) ] J cos 9.

I ² I k             J J

Пятый класс :

Ii 4 + 5 u = exp X----

I 2

A 4-5 + B ,

где A , B , X - произвольные постоянные; х ² = 1. Тогда

1     11 4 + 5

v = X exp X----

I 2

( X vx = exP I 2

-

p

k

A 4-5 + B

-

- A exp I X ^{4 + 5}

I 2

x - sin2 9 J J [ - A 9 + B ] cos 9-

,

I1 I X

- X exp —

I 1 2

-

p

k

-

x - sin 2 9 J ! [ - A 9 + B ] -

X I XI p . _„)]I „ - A exp —--- x - sin2 9    sin 9 ,

I 2 1 k J J J

(X vy = exP I 2

11      (X

+ X exp —

I            I 2

-

-

-

p

k

p

k

-

x - sin2 9 I l [ - A 9 + B ] sin 9 +

-

x - sin 2 9 J i [ - A 9 + B ] -

- x - sin 2 9 J J J cos 9 .