Новые возможности гидропневматической очистки внутренней поверхности непроточных гидроагрегатов

Как показали предварительные исследования по визуализации картины течения, в данном случае при заполнении полости развиваются огромные скорости течения жидкости, способные обеспечить отрыв частиц со стенок полости в самое короткое время.

Эксперименты, основанные на технологии лазерного ножа и скоростной видеосъемки картины течения жидкости в прозрачном корпусе, имитирующем объект очистки, показали следующее:

• -    скорости течения жидкости на входе в агрегат при соответствующем выборе параметров стенда могут значительно (в 10 раз и выше) превышать рабочие скорости систем гидропривода;

• -    в процессе заполнения в полости развивается интенсивное струйно-вихревое течение жидкости и пузырьков газа, распространяющееся по всему объему полости;

• -    время заполнения полости может достигать значений 0,5 ^ 1,5 секунд.

В процессе дальнейшей разработки была изготовлена лабораторно-экспериментальная установка, пневмогидравлическая схема которой представлена на рис. 1.

Схема включает в себя:

• -    пневмогидроаккумулятор (ПГА);

• -    электрогидравлический быстродействующий распределитель;

• -    полость очищаемого агрегата;

• -    соединительные трубопроводы;

• -    измерители давления.

Магистраль подачи жидкости в полость агрегата выполнялась из трубопровода d_у=10мм. и длиной I =500 мм (включая длины соединительных штуцеров и переходников).

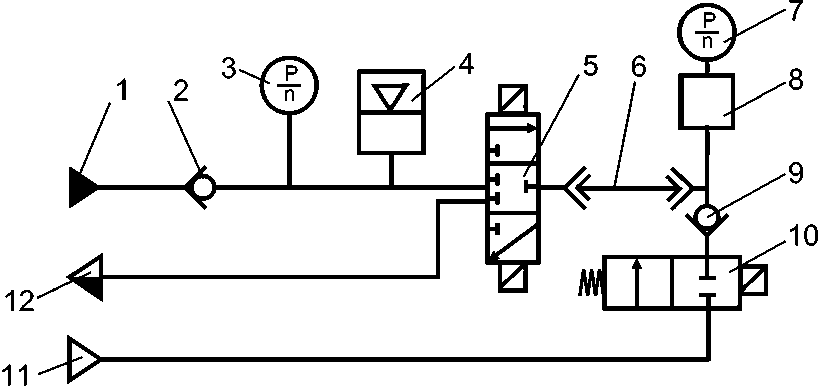
Рис. 1. Принципиальная схема процесса пневмогидравлической очистки агрегатов:

1 – магистраль подачи жидкости; 2, 9 – обратные клапаны; 3, 7 – измерители давления;

4 – пневмогидроаккумулятор; 5 – гидрораспределитель; 6 – трубопровод; 8 – объект очистки;

10 – кран; 11 – газовая магистраль; 12 – линия слива

В качестве измерительно-вычислительного комплекса использовалась аппаратура компании Hydac, состоящая из:

• 1.    датчика давления HDA 3800 со следующими характеристиками:

• -    класс точности 0,3 % мак;

• -    диапазон давления от 0 до 350 бар;

• -    выходной аналоговый сигнал 4…20 мА (2-х проводные) или 0…20 мА (3-х проводные);

• 2.    портативного регистратора данных HMG-3000;

• 3.    персонального компьютера с программ-

• ным обеспечением Hydac.

Общий вид экспериментальной установки представлен на рис. 2.

Эксперименты проводились сериями при различных значениях давления зарядки воздушных и гидравлических полостей пневмогидроаккумулятора.

На рис. 3 представлена осциллограмма изменения давления в полости агрегата при давлении зарядки воздухом 3 МПа и зарядки гидравлической 5 МПа.

Рис. 2. Общий вид экспериментальной установки

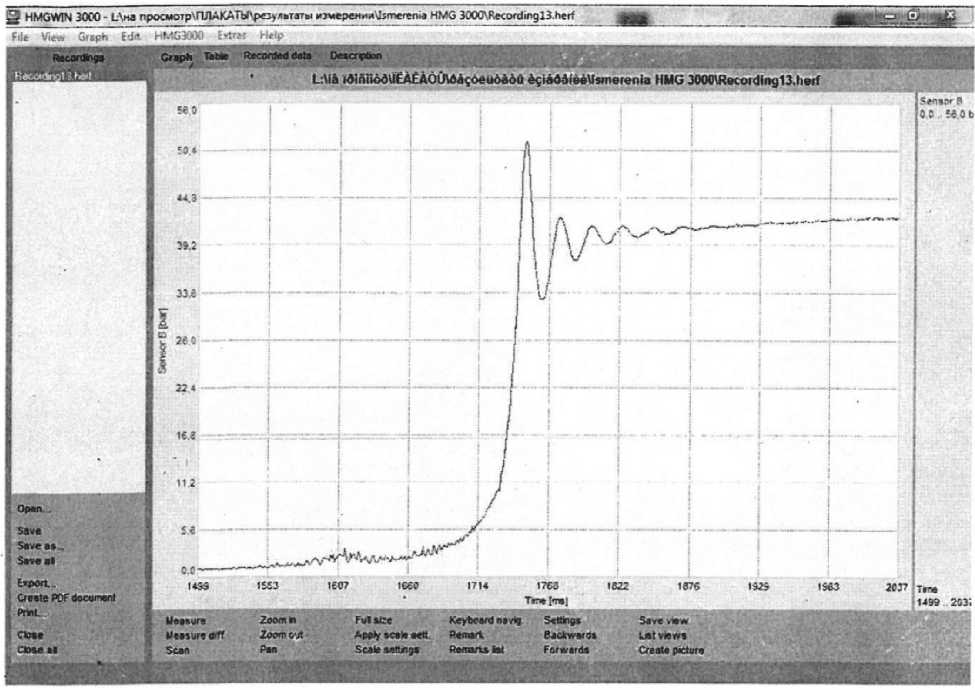
Рис. 3. Результаты эксперимента, полученные при зарядке ПГА до 5, 0 МПа и объёмом полости 0,54 X 10 -3 м 3

Приведенная осциллограмма процесса заполнения полости показывает, что длительность заполнения составляет около 1 секунды по времени при достижении максимума расхода до 1 л/с (60 л/мин).

С целью углубленного теоретического анализа гидродинамика процесса, оценки влияния различных конструктивно-технологических факторов в работе выполнено математическое моделирование процесса в программной среде MatLab-SimuLink. Моделирование выполнялось при следующих допущениях:

• -    растворимость газа в жидкости отсутствует;

• -    стенки полости абсолютно жёсткие;

• -    жидкость рассматривается несжимаемой;

• -    процесс заполнения протекает по изотермическому закону;

• -    подключение полости к источнику давления происходит моментально.

При моделировании учитывалось:

• -    инерционное сопротивление столба жидкости в трубопроводах, включая размеры проход-ников и соединительных штуцеров;

• -    линейное и нелинейное (квадратичное) активное сопротивление течения жидкости в трубопроводах;

• -    упругие свойства газовой среды при заполнении полости.

Основной особенностью модели является организация вычисления активных потерь давления в трубопроводах. Для этого вещественная часть импеданса магистрали, зависящая от геометрических характеристик трубопроводов и режима течения жидкости, определялась в виде уравнения прямой:

Re Z тр = a + bQ = Re Z л + Re Z н , (1) где a – составляющая импеданса при ламинарном течении;

• b – коэффициент нелинейной составляющей импеданса при турбулентном течении;

Q – расход жидкости;

Re Z_л – линейная составляющая вещественной части импеданса;

Re Z_н – составляющая вещественной части импеданса, учитывающая нелинейные эффекты.

Правомочность такого подхода показана в работе В.П. Шорина [6], где так же указано, что указанные составляющие могут быть определены расчётным путём для установившегося течения жидкости по известным соотношениям гидравлики [7]:

a = Re Z л = 128 ^^ ^ ;        (2)

лd4

, Re Z„ _Л1. £     ^ P

b = ££   = 161 X + ^ I      Qо. (3)

Q n       I d       ^ 2 d 2

В выражениях (2) и (3) обозначено:

P - плотность жидкости;

• V - коэффициент кинематической вязкости;

• X - коэффициент потерь на трение при турбулентном течении;

^ - суммарный коэффициент местных потерь, определяемый с учётом потерь в гидравлическом распределителе;

• £ , d - длина и диаметр магистрали;

Q ₀ – установившийся расход жидкости, при котором определяются координаты контрольной точки на уравнении прямой выражения (1).

Далее определяется угол наклона (2) прямой

• (1)    в координатах Re Z н ₀ = Re( Q 0 ) :

  tg « =

  
  

  Re Z н 0 Q 0

  
  

откуда перепад давления при текущем значении турбулентного расхода (Q) определяется в виде:

^Pн = tg«(Q )Q

Математическая модель расчёта процесса заполнения полости агрегата приведена на рис. 4.

В левой части модели (сверху вниз) размещены исходные данные для расчёта:

• -    диаметр магистрали, м;

• -    длина магистрали, м;

• -    давление предварительной зарядки газом ПГА, Па;

• -    полный объём полости ПГА, м³;

• -    давление зарядки ПГА жидкостью, Па;

• -    коэффициент кинематической вязкости жидкости, м²/с;

• -    критическое число Рейнольдса;

• -    объём полости очищаемого агрегата, м³;

• -    давление предварительной зарядки газом полости агрегата, Па.

Правая часть модели представляет собой четыре регистратора – измерителя параметров переходного процесса.

В средней части модели производится вычисления основных и вспомогательных параметров процесса.

В блоках Product и Gain производится вычисление площади проходного сечения трубопровода. В блоках Product 1 и Product 2 вычисляется величина, обратная “инерционности” (L) трубопровода:

• 1    = S tp.

L   p£ , где Sтр – площадь внутренней поверхности трубопровода;

• P - плотность жидкости;

• £ - длина трубопровода.

Блоки Product 10 и Product 11 позволяют вычислить давление на выходе идеального ПГА без учёта трения и массы поршня. Это давление вычисляется с учётом давления предварительной зарядки ПГА газом, полного объёма ПГА и давления зарядки ПГА жидкостью. Вычисление давления на выходе “реального” ПГА производится с учётом массы поршня (блоки Deruvative 1 и Gain 5) и трения поршня о стенку цилиндра ПГА (блок Gain 4). Это давление, уменьшенное на величину давления в полости объекта очистки и величину активных потерь давления в трубопроводе, подается на вход блока Product 4. В этом блоке, работающем совместно с блоком Integrator 1, определяется объёмный расход жидкости на входе в полость объекта очистки. Интегрированием найденного значения расхода вычисляется объём порций жидкости, поступающий в полость объекта очистки (блок Integrator 2). После вычитания этого объёма из полного объёма ПГА определяется объём газа в полости ПГА. Затем в блоках Product 7 и Product 8 рассчитывается давление в полости ПГА в процессе заполнения полости.

Вычисление активного перепада давления на концах трубопровода организовано следующим образом. С использованием блока Product 8 определяется максимальный расход жидкости при ламинарном течении. Это значение сравнивается с текущим вычисляемым значением расхода. Переключатель Switch и коэффициент Gain 2 определяют перепад давления жидкости при ламинарном течении с учётом изменения направления потока, для чего используется блок Gain 3.

Для вычисления нелинейного квадратичного перепада давления используются блоки Gain 1, Product 6. Перепады давления суммируются и затем уменьшают давление на входе в трубопровод. Переключатель Switch 1 выполняет функции гидрораспределителя потоков на рисунке 1 для расчёта фаз наполнения агрегата и последующего слива жидкости из него.

Результаты расчётов по модели достаточно точно согласуются с результатами физических экспериментов в части:

• -    длительности переходных процессов заполнения и слива жидкости;

• -    формы и параметров изменения давления в полости очищаемого агрегата.

0.785

В то же время результаты физических экспериментов по возбуждению гидроудара и визуализации течения жидкости показали, что в фазе слива около 15ч20% жидкости не сливается, а остаётся в полости. Это объясняется тем, что интенсивно перемешанная с газом жидкость сливается из полости вместе с газом. Данное явление

10E-3

Constant

600E-3

Product

Gain

Constantl

Products

Productl

Product2

Constant2

Scope2

5E6

Gain5

Constants

6E-3

ProductIO

Productl 1

Deri native 1

d

j/dt

3.2E4

Gain6

Constant9

1E7

ConsianilE

Scope

Step

Ramp

Switch 1    4 T X

Gain2

Switch

Product4 Integrate П

1 s Integrator

0.1E6

2.4E7

Constant?

10E-6

Gain4

Constants

Products

Gain3

Constant4

Producto

3E-3

Constants

38E9

Abs

1E6

Constants

Goir H-

0.785 <

Product?

Products

ЗсореЗ

Scooel

Рис. 4. Математическая модель расчета параметров течения жидкости моделью не учитывается, так как модель не предусматривает смешение жидкости и газа в процессе наполнения полости.

С использованием разработанной модели выполнен ряд вычислительных экспериментов, в ходе которых установлено влияние на достижимые скорости течения жидкости следующих конструктивно-технологических параметров процесса:

• -    влияние длины и диаметра соединительных магистралей стенда, которые изменялись соответственно: от 0,3 до 1,5 м и от 6 до 12 мм;

• -    влияние геометрических размеров ПГА, дав-

• лений зарядки полостей, трения и массы разделителя сред;

• -    влияние объёма полости очищаемых агрегатов (от 0,5 до 15 л);

• -    влияние давления предварительной зарядки газом полости очищаемого агрегата.

Результаты расчётов, часть которых представлены на осциллограммах на рис. 5, показали следующее:

• -    скорость потока жидкости при заполнении полости достигает значений 120 ^ 140 м/с, что почти в 10 раз превышает рабочие скорости течения жидкости систем гидропривода;

  

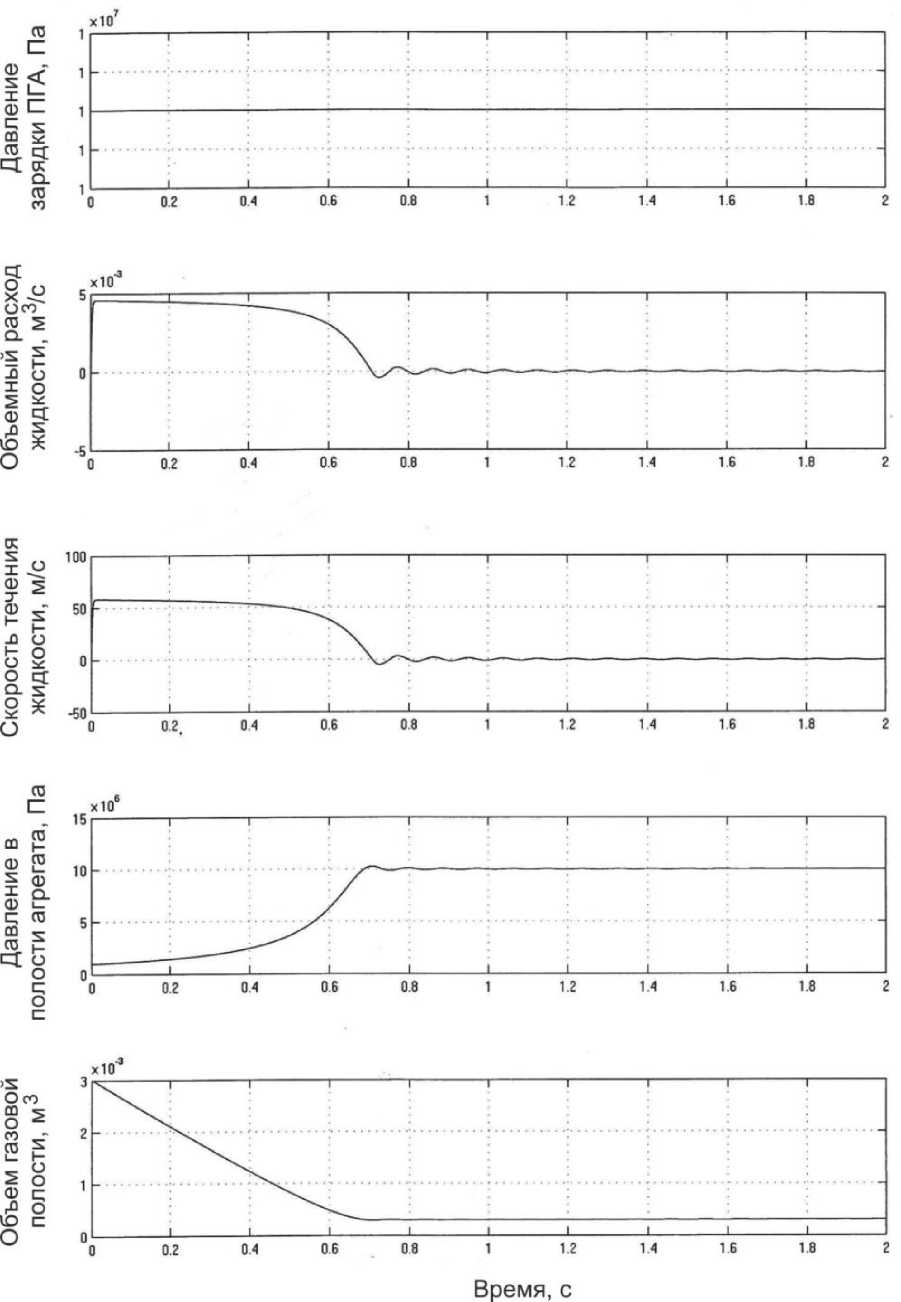
  Рис. 5. Некоторые результаты расчёта процесса заполнения полости агрегата

  
  

• -    длительность процесса заполнения полости составляет от 0,4 до 1,5 секунд.

Максимальные скорости течения жидкости могут быть достигнуты при увеличении диаметра соединительных магистралей и уменьшении их длины.

Увеличение давления зарядки ПГА жидкостью свыше 10 МПа, как правило, нецелесообразно, так как незначительно увеличивает скорости течения жидкости.

ВЫВОД

Полученные результаты позволяют предположить возможность значительного повышения качества и сокращения длительности процессов очистки агрегатов.