Новый алгоритм дискретного преобразования Фурье по основанию пять

При реализации хорошо известных и подробно описанных [1,2] "совмещенных" алгоритмов дискретного преобразования Фурье (ДПФ) вещественных последовательностей четной длины N используется избыточность представления входных данных по отношению к комплексным значениям базисных функций преобразования. Точнее, преобразование последовательности длины N сводится к преобразованию комплексной последовательности длины %, связанной с исходной, и некоторому (не очень большому) числу дополнительных умножений. Независимо от выбранной схемы совмещения, возможность применения такого приема обеспечивается наличием в поле комплексных чисел С нетождественного автоморфизма, реализуемого тривиально. Попытка синтеза быстрых алгоритмов ДПФ (БПФ) с "многократным совмещением", реализуемых в комплексной арифметике, наталкивается на принципиальные трудности, связанные с отсутствием в поле С достаточного числа тривиально реализуемых автоморфизмов. Синтез БПФ с многократным совмещением в иной, отличной от С, алгебраической структуре рассматривался автором в [3,4|. В качестве таких структур использовались композиционные алгебры [3J, циклотомические расширения поля рациональных чисел [4].

Следует также отметить, что наиболее сильные в количественном отношении результаты относятся к синтезу быстрых алгоритмов ДПФ длины N = 2к. В этом случае асимптотическая при N -> оо оценка вещественной мультипликативной сложности M(N) алгоритмов имеет вид:

M(N) = CNlog2N + O(N). (1)

Для большинства современных алгоритмов С = ^. Алгоритмы работы [4], для которых С = % *% и т- Д- представляют, по всей видимости, примеры БПФ, для которых снижение значения константы С в (1) все еще компенсирует увеличение структурной сложности алгоритма в разумном для пользователя диапазоне значений N.

В отличие от случая N = 2к, БПФ для N = рк ( р — простое ) разработаны менее детально и по своим вычислительным характеристикам относительно уступают БПФ для N = 2 . Например, наилучшая известная автору оценка мультипликативной сложности БПФ комплексной входной последовательности при N = 5к имеет вид [2]:

M(N) = 4,4Nlog5 N-3N + 3. (2)

Как справедливо утверждается в [5], популярность БПФ алгоритма Кули—Тьюки привела к тому, что БПФ—алгоритмы стали диктовать параметры применяемых устройств вместо того, чтобы приложения диктовали выбор подходящего алгоритма БПФ.

В настоящей работе синтезируются алгоритмы ДПФ для N = 5к с многократным (точнее, восьмикратным) совмещением в алгебре матриц второго порядка над квадратичным полем, у которых оценка для M(N) асимптотически лучше чем (2).

Возможность построения таких БПФ обеспечивается, в основном, тремя факторами: во-первых, возможностью вложения поля комплексных чисел в алгебру матриц второго порядка с коэффициентами из R; во-вторых, наличием в этой алгебре четырех автоморфизмов, реализуемых без вещественных умножений; в—третьих, уникальным арифметическим свойством первообразного корня пятой степени из единицы, вещественная часть которого является элементом квадратичного расширения поля рациональных чисел с минимальным многочленом, имеющим коэффициенты, равные (±1).

1. НЕКОТОРЫЕ СВОЙСТВА АЛГЕБР (2 х 2)-МАТРИЦ

Отметим ряд известных или легко доказываемых свойств алгебры (2 х 2) —матриц М ₂ (К). Автор счел возможным опустить доказательства, сводящиеся к непосредственной проверке матричных тождеств.

Предложение 1.1, Алгебра М2 (R) является четырехмерной ассоциативной R—алгеброй. Матрицы fl  0)       fO  1)        fl 0)       f 0  С

(О  1/      (1  0)       (О  -1J      (-1  oj образуют базис М 2 (R) над R, то есть любая матрица А из М 2 (R) представима в виде

A = y0E + y1T + y2R + y3I с подходящими YO»Y1,Y2,Y3 eR

Предложение__L2. Базисные матрицы Е, Т, R, I имеют конечные мультипликативные порядки:

Е = Т2 = R2 = 14.

Отображения 9, р, t алгебры М₂ (R) на себя:

9: А =

^ТАТ =

<Ь а)

р: Ah> RAR =

"Ь 1

, 1:Ан^ГА1 = dj

являются (внутренними) автоморфизмами алгебры М ₂ (R).

Предложение 1,3, Автоморфизмы 9, р, i действуют на базисные элементы Т, R, I следующим образом:

9(Т) = Т, р(Т) = -Т, i(T) = -T; e(R) = -R, p(R) = R, i(R) = -R;

e(D = -I, p(I) = -I, ,(!) = !.

Предложение 14. Пусть А е М₂ (R):

А =

a b

<с d.

тогда справедливы соотношения:

А + р(А) +6 (А + р(А)) = 2(а + d)E, [А - р(А) +0(А - р(А))]т = 2(Ь + с)Е, [А - 0(A) + р(А) - t( A)]R = 2(а - d)E, [А - 0 (А) - р(А) + i(A)]r* = 2( b - с)Е,

и решение системы (3) требует вещественных умножений только на степени двойки, которые считаются более элементарной операцией.

Отметим, что соотношения (3) справедливы и для матриц над кольцом достаточно общего вида.

Предложение 1.5, Пусть c = cos²^, s = sin ^^5, р = 2с,

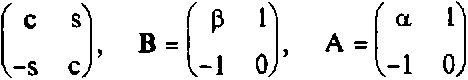
Тогда существует невырожденная матрица С такая, что в = с ’sc.

Доказательство, Утверждение непосредственно следует из того, что матрицы S и В имеют одно и то же характеристическое уравнение X² - рХ+ 1 = 0 с корнями

= ехр{±2%} .

Предложение 1.6. Матрица В имеет мультипликативный порядок, равный пяти, причем:

В5 = Е, В'=В4, В2 = рВ-Е, В3 = ₽В1-Е.

Пусть ос и р являются корнями уравнения t2 + t -1 = О,

Q(a) и Q[p)~ алгебраические расширения поля рациональных чисел с примитивными элементами а и р соответственно:

Q^(a) = { w = u + va; u, v € Q | ’ Qjp) = { w = и + vp; и, v е Q^}.                     (4)

Пару чисел (u,v), ассоциированную с представлением (4) элементов полей Q(P) и Q^T будем называть кодом элемента w и обозначать .

Так как аир являются корнями одного и того же уравнения, то сложение и умножение в кодах для Q^a) и Q(p) определяются с помощью одних и тех же правил:

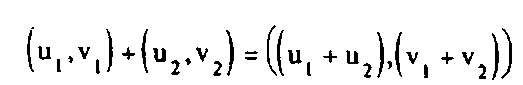
(u,,v1)x(u2,v2) = ((u1u2+v1v2),(u1v2+u2v|-v1v2))

Распространим правила сложения и умножения (5)—(6) пар на RXR, задав тем самым структуру кольца, которое обозначим ). Кольцо матриц с коэффициентами из кольца J обозначим М2 0); матрицы X, компоненты которых заданы кодами, будем обозначать <Х>.

Предложение 1.7. Пусть W — матричный корень степени N = 5К из Е:

где cN=cos^^j, sN =sin2^j. Тогда матрица V = С ^ С, где С — матрица, определенная в предложении 1.5, является корнем уравнений Ук = В, VN = Е.

Предложение L8. Существуют q₀,qj eR такие, что матрица V представима в виде

V = q0E + qiB.                                                                (7)

Доказательство, В самом деле, так как кЕ+^)к=8'

то

(cNE + sNC-'lc)K=B, а так как из предложения 1.5 следует, что cE + sC-1IC = B, то, полагая

sn/         csn/

Q         , Л = C —

• ^Ч 1 /S * ^ч0 N /S ’

получаем требуемое. Отсюда следует также справедливость представления (6) с подходящими qOm,qlm eR и для матриц V™.

Непосредственное умножение матрицы из М2 0) на степени матрицы требует шестнадцати вещественных умножений. Но, в силу предложения 1.8, матрица < V™ > имеет специфический вид:

_v„ Г<^х*у) (У’⁰))

• ^{<     >-}1(-У.О) (x.O)J

с некоторыми х,у eR. Эта специфика позволяет построить алгоритм сокращенного умножения.

Предложение 1,9, Умножение матрицы из М₂ 0) на степени матрицы требует четырнадцати вещественных умножений.

Доказательство . Действительно, так как

(( ьИ ^f*X,y* *У*°^-3,Ь ’ C'd ц-у,О) (x.O)J-

= ((ax + by - cy,bx - dy + ay - by);(ay + ex, by + dx)) = ((X,Y);(Z,T))

то при ai=(a-b)y, a2 = bx, a3 = dy, a4=y(b-c), a5 = ax, a6=c(x + y), a?=x(d-c)

имеем

X = a4+a5, Y=a1-a3+a2,

Z = a.+a +a , T=a +a +a.

1       4      6                4 .    6       /

Поэтому вычисление левой части (8) требует, согласно (9) и (10), семи вещественных умножений, а умножение матрицы из М2 (J) на степени матрицы — четырнадцати вещественных умножений.

Пусть далее < х >= (x^xj gJ,

< х >  = х, + ха, < х >  = х + х р;

аналогичный смысл имеют обозначения < V > и < V > для матриц, а           р

Предложение 1.10 . Существуют невырожденная матрица F еМ₂ (R) и целое число d, такие что справедливо соотношение

• <    V^d > =F ¹ WF, а

• Доказательство. Достаточно показать, что < V >^ является первообразным матричным корнем степени N из Е. А это следует из предложения 1.7 и непосредственно проверяемых равенств:

• 2.    БЫСТРЫЙ АЛГОРИТМ ВЫЧИСЛЕНИЯ ОДНОГО МАТРИЧНОГО ПРЕОБРАЗОВАНИЯ

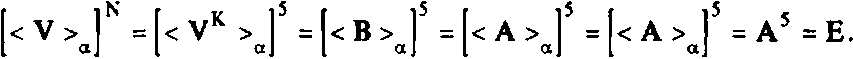
Основную роль при синтезе рассматриваемого алгоритма ДПФ длины N = 5к играет следующее утверждение.

Предложение 2.1 . Пусть < h(n) > — последовательность матриц периода N = 5^к с коэффициентами из J. Пусть {<Н(т) >} — "матричный спектр" последовательности {h(n)}:

N-1

(Н(ш)) = ^Ын^У1”1), (ш = 0,1,..., N - 1),                                  (Ц)

п=0

где V матрица, определенная в предложении 1.8. Тогда для вычисления {< Н(т) >} достаточно

M"(N) = yN(log5N-l)

вещественных умножений.

Доказательство . Представим (Н(т)) в форме:

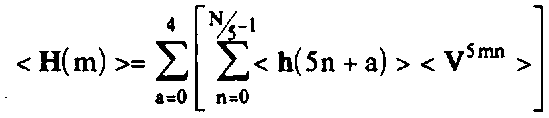
< Vam >=^<На(т)>< V81" >.

а=0

Внутренние суммы в (13) представляют собой преобразования (11) длины N/5. Их достаточно вычислить для значений т, лежащих в "фундаментальной области":

А,={0.1.....%-1}-

Действительно, значения < Ha(m)V8m > для т, лежащих в областях Дь, полученных из До аддитивным сдвигом на ^% (b = 1, 2, 3, 4 ), отличаются от соответствующих значений только умножениями на степени матрицы (В), которые реализуются без нетривиальных вещественных умножений. Соотношение (13), таким образом, редуцирует вычисление матричного спектра длины N к вычислению матричных спектров пяти последовательностей длины N/5 и некоторому числу дополнительных умножений на < Vam > для m е Д . Считая, что умножения матриц на степени (V) реализованы согласно предложению 1.9, получаем для M*(N) рекуррентное соотношение:

M*(N) = 5М"(%) + 4 х 14 х % с начальным условием М*(5) = 0, решение которого дает (12).

• 3.    БЫСТРЫЙ АЛГОРИТМ ВЫЧИСЛЕНИЯ ПРЕОБРАЗОВАНИЯ ФУРЬЕ КОМПЛЕКСНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ

Пусть z(n) = x(n) + y(n)i - комплексная Т-периодическая последовательность, Z(m) — спектр Фурье:

т-1

Z(m) = zE^n)®™, (m = 0,1,...,Т-1, й) = ехр{27%}, Т = 51).                 (14)

п=0

Предложен ие 31 - Для вычисления Z(m) достаточно М(Т) вещественных умножений, где

М(Т) = —Tlog Т + О(Т).(15)

Доказательство . Представим Z(m) в форме:

%-14

Z(m) = Zz(n)a>5™ + Zz. Ы«“, n=0а=1

где

Ze(m) = ^ z(5n + a)co5mn = 22za(n)o>5mn.                                       U6)

n=0                   n=0

Для вычисления Zjm) образуем матричную последовательность периода Т/5 с коэффициентами из J:

< h(n) >=

< z1(n)> где < z$(n) >=(x$(n),y$(n))

^ z3(n)xz4(n)>J’

Для вычисления кодов матричного спектра <Н(т)> последовательности достаточно, согласно предложению 2.1, к,/т) 56        Л

М — = —Т log. Т - 2

<57 25 1 5      1

вещественных умножений. Далее, реконструкция Za(m) и Z(m) проводится по следующей схеме.

Шаг 1. Решая систему уравнений (3) для каждого ш, находим

a(m)>= 2>_a(n), п=0

что требует умножений только на степени двойки, которые мы не учитываем при анализе вычислительной сложности алгоритма.

Шаг 2. По известным кодам < Н_а(т) > находим <Н_а(т)>_а и <Н_а(т)>_р, что требует 8Т/5 вещественных умножений.

Шаг 3. В соответствии с предложением 1.5, имеем из (17);

И;1

С<н (mf^C-^ ^z/nl^W™,                          (18)

n=0

а в соответствии с предложением 1.10, из (17) имеем:

T£i

FaF"'= £W™.

n=0

Поэтому для

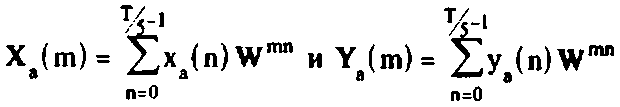
справедливы равенства:

2X(m)-Y(m)=C С *+Fa(dm)> F"¹, а            а                  а р                    а a

V5Y(m) = C С*¹ - F < H“(dm) > F~‘. а                 а р                   а' ’ a

Отметим, что для нахождения левых частей равенств (18), (19) и решения системы (20) достаточно О(Т) умножений.

Шаг 4. Окончательная реконструкция Z (ш) и Z(m), как нетрудно проверить, сводится к вычислениям по формулам:

Z (m) = е X (т)е^ + ie.Y (т)е^ а               1 а 1         2 a^v ' 2

и (16) ( здесь в) = (1,0), е2 =(0,1) — вектор—строки; т — знак транспонирования ).

Таким образом, суммируя вышесказанное, для мультипликативной сложности М(Т) вычисления Z(m) имеем рекуррентное соотношение:

М(Т) = М^ + ||т(1о85Т-2) + О(Т), откуда следует оценка (15).

• 4.    БЫСТРЫЙ АЛГОРИТМ ВЫЧИСЛЕНИЯ ПРЕОБРАЗОВАНИЯ ФУРЬЕ ВЕЩЕСТВЕННОЙ ПОСЛЕДОВАТЕЛЬНОСТИ

Пусть f(n) - вещественная входная Т-периодическая последовательность, F(m) -спектр Фурье.

Предложение—4.1. Для вычисления F(m) достаточно М^Т) вещественных умножений, где

M1(T) = -Tlog5T + O(T).

Доказательство . Представим F(m) в форме:

%-124

F(m) = Zfh^+EFjm^^ n=0a=l где

%-■%"

F(m) = ^f(25n+ а)тИтп = £га(п)оИт".

n=0n=0

Для вычисления F (m) образуем три матричные последовательности периода N/25 с коэффициентами из J:

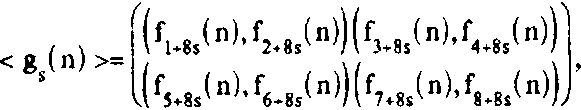
(s = 0,1,2)

понимая компоненты матриц < gs(n) > как элементы кольца J.

Производя вычисления матричных спектров и выделяя, как в предыдущем разделе, "частичные спектры" Fa(m), получаем в этом случае для М((Т)

рекуррентное соотношение:

Г 56 /

Т-з) +О(Т),

М,(Т) = М — + 3—Т log 1        <257   <125      5

откуда следует (21).

ЗАКЛЮЧЕНИЕ

Отмстим ряд характерных особенностей предложенной методики синтеза БПФ с совмещением в матричных кольцах.

Для рассмотренного случая (N = 5k, (2 х 2)-матрицы ) основные идеи алгоритма реализуются в наиболее рафинированном виде. Их экстраполяция на общий случай N = рк (р — простое число) возможна при наличии тождеств со значительным числом "тривиальных*' коэффициентов для матриц мультипликативного порядка р, аналогичных В. В частности, возможен синтез аналогичного алгоритма для р = 7 с совмещением в 30

кольце (3x3) — матриц, для которого С = — в оценке (1), что тоже несколько лучше 7

оценки, приведенной в [2]. Нахождение таких тождеств (или доказательство их отсутствия) представляет собой весьма трудную математическую задачу, связанную с тонкими арифметическими свойствами значений базисных функций дискретного преобразования Фурье как элементов поля алгебраических чисел.