Новый алгоритм количественного анализа в мёссбауэровской спектроскопии

Мёссбауэровская спектроскопия является неразрушающим ядерно-физическим методом анализа вещества. Важным достоинством метода является абсолютная селективность к выбранному изотопу, который играет роль высокочувствительного ядерного зонда, позволяя получать информацию о его локальном окружении [1–4]. Практическое применение мёссбауэровской спектроскопии в аналитических целях, как правило, ограничивается качественным анализом, т. е. решением задачи идентификации фаз или состояний резонансных атомов в различных неэквивалентных положениях (локально неоднородная система), входящих в состав анализируемого объекта. Основу качественного анализа составляет определение параметров сверхтонких взаимодействий (СТВ), соответствующих этим неэквивалентным положениям из экспериментальных мёссбауэровских спектров. С математической точки зрения эта процедура достаточно хорошо разработана для случаев статических СТВ [5, 6], т. е. когда изменения СТВ (флуктуации) не меняются за время жизни мёссбауэровского ядра в возбужденном состоянии (~10–7 с).

Наибольшую трудность с методической точки зрения представляет задача определения содержания мёссбауэровских атомов (или резонансных ядер этих атомов), находящихся в том или ином локальном окружении. Получение количественной информации в большинстве случаев ограничивается определением относительной доли резонансных атомов в том или ином локальном окружении, фактически это означает определение площади под соответствующими компонентами спектра. При этом оговаривается, что доля этих атомов определена с точностью до фактора Лэмба— Мёссбауэра f. Данный параметр зависит от колебательных свойств резонансных атомов в решетке и является масштабным множителем, влияющим на величину аналитического сигнала в спектре. Основная проблема проведения количественного анализа связана с необходимостью учета в теоретической модели взаимодействия мёссбауэровского излучения с реальными объектами как фундаментальных, так и эмпирических параметров, отражающих особенности рассматриваемого метода.

В работе [7] нами были предложены способы определения этих параметров и основанный на этих способах алгоритм проведения количест-

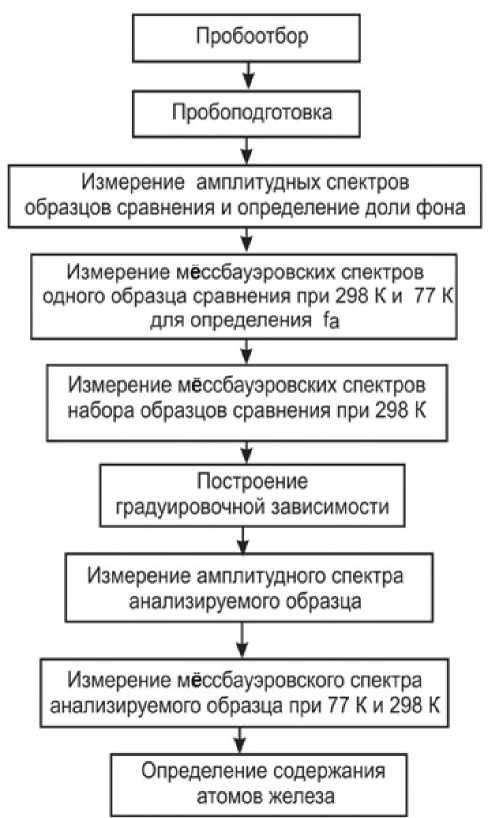
Рис. 1. Алгоритм проведения количественного анализа с использованием построения градуировочного графика венного анализа в мёссбауэровской спектроскопии.

Применения данных процедур можно избежать при использовании градуировочного графика, измеренного с помощью стандартных образцов (СО). Наиболее предпочтительными СО являются образцы с известным содержанием определяемого элемента, находящегося в том же локальном окружении, что и анализируемый элемент. Однако в реальных условиях получение таких образцов является достаточно трудоемкой задачей.

В настоящей работе для построения градуировочной зависимости предлагается использовать легкодоступные эталоны. Например, фольги металлического железа различных толщин для анализа содержания железа в фольгах или ферроциа- нид калия (K4[Fe(CN)6]*3H2O) для анализа порошкообразных проб. Основной трудностью применения подобных стандартных образцов является определение факторов Лэмба—Мёссбауэра для резонансных атомов, находящихся как в стандартных, так и в анализируемых образцах.

АЛГОРИТМ ПРОВЕДЕНИЯ КОЛИЧЕСТВЕННОГО АНАЛИЗА

На рис. 1 приведен алгоритм анализа с использованием градуировочного графика, построенного с использованием стандартных эталонов.

В отличие от предложенного в работе [7] алгоритма, здесь добавляется этап построения градуировочной зависимости. Для этого проводятся измерения амплитудных и мёссбауэровских спектров серии стандартных образцов с различным содержанием резонансных атомов ( С ст ) при тех же условиях, при которых планируется измерение анализируемого образца.

На следующем этапе производится нормировка серии измеренных мёссбауэровских спектров с учетом доли фоновой составляющей. Выражение для нормировки спектра имеет следующий вид:

_{N '( v )} = N ( v ) - b ⋅ N ( ∞ )

N ( ∞ ) ⋅ (1 - b )

где N’(v) — нормированный мёссбауэровский спектр; N(v) — измеренный мёссбауэровский спектр; N(∞) — число импульсов мёссбауэровского спектра вдали от резонанса; b — доля фоновой составляющей, определенная как отношение площади всех нерезонансных импульсов к общей площади амплитудного спектра в пределах установленной области измерения мёссбауэровского спектра (между нижним и верхним порогами дискриминатора).

Из нормированных мёссбауэровских спектров определяются площади под спектральными линиями ( S ). Затем строится градуировочная зависимость в координатах S от произведения концентрации резонансных атомов, находящихся в стандартном образце, выраженной в мг/см², на их фактор Лэмба—Мёссбауэра ( C ст · f ст ).

На рис. 2 в качестве примера представлена градуировочная зависимость для ферроцианида калия, фактор Лэмба—Мёссбауэра которого составил 0.478 ± 0.005.

На заключительной стадии анализа измеряются амплитудные и мёссбауэровские спектры анализируемого образца при двух различных температурах. После нормировки мёссбауэровских спектров с учетом фоновой составляющей производится разложение спектра на отдельные компоненты, соответствующие различным окружениям

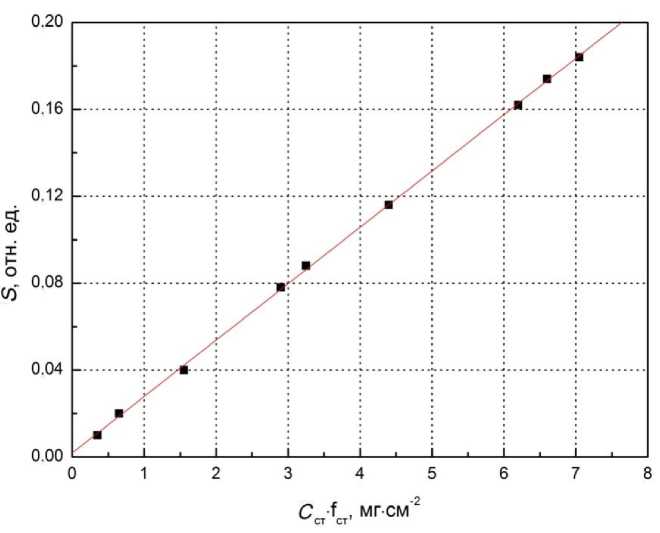
Рис. 2. Градуировочная зависимость, построенная с использованием ферроцианида калия

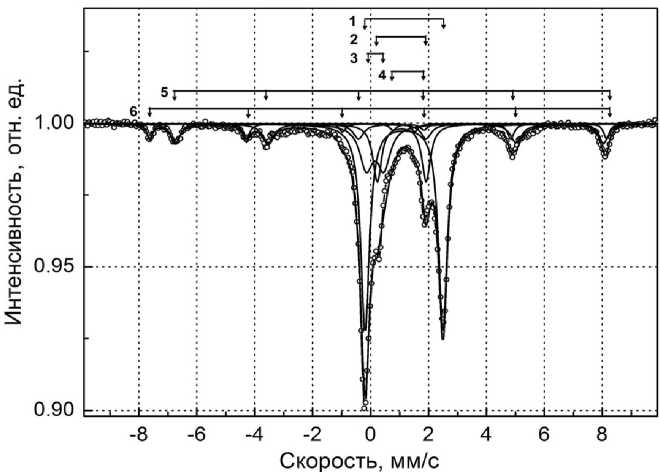
Рис. 3. Мёссбауэровский спектр железной руды, измеренный при Т = = 300 К, и результат его разложения на отдельные подспектры, соответствующие атомам железа в различных окружениях (фазах).

• 1    — Fe(II); 2 — Fe’(II); 3 — Fe(III);

• 4    — Fe”(II); 5, 6 — Fe 3 O 4

резонансных атомов, определение их площадей ( S i ) и факторов Лэмба—Мёссбауэра (f i ).

По градуировочному графику определяется произведение C a i · f i . Окончательное значение концентрации вычисляется делением этого произведения на фактор f i .

Разработанный алгоритм был апробирован на примере определения количественного содержания железа, находящегося в различных неэквивалентных окружениях в образце силикатной же- лезной руды. В соответствии с алгоритмом, изложенным в работе [8], выбирались оптимальные толщины образцов для исключения искажения формы спектральных линий. Качественный анализ, с помощью мёссбауэровской спектроскопии заключался в разложении мёссбауэровского спектра на отдельные подспектры, отвечающие различным химическим окружениям атомов железа (рис. 3).

Табл. 1. Результаты количественного анализа с использованием градуировочного графика

№	Состояние Fe		С а , % ( n = 4, p = 0.95) ± 0.1
1		Fe(II)	13.2
2		Fe’(II)	3.2
3		Fe(III)	2.3
4		Fe”(II)	0.9
5	(Fe 3 O 4 )	Fe(II) Fe(III)	0.9 3.1

Табл. 2. Результаты химического анализа и данные, полученные методом мёссбауэровской спектроскопии

Состояние атомов Fe	Титриметрия	Мёссбауэровская спектроскопия
		без использования образцов сравнения		градуировочная зависимость
	С а , % ( n = 4, p = 0.95)	C a , % ( n = 4, p = 0.95)	Δ, %	C a , % ( n = 4, p = 0.95)	Δ, %
e общ	24.0 ±0.1	21 ±1	10.6	23.6 ±0.4	1.8
Fe(II)	18.5 ±0.1	15.9 ±0.8	12.4	18.2 ±0.4	2.0

По мёссбауэровским параметрам, полученным для соответствующих подспектров, были идентифицированы следующие железосодержащие фазы: магнетит Fe 3 O 4 , оливин, лепидокрокит γ-FeOOH.

В табл. 1 приведены результаты количественного анализа железной руды с использованием предложенного подхода. Концентрации атомов железа даны в массовых процентах от общей массы навески.

Для проверки правильности полученных результатов анализа был проведен анализ исследуемой руды титриметрическими методами: бихроматометрическим определением содержания желе-за(II) и пермангонатометрическим определением валового содержания железа. Разложение пробы осуществляли в смеси соляной и плавиковой кислот при нагревании.

В табл. 2 приводится сравнение результатов титриметрического анализа с результатами мёссбауэровской спектроскопии, полученными без использования образцов сравнения по алгоритму из работы [7] и с помощью градуировочной зависимости. В таблице Δ — относительное отклонение результатов анализа мёссбауэровской спектроскопии от результатов титриметрического анализа.

Из таблицы видно, что способ с применением градуировочной зависимости дает более близкие результаты к химическому анализу по сравнению со способом без использования стандартных об- разцов. Занижение результатов анализа в последнем случае может быть связано с недостаточно высокой точностью определения параметров источника и неучтенным в расчетах влиянием дисперсности анализируемого образца.

ЗАКЛЮЧЕНИЕ

Для проведения количественного анализа в мёссбауэровской спектроскопии предложено использование стандартных образцов с идентичной по отношению к анализируемому образцу матрицей.

Этот подход заключается в построении градуировочной зависимости аналитического сигнала от концентрации резонансных атомов с помощью легкодоступных образцов сравнения, отличающихся по составу от анализируемых образцов.

Для практической реализации предложенного подхода разработан алгоритм проведения анализа, который был проверен при анализе реального объекта. Показано, что подход, основанный на применении градуировочной зависимости, является менее трудоемким в экспериментальном плане и более экспрессным. Он дает более точные результаты анализа по сравнению с предложенным ранее способом без использования образцов сравнения.