Новый метод группировки переменных для задач параметрической оптимизации большой размерности

Автор: Вахнин А.В., Сопов Е.А.

Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau

Рубрика: Информатика, вычислительная техника и управление

Статья в выпуске: 3 т.19, 2018 года.

Бесплатный доступ

Сложность и размерность прикладных задач глобальной параметрической оптимизации стремительно увеличиваются с каждым годом. Стоит отметить, что практические задачи оптимизации являются слож- ными и зачастую рассматриваются как модель «черного ящика» по причине того, что исчерпывающий анализ проблемы затруднен или невозможен, а частичная информация о проблеме редко является полезной. Эффек- тивным инструментом для решения задач оптимизации типа «черный ящик» являются эвристические алгоритмы прямого поиска. В последние десятилетия исследователи разработали множество эвристических алгоритмов для решения задач глобальной оптимизации большой размерности. Предложен новый подход, который получил название DECC-RAG. Алгоритм DECC-RAG базируется на ори- гинальном методе группировки переменных (случайная адаптивная группировка) для применения метода кооперативной коэволюции. В основе предложенного метода группировки переменных лежит следующая идея: после заданного количества вычислений целевой функции, применяя структуру кооперативной коэволюции для алгоритма SaNSDE, находится половина субкомпонентов с худшими значениями пригодностей, в данных суб- компонентах происходит случайное перемешивание индексов переменных. Эффективность алгоритма DECC-RAG проверялась на 20 эталонных тестовых задачах из набора LSGO CEC’2010 и 15 задачах из набора LSGO CEC’2013. Размерность задач равнялась 1000. Результаты численных экспериментов показывают, что предложенный алгоритм (DECC-RAG) превосходит некоторые другие со- временные эволюционные алгоритмы на задачах глобальной оптимизации большой размерности из LSGO CEC’2010 и LSGO CEC’2013.

Еще

Оптимизация, большая размерность, эволюционные алгоритмы, кооперативная коэволюция

Короткий адрес: https://sciup.org/148321849

IDR: 148321849 | DOI: 10.31772/2587-6066-2018-19-3-386-395

Текст научной статьи Новый метод группировки переменных для задач параметрической оптимизации большой размерности

Введение. Прикладные задачи глобальной оптимизации с каждым годом становятся все сложнее. Большинство реальных задач оптимизации имеют большую размерность. Данный тип задач сложен для решения по ряду причин: пространство поиска увеличивается экспоненциально по мере увеличения количества переменных, свойства пространства поиска могут меняться, зачастую стоимость оценки решения высока. В 2002 году NASA опубликовало статью [1], где были продемонстрированы тенденции роста размерности реальных задач глобальной оптимизации. Если раньше большая размерность в задачах глобальной оптимизации означала пару десятков переменных, то сегодня их более тысячи. Существует множество проблем глобальной оптимизации большой размерности из разных областей [2–5]: datamining, инженерия, нейроинформатика, химия и др. Стоит обратить внимание на то, что большинство реальных задач оптимизации относятся к типу «черный ящик» (Black-Box (BB)). Особенность данного типа задач заключается в том, что мы не имеем информации о свойствах решаемой задачи, которые могут быть использованы при поиске глобального экстремума, мы можем получить только значения целевой функции f ( X ) для точки X из пространства поиска. При решении задач типа «черный ящик» свою эффективность продемонстрировали эволюционные алгоритмы (ЭА) [6; 7].

Классическая задача оптимизации в общем случае может быть сформулирована следующим образом [8]:

f (X ) = f (Xi, x 2,..., Xn )^ min/^max,(1)

XL < X,-< XU, i =1, n ,(2)

gj ( Xi, X 2,..., Xn )< 0, j = 1, m ,(3)

hk (Xi,X2,...,Xn ) = 0,k = 1,l.(4)

В уравнении (1) f обозначает целевую функцию, X является допустимым множеством решений, n – целое число, обозначающее размерность задачи оптимизации. В уравнении (2) x_i ^L и x_i ^U обозначают нижнюю и верхнюю границу интервала поиска соответственно. Уравнения (3) и (4) обозначают ограничения типа неравенства и равенства соответственно. В данной статье рассматриваются задачи безусловной оптимизации, на которые не накладываются ограничения типа (3) и (4).

Задачи глобальной параметрической оптимизации моделей типа «черный ящик», в которых число переменных равно 1000 и более, принято называть задачами глобальной оптимизации большой размерности (Large-Scale Global Optimization (LSGO)). В [9] пока- зано, что наилучшие результаты для задач LSGO достигаются в классе бионических алгоритмов прямого поиска. В частности, высокую эффективность демонстрируют различные эволюционные алгоритмы.

Подходы к решению задачи LSGO на основе эволюционных алгоритмов

1. Дифференциальная эволюция (Differential Evolution). Storn и Price представили оригинальный подход для параметрической оптимизации в 1995 году, он получил название Differential Evolution (DE) [10]. DE является разновидностью эволюционного алгоритма, поэтому в ходе его работы используется итерационная процедура, которая состоит из повторяющегося применения операторов мутации, скрещивания, селекции. Более детально с данным алгоритмом можно ознакомиться в [11].
2. Самонастраивающаяся дифференциальная эволюция с поиском в окрестности (Self-adaptive differential evolution with neighborhood search (SaNSDE)). SaNSDE – самонастраивающаяся дифференциальная эволюция с поиском в окрестности [12]. На основе классического алгоритма DE в 2008 году была предложена его модификация. Данный алгоритм был выбран по той причине, что в нем присутствует самонастройка его параметров в ходе работы. Это очень важно, так как эффективность работы любого ЭА напрямую зависит от выбранных параметров. Для DE основными параметрами являются тип мутации, F , CR . F – параметр, характеризующий максимально возможное расстояние, на которое может расшириться область поиска оптимума по одной переменной за один шаг эволюции. Зачастую значения параметра F находятся в интервале [0; 2]. CR – параметр, отвечающий за частоту скрещивания: чем выше его значение, тем больше переменных решения будут замещены новыми мутантными значениями, значения CR находятся в интервале [0; 1]. Особенность алгоритма SaNSDE заключается в том, что алгоритм фиксирует успешное и неуспешное применение того или иного типа мутации, значения параметров F , CR , после определенного количества поколений пересчитывает вероятность выбора типа мутации, значения CR и значения F .
3. Кооперативная коэволюция (Cooperative Coevolution) . Одним из наиболее известных и часто применяемых подходов для решения задач большой размерности является декомпозиция на основе метода кооперативной коэволюции.

Кооперативная коэволюция (Cooperative Coevolution (CC)) является эволюционной структурой (рис. 1), которая делит вектор задачи оптимизации на несколько субкомпонентов и оптимизирует их независимо с помощью ЭА (до момента кооперации) для решения задачи оптимизации. Впервые данный метод предложили Potter и De Jong [13] применительно к генетическому алгоритму. CC на сегодняшний день является эффективным инструментом при решении сепарабельных задач оптимизации большой размерности. Ниже представлен псевдокод кооперативной коэволюции:

Псевдокод кооперативной коэволюции

1: Произвести декомпозицию целевого вектора на m субкомпонентов меньшей размерности ;
2: Присвоить i = 1 и начать новый цикл ;
3: Оптимизировать i-ю субкомпоненту с помощью ЭА ;
4: Если i < m, i = i+1 и перейти к шагу 3, иначе к шаг 5 ;
5: Остановить алгоритм, если условие остановки выполнено, иначе перейти к шагу 2 для следующего цикла.

Стоит заметить, что на сегодняшний день существует множество подходов, направленных на решение задач оптимизации большой размерности. Данные подходы можно разделить на две группы: подходы с использованием CC и подходы, не использующие декомпозицию вектора решения. Большую эффективность имеют те методы, которые используют CC для решения задачи оптимизации. При использовании CC появляются следующие новые задачи: выбор количества субкомпонентов (на сколько частей делить вектор решения), выбор размера каждой субкомпоненты и какие переменные объединять в одну группу. В связи с этим сегодня популярны следующие группировки, используемые в CC: группировка, где заранее задается условие, по которому происходит группировка (static grouping) [14], динамическая случайная группировка переменных (random dynamic grouping) [15], адаптивная группировка (learning dynamic grouping) [16], где проводится серия экспериментов по приращению значений каждой переменной, на основании полученных результатов переменные группируются.

DECC-RAG алгоритм. Сведения, изложенные выше, послужили основой для разработки нового ЭА для решения задач оптимизации большой размерности. Главная идея алгоритма заключается в использовании оригинального метода группировки переменных для эволюционной структуры CC с самонастраивающимся ЭА (SaNSDE). Самонастройка необходима, так как решаемая задача оптимизации представлена в виде модели «чёрный ящик», мы не знаем функциональной зависимости между переменными, следовательно, параметры должны адаптироваться во время работы алгоритма.

Подход CC является эффективным, но только в том случае, если правильно сгруппировать переменные. Было решено, что в основе метода группировки переменных должна присутствовать случайность, так как при использовании группировки типа learning dynamic grouping не всегда удается разделить переменные на истинное количество субкомпонент [16], но при этом будет затрачено большое количество ресурсов (вычисление функции пригодности) в ходе выделения субкомпонентов.

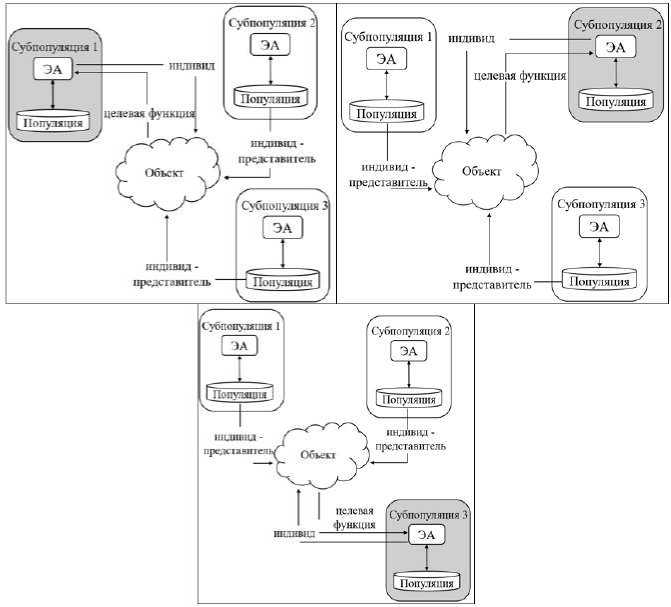
Рис. 1. Схематичное представление работы кооперативной коэволюции

Fig. 1. Schematic representation of cooperative coevolution

Помимо этого, может случиться так, что переменные сгруппируются верно, но оставшееся количество вычислений функции останется малым – внушительная часть бюджета вычислений уходит на группировку переменных. Количество группируемых переменных должно быть одинаковым для каждой субкомпоненты, данное решение было принято по причине того, что иначе придётся решать следующие дополнительные задачи:

1. Выбор различного количества индивидов. Например, для ЭА, оптимизирующего субкомпоненты вектора решения, состоящие из 5 переменных и 500 переменных, необходимо разное количество индивидов в популяции. Получается неравномерное распределение ресурсов алгоритма.
2. Минимальное и максимальное количество группируемых переменных. Как упоминалось неоднократно выше, задача глобальной оптимизации представлена в виде модели типа «чёрный ящик», т. е. неизвестно, какое значение выбирать в качестве минимального и максимального размера группы.

Предложенный оригинальный метод группировки Random Adaptive Grouping (RAG) работает следующим образом: D -мерный вектор решения разбивается на m s -мерных субкомпонент. Случайно, по равномерному закону распределения группируем переменные в одинаковые группы. Так как мы изначально не знаем, насколько хорошо себя показала та или иная группировка, необходимо провести определенное количество вычислений функции пригодности T (запустить работу ЭА на каждой субкомпоненте), после чего найти m/ 2 субкомпонент с худшими значениями функции пригодности индивидов-представителей, по равномерному закону распределения случайно перегруппировать переменные в данных группах. Далее нужно произвести сброс параметров ЭА в худших m/ 2 субкомпонентах после перегруппировки переменных, это делается из-за того, что после перегруппировки переменных конкретному ЭА необходимо будет уже решать совершенно другую задачу. Данный метод группировки переменных получил название RAG, а алгоритм, разработанный на его основе – DECC-RAG. Псевдокод алгоритма DECC-RAG представлен ниже:

Псевдокод алгоритма DECC-RAG

FEV_local и FEV_global – счетчики для оценки функции пригодности внутри адаптационного периода и для всего алгоритма соответственно. В нашем случае мы использовали следующие значения параметров алгоритма: NP = 50 (размер популяции для каждой субкомпоненты), m = 10, T = 3 х 10 5 . T – параметр, который представляет собой количество FEVs (оценок функций) перед случайным перемешиванием худших m/ 2 субкомпонент.

Описание эталонных тестовых задач и критериев оценки эффективности алгоритмов LSGO. Алгоритмы DE, SaNSDE и DECC-RAG тестировались на 20 тестовых функциях большой размерности из набора IEEE (The Institute of Electrical and Electronic Engineers) LSGO (Large-Scale Global Optimization) CEC’2010 (Congress on Evolutionary Computation) [17] и 15 тестовых функциях большой размерности из набора IEEE LSGO CEC’2013 [18]. Данные тестовые функции специально были наделены свойствами, которые присущи реальным задачам оптимизации большой размерности.

Полученные результаты работы алгоритмов (DE, SaNSDE, DECC-RAG) на задачах LSGO CEC’2010 и LSGO CEC’2013 сравнивали с результатами работы известных алгоритмов оптимизации (DMS-L-PSO [19], DECC-G [15], MLCC [20], DECC-DG [16]) для задач большой размерности. Результаты работы DMS-L-PSO, DECC-G, MLCC, DECC-DG на задачах из LSGO CEC’2010 и LSGO CEC’2013 были взяты из [21].

Для проведения экспериментов использовались правила соревнования LSGO CEC’2010 и LSGO CEC’2013, а именно:

– размерность тестовых задач оптимизации D = 1000;
– количество независимых запусков алгоритма для каждой тестовой задачи равно 25;
– количество вычислений функции пригодности в каждом независимом запуске 3 × 10⁶;
– после проведения 25 независимых запусков для тестовой функции вычисляется медианное значение (Median) и среднеквадратическое отклонение (Std).

Программная реализация алгоритмов (DE, SaNSDE и DECC-RAG) осуществлялась в среде разработки приложений Visual Studio – 2015 на языке программирования C++. В ходе проведения экспериментов значительное время тратится на вычисление функций пригодности. Тестирование алгоритмов проводилось с использованием параллельных вычислений с помощью технологии OpenMP.

Результаты численных экспериментов. В табл. 1, 2 приведено время (в секундах), затраченное на вычисление 10 000 раз данной тестовой функции на 1 потоке на процессоре AMD Ryzen 71700x. При проведении экспериментов использовался 16-поточный процессор для распараллеливания экспериментов – каждая тестовая функция вычислялась на отдельном потоке. Если не использовать данный прием, то только на разрешенное правилами конкурса количество вычислений функции пригодности в рамках данной работы потребовалось бы порядка 847,6 ч (35,5 дня).

В нашем случае время удалось сократить до 80,3 ч.

В табл. 3, 4 продемонстрированы результаты работы алгоритмов на тестовых функциях из набора LSGO CEC’2010 и LSGO CEC’2013 соответственно. Первый столбец обозначает номер тестовой функции, после- дующие столбцы – результаты работы того или иного алгоритма. В каждой ячейке таблицы содержатся два значения – медианное и среднеквадратическое отклонение, которые получены по результатам 25 независимых запусков.

Таблица 1

Время вычисления 10 000 функций пригодности в секундах на задачах из набора LSGO CEC’2010

Func. № Время	F1 0,396	F2 0,209	F3 0,21	F4 0,52	F5 0,334	F6 0,34	F7 0,309	F8 0,307	F9 1,312	F10 1,134
Func. №	F11	F12	F13	F14	F15	F16	F17	F18	F19	F20
Время	1,139	0,112	0,126	2,219	2,016	2,04	0,077	0,133	0,072	0,1

Таблица 2

Время вычисления 10 000 функций пригодности в секундах на задачах из набора LSGO CEC’2013

Func. № Время

F1 7,76

F2 8,08

8,1

F4 8,36

F5 8,76

F6 8,88

F7 3,19

F8 10,17

F9 10,59

F10 10,62

Func. №

F11

F12

F13

F14

F15

_–

Время

10,1

0,126

10,04

10,03

7,71

_–

Таблица 3

Результаты численных экспериментов алгоритмов на задачах (F1–F20) из набора LSGO CEC’2010, D = 1000

№ func

DECC-RAG

SaNSDE

DMS-L-PSO

DECC-G

MLCC

DECC-DG

2,69E-18

5,10E-18

4,19E+08

2,75E+08

2,00E+04

2,04E+06

1,61E+07

1,41E+06

3,53E-07

1,44E-07

1,66E-14

2,97E-12

1,42E+02

4,66E+04

7,33E+02

7,52E+01

7,38E+03

3,02E+02

2,80E+03

1,67E+02

5,53E+03

5,38E+02

1,32E+03

2,55E+01

2,43E+00

1,52E+00

4,46E+03

1,87E+02

1,64E+00

1,77E-01

1,95E+01

8,60E-02

1,47E+01

4,31E-01

1,56E+01

1,08E-01

1,14E+00

3,35E-01

6,24E-10

1,12E-06

1,66E+01

3,02E-01

9,50E+11

3,50E+11

8,78E+12

3,43E+12

2,82E+12

1,01E+12

4,32E+11

8,05E+10

2,46E+13

8,14E+12

1,78E+13

5,47E+12

5,08E+12

1,89E+12

1,54E+08

4,41E+07

7,96E+07

2,12E+07

9,00E+07

8,22E+06

9,35E+07

9,04E+06

2,50E+08

6,84E+07

5,11E+08

1,07E+08

1,52E+08

2,15E+07

2,04E+01

5,75E+06

2,09E+01

6,84E+06

1,27E+06

8,12E+05

3,66E+01

1,21E+01

4,71E+06

1,03E+06

1,97E+07

4,37E+06

1,64E+01

3,45E-01

2,90E+02

8,22E+02

3,08E+08

1,76E+08

1,90E+05

6,18E+04

3,47E+06

1,16E+05

6,57E+08

5,40E+08

1,15E+08

1,45E+08

9,20E+03

1,26E+04

1,78E+07

7,43E+08

2,53E+08

3,88E+08

8,16E+06

2,22E+07

2,02E+07

1,88E+06

9,06E+07

2,64E+07

8,82E+07

3,40E+07

1,62E+07

2,63E+07

6,17E+07

8,72E+06

5,56E+08

8,20E+07

2,31E+08

9,95E+07

2,08E+07

1,58E+06

4,35E+08

4,87E+07

2,48E+08

2,16E+07

5,52E+07

6,45E+06

F10

3,25E+03

1,88E+02

7,72E+03

2,47E+02

9,40E+03

2,82E+02

5,09E+03

4,26E+02

1,02E+04

3,13E+02

3,97E+03

1,45E+03

4,47E+03

1,29E+02

F11

2,16E+02

1,31E+01

1,88E+02

6,40E+00

1,74E+02

1,51E+01

1,68E+02

1,90E+00

2,59E+01

1,73E+00

1,98E+02

1,12E+00

1,02E+01

8,71E-01

F12

8,88E+03

1,15E+03

5,59E+05

6,91E+04

4,03E+05

4,83E+04

2,83E+01

9,88E+00

9,69E+04

9,55E+03

1,01E+05

1,57E+04

2,58E+03

1,08E+03

F13

1,56E+03

3,81E+03

1,01E+09

6,79E+08

2,52E+04

1,61E+05

1,03E+05

6,18E+04

4,59E+03

4,16E+03

2,12E+03

4,70E+03

5,06E+03

3,65E+03

F14

2,01E+08

2,07E+07

1,60E+09

1,52E+08

7,78E+08

1,28E+08

1,25E+07

1,62E+06

9,72E+08

7,52E+07

5,71E+08

5,50E+07

3,46E+08

2,42E+07

F15

5,16E+03

3,60E+02

7,75E+03

2,55E+02

1,06E+04

4,34E+02

5,48E+03

3,46E+02

1,24E+04

8,24E+02

8,67E+03

2,07E+03

5,86E+03 1,05E+02

F16

4,13E+02

3,05E+01

3,77E+02

4,32E+00

3,73E+02

1,12E+01

3,18E+02

2,04E+00

6,92E+01

6,43E+00

3,96E+02

5,76E+01

7,50E-13

6,25E-14

F17

1,68E+05

1,17E+04

1,04E+06

7,94E+04

8,68E+05

6,84E+04

4,75E+01

1,15E+01

3,11E+05

2,24E+04

3,47E+05

3,11E+04

4,02E+04

2,29E+03

F18

4,96E+03

6,35E+03

4,15E+10

1,70E+10

5,83E+05

1,81E+08

2,50E+04

1,10E+04

3,54E+04

1,53E+04

1,59E+04

9,48E+03

1,47E+10

2,03E+09

F19

2,23E+06

1,93E+05

2,96E+06

4,01E+05

1,93E+06

1,89E+05

2,03E+06

1,41E+05

1,14E+06

6,23E+04

2,04E+06

1,42E+05

1,75E+06

1,10E+05

F20

1,84E+03

5,04E+02

5,25E+10

1,58E+10

2,80E+05

1,37E+07

9,82E+02

1,40E+01

4,34E+03

8,25E+02

2,27E+03

2,26E+02

6,53E+10

6,97E+09

Таблица 4

Результаты численных экспериментов алгоритмов на задачах (F1-F15) из набора LSGO CEC’2013 , D = 1000

№ func

DECC-RAG

SaNSDE

DMS-L-PSO

DECC-G

MLCC

DECC-DG

1,88E-16

3,11E-16

5,28E+08

2,92E+08

8,53E+05

8,25E+06

1,97E+09

1,27E+08

2,06E-06

4,27E-06

9,07E-14

4,38E-09

6,03E+02

1,81E+04

1,40E+03

1,39E+02

2,46E+04

1,72E+03

2,06E+04

8,50E+02

8,61E+03

4,88E+02

1,30E+03

3,63E+01

3,57E+00

1,73E+00

1,28E+04

7,20E+02

2,03E+01

2,33E-02

2,16E+01 6,07E-03

2,10E+01

8,05E-02

2,08E+01

1,66E-01

2,02E+01

6,18E-03

2,00E+01

2,76E-04

2,14E+01

1,45E-02

1,11E+10

7,50E+09

1,11E+11

3,43E+10

2,93E+10

1,13E+10

2,97E+11

7,25E+10

2,00E+11

1,22E+11

1,99E+11

1,26E+11

7,33E+10

2,82E+10

3,50E+06

7,09E+05

4,62E+06

7,57E+05

4,88E+06

5,29E+05

3,92E+06

5,82E+05

8,44E+06

1,14E+06

1,17E+07

3,46E+06

5,81E+06

3,83E+05

1,06E+06

8,62E+02

1,06E+06

1,36E+03

1,06E+06

1,34E+03

9,98E+05

5,20E+03

1,06E+06

1,84E+03

1,05E+06

4,13E+03

1,06E+06

1,07E+03

2,40E+08

3,68E+08

1,04E+09

6,95E+08

2,20E+08

1,88E+08

1,22E+09

7,64E+08

1,04E+09

4,48E+08

1,15E+09

1,07E+09

4,25E+08

1,92E+08

4,76E+14

1,89E+14

2,15E+15 1,04E+15

2,26E+14

1,32E+14

1,68E+14

5,09E+14

7,90E+15

3,18E+15

8,18E+15

6,18E+15

2,89E+15

1,85E+15

2,32E+08

5,21E+07

4,27E+08

6,45E+07

4,81E+08

4,69E+07

3,50E+08

4,61E+07

5,86E+08

9,76E+07

8,85E+08

2,92E+08

4,95E+08

3,18E+07

F10

9,42E+07

5,91E+05

9,42E+07

1,85E+05

9,40E+07

2,51E+05

9,11E+07

1,06E+06

9,30E+07

6,16E+05

9,27E+07

6,07E+05

9,45E+07

2,46E+05

F11

3,45E+09

6,42E+10

2,50E+11

1,95E+11

3,18E+09

1,12E+10

9,44E+10

7,53E+10

1,26E+11

7,15E+10

1,90E+11

1,53E+11

3,81E+10

4,33E+10

F12

1,82E+03

3,85E+02

4,64E+10

1,61E+10

1,49E+07

3,79E+08

5,22E+04

5,52E+04

4,19E+03

7,83E+02

2,36E+03

7,51E+02

1,68E+11

2,24E+10

F13

7,19E+09

4,77E+09

1,52E+10

4,47E+09

6,92E+09

3,15E+09

1,32E+10

6,58E+09

8,67E+09

2,78E+09

9,94E+09

3,73E+09

2,08E+10

5,53E+09

F14

3,80E+10

6,70E+10

3,42E+11

1,54E+11

5,27E+10

3,39E+10

2,21E+11

1,26E+11

1,28E+11

5,86E+10

2,06E+11

8,54E+10

1,56E+10

1,44E+10

F15

1,59E+07

4,50E+07

7,32E+09

2,13E+11

6,12E+07

4,13E+07

1,54E+07

3,45E+06

1,13E+07

1,26E+06

1,57E+07

1,90E+06

9,52E+06

2,30E+06

Произведем попарное сравнение независимых выборок (лучших найденных значений в 25 независимых запусках), используя критерий Уилкоксона – непараметрический статистический тест, используемый для проверки статистических различий между двумя независимыми выборками. В табл. 5, 6 занесены результаты теста статистической значимости различий между результатами работы алгоритмов DECC-RAG vs DE и DECC-RAG vs SaNSDE на тестовых функциях из набора LSGO CEC’2010 соответственно. В табл. 7, 8 занесены результаты теста на статистическую значимость различий между результатами работы алгоритмов DECC-RAG vs DE и DECC-RAG vs SaNSDE на тестовых функциях из набора LSGO CEC’2013 соответственно. Если в соответствующей ячейке (табл. 5–8) стоит знак «+», то это означает, что результаты работы алгоритмов статистически различны и лучшее найденное медианное решение – у первого алгоритма, если стоит знак «–», то это означает, что результаты работы алгоритмов статистически различны и лучшее найденное медианное решение – у второго алгоритма, если стоит знак «≈» – результаты работы алгоритмов статистически не различаются на данной тестовой функции.

На рис. 2–4 продемонстрированы графики, на которых отражены усредненные результаты работы алгоритмов DE, SaNSDE и DECC-RAG на некоторых

(1, 2, 9, 12, 14, 18) тестовых функциях из набора LSGO CEC’2010: по оси абсцисс – количество вычислений функции пригодности, по оси ординат – среднее значение функции пригодности. На рис. 5 и 6 продемонстрированы результаты работы алгоритмов DE, SaNSDE и DECC-RAG на некоторых тестовых функциях (1, 2, 3, 12) из набора LSGO CEC’2013. На рис. 7 и 8 в виде столбчатых диаграмм отображен средний ранг алгоритмов по всем тестовым функциям из эталонных наборов LSGO CEC’2010 и LSGO CEC’2013 соответственно. Ранг вычислялся по медианным результатам из табл. 3 и 4 в зависимости от места, которое занял алгоритм на той или иной функции: чем меньше медианное значение, тем меньше значение ранга. На двух эталонных наборах предложенный алгоритм DECC-RAG имеет наименьший средний ранг.

Анализируя полученные численные результаты работы алгоритма DECC-RAG (рис. 7, 8), можно заключить, что он превосходит некоторые известные алгоритмы глобальной оптимизации большой размерности (DMS-L-PSO, DECC-G, MLCC, DECC-DG) на 20 эталонных тестовых функциях из набора LSGO CEC’2010 и 15 эталонных функциях из набора LSGO CEC’2013.

Статистической значимости различий между результатами работы алгоритмов не наблюдается на F6 из LSGO CEC’2010 у DECC-RAG vs SaNSDE, на F6 у DECC-RAG vs DE и на F7, F10, F11 из LSGO CEC’2013.

На всех остальных тестовых функциях наблюдает ся статистическая значимость различий между ре зультатами работы алгоритмов.

Статистическая значимость работы алгоритмов (DECC-RAG vs DE) на 20 тестовых функциях LSGO CEC’2010

Таблица 5

F 1 +	F 2 +	F 3 +	F 4 +	F 5 _–	F 6 +	F 7 +	F 8 +	F 9 +	F 10 +
F 11	F 12	F 13	F 14	F 15	F 16	F 17	F 18	F 19	^F20
_–	+	+	+	+	+	+	+	+	+

Статистическая значимость работы алгоритмов (DECC-RAG vs SaNSDE) на 20 тестовых функциях LSGO CEC’2010

Таблица 6

F 1 +	F 2 +	F 3 +	F 4 +	F 5 _–	F 6	F 7 +	F 8 _–	F 9 +	F 10 +
F 11	F 12	F 13	F 14	F 15	F 16	F 17	F 18	F 19	F 20
+	+	+	+	+	_–	+	+	_–	+

Статистическая значимость работы алгоритмов (DECC-RAG vs DE) на 15 тестовых функциях LSGO CEC’2013

Таблица 7

F 1 +

F 2 +

F 3 +

F 4 +

F 5 +

F 6

F 7 +

F 8 +

F 9 +

F 10 +

F 11 +

F 12 +

F 13 +

F 14 +

F 15 +

_–

Статистическая значимость работы алгоритмов (DECC-RAG vs SaNSDE) на 15 тестовых функциях LSGO CEC’2013

Таблица 8

F 1 +	F 2 +	F 3 +	F 4 +	F 5 +	F 6 +	F 7	F 8 _–
F 9	F 10	F 11	F 12	F 13	F 14	F 15	_–
+	≈	≈	+	_–	+	+	_–

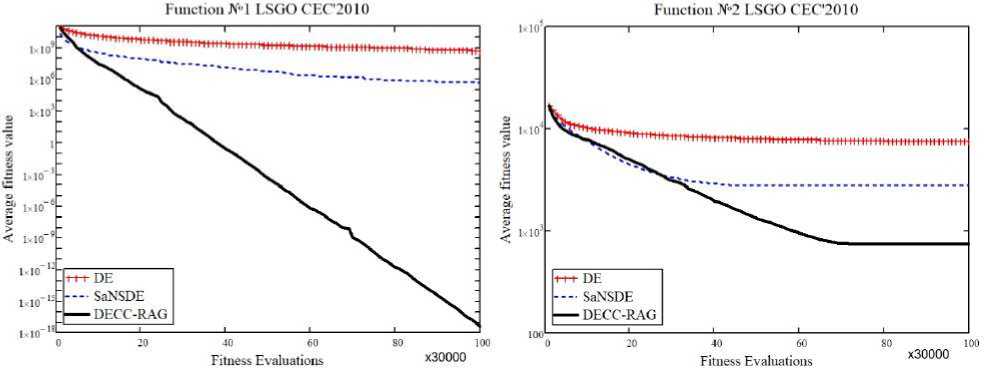
Рис. 2. Сходимость DE, SaNSDE и DECC-RAG на задачах (№ 1, 2) из набора LSGO CEC’2010

Fig. 2. The convergence graphs of DE, SaNSDE and DECC-RAG applied to F 1 , F 2 from LSGO CEC’2010

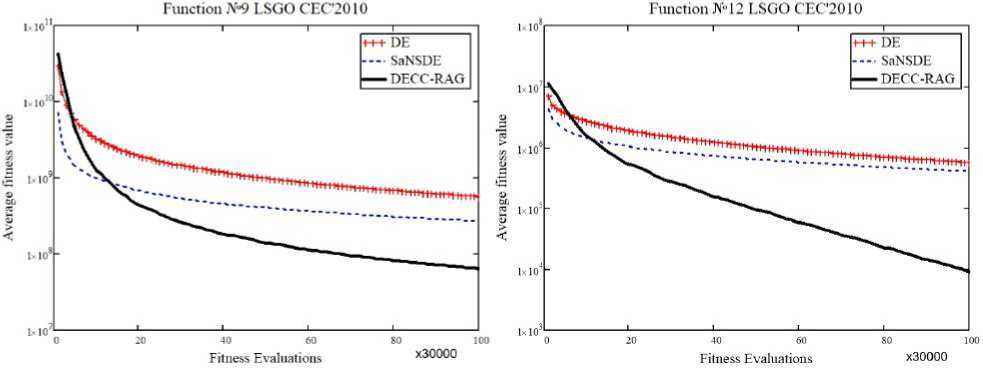
Рис. 3. Сходимость DE, SaNSDE и DECC-RAG на задачах (№ 9, 12) из набора LSGO CEC’2010

Fig. 3. The convergence graphs of DE, SaNSDE and DECC-RAG applied to F 9 , F 12 from LSGO CEC’2010

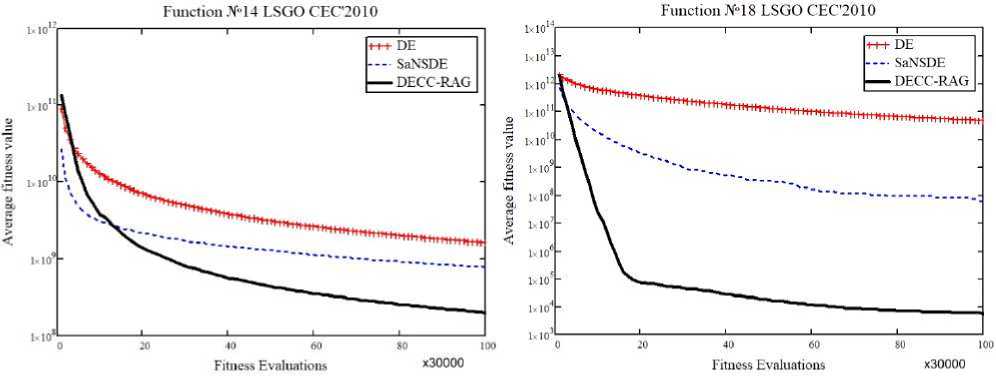
Рис. 4. Сходимость DE, SaNSDE и DECC-RAG на задачах (№ 14, 18) из набора LSGO CEC’2010

Fig. 4. The convergence graphs of DE, SaNSDE and DECC-RAG applied to F14, F18 from LSGO CEC’2010

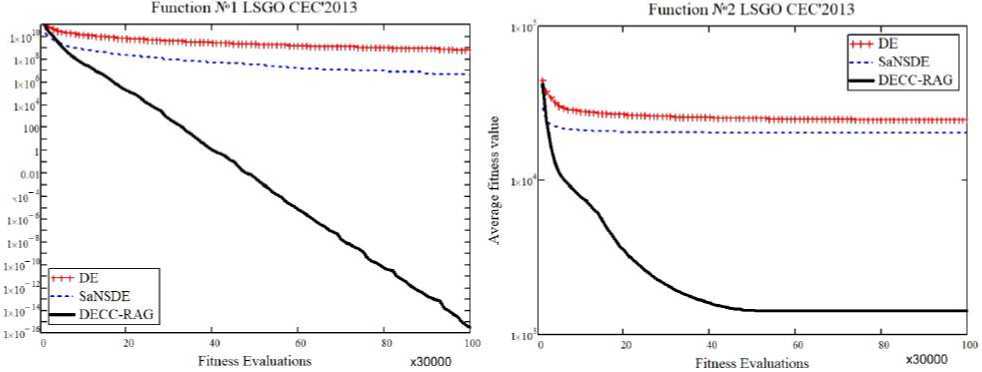
Рис. 5. Сходимость DE, SaNSDE и DECC-RAG на задачах (№ 1, 2) из набора LSGO CEC’2013

Fig. 5. The convergence graphs of DE, SaNSDE and DECC-RAG applied to F 1 , F 2 from LSGO CEC’2013

Average fitness value

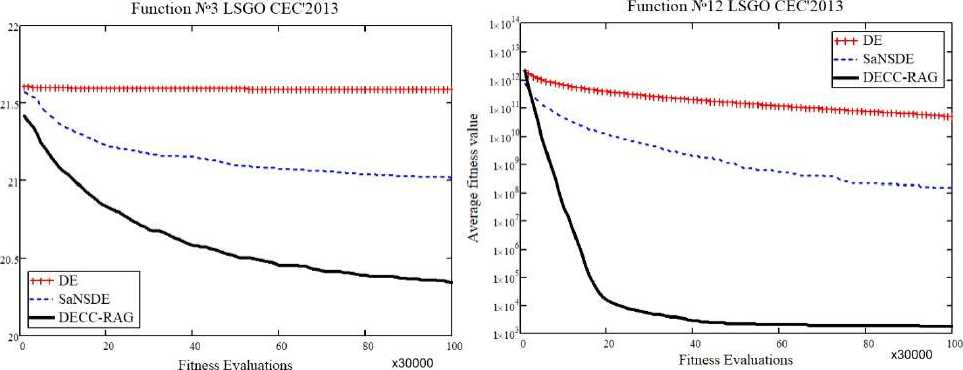
Рис. 6. Сходимость DE, SaNSDE и DECC-RAG на задачах (№ 3, 12) из набора LSGO CEC’2013

Fig. 6. The convergence graphs of DE, SaNSDE and DECC-RAG applied to F3, F12 from LSGO CEC’2013

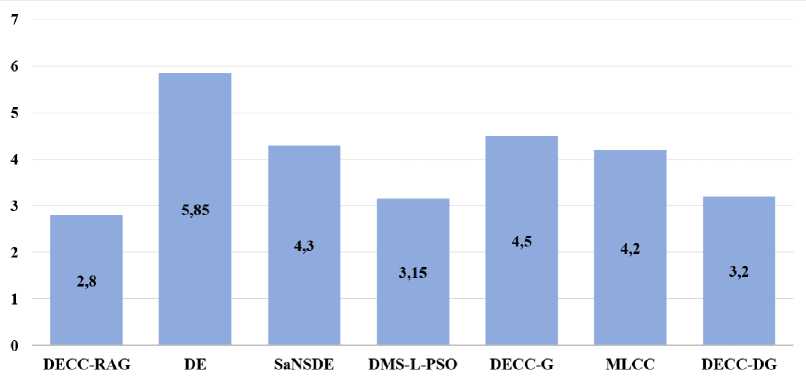
Рис. 7. Средний ранг алгоритмов на LSGO CEC’2010

Fig. 7. Average rank of algorithms on LSGO CEC’2010

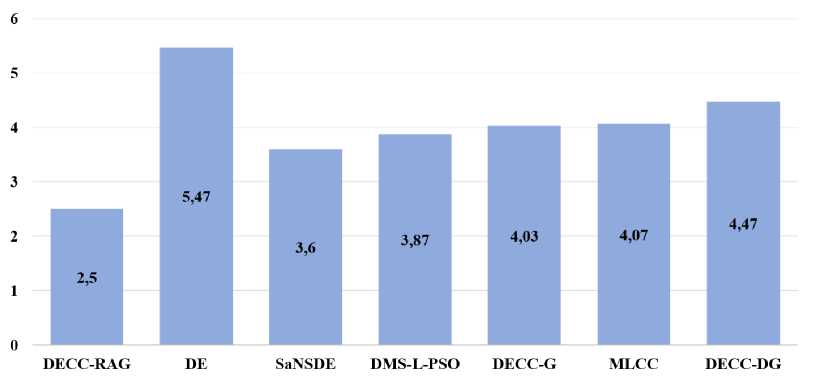
Рис. 8. Средний ранг алгоритмов на LSGO CEC’2013

Fig. 8. Average rank of algorithms on LSGO CEC’2013

Заключение. В данной статье предлагается новый эволюционный алгоритм, названный DECC-RAG, для задач глобальной оптимизации большой размерности. В основе предложенного алгоритма лежит случайная адаптивная группировка переменных для структуры кооперативной коэволюции. В качестве ЭА, который оптимизирует каждую субкомпоненту, мы применили эффективный самонастраивающийся эволюционный алгоритм SaNSDE.

Тестирование эффективности DECC-RAG проводилось на эталонных задачах из наборов LSGO CEC’2010 и LSGO CEC’2013. Алгоритм DECC-RAG превзошел некоторые известные алгоритмы, которые специально разрабатывались для задач глобальной оптимизации большой размерности. В дальнейших работах будет ставиться вопрос об улучшении эффективности предложенного алгоритма DECC-RAG для задач глобальной оптимизации большой размерности.

Acknowledgments. This work was supported by the Ministry of Education and Science of Russian Federation, № 2.1676.2017/ПЧ.

Список литературы Новый метод группировки переменных для задач параметрической оптимизации большой размерности

Vanderplaats G. N. Very large scale optimization. National Aeronautics and Space Administration (NASA), Langley Research Center. 2002, 55 p.
Shuhei Kimura, Kaori Ide, Aiko Kashihara, Makoto Kano, Mariko Hatakeyama, Ryoji Masui, Noriko Nakagawa, Shigeyuki Yokoyama, Seiki Kuramitsu, Akihiko Kona- gaya. Inference of s-system models of genetic networks using a cooperative coevolutionary algorithm. Bioinformatics (Oxford, England). 2005, Vol. 21, Iss. 7, P. 1154-1163.
Wei-Po Lee, Yu-Ting Hsiao. Inferring gene regulatory networks using a hybrid ga-pso approach with numerical constraints and network decomposition. Information Sciences. 2012, Vol. 188, P. 80-99.
Bo Jiang, Ning Wang, Cooperative bare-bone particle swarm optimization for data clustering. Soft Computing. 2014, Vol. 18, Iss. 6, P. 1079-1091.
Lin Lin, Mitsuo Gen, Yan Liang. A hybrid EA for high-dimensional subspace clustering problem. Proceedings of the 2014 IEEE Congress on Evolutionary Computation, CEC 2014. 2014, P. 2855-2860.

Статья научная