Новый метод описания изменения траектории оси лазерного пучка в дифференциальной кювете Андерсона для определения показателя преломления жидких сред

В современном мире постоянно увеличивается количество негативных факторов, которые влияют на состояние окружающей среды, что приводит к отклонениям от стандартного состояния во многих конденсированных средах [1 – 3]. С другой стороны, повышение цен на энергоносители и многие виды услуг приводит к снижению качества выпускаемой продукции [4, 5]. Поэтому большое внимание в данной ситуации уделяется методам и приборам для контроля состояния конденсированных сред. Одной из важных составляющих в системе контроля конденсированных сред является экс-пресс-контроль в реальном времени [1, 3, 6 – 8]. Его роль в мире постоянно возрастает. Для контроля состояния различных конденсированных сред, особенно биологических и медицинских суспензий, кислот и прочих, требуется высокая точность изме- рений [1, 3, 8, 9]. Необходимо также отметить, что прибор для экспресс-контроля должен обладать широкими функциональными возможностями по применению (обеспечить контроль параметров большого числа сред) и не вносить необратимых изменений в состояние среды [1, 3, 8 – 10]. В настоящее время многофункциональный экспресс-контроль можно реализовать только с использованием явления ядерного магнитного резонанса (ЯМР) и рефракции [1 – 3, 5, 8, 9, 11 – 15]. В отличие от ЯМР-измерений рефракция нашла намного больше практических приложений в решении различных задач на основе определения значения показателя преломления [14 –20] по причине компактности измерительных приборов и оперативности получения результата.

Одним из перспективных приборов для реализации данных измерений является рефрактометр с дифференциальной кюветой Андерсона [10, 14,

20 – 22]. Это единственный тип рефрактометра, который позволяет проводить измерения опасных и летучих жидких сред в объеме с высокой степенью герметичности (поворотная крышка с прокладкой для дифференциальной кюветы). Необходимость в таких измерениях с увеличением числа опасных сред, а также с увеличением продолжительных по времени исследований летучих сред в мире постоянно возрастает.

В монографии [21] подробно рассмотрены различные типы дифференциальных рефрактометров и принципы измерения показателей преломления n m в этих приборах и различные математические соотношения для определения n m с использованием приближений. Эти приближения позволяют получить в дифференциальных рефрактометрах погрешность измерения n m не лучше 0,01. Измерения n m с такой точностью не удовлетворяют современным требованиям для исследований и контроля состояния сред. Это привело к тому, что производство дифференциальных рефрактометров было прекращено.

Основной проблемой при разработке конструкции рефрактометра с дифференциальной кюветой Андерсона в отличие от других рефрактометров является отсутствие уравнения без любых приближений для определения зависимости изменения показателя преломления n m исследуемой среды от параметров кюветы, от показателя преломления n s эталонной жидкости, а также особенностей регистрации положения оси лазерного излучения на фотодиодной линейке. Это не позволяет определить оптимальные соотношения между параметрами кюветы, значением n s и расстоянием l от стенки кюветы до фотодиодной линейки для обеспечения погрешности измерения n m порядка 10 ^–4 с учетом допусков на изготовление граней и перегородки дифференциальной кюветы Андерсона из кварцевого стекла или других материалов.

Поэтому целью нашей работы является вывод уравнения для описания изменения траектории оси лазерного пучка от источника лазерного излучения до сенсоров фотодиодной линейки. Данное уравнение должно позволить получить аналитическое решение для n m относительно параметров процесса его измерения, которые можно изменять в конструкции рефрактометра. Это позволит определить критические значения для оптической системы рефрактометра, соответствующие максимуму отношения сигнал/шум регистрируемого лазерного излучения и обеспечить минимальную погрешность измерения n m . А также используя это соотношение для расчета погрешности косвенных измерений, определить влияние допусков по размерам при изготовлении граней и перегородки кюветы на значение погрешности определения n m . Это обстоятельство является ключевым при аттестации промышленного прибора (дифференциального рефрактометра) по погрешности измерения n m .

Уравнение траектории оси лазерного пучка в дифференциальной кювете Андерсона и за её пределами до фотодиодной линейки

Для вывода уравнения траектории рассмотрим схему оптической части дифференциального рефрактометра, в которой происходит изменение оси траектории лазерного излучения. На рис. 1 представлена схема дифференциальной кюветы Андерсона и направление распространения оси траектории лазерного излучения в ней и до фотодиодной линейки 4.

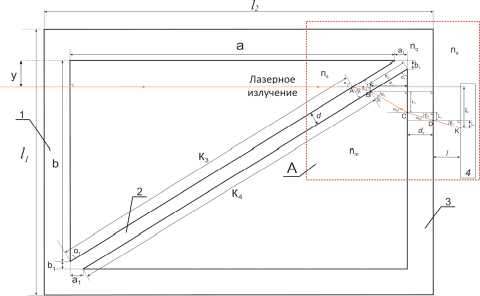
Рис. 1. Дифференциальная кювета Андерсона с направлением распространения оси лазерного излучения:

1 – боковая грань кюветы Андерсона, на которую поступает лазерное излучение; 2 – перегородка;

3 – боковая грань кюветы Андерсона, через которую выходит лазерное излучение; 4 – фотодиодная линейка

Для примера на рис. 2 представлена одна из конструкций дифференциальной кюветы Андерсона (вид сверху) с геометрическими размерами (толщина перегородки d =3 мм, толщина стенки кюветы d 1 =3 мм, внешние размеры кюветы l 1 =70 мм, l 2 =50 мм, внутренние размеры кюветы а + а 1 = 64 мм, b + b 1 =44 мм).

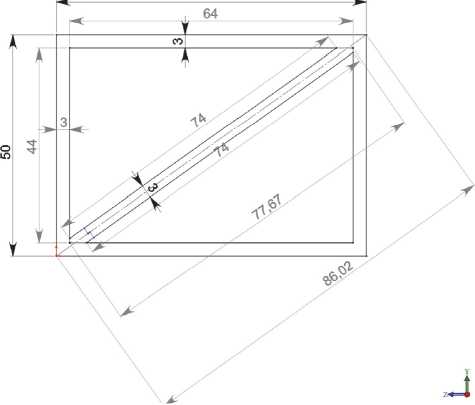
Рис. 2. Дифференциальная кювета Андерсона (вид сверху) с размерами (рис. 1) в мм

На рис. 3 представлена 3D-модель варианта дифференциальной кюветы Андерсона (рис. 2).

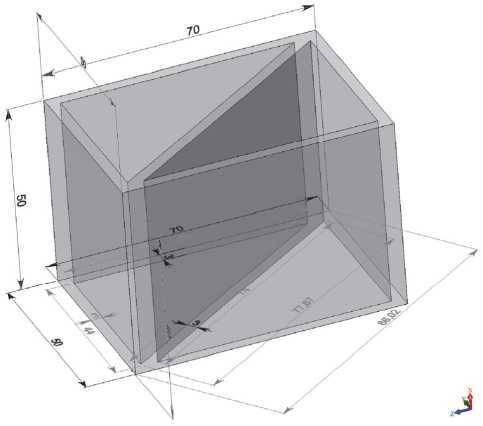
Рис. 3. 3D-модель варианта дифференциальной кюветы Андерсона с размерами в мм

На рис. 4 представлена кювета с термопарой для контроля температуры Т .

Рис. 4. Фото дифференциальной кюветы Андерсона с термопарой

Для контроля температуры Т в двух частях кюветы Андерсона используют две термопары. Классическая конструкция термопары представлена на рис. 4 (сверху кюветы). Погрешность определения температуры Т составляет 0,1 К.

Изменения в траектории распространения лазерного излучения происходит в выделенном фрагменте А на рис. 1. Поэтому рассмотрим подробно процессы, происходящие в этой части траектории оси лазерного излучения. На рис. 5 представлен фрагмент А (рис. 1).

Перед выводом уравнения для описания изменения положения оси лазерного излучения при прохождении его через дифференциальную кювету с жидкими средами и расстояния l до фотодиодной линейки 4 (рис. 5) определим следующее. Геометрически – лучевой подход для описания изменения оси лазерного излучения рассматривается нами, когда жидкие среды прозрачны, однородны, искажения в плоском волновом фронте лазерного излучения минимальны.

В случае присутствия в исследуемой среде различных частиц, которые вызовут рассеяние лазерного излучения, например, Ми, искажения в форме пучка будут значительные и однозначно определить положение оси лазерного излучения на фотодиодной линейке будет крайне сложно.

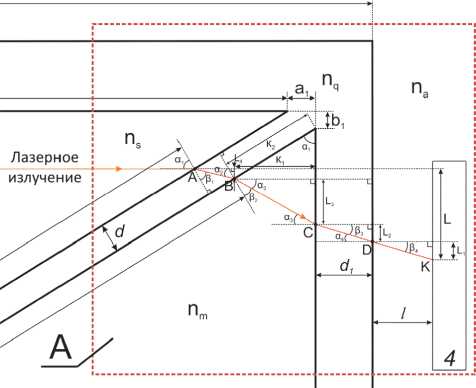
Рис. 5. Фрагмент А с частью дифференциальной кюветы Андерсона, фотодиодной линейкой 4 и промежутком с расстоянием l между стенкой кюветы и фотодиодной линейкой

Структура формирования траектории оси лазерного излучения от 1 до 4 основана на его преломлении на границах нескольких сред с различными показателями преломления в точках А, B , C и D (рис. 1 и 5). Рассматриваются смещения по вертикали точек B , C , D и К (параллельно грани 1) относительно точки А (рис. 5). Для каждого смещения (расстояния L 1 , L 2 , L 3 и L 4 ) выводится математическое соотношение с учетом параметров кюветы (геометрических размеров, материала и т.д.), значений показателей преломления эталонной n s и исследуемой n m среды, места ввода лазерного излучения в кювету (грань 1 – точка О – расстояние y (рис. 1)) и расстояния l до фотодиодной линейки 4.

При проведении исследований жидких сред с использованием рефрактометра с дифференциальной кюветой Андерсона могут возникнуть три ситуации (nm > nq, nm = nq и nm < nq), где nq – показатель преломления кварца (материал, из которого изготовлена кювета). Эти ситуации в таком контексте ранее никто не рассматривал по причине того, что в уравнениях для описания оси траектории лазерного излучения не учитывалась толщина перегородки d кюветы и материал, из которого она изготовлена [14, 21]. Соотношения между показателями преломления материала, из которого изготовлена кювета, перегородка кюветы и жидких сред необходимо учитывать, чтобы в процессе измерения на границе двух сред не возникло явление полного внутреннего отражения. В этом случае лазерное излучение может не поступить на сенсоры фотодиодной линейки и проводить измерения показателя преломления nm будет невозможно. Поэтому при выборе эталонной жидкости и конструкции кюветы Андерсона необходимо учитывать следующие соотношения:

sin(α 1 )· n s / n q <1,0, (1) sin(α 1 )· n s / n m <1,0. (2)

Эти соотношения ранее при проведении исследований с использованием дифференциального рефрактометра не рассматривали. При изменении дискретности шкалы измерения показателя преломления n m эти соотношения внесут коррективы в выбор эталонной жидкости и размеров кюветы Андерсона.

Кроме кварца, для изготовления кювет можно использовать сапфир и различные стекла КУ, КФ и т.д. Выбор кюветы будет определяться решаемыми задачами при исследованиях. В этом случае при вычислениях в полученном соотношении для определения n m , вместо показателя преломления кварца, используется показатель преломления материала, из которого изготовлена кювета.

Траектория изменения оси лазерного излучения представлена на рис. 1 и 5. Для определения смещения оси траектории L относительно первоначального положения ввода лазерного излучения в кювету Андерсона нами было выведено соотношение. Соотношение для L было сформировано из рассмотрения смещения оси лазерного излучения на 4 участках: L = L 1 + L 2 + L 3 + L 4 (рис. 5). При выводе соотношения для L учитывалось наличие перегородки в кювете с параметрами d и n q , что ранее никто не делал.

Для фрагмента А (рис. 5) запишем следующие соотношения:

. sin a. n„ _ sin a₂ n_m A :----¹ = —; В :----² = —;

sin P i     ns sin p ₂     nq

C: sin a ₃ = nq ^ . sin a ₄ = na sin P 3 nm sin P 4 nq ’

a i a - +P 2 , L i = l ■ tg P 4 ,

L 2 = d i tg P - , L = Kitg a - ,

a

K i = ( У - b i + L 4 ) tg a i , tg a i = -,                     (5)

b

L ₄ = AS | ■ sin( a _i - P i ) =

= —-—sin( a _i - P i ) = d (sin a _i - cos a _i tg P , ), cos p _i

sin a _i sin p _i

nq              ns

= —^ sin p _i = — sin a _i ,

nn sq

_        ns sin ai tg в = /2  2'2

J n q - n 2 sin² a _i

Соотношения (3) – (7) в дальнейшем позволяют выразить значения L 1 , L 2 , L 3 и L 4 через параметры кюветы Андерсона, расстояние l , а также значения показателей преломления эталонной n s и исследуемой n m жидкой среды. В статье для воспроизведения результата вывода кратко представлены основные промежуточные соотношения.

L ₄ = d sin a _i i -

ns cos a _i

^nq - ns ² sin² a _i

tg a - = tg ( a i -P 2 ) =

tg a i - tg P 2 i + tg a i tg P 2 ,

sin a _i _ nq . sin a ₂ _ nm .

sin pi    ns  sin P2    nq sin ai   nm              ns .

a2 = P, ^----= — ^ sin p2 = — sin a sin P2   ns             nm

ns

— sin a_i            .

nm = ns sin a i

L n_s ² . ₂        nn2 - n_s ² sin² ai

. i - — sin2 a,   v m s i nm

ns sin ai tg ai - /       . =         /-------:----

L₃                   Jn- - ns ² sin² a _i sin a _i Jnm - ns ² sin² a _i - ns sin a _i cos a _i

--= tg a - =---------------:--------=---------.        . ==-------------

K i           i ₊ tg a _i      ns ^{sin a} i           cos a _i ^n^ - ns ² sin² a _i + ns sin² a _i

^1 nm - ns sin² a _i

tg в з = L ²

d ₁

sin a i

( nm - ns sin² a _i

- ns cos a _i

nq - sin² a _i ( nm + ns cos² a _i - ns sin² a _i - 2 ns cos a _i ^/ nm - ns sin² a i

L i = l ■ tg P 4

sin a₃ n„ sin a₄ n_a        „     sin a₃

---- = —; ---⁴ = —; a ₄ =p ₃ ^--- 3 sin P 3 nm sin P 4 nq               sin P 4

nanm

= — ^ sin p ₄ = — sin a ₃ ,

nm

na

■ _   sin ai/r^— 2 2

sin a3 =------1 ^/nm - n2 sin2 ai - ns cos ai nm

. _ sin a _i sin p₄ =------

na

( д/ nm - ns sin² a i - ns cos

sin a i

J = tg ₽ 4 =

na

(7 nm - ns ² sin² a _i - ns cos

1 -

sin a i

na

( <Щ

^^^^^^B

n ; sin² a i - ns cos

sin a i

(^ nm - ns sin² a i

- ns cos a i

/ n2 - sin² a i

nm - ns sin² a _i + ns cos² a _i - 2 ns cos a _i 4nm - ns ² sin² a _i

Далее с использованием всех рассмотренных ранее преобразований для определения смещения оси лазерного излучения на фотодиодной линейке L были получены соотношения для L 1 , L 2 , L 3 и L 4 . И получено общее соотношение для L .

(L = L + L2 + L3 + L4 = sin ai d i -I I

ns cos a i

4nq - ns sin² a _i

+

( 4nm - ns sin² a _i

- ns cos ai) x

l

/n2 - sin² a i

nm - ns sin² a _i + ns ² cos² a _i - 2 ns cos a _i 4nm - ns sin² a _i

+

d 1

+

nq - sin² a _i ( nm + ns cos² a _i - ns sin² a _i - 2 ns cos a _i ^nm - ns ² sin² a i

+

K 1

cos a _i 4nm, - ns ² sin² a _i + ns sin² a _i J^

Проведенные нами эксперименты показали, что для всех трех случаев ( n m >  n q , n m = n q и n m <  n q ) уравнение оси траектории L относительно первоначального положения ввода лазерного излучения в кювету Андерсона выводится одинаково. Только при выборе кюветы Андерсона и n s необходимо учитывать соотношения (1) и (2), чтобы обеспечить достоверность измерений n m .

Лабораторный макет дифференциального рефрактометра и результаты экспериментальных исследований

Для подтверждения адекватности полученного соотношения (8) был разработан лабораторный макет дифференциального рефрактометра. На рис. 6 представлена его структурная схема.

На рис. 7 представлен внешний вид лабораторного макета дифференциального рефрактометра на оптической плите.

Вся информация о различных изменениях в конструкции рефрактометра (параметры кюветы Андерсона и расстояния l ), а также об измеренном значении L поступает в компьютер, где осуществляется обработка и определение значения n m с использованием (8).

В качестве примера в табл. 1 представлены результаты исследования 50% водного раствора этанола (случай nm < nq). Это летучая среда, которая при исследованиях требует обеспечения герметичных условий, которые можно реализовать в дифференциальной кювете Андерсона с крышкой. Кроме того, было проведено сравнение результатов измерения nm с данными, полученными с использованием промышленного рефрактометра Аббе NAR – 2T (компания ATAGO, Japan) с погрешностью измерения 0,0002.

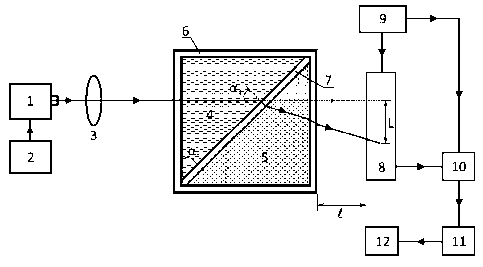
Рис. 6. Структурная схема дифференциального рефрактометра: 1 – полупроводниковый лазер, 2 – блок питания лазера; 3 – линза; 4 – эталонная жидкость;

5 – измеряемая жидкость; 6 – стенка кюветы Андерсона; 7 – перегородка между отсеками в кювете Андерсона;

8 – фотодиодная линейка; 9 – аналого-цифровой преобразователь; 10 – многофункциональный блок питания; 11 – устройство обработки; 12 – ноутбук

Для подтверждения адекватности вывода (8) и возможности его использования для других жидких сред были проведены с использованием разработанного лабораторного макета рефрактометра исследования изменения показателя преломления бензилового спирта и фенилгидразина. Данные жидкие среды выбраны для исследований неслучайно. При темпера- туре Т = 293,1 К значение показателя преломления бензилового спирта nm = 1,5397 ± 0,0002, что очень близко к значению nq = 1,5419 ± 0,0001 (кварца), из которого изготовлены кюветы Андерсона. Этот вариант исследования можно отнести к случаю nm = nq (температурная зависимость nq в пределах изменения Т от 273 до 300 К слабая). При определенной Т достигается соотношение nm = nq в пределах погрешности измерения, что отражено в табл. 2. В табл. 3 представлен случай nm > nq (исследуется изменение показателя преломления фенилгидразина от Т ). Необходимо отметить, что исследуемые среды также обладают повышенной летучестью и при длительном их исследовании необходим герметичный объем (кювета Андерсона с крышкой – идеальный вариант для данных исследований).

Рис. 7. Фото дифференциального рефрактометра

Табл. 1. Изменение показателя преломления n m 50 % водного раствора этанола от температуры Т

Т , К	Лабораторный макет дифференциального рефрактометра	Промышленный рефрактометр Аббе NAR – 2T
275,2 ± 0,1	1,3611 ± 0,0002	1,3610±0,0002
278,1 ±0,1	1,3609 ± 0,0002	1,3608±0,0002
283,1 ±0,1	1,3607 ± 0,0002	1,3605 ± 0,0002
287,3 ±0,1	1,3605 ± 0,0002	1,3602 ± 0,0002
290,2 ± 0,1	1,3603 ± 0,0002	1,3599 ± 0,0002
293,1 ±0,1	1,3592 ± 0,0002	1,3590 ± 0,0002
295,2 ± 0,1	1,3586 ± 0,0002	1,3583 ± 0,0002
300,2 ± 0,1	1,3571 ± 0,0002	1,3568 ± 0,0002
303,1 ±0,1	1,3559 ± 0,0002	1,3557 ± 0,0002
307,2 ± 0,1	1,3541 ± 0,0002	1,3539±0,0002
310,1 ±0,1	1,3527 ± 0,0002	1,3525 ± 0,0002
313,2 ± 0,1	1,3509 ± 0,0002	1,3506 ± 0,0002
316,2 ± 0,1	1,3486 ± 0,0002	1,3483 ± 0,0002

Анализ данных в табл. 1, 2 и 3 показывает, что результаты измерений n m , полученные на двух приборах, совпадают в пределах погрешности измерения, что подтверждает достоверность полученного нами соотношения (8) по результатам измерения L.

Погрешность определения nm с использованием (8) по результатам измерения L была оценена с использованием методики Матье, которая применяется в кванто- вых стандартах частоты. Было установлено, что погрешность измерения составляет значение порядка 0,0001. Методика Матье – это косвенная оценка, в которой разброс может составлять порядка 70% от полученного результата. Поэтому результаты измерения nm представляются в статье с погрешностью ± 0,0002.

Табл. 2. Изменение показателя преломления n m бензилового спирта от температуры Т

Т , К	Лабораторный макет дифференциального рефрактометра	Промышленный рефрактометр Аббе NAR – 2T
274,1 ±0,1	1,5422±0,0002	1,5421 ± 0,0002
278,0±0,1	1,5418±0,0002	1,5416 ± 0,0002
283,2±0,1	1,5414±0,0002	1,5413 ±0,0002
287,1 ±0,1	1,5409±0,0002	1,5408 ± 0,0002
290,1 ±0,1	1,5403±0,0002	1,5402 ± 0,0002
293,0±0,1	1,5397±0,0002	1,5396 ± 0,0002
295,1 ±0,1	1,5391 ±0,0002	1,5390 ± 0,0002
300,1 ±0,1	1,5378±0,0002	1,5377 ± 0,0002
303,2±0,1	1,5366±0,0002	1,5365 ± 0,0002
307,0±0,1	1,5340±0,0002	1,5339 ± 0,0002
310,2±0,1	1,5326±0,0002	1,5325 ± 0,0002
313,0±0,1	1,5309±0,0002	1,5308 ± 0,0002
316,2±0,1	1,5289±0,0002	1,5288 ± 0,0002

Табл. 3. Изменение показателя преломления n m фенилгидразина от температуры Т

Т , К	Лабораторный макет дифференциального рефрактометра	Промышленный рефрактометр Аббе NAR – 2T
275,1 ±0,1	1,6060±0,0002	1,6059±0,0002
278,2 ± 0,1	1,6062±0,0002	1,6061 ± 0,0002
283,0 ± 0,1	1,6065±0,0002	1,6064 ± 0,0002
287,1 ±0,1	1,6069 ± 0,0002	1,6068 ± 0,0002
290,0 ± 0,1	1,6073 ± 0,0002	1,6072 ± 0,0002
293,0 ± 0,1	1,6077 ± 0,0002	1,6076 ± 0,0002
295,1 ±0,1	1,6071 ± 0,0002	1,6070 ± 0,0002
300,1 ±0,1	1,6057 ± 0,0002	1,6056 ± 0,0002
303,2 ± 0,1	1,6044±0,0002	1,6043 ± 0,0002
307,0 ± 0,1	1,6028 ± 0,0002	1,6027± 0,0002
310,2 ± 0,1	1,6015±0,0002	1,6014 ± 0,0002
313,1 ±0,1	1,5999 ± 0,0002	1,5998 ± 0,0002
316,1 ±0,1	1,5985 ± 0,0002	1,5984 ± 0,0002

Для дополнительного подтверждения полученного соотношения (8) и функциональных возможностей разработанного лабораторного макета дифференциального рефрактометра была исследована водопроводная вода с различной степенью очистки. На рис. 8 в качестве примера представлены результаты этих исследований.

Анализ данных на рис. 8 показал, что результаты измерения значения n m , а также характер изменения зависимости n m от Т совпадает с результатами исследований, полученными другими учеными в работах [10, 14, 20, 22–28].

Результаты исследований показали, что для проведения измерений nm с погрешностью 0,0002 полученного нами соотношения (8) достаточно. Для обеспечения измерений значения nm с погрешностью ме- нее 0,0001 необходимо аналитическое соотношение для nm. Использование этого соотношения позволит управлять изменением дискретности шкалы измерения nm до шага 0,00001 и менее, изменяя параметры кюветы Андерсона, расстояние l и значение ns с учетом соотношений (1) и (2).

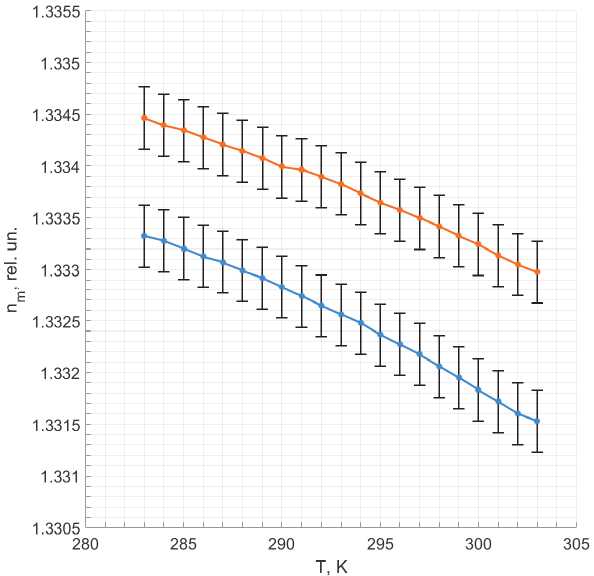
Рис. 8. Зависимость изменения величины показателя преломления n m от температуры Т для различных водных сред. График 1 соответствует фильтрованной водопроводной воде. График 2 соответствует водопроводной воде, содержащей оксиды железа

Заключение

Результаты проведенных исследований подтверждают адекватность предложенного нами метода для описания распространения оси лазерного излучения в кювете Андерсона и за её пределами до фотодиодной линейки. Выведенное соотношение (8) позволяет обеспечить с использованием разработанной нами конструкции малогабаритного дифференциального рефрактометра измерения показателя преломления n m жидких сред в диапазоне изменения от 1,2300 до 2,3300 с погрешностью 0,0002 при их экспресс-контроле в месте взятия пробы. Данной погрешности измерения достаточно для экспресс-контроля.

Полученное в результате рассмотрения распространения оси лазерного излучения до фотодиодной линейки соотношение (8) является новым результатом в данной области оптики, который дополняет раздел дифференциальных оптических систем новыми знаниями, так как в полной мере учитывает все процессы, которые оказывают влияние на изменение направления оси лазерного излучения в кювете Андерсона. Дальнейшее преобразование (8) в отличие от ранее применяемых соотношений в дифференциальных рефрактометрах с кюветой Андерсона [10, 14, 20, 21] может позволить получить аналитическое соотношение для nm для исследований влияния различных параметров кюветы Андерсона, а также значений ns и l на точность измерения nm при выполнении измерений в различных условиях. Использование нейронных сетей не может в полном объеме обеспечить адекватность данных исследований и определить пределы точности определения nm с использованием (8) в соответствии с допусками на изготовление граней кюветы и погрешностями определения l и ns.

Необходимо отметить, что дифференциальный рефрактометр с кюветой Андерсона является единственным прибором, который позволяет обеспечить длительное время полную герметичность пробы исследуемой среды (кювета Андерсона с поворотной крышкой и прокладками). Это необходимо при продолжительных исследованиях опасных сред (например, гептан, бензол и т.д.), спиртовых и биологических растворов, эфирных соединений, бензинов и т.д. Особенно при исследовании их температурных зависимостей в большом диапазоне изменения Т . Данные исследования отмеченных сред с обеспечением высокой точности измерения n m в других конструкциях промышленных рефрактометров сейчас реализовать крайне сложно.