Новый метод расчета кинетики процесса сушки тканей

Автор: Ольшанский А.И., Марущак А.С.

Журнал: Вестник Витебского государственного технологического университета @vestnik-vstu

Рубрика: Технология и оборудование легкой промышленности и машиностроения

Статья в выпуске: 1 (40), 2021 года.

Бесплатный доступ

Изложена новая методика расчета сушки тканей на основе уравнений кинетики сушки А.В. Лыкова и Г.К. Филоненко. Приведена обработка экспериментальных данных по конвективной и конвективно - радиационной сушке различных тканей. Даны уравнения для определения плотностей тепловых потоков, интенсивности испарения влаги, температуры для периода падающей скорости сушки. Представлены уравнения для определения длительности сушки тканей. Вычислены значения коэффициентов теплоотдачи и числа Био для различных тканей. Показано, что числа Био при сушке тканей меньше единицы, и основным лимитирующим фактором является внешний тепловлагообмен поверхности испарения влаги с поверхности материала с окружающей средой. Представлена проверка достоверности полученных расчетных уравнений и сопоставление расчетных значений с экспериментальными. Несовпадение значений находятся в допустимых пределах точности проведения и обработки эксперимента.

Еще

Влагосодержание, коэффициент теплопроводности, температура, сушка, коэффициент сушки, число био, плотность потока тепла, интенсивность испарения влаги, коэффициент теплоотдачи

Короткий адрес: https://sciup.org/142231209

IDR: 142231209 | DOI: 10.24412/2079-7958-2021-1-72-81

Текст научной статьи Новый метод расчета кинетики процесса сушки тканей

Витебский государственный технологический университет

Технология производства текстильных материалов характеризуется большим числом процессов, в которых сушка является необходимым процессом. Ткани после механического отжима в процессе сушки проходят целый ряд сложных

* E-mail: alexeymarushak@mail.ru (A. Marushchak) с 72

технологических операций, связанных с сушкой в технологической линии несколько раз, что связано со значительными затратами энергии на сушку [1, 2].

Совершенствование методов, обработки и сушки текстильных материалов связано с раз- работкой энергоэффективных сушильных материалов, с поиском новых химических реагентов, позволяющих сократить время обработки материала, выбора оптимальных гидродинамических режимов, разработки оптимальных температурных и тепловлажностных режимов сушки на каждой стадии технологического цикла [1-4]. В промышленности для сушки тканей широко используется конвективная и комбинированная сушки. Для расчета процесса сушки и контроля за качеством высушиваемого материала необходимы простые, надежные методы расчета с минимальным количеством констант, определяемых экспериментально [3, 4].

Цель исследования

На основе опытных данных по сушке тканей различными способами подвода тепла разработать простой, надежный метод расчета кинетики сушки для определения основных параметров тепловлагопереноса.

Кинетика сушки тканей

Ткани после механического отжима выходят с влагосодержанием й₀ = 1,1-1,3, и сушка предварительно обезвоженной ткани в отличие от большинства других тонких материалов сразу происходит в периоде убывающей скорости от начального влагосодержания и₀ и без периода постоянной температуры [4-7]. Связь между теплообменом и влагообменом устанавливается основным уравнением кинетики сушки А.В. Лыкова, которое при отсутствии периода постоянной скорости запишется [4, 7]:

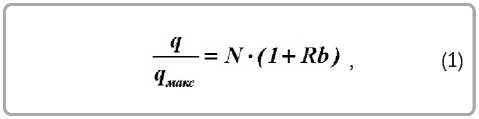
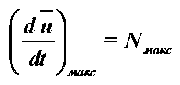
Число Ребиндера устанавливает связь теплообмена с влагообменом, и позволяет проводить расчет теплообмена по данным влагообмена без определения коэффициента теплоотдачи α [4, 5, 7].

При сушке тканей, как очень тонких материалов с толщиной δ ≈ 0,4 - 1,6 мм , расход тепла на нагревание влажного тела значительно меньше тепла на испарение из него влаги, и числом Rb << 1 и величиной Rb можно пренебречь [4, 6].

Для конвективной сушки балансовое уравнение тепла запишется в виде [4, 7]:

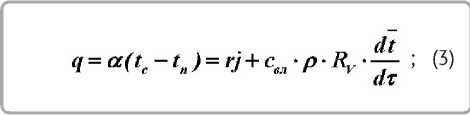
где а , Вт/м 2 • К - коэффициент теплоотдачи в периоде падающей скорости; t_n , ° C - температура на поверхности материала; r , кДж/кг – теплота парообразования; j , гр/м • с - интенсивность испарения влаги в периоде падающей скорости; с вл , кДж/кг • К - удельная теплоемкость влажного тела; R_V = V / F – отношение объема тела к поверхности; dt / d τ – скорость изменения температуры.

Пренебрегая вторым членом в правой части уравнения (3), можно записать для плотности потока тепла в периоде убывающей скорости сушки [4, 7, 8]:

где q , q_макс , Вт/м² – плотность потока тепла в периоде падающей скорости, максимальный тепловой поток.

, (4)

Относительная скорость сушки [3–5]:

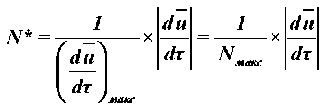
где j - интенсивность испарения влаги с поверхности материала в периоде убывающей скорости сушки.

Максимальная скорость сушки [4]:

Максимальная скорость сушки:

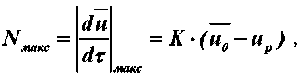
где K – коэффициент сушки [4]:

Максимальная плотность теплового потока:

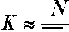
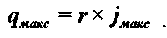
“о-“р где up – равновесное влагосодержание материала.

Подставляя в (2) скорость сушки из уравнения (5) с учетом (6) в первом приближении, получим выражение для относительной скорости сушки для периода убывающей скорости с погрешностью 7–10 %:

Текущие значения интенсивности испарения влаги и плотности тепловых потоков в первом периоде равны:

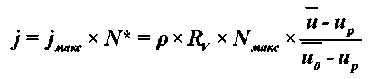
. (12)


H - и N^- __^ .	(7)
«₀-“p

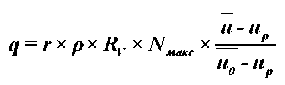
Из решения общего уравнения кривой скорости сушки | du / dτ | = N·N * Г.К. Филоненко [9] установил связь между теплообменом и влаго-обменом в виде уравнения:

t —t s.---- = N 6

где t_í и t_ñ – начальная температура и температура среды.

Из уравнений (7) и (8) находится температура на поверхности тканей для конвективной сушки:

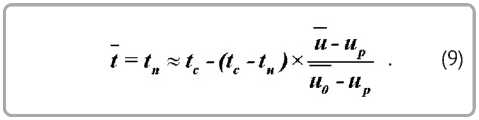
Температура t = t_ï , для тонких материалов, находится как среднеинтегральная для ткани.

Относительная скорость сушки N * не зависит от режима сушки и для конкретного материала при заданном методе сушки является лишь функцией влагосодержания [3, 4, 5].

Максимальная интенсивность испарения влаги с поверхности материала определяется по максимальной скорости сушки N_макс :

Плотность теплового потока по уравнению теплообмена Ньютона [4,7]:

q = a*(te-tH) , (14)

где коэффициент теплоотдачи α определяется по критериальному уравнению для теплообменного критерия Нуссельта [4, 7].

Обработкой экспериментальных данных по сушке многих различных материалов была установлена связь между относительной скоростью сушки N * и обобщенным временем Nτ [10]. При сушке материалов в периоде падающей скорости эта связь выражается уравнением [10]:

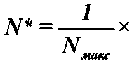
du dx

= exp(-axN_jHaKEx_T) , (15)

где N макс , %/ч – максимальная скорость сушки; τ , ( ñ )– время сушки от начального влагосодержа-ния u₀ . Константа а определяется приближенным соотношением [10]:

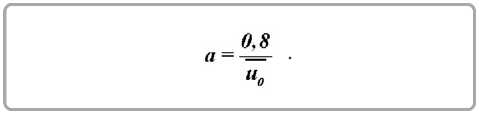
J лите Po ^ ^K ^ ^лмяс . (10)

Интегрируя уравнение (15), получим длительность процесса сушки [10]:

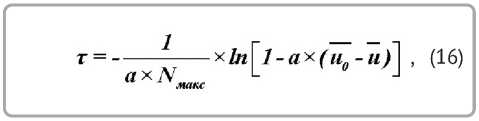
где а / (е вл ; p •R_V) - темп нагрева влажного тела при значениях числа Био Bi << 1 [6, 11].

Среднеинтегральная температура тканей из уравнения (22) равна:

где u - текущее влагосодержание материала.

Запишем уравнение (15) на основании (8):

. (23)

■х

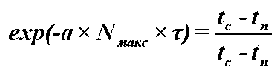
Темп нагрева тела m_t определяется экспериментально путем измерения температуры в любой точке тела для двух последовательных моментов времени регулярного режима [6, 11]:

Решением (17) определяется температура материала в процессе сушки:

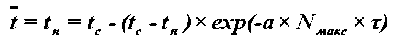
. (18)

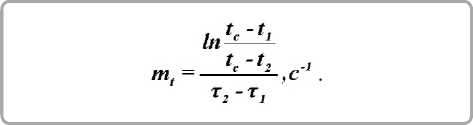
Запишем уравнение (15) на основании (7) в виде:

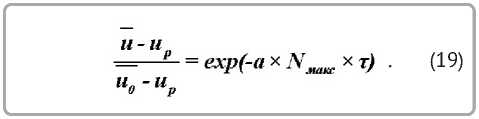
Длительность сушки тканей из решения (19):

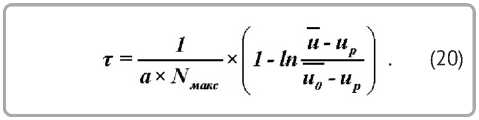
Секундный поток тепла на нагревание влажного тела по закону Ньютона [8]:

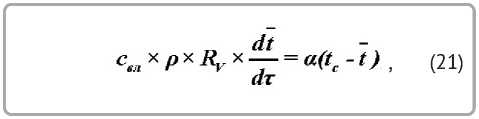
где dt / Д т - скорость нагрева тела, t - среднеинтегральная температура материала.

Запишем (21) и проинтегрируем [3, 8]

Текущие плотности тепловых потоков и интенсивность испарения влаги в периоде падающей скорости сушки при величине числа Ребиндера Rb ^ 0 определяются выражениями:

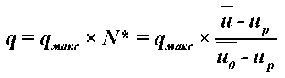
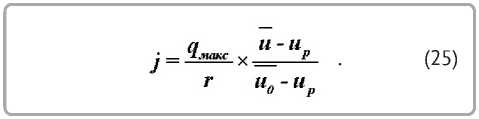
Теплота парообразования r определяется по таблицам [3].

Для вычисления числа Bi и проверки достоверности обработки опытных данных и точности полученных эмпирических уравнений для определения коэффициента теплоотдачи α использовалось уравнение для теплообменного числа Нуссельта [4–7]:

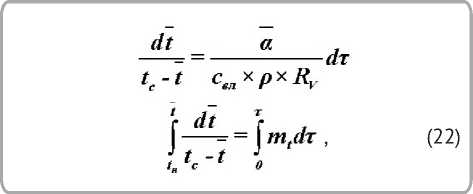
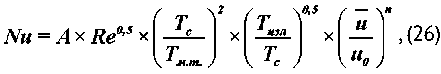
где Nu = al/Хеоз- критерий Нуссельта; Re = dl/ / vM3- критерий Рейнольдса; Тс, Тмт, Тию, К -абсолютные температуры среды, мокрого термометра, излучателя, l, м - длина материала по набеганию потока воздуха, Хвоз, Вт/м• К, νвоз, м2/с – коэффициенты теплопроводности и кинематической вязкости воздуха определялись по таблицам, ϑ, м/с – скорость воздуха. Отношение (u / u0)n – учитывает уменьшение коэффициента а с уменьшением влагосодер-жания ткани. Для сушки тканей коэффициент A = 0,89, постоянная n = 0,42 [4, 6]. Комплекс Òèçë / Òc учитывает увеличение коэффициента теплоотдачи а за счёт радиационного теплообмена.

Экспериментально установлено, что при радиационной сушке температура на поверхности материала за счёт излучения выше,чем при конвективной сушке при равных условиях сушки [4].

Число Био определяется соотношением:

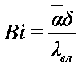
где δ , мм – толщина ткани.

Влияние температуры и влажности тканей на коэффициент теплопроводности тканей хорошо изучено [12, 13]:

Для шерстяных тканей λ _вл = λ ₀ + 0,0026 W .

Для льняной ткани λ _вл = λ ₀ + 0,0039 W ;

где λ ₀ – коэффициент теплопроводности сухой ткани; W – влагосодержание ткани в % .

Влиянием температуры на λ _вл в пределах до 80 °C в материале можно пренебречь [12].

Эксперимент

Режимы сушки даны в таблице 1.

На рисунке 1 ( а , б ) приведены кривые сушки u = f ( т ) ( а ) и расчетные экспериментальные кривые t_p = f ( τ ) ( б ) для процессов сушки шерстяных тканей для режимов сушки № 1 и № 3 по формулам (9) и (18).

На рисунке 2 даны кривые сушки u = f ( τ ) и температурные кривые t p = f ( т ) для конвективно-терморадиационной сушки вискозной и льняной тканей при различных режимах сушки.

В таблицах 2, 3 и 4 дано сопоставление основных параметров сушки тканей с экспериментальными данными. Погрешность расчётных значений с учётом погрешностей при обработке опытных данных находится в допустимых пределах 5–7%.

Заключение

Представлен метод расчета процесса сушки тканей. Даны необходимые формулы для определения всех основных кинетических характеристик процесса сушки тканей. Дана проверка достоверности полученных уравнений и сопоставление расчетных значений с экспериментальными. Разбежка значений находится в пределах точности проведения и обработки опытных данных.

Таблица 1 – Режимы для конвективной и конвективно-радиационной оценки тканей по кривым оценки представлены на рисунках 1 и 2
Режимы сушки	Конвективная сушка ткани				Конвективно-радиационная оценка ткани
	Шерстяная ткань				Вискозная ткань			Льняная ткань
	1	2	3	4	1	2	3	4	5
u₀	1,1	1,1	1,1	1,1	0,9	0,9	0,9	1,36	1,30
u_p	0,02	0,016	0,018	0,04	0,03	0,02	0,015	0,02	0,02
t c , °C	90	90	87	65	80	100	120	100	120
t èçë , °C	–	–	–	–	150	190	250	190	250
ϑ , м/с	5	2,8	0,9	5,6	1	0,9	0,9	1,1	0,8
φ , %	6	5	5	5	5	5	5	5	4
N_макс , c^-1	0,016	0,0096	0,0073	0,0057	0,0031	0,0048	0,0068	0,0096	0,0176

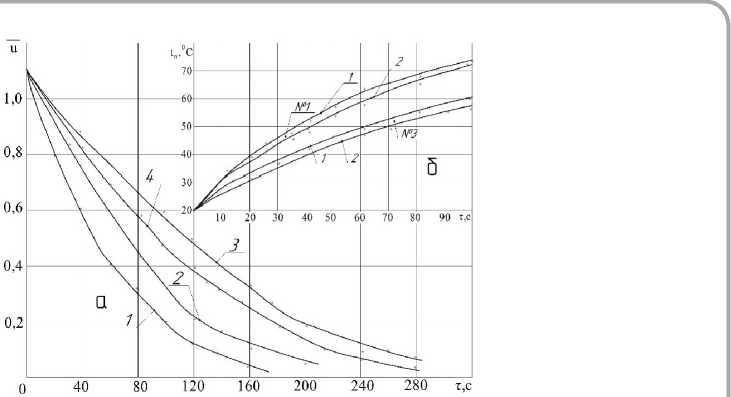
Рисунок 1 - Кривые сушки u = f ( т ) (а) и экспериментальные температурные кривые t p = f ( т ) (б) для конвективной сушки шерстяных тканей. Температурные кривые для режимов № 1 и № 3 по формулам (9) и (18): 1 – по формуле (9), 2 – по (18)

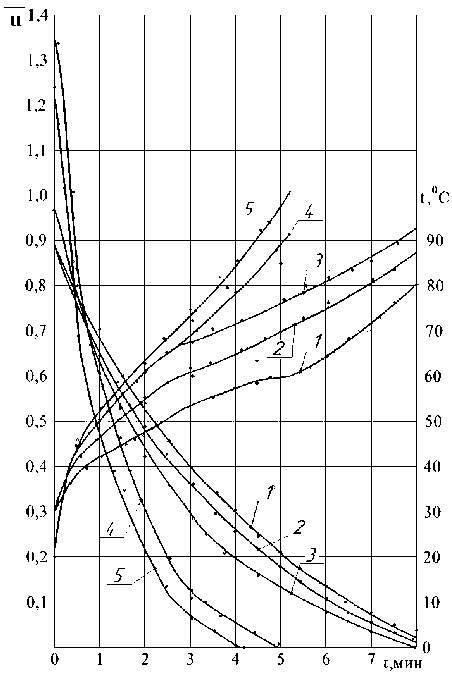
Рисунок 2 - Кривые сушки u = f ( т ) и экспериментальные температурные кривые t p = f ( т ) (указаны в таблице 2)

Таблица 2 – Значения основных параметров кинетики конвективной сушки шерстяных тканей для режимов № 1 и № 3 по формулам (26), (27), (14), (11), (13), (12), (9), (18)
Шерстяная ткань,толщина 8 = 0,440 -3 м ; р ₀ = 200 кг/м³ ; Х ₀ = 0,046 Вт/м • ° C . Режим сушки № 1. t_c = 90 °C ; 9 = 5 м/с ; ф = 5 % ; t_мm = 42 ° C ; U₀ = 1,1; и_р = 0,02; t_H = 20 °C ; N_макс = 0,016 с¹ ; а = 39,6 Втм • C ;^_ с = 1920 Вт/м² ; j ма _KC = 0,840 ³ кг/м² • с
и	α , Вт/м² • °C (26)	λ вл , Вт/м • °C (27)	Bi	q , Вт/м² (14)	q , Вт/м² (11)	q , Вт/м² (13)	j , кг/м² • с (12)	t n . , °C (9)	t n , °C (18)	τ , с (экс)
0,8	34,6	0,238	0,058	1463	1440	1412	0,582	37,2	36,6	20
0,7	32,7	0,216	0,061	1228	1224	1222	0,508	43,6	42,2	35
0,6	30,7	0,199	0,064	1170	1057	1058	0,436	45,5	43,6	40
0,5	28,4	0,169	0,067	923	879	884	0,364	51,2	51,8	51
0,4	25,8	0,146	0,071	689	708	697	0,292	55,2	55,6	60
0,3	22,7	0,125	0,074	496	520	522	0,218	69,8	67,5	83
0,2	19,3	0,086	0,086	298	321	326	0,145	74,6	72,4	98
Шерстяная ткань,толщина 8 = 0,440 -3 м ; р ₀ = 200 кг/м³ ; Х ₀ = 0,046 Вт/м • ° C . Режим сушки № 3. t_c = 87 °C ; 9 = 0,9 м/с ; ф = 6 % ; t_мm = 36 ° C ; U₀ = 1,1; u p = 0,016; t_H = 20 °C ; N_мaкс = 0,0073 с¹ ; а = 19,6 Вт/м² • ° C ; 9_макс = 1152 Вт/м² ; j_макс = 0,4840 -3 кг/м ²-с
и	α , Вт/м² • °C (26)	λ _вл , Вт/м • ° C (27)	Bi	q , Вт/м² (14)	q , Вт/м² (11)	q , Вт/м² (13)	j , кг/м² • с (12)	t n , °C (9)	t n , °C (18)	τ , с (экс)
0,8	17,2	0,237	0,028	778	826	838	0,35	42,7	38,7	50
0,6	16,3	0,211	0,032	596	622	629	0,26	50,5	48,6	92
0,5	14,9	0,172	0,035	458	504	502	0,22	56,2	54,5	120
0,3	12,6	0,126	0,036	286	302	314	0,134	62,0	59,3	160
0,2	10,5	0,081	0,048	187	210	212	0,087	70,2	69,4	200

Таблица 4 – Сопоставление длительности сушки тканей с экспериментальными значениями по формулам (16) и (20)
u	Ткань шерстяная. Режим сушки № 1. ^Nмaкс = ^0,016 С -			Ткань льняная. Режим сушки № 4. ^Nмакс = ^0,011 с -1			Ткань вискозная. Режим сушки № 1. ^Nмакс = ^0,0041 с -
u	T , с (экс)	T , с (16)	T , с (20)	T , с (экс)	T , с (16)	T , с (20)	T , с (экс)	T , с (16)	T , с (20)
0,8	20	20,9	20,7	45	45,5	47,4	36	38,2	36,2
0,6	40	39,6	41,1	72	73,4	72,3	92	89,6	88,7
0,4	60	60,7	63,2	111	115	112,6	182	184,4	180,4
0,2	98	96,4	109,8	190	189	186	310	310,4	313,3

Таблица 3 – Значения основных параметров кинетики конвективно-радиационной сушки льняной и вискозной тканей для режимов № 4 и № 1 по формулам (26), (27), (14), (11), (13), (12), (9), (18)
Ткань льняная, толщина 8 = 0,540 ^-3 м ; р ₀ = 200 кг/м³ ; А ₀ = 0,046 Вт/м • ° C ; с₀ =1560 Дж/кг • ° C . Режим сушки № 4. t_c = 100 °C ; t_a3a = 190 °C ; 8 = 1,1 м/с ; ф = 5 % ; 1_мт = 42 °C ; и₀ = 1,36; u_p = 0,02; t_K = 20 °C ; N_макс = 0,0096 с¹ ; a = 28,7 Вт/м² • °C ; q_макс = 1960 Вт/м² ; j_макс = 0,8240^-3 кг/м² • с
и	α , Вт/м² • °C (26)	^λ вл ^, Вт/м • °C (27)	Bi	q , Вт/м² (14)	q , Вт/м² (11)	q , Вт/м² (13)	j , кг/м² • с (12)	t n , °C (9)	t n , , °C (18)	t n , °C (экс)	τ , с (экс)
1,1	24,5	0,241	0,053	1620	1584	1498	0,65	32	31	34	22
0,8	22,9	0,214	0,057	1310	1288	1143	0,52	42	43	43	45
0,6	20,4	0,185	0,059	1066	978	868	0,43	48	50	48	72
0,4	17,3	0,167	0,060	764	782	677	0,34	57	59	57	111
0,2	12,8	0,125	0,061	442	470	438	0,22	70	66	67	190
0,1	9,8	0,115	0,063	267	276	242	0,13	78	78	76	220
Ткань вискозная,толщина 8 = 0,540^-3 м ; р ₀ = 330 кг/м³ ; А ₀ = 0,058 Вт/м • °C ; с₀ =1610 Дж/кг • °C . Режим сушки № 1. t_c = 80 °C ; t_aM = 150 °C ; 8 = 1 м/с ; ф = 6 % ; 1_мт = 38 °C ; и₀ = 0,9; u p = 0,03; t_K = 20 °C ; N_макс = 0,0031 с^-1 ; a = 18,6 Вт/м² • °C ; q_макс = 880 Вт/м² ; j_макс = 0,3840 —3 кг/м² • с
и	α , Вт/м² • °C (26)	λ вл , Вт/м • °C (27)	Bi	q , Вт/м² (14)	q , Вт/м² (11)	q , Вт/м² (13)	j , кг/м² • с (12)	t n , , °C (9)	t n , °C (18)	tn , °C (экс)	τ , с (экс)
0,7	16,8	0,165	0,060	639	670	675	0,29	38	41	40	56
0,5	14,6	0,136	0,064	500	492	487	0,22	48	51	48	126
0,4	13,3	0,122	0,065	334	379	394	0,17	55	56	57	182
0,2	9,9	0,092	0,066	210	195	210	0,10	64	66	68	310
0,1	7,5	0,075	0,063	100	97	110	0,06	72	73	74	396

res of the drying process of non-woven textile materials [Osobennosti processa sushki netka-nyh tekstil'nyh materialov], Sbornik nauchnyh statej Pervyh Mezhdunarodnyh Lykovskih nauch-nyh chtenij – Collection of scientific articles of the First International Lykov Scientific Readings , 2015, pp. 205–210.

(1971), Sushka pishhevyh rastitel'nyh materialov [Drying of food plant materials], Moscow, 439 p.

Список литературы Новый метод расчета кинетики процесса сушки тканей

Балыхин, М. Г., Разумеев, К. Э., Кошелева, М. К., Захарова, А. А. (2015), Процессы сушки и термовлажностной обработки в текстильной и лёгкой промышленности, Сборник научных статей Первых Международных Лыковских научных чтений, 2015, С. 193–205.
Кошелева, М. К., Рудобашта, С. П. (2015), Особенности процесса сушки нетканых текстильных материалов, Сборник научных статей Первых Международных Лыковских научных чтений, 2015, С. 205–210.
Акулич, П. В. (2010), Расчеты сушильных и теплообменных установок, Минск, 443 с.
Лыков, А. В. (1968), Теория сушки, Москва, 472 с.
Васильев, В. Н., Куцакова, В. Е., Фролов, С. В. (2013), Технология сушки. Основы тепло- и массопереноса, Санкт-Петербург, 224 с.
Ольшанский, А. И., Жерносек, С. В., Ольшанский В. И. (2014), Графоаналитический метод расчета конвективно-терморадиационной сушки технических тканей, Вестник Витебского государственного технологического университета, 2014, № 26, С. 74
Ольшанский, А. И., Жерносек, С. В. (2014), Исследование процесса конвективно-радиационной сушки технических тканей методом регулярного режима, Инженерно-физический журнал, 2014, Т. 87, № 5, С. 1113–1122.
Лыков, А. В. (1972), Тепломассообмен. Справочник, Москва, 557 с.
Лыков, А. В. (1961), Теоретические основы строительной теплофизики, Минск, 519 с.
Филоненко, Г. К., Гришин, М. А., Коссек, В. К. (1971), Сушка пищевых растительных материалов, Москва, 439 с.
Ольшанский, А. И. (2013), Кинетика теплообмена и экспериментальные методы расчета температуры материала в процессе сушки, Инженерно-физический журнал, 2013, Т. 86, № 3, С. 584–594.
Лыков, А. В., Михайлов, Ю. А. (1963), Теория тепло- и массопереноса, Москва, 536 с.
Колесников, П. А. (1965), Теплозащитные свойства одежды, Москва, 345 с.
Григорьев, И. С. (1991), Физические величины. Справочник, Москва, 1232 с.

Еще

Статья научная