Новый подход к анализу свойств неупорядоченных структур в гидродинамической акустике как дополнение в технологию и теорию обнаружения

Цитирование: Стародубцев, П. А. Новый подход к анализу свойств неупорядоченных структур в гидродинамической акустике как дополнение в технологию и теорию обнаружения / П. А. Стародубцев, Е. П. Стародубцев, Р. Н. Алифанов, Г. В. Дорофеев // Журн. Сиб. федер. ун-та. Техника и технологии, 2021, 14(3). С. 306–315. DOI: 10.17516/1999–494X-0310

Научная задача исследований будет связана с процессом аналитического рассмотрения не систем, формирующих гидроакустические сигналы или их принимающие, а среды, в которой распространяются акустические колебания, т. е. воды и ее «неупорядоченных» систем, в которых отсутствует дальний порядок в расположении частиц. При этом к неупорядоченным системам отнесем жидкости, аморфные и стекловидные вещества. Несмотря на отсутствие дальнего порядка, ближний порядок в таких системах может сохраняться.

Основная часть

При проведении научно-исследовательских работ (НИР) в период c 2008 по 2017 г. в заливе Стрелок у северо-восточного берега залива Петра Великого Японского моря (южное побережье Приморского края), в отдельных районах у острова Путятин, лежащего посередине залива и делящего его почти пополам, были обнаружены неупорядоченные системы (вихревые аномалии), обладающие свойствами странных аттракторов, переходящих во фрактальные области. При изменении их пространственных размеров эти аномалии сохраняли свои геометрические и физические свойства самоподобия от итерации к итерации [1] (рис. 1).

По своей структуре залив Стрелок напоминает естественный резонатор, в котором возможно внутреннее переотражение акустических волн, практически без потери энергии.

Динамика формы аттрактора постоянно в различных масштабах монотонно убывала, затем возрастала и проявляла фрактальное самоподобие. Эти факты дали возможность пояснить причины, послужившие основанием для обнаружения звуковых вариаций самого аттрактора и шумового поля движущегося морского объекта без визуального его наблюдения на поверхности, а интеграция аттрактора и его динамики в виде фрактала явилась условием обнаружения акустического поля от объектов естественного и искусственного происхождения в водной среде в условиях материковой отмели и закрытых бухт [1].

Такой же звук наблюдался и фиксировался и от банки Бонсдорфа (банка у бухты Нерпичья, западная часть залива Петра Великого) (рис. 2) и представлял собой шумовой фрактал, по структуре подобный вихревым и турбулентным шумам.

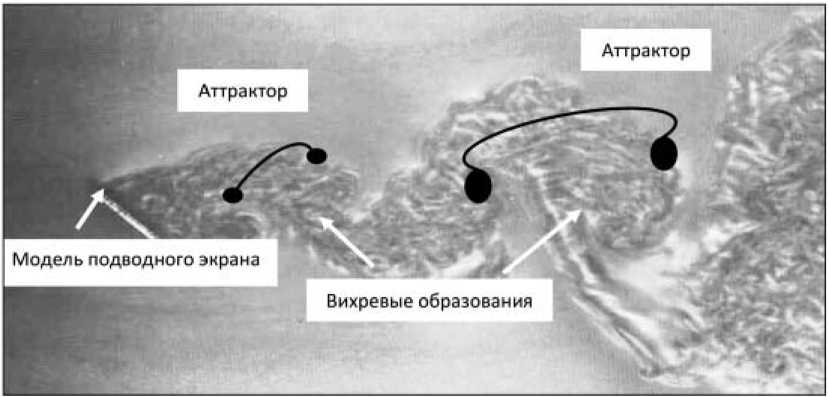
Рис. 1. Странные аттракторы, переходящие во фрактальные области [1]

Fig. 1. Strange attractors turning into fractal regions [1]

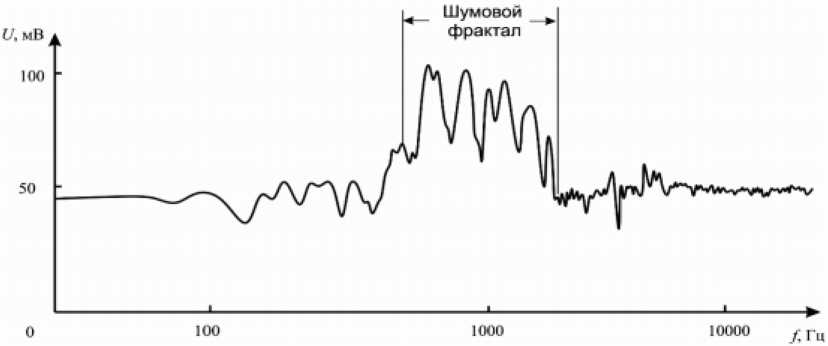
Рис. 2. Шумы от банки Бонсдорфа [1]

Fig. 2. Noises from the Bonsdorf bank [1]

Причиной появления такого физического «самоподобия», по мнению авторов, служит географическая структура залива Стрелок. Он вдается в сушу между мысом Майделя и мысом Гембачева, длина его около 12 км, ширина до 15 км, глубина до 46 м. Берега залива высокие и каменистые. В берега залива вдается несколько бухт, крупнейшие из которых Разбойник, Абрек, Руднева, Чажма, а также бухта Назимова на острове Путятина. Кроме острова Путятина также имеется еще несколько более мелких островков и скал: остров Никольского, камни Унковского, остров Ирецкого, кекуры Пять Пальцев.

Данные научные выводы (частично) в 2014 г. также подтвердили сотрудники [2] Государственного океанографического института им. Н. Н. Зубова и Санкт-Петербургского государственного университета (А. Е. Зверева и В. Р. Фукс). Они выдвинули гипотезу о наличии в Японском море «котловинных» волн. По мнению авторов статьи, свойства «котловинных» волн близки «самоподобным» вихревым потокам в мелководных районах залива Петра Великого (рис. 3).

С точки зрения А. Е. Зверева и В. Р. Фукс [2], есть основания полагать, что в котловине Ул-лын Японского моря происходит топографический захват энергии этих волн. «Котловинные» волны принадлежат классу градиентно-вихревых волн, они обязаны своим происхождением совместному эффекту вращения и сферичности Земли, а также топографическим особенностям акватории. «Котловинные» волны, наряду с шельфовыми, склоновыми и «желобовыми» (двойными волнами Кельвина), можно также отнести к классу топографических волн Россби.

Для выяснения особенностей динамики топографических волн [2] были подготовлены массивы альтиметрических данных с 1992 по 2013 г. и оценены статистические характеристики изменчивости альтиметрического рельефа поверхности моря при различных масштабах пространственно-временного осреднения. Подтвердилось предположение о доминировании стояче-поступательных волн, что позволяет объяснить многие ранее не объяснявшиеся явления в Японском море, такие как скачкообразное изменение фазы при перемещении неоднородностей в поле уровня, ячеистая структура возмущений уровня и течений с выраженными амфидромиями в центрах этих ячеек [2].

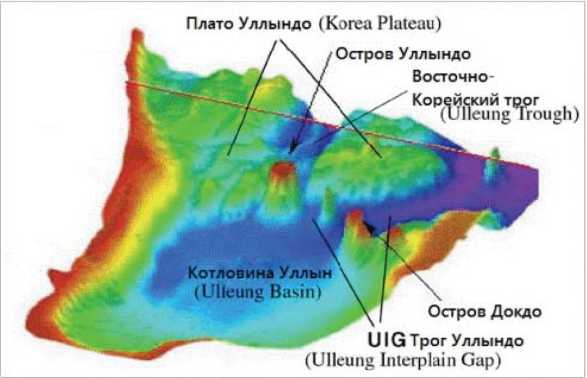
Рис. 3. Донная топография котловины Уллын (Японское море) [2]

Fig. 3. Bottom topography of the Ulleung Basin (Sea of Japan) [2]

Было отмечено, что увеличение кинетической энергии колебаний в котловине свидетельствует о том, что существует физический механизм, аккумулирующий эту энергию в котловине [2].

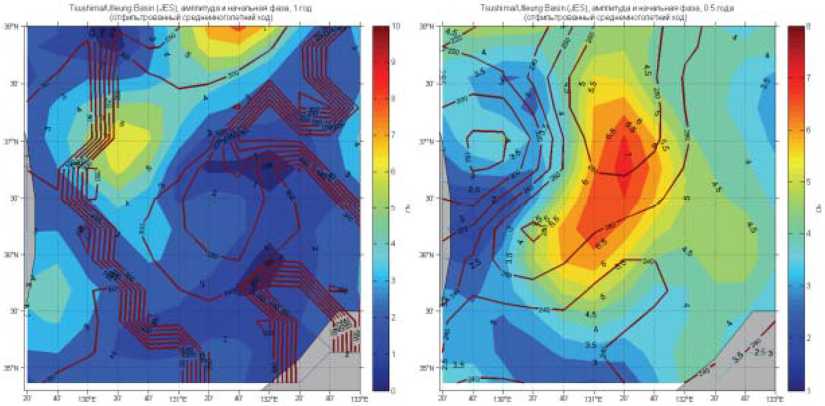
В пространственных распределениях амплитуд и начальных фаз четко выделяются области с пониженными значениями амплитуд и существенным сгущением линий изофаз (рис. 4). Согласно кинематике стоячих и стоячепоступательных волн в теории приливов данные области являются амфидромическими. Годовой период отличается повышенной амплитудой уровня моря в области теплого вихря Уллын на северо-западе области с относительно низкими значениями на юго-востоке, где отмечается холодный вихрь Док. Эти две зоны окружены кольцевыми котидальными линиями. Полугодовой период имеет обратную картину распределения максимумов: положительная аномалия амплитуды находится юго-восточнее отрицательной [2] (рис. 4).

Логика анализа представленных выше данных [1, 2] привела к выводу, что самоподобие (как физическое явление) должно отмечаться и в других условиях. Достаточно «сложное» для полного объяснения влияние на структуру и характер акустического поля среды (например, в бухте Стрелок залива Петра Великого) оказывают сейши. Как показали исследования [3], в данном районе они представляют собой [3] стоячие свободные колебания жидкости в «полузамкнутом» пространстве (рис. 5) с формированием одноузловой структуры.

Если упомянутые выше неупорядоченные системы возникают [1–3] в результате сложных взаимодействий сил природы (апвелинги, сейши, силы Кориолиса, течения, конвекционные потоки, вращение Земли) и являются по своей сути механическими воздействиями на среду формирования и распространения акустического поля, то механические источники звука, внесенные в гидросферу (в воду), должны в более мелких масштабах повторять на уровне звукового поля фрактальные итерации.

Решение научной задачи

Нужно только знать, какими размерами колеблющихся частиц следует оперировать в этом случае. Что значит выражение: «В гидродинамике среда считается сплошной и рассматрива- – 310 –

а)

б)

Рис. 4. Карты амплитуд и начальных фаз аномалий уровня для годового (а) и полугодового (б) периода [2]

Fig. 4. Maps of amplitudes and initial phases of level anomalies for annual (a) and semi-annual (б) periods [2]

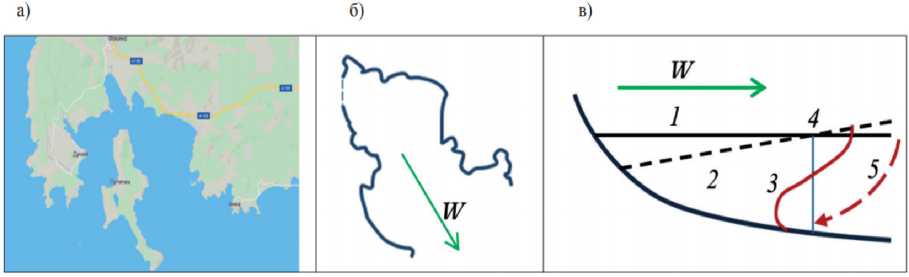
Рис. 5. Формирование одноузловой сейши: а – акватория залива Петра Великого; б – направление нагонного ветра; в – последовательность появления одноузловой сейши [3]

Fig. 5. Formation of a one-node seiche: a – water area of the Peter the Great Bay; б – the direction of the surge wind; в – the sequence of the appearance of a single-node seiche [3]

емый в ней объем среды мал в сравнении с размерами макроскопических тел, но достаточно велик по сравнению с расстоянием между молекулами» [4–5]? Это сколько?

Если мы беремся решать задачу обнаружения акустически малозаметных объектов, то прежде всего необходимо пересмотреть в теории гидроакустики целый ряд положений, содержащих ранее принятые допущения и линеаризации. Проанализировать их справедливость на этапе более высокого уровня математического аппарата обработки потоков информации вообще и акустических исследований в частности. Согласиться с тем, что теория гидроакустического поля имеет свои совершенно специфические особенности, не дающие возможность использовать аппарат исследования, пригодный для исследования газов и твердых тел.

Нельзя полностью переносить теорию волновых процессов в атмосфере на волновые процессы в морской среде. Примером может служить изотопный фактор строения воды. Физический энциклопедический словарь [6] трактует, что вследствие существования 3 изотопов водо- рода - протия, дейтерия и трития - и 6 изотопов кислорода - O14, O15, O16, O17, O18, O19 имеется 36 изотопных разновидностей воды.

Если признать основополагающими уравнениями гидроакустики уравнения гидродинамики (уравнение движения, уравнение непрерывности и уравнение состояния), нелинейность этих уравнений вынуждает считать теорию гидроакустического поля нелинейной, а линейность процессов в этом исследовании – частным случаем.

Признание этого фактора требует пересмотра некоторых позиций, о которых будет сказано ниже. Сейчас отметим только то, что принцип суперпозицим становится также частным случаем, а преобразование Фурье, оставшись необходимым, теряет свою достаточность. К нему в помощь должен быть привлечен фрактальный анализ в сочетании с вейвлет-анализом. Это, в свою очередь, неизбежно приведет к пространственному разложению функции, т. е. к тензорному аппарату вычислений [7].

Концептуальный пересмотр теории акустического поля

Это должно стать концептуальным пересмотром теории акустического поля для условий обнаружения акустически малозаметных объектов.

Акустические процессы в водной среде относятся к процессам, в которых микроскопические связи между частицами среды определяют макроскопическое поведение всей среды.

Природа устроена таким образом, что микроскопическая структура многих неупорядоченных объектов обладает свойством масштабной инвариантности (скейлинга). Масштабная инвариантность позволяет строить теорию таких сред с помощью методов ренормализацион-ной группы (также часто называемый методом ренормгруппы, методом РГ).

В квантовой теории поля это итеративный метод перенормировки, в котором переход от областей с меньшей энергией к областям с большей вызван изменением масштаба рассмотрения системы.

Модель нетривиальной масштабно-инвариантной структуры

Этот подход универсален, но связан с объемными вычислительными процессами, которые еще десять лет назад были трудно осуществимы. Развитое Мандельбротом математическое понятие фрактала (по Мандельброту, изломанный объект с дробной размерностью) и его приложения к описанию форм различных объектов дают возможность составить модель нетривиальной масштабно-инвариантной структуры, похожей на кластерную сруктуру «слияния» частиц водной среды [8, 9].

Новый подход к анализу неупорядоченных структур в гидродинамической акустике

В применении такой модели заключается новый подход к анализу неупорядоченных структур в гидродинамической акустике. Фрактальные модели не всегда поддаются аналитическому исследованию, но могут быть построены по простым правилам с возможностью несложной компьютерной реализации. С помощью языка программирования императивного типа со строгой статической типизацией переменных «Delphi» можно строить фракталы – 312 – самых разнообразных форм. Закономерности сложных неупорядоченных процессов изучают в компьютерных экспериментах с подобными моделями.

Такой подход значительно отличается от традиционных методов теоретической физики (например, выбор точек обработки информации при анализе сигнала по уравнению Бине и его частному случаю – числу Фибаноччи). Это отличие не сводится к разнице между численным решением дифференциальных уравнений и их аналитическим исследованием.

Фракталы как нелинейные процессы

Фракталы позволяют продвинуться в исследовании акустических процессов как нелинейных процессов. Причем под нелинейностью понимается не частный случай, обусловленный энергетическими всплесками, а нормальное состояние среды, в которой формируется и распространяется акустическое поле, среды, в которой линейные процессы являются идеализированными случаями теоретического плана.

Все акустические процессы в водной среде должны изначально приниматься к рассмотрению с позиций нелинейности. Должны рассматриваться условия согласованности источника колебаний в водной среде со свойствами самой водной среды.

Поясним это примером. Принимаем, что однородная водная среда имеет постоянный коэффициент упругости k упр , благодаря которому при восстановлении состояния среды после адиабатического сжатия возврат частиц в исходное состояние происходит со скоростью v _упр.

Источник звуковых волн, внесенный в водную среду, вибрирует с такой частотой, что вынуждает вибрирующие частицы двигаться со скоростью v _виб. Если скорость вынужденного движения равна собственной скорости движения частиц воды за счет собственных свойств среды, обусловленных упругими ее свойствами, т. е. имеет место равенство

• ^v упр ^v виб ,

то можно говорить о линейности процессов, происходящих в среде.

При уменьшении частоты колебаний источника наступает фаза неравенства скоростей типа v _упр >  v _виб. В этом случае частицы воды будут обгонять частицы поверхности излучателя, искажать гармоничность колебательного процесса и создавать дополнительные напряжения между излучающей поверхностью и водной средой, которые приводят к «измельчению» кластерной структуры водной среды в зоне колебания.

При увеличении частоты колебаний источника наступает фаза типа v _упр<  v _виб. В этом случае частицы воды будут отставать от частиц поверхности излучателя, искажая гармоничность колебания среды, и создавать «пустоты» в среде, неизбежное сжатие которых вызывает микровзрывы и разрушение кластерной структуры воды.

Время восстановления кластерной структуры водной среды для v _упр >  v _виб и v _упр<  v _виб случаев неравенства скоростей будет определяться в общем случае различными алгоритмами. Время восстановления кластерной структуры будет иметь разную величину.

Заключение

В итоге если время восстановления кластерной структуры воды составляет tвост, то за промежуток времени от 0 до tвост можно обнаружить нарушение кластерности воды и классифици- ровать по частоте источник излучения (частота излучения выше собственных колебаний среды или ниже). Дополнительную окраску классификационных признаков источников колебаний дает смачиваемость вибрирующей поверхности, приводящей к дополнительному искажению гармоничности его колебания. Становится классификационным признаком обрастание биологическими организмами вибрирующих поверхностей. Аномально высокая теплоемкость воды обеспечивается многочисленными водородными связями (механизм Гротгуса). Одна молекула может образовать до четырех классических водородных связей с соседями (с учетом H-связей до 5–6). Водородные связи повышают температуру кипения, вязкость и поверхностное натяжение жидкости, они ответственны за многие другие уникальные свойства воды. Фрактальность водной среды определяется соленостью, температурой, плотностью и давлением. Исследование фрактальности воды неизбежно повлечет за собой изменение содержания эмпирических формул расчета скорости звука в воде.

Представленные в работе выводы могут быть реализованы новой технологией системы регистрации акустически слабозаметных объектов по первичным признакам гидродинамических характеристик среды и шумовых полей объектов с использованием приборов и устройств векторного анализа и синтеза.